正弦量的相量表示

格式：ppt
大小：1.22 MB
文档页数：8

下载文档原格式

正弦量的相量表示

消去式中各项的公因子，则有
j LI m RI m U sm
由此解出
U sm Im R jL
U sm R 2 ω 2 L2 e
ωL jψu arctan R
稳态响应电流为
i ( t ) Im I me j t
U sm
U Uψu
幅值相量与有效值相量的关系
有效值相量
Um
U m U m ψu
2Uψu 2U
相量图 (phasor diagram)
U
ψu
+1
在复平面上用以表示正弦量的矢量图，称为相量图。
正弦量与相量的关系：
Im
u( t ) Im U me jψu e jω t

ωL sinω t ψu arctan 2 2 2 R R ω L
由此看出，用相量表示正弦量后可以将电路的微分方程转化为复数代数方程，从而使计算得以简化。能否直接由电路图写出复数的代数方程呢？要做到这一步还必须介绍基尔霍夫定律的相量形式和电路元件方程的相量形式。
下面举例说明例求图示电路的正弦稳态响应电流i (t)。激励函数
解：
us ( t ) U sm sin( t ψu ) Im U sme jω t ω
设正弦稳态响应电流
பைடு நூலகம்

i ( t ) I m sin( t ψi ) Im[ I me jωt ] ω
电路的微分方程为
di ( t ) L Ri( t ) us ( t ) dt
代入i(t)和us(t)，可得
Im[j LI me j t RI me j t ] Im[U sme j t ]

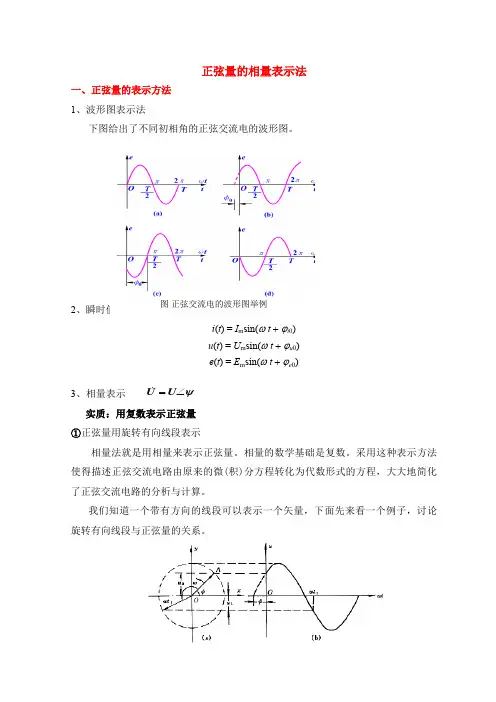
2.2正弦量的相量表示法

正弦量的相量表示法一、正弦量的表示方法1、波形图表示法下图给出了不同初相角的正弦交流电的波形图。

2、瞬时值表达式 i (t ) = I m sin(ω t + ϕi 0)u (t ) = U m sin(ω t + ϕu 0)e (t ) = E m sin(ω t + ϕe 0)3、相量表示实质：用复数表示正弦量①正弦量用旋转有向线段表示相量法就是用相量来表示正弦量。

相量的数学基础是复数。

采用这种表示方法使得描述正弦交流电路由原来的微(积)分方程转化为代数形式的方程，大大地简化了正弦交流电路的分析与计算。

我们知道一个带有方向的线段可以表示一个矢量，下面先来看一个例子，讨论旋转有向线段与正弦量的关系。

图正弦交流电的波形图举例 ψU U ∠=设正弦量U= U m sin(ωt +ψ)若: 有向线段长度 = Um有向线段与横轴夹角 = 初相位ψ有向线段以速度ω按逆时针方向旋转则:该旋转有向线段每一瞬时在纵轴上的投影即表示相应时刻正弦量的瞬时值。

例如：在t =t 0时，U 0=U m sin(ωt 0+ψ)在t=t l 时，U 1=U m sin ；(ωt 1+ψ)正弦量可用有向线段表示，而有向线段又可用复数表示，所以正弦量可用复数来表示。

② 复数的几种表示形式在一个直角坐标系中，设：横轴为实轴，单位用+1表示；纵轴为虚轴，单位用+j 表示，则构成复数平面(又称复平面)。

图所示的有向线段A ，其复数表示式为：a ．代数式 A=α+ jba=rcosψ ，b=rsinψb ．三角式根据欧拉公式：c ．指数式 A= re j ψd ．极坐标式一个复数可用代数式、三角式、指数式和极坐标式四种表示形式，四者可以互相 ψr A =ψψψsin j cos e j +=可得:ab ψarctan =22b a r +=复数的模复数的辐角 )sin j (cos sin j cos ψψr ψr ψr A +=+=,e e 2cos j j ψψψ-+=2j sin j j ψψψ--=e e转换。

正弦量的相量表示法

小结:
❖ 正弦量能够用相量表达，正弦量也能够用复数表达。
❖ 正弦量旳相量旳幅角等于正弦量旳初相角，相量旳模等于正弦量旳最大值或有效值。
❖ 为了使计算成果能直接表达正弦量旳有效值，一般使相量旳模等于正弦量旳有效值，即能够表达为： U Ue j U
❖ 将几种同频率旳正弦量用相应旳相量表达并画在同一种坐标平面上，这么旳图叫做相量图。
❖ 在同一量图中，以t＝0时刻旳相量表达正弦量。
作业：
❖ 课后复习本节内容。 ❖ 预习下一节“交流电路基本元件”。
谢谢,再见!
2023年9月
（ 4 ）正弦量旳瞬时值＝相量虚部
u U
例1：已知 i1 10 2sin t 30A
+j
试i2 写 5出I21s和inI2旳t 体 6现0式A，并
画出其向量图。
I1 解: i1 和 i2 相应旳电流向量
30
体现式分别为
0 -60
+1
I1 1030 A
I2
I2 5 60A
I1旳长度是I2旳二倍。
例2：
已知 A1 10 j5，A2 3 j4
求
A1 A2 和
A1 A2
。
解: A1 10 j5 11.1826.57
A2 3 j4 553.13
A1 A2 11.1826.57 553.13
55.9079.70
A1 A2
11.1826.57 553.13
2.236 26.56
这么，表达正弦电压 u Umsin t
旳相量为
U m Ume j Um
为了使计算成果能直接表达正弦量旳有效值，一般使相量旳模等于正弦量旳有效值，即能够表达为：

正弦量的相量表示及运算

蒸发操作的类型
1. 按二次蒸气的利用情况分：单效蒸发和多效蒸发
单效蒸发：将二次蒸气不在利用而直接送到冷凝器冷凝以除去的蒸发操作。多效蒸发：若将二次蒸气通到另一压力较低的蒸发器作为加热蒸气，则可提高加热蒸气（生蒸气）的利用率，这种串联蒸发操作称为多效蒸发。
一、正弦量的相量表示
1. 复数的表示形式用相量来表示相对应的正弦量的方法称为相量表示法。相量本身就是复数。一个复数可用下面4种形式来表示：设A为复数 (1) 代数式A =a + jb
式中:
r a2 b2
arctan b
a
a r cos
复数的模复数的辐角
b r sin
一、正弦量的相量表示
一、正弦量的相量表示
2．复数的四则运算设有两个复数分别为：A1 r1a a1 jb1 A2 r2b a2 jb2
A1、A2加、减、乘、除时运算公式如下： A1 A2 (a1 a2 ) j(b1 b2 )
A1 A2 (a1 a2 ) j(b1 b2 )
A1 • A2 r1r2a b
A1 A2 1030 845 (10cos30 10 j sin 30) (8cos45 8 j sin 45) (8.66 j5) (5.656 j5.656) 3.004 j0.6156A
A1 A2 1030845 108(30 45) 8075A
A1 1030 10 (30 45) 1.25 15A A2 845 8
A1 A2
r1 r2
a
b
显然，复数相加、减时用代数形式比较方便；复数相
乘、除时用极坐标形式比较方便。
一、正弦量的相量表示
例题：有两个复数分别为A1 1030，A2 845 试分别对它们做加、减、乘、除运算。

《电工电子技术》课件——正弦量的相量表示法

正弦量用相量表示
同频率正弦量相加——平行四边形法则
由勾股定理得： U
UR2
U
2 L
因。UR IR UL IXL
U
(IR)2 (IX L)2 I
R2
X
2 L
arct an
XL R
正弦量用相量表示
串联电路电流相等。假设i Im sin t
电阻两端的电压：
uR Ri I m R sin t U m sin t
m
sin(t
2
)
电路两端的总电压：u uR uL
正弦量如何进行求和运算？
相量法
正弦量用相量表示
1. 描述正弦量的有向线段称为相量。若其长度用最大值表示，则用
•
•
符号：Um Im ，称为最大值相量。
2. 在实际应用中，长度更多采用有效值，则用符号：U•
•
I
称为有效值相量。
表示，
正弦量用相量表示
相量的复数表示
将相量U• 放到复平面上，如表所示：相量前端点所对应的复数可以表示这个相量。
相量的复数表示
该相量长度 U 称为复数的模，模总是取正值。相量的模 = 正弦量的有效值。
该相量与实轴正方向的夹角称为复数的辐角。相量辐角 = 正弦
量的初相角。
相量的复数表示
•
U a jb
U (cos j sin )
正弦量的相量表示法
引入
电感线圈是由导线绕成的，导线有一定的直流电阻。因此，实际电感可等效成一个理想电感与电阻串联。
引入串联电路电流相等。假设i Im sin t
，则：
电阻两端的电压：
uR Ri I m R sin t U m sin t

正弦量的相量表示

4.相量图
只有同频率的相量才能在同一复平面内作相量图
例1.指出下列各表达式那些是正确的，那些是错误的。
1) i 5 sin(t 30 ) 5e
j 30
2) I 1030
10045 100 2 sin(t 45 ) 3) U
4)
20 I 20e
5 I 2 4 6
1)
I 1 4 6
2)
i1 4 2 sin( 314t

6
)
5 i 2 4 2 sin( 314t ) 6
例4.写出电流
i1 ( t ) 5 sin(t 45 ) A, i2 ( t ) 10 2 sin(t 120 ) A
iu 1, i
角频率有效值初相位

I1 o
i1
i2
i 2 I2
i1+i2 i3

I t
3
i3
1
2
3
结论同频的正弦量相加仍得到同频的正弦量，
所以，只需确定初相位和有效值。因此采用正弦量复数变换的思想
3. 正弦量的相量表示
造一个复函数
j( t Ψ )
无物理意义
A(t ) 2 Ie 2 Icos(t Ψ ) j 2 Isin( t Ψ )
的相量形式，求解i1(t)+i2(t)。 5 I 10 120 A I 45 A 解： 2 1 2
5 I1 I 2 45 10120 2 5 (cos 45 j sin 45 ) 10(cos 120 j sin 120 ) 2 5 2 1 5 2 3 ( 10 ) j ( 10 ) 2 2 2 2 2 2 2.5 j 6.16 6.65112.1 A

正弦量的相量表示

正弦量的相量表示————————————————————————————————作者：————————————————————————————————日期：正弦量的相量表示根据欧拉公式，复指数函数可见其虚部和实部都是正弦量，所以一个正弦量就可以表示为与之对应的复指数函数的虚部。

例如一个正弦电流就可以表示为观察式（4-11）的最后一个表达式可发现，该表达式中含有这一因子，而这一因子正是一个相量（复数）的极坐标的表达式，其中I为相量的模，为相量的辐角。

考虑到I和又分别是正弦量的有效值和初相，所以定义：以正弦量的有效值为模，初相为辐角构成的复数就称为该正弦量的有效值相量。

即对于任意一个正弦量，都能找到一个与之相对应的复数，由于这个复数与一个正弦量相对应，把这个复数称作相量。

在大写字母上加一个点来表示正弦量的相量，有效值相量符号分别为、。

设某一正弦电压，则该正弦量的有效值相量为当然，也可以用正弦量的最大值为模，初相为辐角构建出正弦量的最大值相量，如电流、电压，最大值相量符号为、，即作为一个复数，相量也可以在复平面上用有向线段表示，相量在复平面上的图示称为相量图。

如下图所示。

图中相量和是表示同频率正弦量的相量。

例题4-4试用相量表示，，并绘出相量图。

解：温馨提示：相量用大写字母上面加一点来表示、、，以便和普通复数相区别。

但相量运算和普通的复数一样，同样遵守普通复数的加、减、乘、除的运算规则。

相量和普通的复数一样也可以在复平面上用一有向的线段（即相量）来表示，表示这种相量的图称为相量图；只有正弦量才能用相量表示，非正弦量不能用相量表示。

相量只是表示正弦量，而不等于正弦量，它是分析和计算交流电路的一种方法；相量的两种表示形式：相量式、相量图；只有表示同频率正弦量的相量才能画在同一相量图上（可以不画坐标轴，参考相量画在水平方向）。

电路3-2正弦量的向量表示法

u的相量为
U U1 U 2 4 j 4 3 3 3 j3 9.2 j3.9 1023.10 V

所以
u 10 2 sin(t 23.10 )V
电
路
3．2 正弦量的相量表示法
一、相量的概念 I 只反映正弦量的两个要素，而隐含着第三个要素的一个旋转矢量叫做相量。用大写字母上方加一个点来表示。如表示电流的有效值相量。而 U 和 U 则表示电压的有效值相量和最大值相量。

m
电
路
对正弦量
u=Umsin(ωt+Ψ)
最大值相量
对应的相量为

电
路
例3.2.3 u1= 8sin（ωt+60°）V ， u2= 6sin （ωt-30°）V ，试用相量法求电压u=u1+u2 。解：u1的相量为
U1 8600 8cos 600 j8sin 600 4 j4 3 V
u2的相量为

U 2 6 300 6cos(300 ) j 6sin(300 ) 3 3 j3 V
U m U m
U U

电
路
如果
I m 10300
i=10sin(ωt+30°)

则它表示的正弦量为
二、相量图为了计算的方便，经常用图形来表示相量，只有同频率的正弦量其相量才能画在同一复平面上，画在同一复平面上的表示相量的图称为相量图。。
电
下图就是的相量图
路
I m 1030

5-3 正弦量的相量表示法

i ( t ) I m sin( t i )
或
I m I m e j i I m i
I Ie j i I i
相量
U m U m e j u
U U u
正弦量
u( t ) Im(U m e j t ) u( t ) Im( 2Ue j t ) i ( t ) Im( I m e j t ) i ( t ) Im( 2 Ie j t )
20e 20 4)I
例2.根据已知正弦量写出对应相量

2 3 2)u2 20 sin(t ) 4
20 3 2) U 2 4 2
1)u1 10 2 sin(t 10 1)U 1 2
)
例3.根据已知相量写出对应正弦量，频率为工频。
1.复数
A a 2 b2
b arctg a
A a jb
a A cos b A sin
A A(cos j sin )
A Ae j A
e j cos j sin
（欧拉公式）
2.复数运算
A1 A1e j 1 A1 1 a1 jb1
U m U m e j
U Ue j
幅值相量与有效值相量的关系： U m 2U
常用相量表示形式：
U Ue j 指数形式
U U极坐标形式 U U (cos j sin ) 直角坐标形式
同理有：
I Ie j I I (cos j sin )
1)I 1 2 i1 4 2 sin( 314t
2)I 2 2 3 j 2

电工基础049.第49课时.正弦量的相量表示

A
复数
4 2 sin (ω t 30 )A ？
瞬时值，与相量不是相等关系
有效值，表示相量要带圆点
10 60 A 2、已知 I
45 Um 220 e V？
4.已知
100 15V U
i 10 sin ( ω t 60 )A ？最大值，应该是10 2
(cos 30 j sin 30 )

e
j 30

所以：
i sin(t 30 ) sin(t 150 )
3、 = 2–1=90° 如： i1 =3sin(ωt +30°) i2 =4sin(ωt +120°)
正交
(1)用相量图叠加 Im 求和 Im2

4、正弦量相减如：i1=3sin(ωt + 30°) i2=4sin(ωt + 120°) 求：i= i1–i2=? 解： i= i1 +(–i2)，得： Im= 32+42 =5 θ=arctan (I2/I1)=53° 对i1和(–i2)求和，
(1)用相量图叠加
Im2
Im1
1 θ
Im
3）复数j的实部为0，虚部为 1，其极坐标式为 j=1∠90°； 4）复数-j的实部为0，虚部为-1，其极坐标式为 –j =1∠-90°。
19 0
1180
10
0
1 －90
27
＋1
一般情况下，复数的加减运算应把复数写成代数式。
一般情况下，复数的乘除运算应把复数写成较为简便的极坐标式。
（5）相量的书写方式
、模用最大值表示，则用符号： U I m m

3.2 正弦量的相量表示法

所以：i sin(t 30 ) sin(t 150 )
3、 = 2–1=90°正交
(1)用相量图叠加
如： i1 =3sin(ωt +30°) i2 =4sin(ωt +120°)
求和
则： Im= Im12 + Im22 = 5
θ =arctan(对边/邻边) = 53°
(本例）=1+θ =83° i=5sin(ωt+83°)
现有复数A =|A| e j
相量图
A
+1
若令：A• j =|A| e j ·e j 90° 则有：A• j = |A|e j ( + 90°)
由此知，A j使A逆时针旋转90°
相量图 Aj
90°
A
同理， A（- j）使A顺时针旋转90° 故：复平面中，j 是旋转90°的算子符。
+1
接3.3
4.复数的极坐标形式 A = A
复数的四种表示形式，是相量表示法的基础。
3.2.2 正弦量的相量表示法 +j
一、正弦量的相量表示法
b(t)
若，令复数A绕原点，以ω的角速度、逆时针方向旋转，
A
ω
A ωt
+1
则，任何时刻(t)，其虚部的表达式为：
b(t)=|A|sin(ωt +)
形式完全相同
i(t)=Imsin(ωt +)
但当由相量式写解析式时，必须将频率写入。
三、相量表示法举例例1. i=5 2 sin(ωt+30 °) 极大值相量式： Im=5 2∠30° 有效值相量式： I =5∠30°
相量图
5 Iω
30°
+1

正弦量的相量表示

b| A| sinθ
图解法
复数运算
Im
(1)加减运算——采用代数形式
A2
若 A1=a1+jb1， A2=a2+jb2
0
则 A1±A2=(a1±a2)+j(b1±b2)
A1 Re
(2) 乘除运算——采用极坐标形式
若 A1=|A1| 1 ，A2=|A2| 2
则: A 1A 2A 1ej1A 2ej2A 1A 2ej(12)
等于初相位之差
规定： |j | (180°)。
• j >0， u超前ij 角，或i 落后u j 角(u 比i先到达最大值)；
u, i u i
O
wt
yuyi
j
• j <0， i 超前 uj 角，或u 滞后 i j 角,i 比 u 先到达最大值。
特殊相位关系：
j = (180o ) ，反相：
j ＝ 0，同相：
u (t)u 1(t)u 2(t)R e( 2U •1ejwt)R e( 2U •2ejwt)
R e( 2U •1ejwt2U •2ejwt)R e( 2(U •1U •2)ejwt)
可得其相量关系为： U U 1U 2 U
故同频正弦量相加减运算变成对应相量的相加减运算。
i1 i2 = i3
也可借助相量图计算
Im U2
U
U1
41.9
30 60
Re
首尾相接
U
Im
U2
U1
60
41.9
30
Re
2 . 正弦量的微分，积分运算
wy y i 2 I co t s i) (I I i
微分运算:
di d Re 2 Ie jw t

正弦量的相量表示法

正弦量的相量表示法在物理学中，正弦量（sine wave）是一种振荡量，它可以以普遍的正弦函数的形式来表示。

它往往用来表示物理或数学模型中的规律性或周期性变化，因此拥有在物理研究中重要的应用价值。

正弦量也是数字信号处理、生物科技、通信和声学中的重要组成部分。

正弦量的相量（phasor）表示法是对正弦量的一种数学表示方式，用一个复数来表示整个正弦波的大小和相位（即时间延迟）。

正弦量的复数表示法可以将其分解成两个部分，一部分用有理解题目中提到的正弦量的大小（模）来表示，另一部分用相应的正弦量的角度（相角）来表示。

弦量的相量表示法可以用工程学中常见的极坐标和/或复平面形式来表示，可以用曲线图和/或数字示意来表示。

正弦量的相量表示法的基本原理是用一个复数来表示正弦量的实部和虚部，采用极坐标和/或复平面形式来表示。

在极坐标中，我们可以用极径（r）和极角（θ）来表示正弦量：在极坐标中，极径表示正弦量的大小，而极角表示正弦量的相位。

在复平面上，我们可以采用复数的形式来表示正弦量，即复数z的实部和虚部：在复平面上，复数的实部表示正弦量的大小，而复数的虚部表示正弦量的角度。

正弦量的相量表示法有几个优点。

首先，正弦量的相量表示法可以用数字的形式来精确地表示正弦量的相位。

其次，正弦量的相量表示法可以用复数的形式来精确表示正弦量的大小。

最后，正弦量的相量表示法使得正弦量的数学操作变得简单、高效。

正弦量的相量表示法在很多情况下都有重要的应用价值。

例如，在电机控制中，正弦量的相量表示法可以用来描述电机的运动，以及与其相关的特性，如频率、相位和相应的电压、功率等。

此外，正弦量的相量表示法在电子学的元件分析和模拟中也有广泛的应用价值。

由于正弦量的相量表示法的众多优点，在现今的工程学研究中，它得到了越来越广泛的应用。

正弦量的相量表示法为物理学、数字信号处理、生物科技、通信和声学等领域的研究提供了一种新的模型来建立物理模型和模拟信号运行行为，从而改善现有系统的性能。

电路分析基础：正弦量的相量表示法

A=a+jb
A=|A|ej =|A|
直角坐标表示极坐标表示
Im
b
A
|A|
0
a Re
| A |
a2 b2
θ arctg b
a
或
a | A | cosθ
b | A | sinθ
图解法
复数运算
Im
(1)加减运算——采用代数形式
A2
若 A1=a1+jb1， A2=a2+jb2
0
则 A1±A2=(a1±a2)+j(b1±b2)
| A1 | ej(θ1θ 2 ) | A2 |
| A1 | | A2 |
θ125 ?
解 547 10 25 (3.41 j3.657) (9.063 j4.226)
12.47 j0.569 12.48 2.61
例2. 220 35 (17 j9) (4 j6) ?
20 j5
解
原式 180.2
j126.2
19.2427.9 7.21156.3 20.6214.04
180.2 j126.2 6.72870.16
180.2 j126.2 2.238 j6.329 182.5 j132.5 225.536
Im
(t i )
正弦量
复数
3. 复数及运算
A=a+jb
复数A的表示形式
Im
b
A
0
a Re
A a jb
(j 1 为虚数单位)
Im
b
A
|A|
0
a Re
A | A | e j
A | A | e j | A | (cos j sin ) a jb

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例1
已知
解
100 30o A I 220 - 60o V U
上页下页
i 141.4 cos(314t 30o )A u 311.1cos(314t - 60o )V
试用相量表示i, u .
例2
5015 A, f 50Hz . 已知 I
试写出电流的瞬时值表达式。
y -

3
i ( t ) 100 cos(10 t 3
3

3
) t1＝
当 10 t1 3 有最大值
3
10
3
＝1.047ms
上页下页
3. 同频率正弦量的相位差 (phase difference)
设：u(t ) U mcos(t y u ) , i (t ) I m cos(t y i ) 则相位差：j ui (t y u ) - (t y i ) y u -y i
正弦电流电路
激励和响应均为正弦量的电路（正弦稳态电路）称为正弦电路或交流电路。
研究正弦电路的意义（1）正弦稳态电路在电力系统和电子技术领域占有十分重要的地位。优点 1）正弦函数是周期函数，其加、减、求导、积分运算后仍是同频率的正弦函数； 2）正弦信号容易产生、传送和使用。
上页下页
若激励是正弦量，则电路的响应也是同频率的正弦量，正弦量的各阶微分和积分仍然是同频率的正弦量。所以，我们只需关心电路响应的有效值和初相位，可以不理睬正弦量的角频率。
上页
下页
两个正弦量的相加：如KCL、KVL方程运算。
i1 2 I1 cos( t y 1 )
i2 2 I 2 cos( t y 2 )
同理，可得正弦电压有效值与最大值的关系：
1 U Um 2
或
U m 2U
若一交流电压有效值为U=220V，则其最大值为Um 311V； U=380V， Um 537V。
注（1）工程上说的正弦电压、电流一般指有效值，如设备铭
牌额定值、电网的电压等级等。但绝缘水平、耐压值指的是最大值。因此，在考虑电器设备的耐压水平时应按最大值考虑。
周期电流、电压有效值 (effective value) 定义
直流 I
R
交流 i
R
W RI T
2
W Ri ( t )dt
2 0
T
电流有效值定义为
1 T 2 I i (t )dt T 0
def
有效值也称均方根值 (root-mean-square)
上页下页
同样，可定义电压有效值： U 正弦电流、电压的有效值
一般规定：|y |
上页下页
例
100
i
50
已知正弦电流波形如图，＝103rad/s，（1）写出i(t)表达式；（2）求最大值发生的时间t1
t
t1
解 i ( t ) 100 cos(103 t y )
0
t 0 50 100 cosy
y 3
由于最大值发生在计时起点右侧
上页下页
Iy 为正弦量 i(t) 对应的相量。称 I
Iy i(t ) 2I cos( t y ) I
相量的模表示正弦量的有效值相量的幅角表示正弦量的初相位同样可以建立正弦电压与相量的对应关系：
Uθ u( t ) 2U cos( t θ ) U
| A1 | ( θ1 - θ2 ) | A2 |
复数除法：模相除，角相减。
上页下页
例1
547 10 - 25 ?
解 547 10 - 25 ( 3.41 j 3.657) (9.063 - j 4.226)
12.47 - j 0.569 12.48 - 2.61
解
相量图
i 50 2cos(314t 15 ) A
在复平面上用向量表示相量的图
j
=Iy i ( t )= 2 I cos( t+y ) I
U
Uθ u( t ) 2U cos( t θ ) U
I

y
1
上页下页
4. 相量法的应用
（1）同频率正弦量的加减
180.2 j126.2 2 .238 j 6 .329
182.5 j132.5 225.536
上页下页
(3) 旋转因子
e
j
cos j sin 1
相当于A逆时针旋转一个角度θ ，而模不变。故把 e jθ 称为旋转因子。
Im
A· e jθ
对于任意一个正弦时间函数都有唯一与其对应的复数函数
i 2 I cos( t+y ) A( t ) 2 Ie j ( t+y )
Re[A( t )] Re[ 2 I e
jy
e
j t
e j t ] ] Re[ 2 I
复常数 A(t)包含了三要素：I、 y 、ω ，复常数只包含了I , y 。
例2
(17 j 9) (4 j6) 220 35 ? 20 j 5

19 . 24 27 . 9 7 . 211 56 . 3 解原式 180.2 j126.2 20.6214.04
180.2 j126.2 6.72870.16
u1 ( t ) 2 U 1 cos( t y 1 ) u2 ( t ) 2 U 2 cos( t y 2 )
u(t ) u1 (t ) u2 (t )
8.1 正弦量的基本概念
1. 正弦量
瞬时值表达式：波形：
y
O
i
T
i ( t ) I m cos(t y )
正弦量为周期函数
t
f ( t ) f ( t kT )
周期T (period)和频率f (frequency) :
1 f T
单位：Hz，赫(兹)
上页下页
周期 T ：重复变化一次所需的时间。单位：s，秒频率 f ：每秒重复变化的次数。
u, i u u i o
j ＝ 0，同相
u, i
t
i
u, i u i
o
t
j=/2
u 领先 i于/2, 不说 u 落后 i于3/2； i 落后 u于/2, 不说 i 领先 u于3/2。
o
t
同样可比较两个电压或两个电流的相位差。
上页下页
例
计算下列两正弦量的相位差。
(1) i1 ( t ) 10 cos(100 t 3 4) j12 3 4 - (- 2) 5 4 j12 -2 5 4 - 3 4 i2 ( t ) 10 cos(100 t - 2)
同频正弦量的相位差等于初相位之差。
u, i y u uy O 规定： |j |
i
i
j ui
t
j ui > 0， u 超前于i，或i 落后于u ，u 比i先到达最大值；

j ui < 0， i 超前于u ，或u 滞后i ，i 比 u 先到达最大值。
上页下页
特殊相位关系
j = ，反相
复数运算 (1)加减运算——采用代数形式

a
Re
或
a | A | cosθ b | A | sinθ
Im A2
图解法
若：A1 a1 jb1 , A2 a2 jb2 则：A1 A2 (a1 a2 ) j(b1 b2 )
A1
0 Re
上页
下页
(2) 乘除运算——采用极坐标形式
故＋j, －j, －1 都可以看成旋转因子。
上页
下页
3. 正弦量的相量表示
构造一个复函数
A( t ) 2 Ie j ( t y )
2 Icos( t y ) j 2 Isin( t y )
对A(t)取实部：
Re[ A( t )] 2 Icos( t y ) i ( t )
1 2
不能比较相位差
i2 (t ) 3 cos(100 t - 150)
j12 -30 - (-150) 120
两个正弦量进行相位比较时应满足同频率、同函数、同符号，且在主值范围比较。
上页下页
4. 周期性电流、电压的有效值
周期性电流、电压的瞬时值随时间而变，为了衡量其效果，在工程上采用有效值来表示。
( 2) i1 ( t ) 10 cos(100 t 30) i2 ( t ) 10 sin(100 t - 15)
i2 (t ) 10 cos(100 t - 105) j12 30 - (-105) 135
( 3) u1 ( t ) 10 cos(100 t 30) u2 ( t ) 10 cos(200 t 45) (4) i1 ( t ) 5 cos(100 t - 30) i2 ( t ) -3 cos(100 t 30)
A e
j

o Im
A Re
几种不同值时的旋转因子

2
, e
j

2
cos

2
j sin

2
jA
j
A
Re
- jA
-j 0 - , e 2 cos(- ) j sin( - ) - j 2 2 2 -A j , e cos( ) j sin( ) -1
Im b A |A|

正弦量的相量表示

合集下载

正弦量的相量表示

2.2正弦量的相量表示法

正弦量的相量表示法

正弦量的相量表示及运算

《电工电子技术》课件——正弦量的相量表示法

正弦量的相量表示

正弦量的相量表示

电路3-2正弦量的向量表示法

5-3 正弦量的相量表示法

电工基础049.第49课时.正弦量的相量表示

3.2 正弦量的相量表示法

正弦量的相量表示

正弦量的相量表示法

电路分析基础：正弦量的相量表示法

文档推荐

最新文档