当前位置：文档之家 › 正弦量的向量表示法..

正弦量的向量表示法..

  • 格式：ppt
  • 大小：308.50 KB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

正弦量的三要素及相量表示法基尔霍夫

正弦量的三要素及相量表示法基尔霍夫
第五章
正弦电流电路导论
内容提要
1.正弦量的相量表示法； 2.两类约束的相量形式； 3.正弦电流电路的分析计算； 4.正弦电流电路的功率。
5.1 正弦量电压和电流的基本概念
一 时变的电压和电流 ◆ 时变电压和电流：随时间变动的电压和电流。
第五章
正弦电流电路
u(t )
◆瞬时值：时变电压和电流在任一时刻的数值，用 和 i (t ) 表示。
2π u2 =100 2sin(100t )V 3
3
0
6
I1
解：
π I1 =50 A 6 π U1 =100 V 3 2π U 2 =100- V 3

2 3
U 2
相量图
第三章 正弦电流电路
四 用相量求正弦量的和与差
i1 (t ) 70.7 2 sin(ωt 45 )A i2 (t ) 42.4 2 sin(ωt 30 )A
③角频率ω：每秒变化的弧度。单位：弧度/秒(rad/s)
第五章 正弦电流电路
三者间的关系：
1 f T
2 2 f T
* 电网频率（工频）：我国：50Hz；美国和日本：60Hz * 无线通信频率： 30 kHz ～ 30GMHz ◆ 相位和初相位 ①相位：正弦波的 (ωt ψ ) 。 ②初相位 ：t =0 时的相位。 ③规定：初相位的绝对值不超过π。
第五章 正弦电流电路
三 用相量表示正弦量
相量：表示正弦量的复数称为相量。
相量表示法：用模值等于正弦量的最大值（或有效值）、
辐角等于正弦量的初相的复数对应地表示相应的正弦量。
即：相量 Im （或 I ）
j
模用最大值表示时，为最 I ψ 大值相量，即 I m m

正弦量的相量表示法教案

正弦量的相量表示法教案

《电工学（少学时）》第三章正弦量的相量表示法学习目标： 1. 掌握复数的基本知识。

2 ．掌握正弦量的相量表示法。

重点：正弦量的相量表示法。

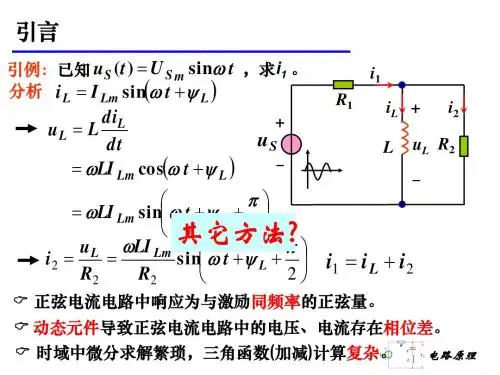
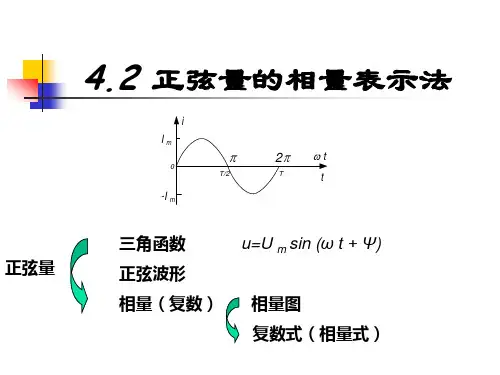
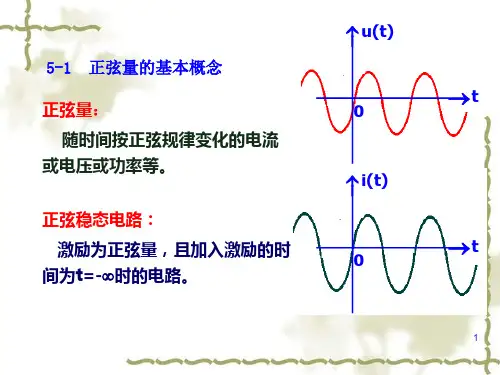
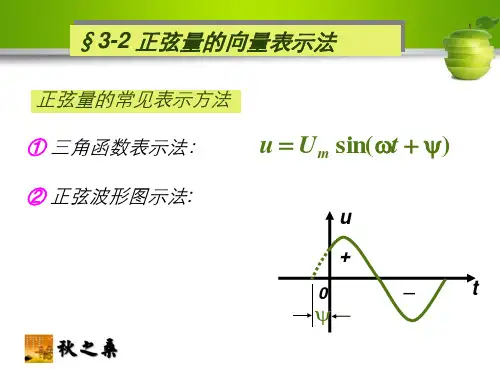
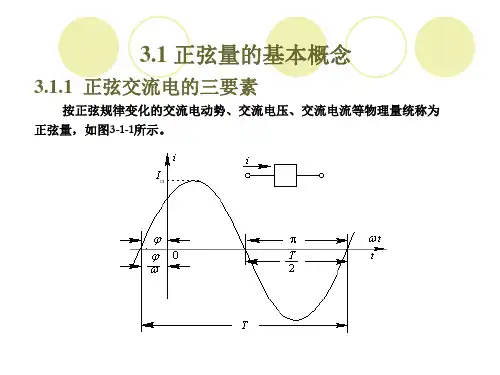
难点：相量图一、相量法的引入一个正弦量可以用三角函数式表示，也可以用正弦曲线表示。

但是用这两种方法进行正弦量的计算是很繁琐的，有必要研究如何简化。

由于在正弦交流电路中 , 所有的电压、电流都是同频率的正弦量，所以要确定这些正弦量，只要确定它们的有效值和初相就可以了。

相量法就是用复数来表示正弦量。

使正弦交流电路的稳态分析与计算转化为复数运算的一种方法。

二、复数概述1 ．复数：形如的式子称为复数，为复数的实部，为复数的虚部，、均为实数，为虚数单位。

图 4-3 复数的图示法2 ．复数的图示法式中为复数 A 的模，为复数 A 的辐角。

3 ．复数的表示形式及其相互转换其中代数式常用于复数的加减运算，极坐标式常用于复数的乘除运算。

4 ．复数的运算法则①相等条件：实部和虚部分别相等（或模和辐角分别相等）。

②加减运算：实部和实部相加（减），虚部和虚部相加（减）。

③乘法运算：模和模相乘，辐角和辐角相加。

④ 除法运算：模和模相除，辐角和辐角相减。

三、相量表示法1 ．正弦量与复数的关系= sin( ψ )= [ ]= [ ]正弦电压等于复数函数的虚部，该复数函数包含了正弦量的三要素。

2 ．相量 ---- 分有效值相量和最大值相量① 有效值相量：= / ψ② 最大值相量：= / ψ3 ．相量图在复平面上用一条有向线段表示相量。

相量的长度是正弦量的有效值I ，相量与正实轴的夹角是正弦量的初相。

这种表示相量的图称为相量图。

例 4-4 ：。

写出表示 1 和2 的相量，画相量图。

解： 1 =100 /60 ° V2 =50 /-60 ° V相量图见图 4-4 。

例 4-5: 已知 1 =100 sin A ， 2 =100 sin( -120 ° )A ，试用相量法求 1 + 2 ，画相量图。

正弦量的向量表示

正弦量的向量表示

试求uAB ，并画出相量图。
解:(1) 用相量法计算：
UA 220 0 V
N
UB 220 120V
UC 220 120V
+ +A
UA
–
U–B
UAB -
N
+– U+–C
B C
由KVL定律可知
UAB UA UB 220 0V 220 120 V
UAB 220 V 220 cos (120 ) jsin (120) V
【例3】已知同频率的正弦量的解析式分别为
i=10sin(ωt+30°), 并绘出相量图。
, 写出电流和电压的相量
,
u 220 2 sin(t 45)
••
I 、U
【例 1】
•
I
10
30 5 2 30A
2
•
U
220
2
45V
2
相量图如图所示。
＋j ·I
30°
O
45°
＋1
U·
注意:
①相量只是表示正弦量，而不等于正弦量。
Um、U、Im、I
复数及四则运算
1.复数
A a jb
模 r A a2 b2
辐 角
arctan b
a
( 2 )
a r cos
b
r sin
＋j b
r
O
P a ＋1
2. 复数的四种形式 (1) 复数的代数形式
(2) 复数的三角形式 (3) 复数的指数形式 (4) 复数的极坐标形式
A a jb
A r cos jrsin
A re j
A r A
3、相量表示法

5-3 正弦量的相量表示法

5-3 正弦量的相量表示法

或
I m Ime
j i
I m i
I Ie
I i
电路原理
§5-3 正弦量的相量表示法 相量 正弦量
j u
Um U m e
u(t ) Im(Ume ) u(t ) Im( 2Ue )
i (t ) Im( I me
j t
j t
U U u
I m Ime
A2 A2e j 2 A2 2 a2 jb2
加减运算 A1 A2 (a1 a2 ) j (b1 b2 )
j ( ) 乘法运算 A1 A2 A1 A2e 1 2 A1 A2( 1 2 )
A1 A1 j ( 1 2 ) A1 除法运算 e ( 1 2 ) jA1 A2 A2 A2 j 1 90o jA1 A1e A1 1 90o
e jt Im 2U e jt ut Im U m




2)相量运算与复数运算相同，但必须是同频率的相 量才能进行运算。 3)已知时间正弦量可唯一确定对应的相量，而相量 只包含了正弦量的两个要素。 、 U U m 、U 4)注意符号区分：ut 、 、U m
正弦量 幅值 有效值 幅值相量 有效值相量
Im(虚部)


b1
A1
A1
a1
A1 j 1 90 o jA1 A1e A1 1 90o j
1
Re(实部)


0
jA1
电路原理
§5-3 正弦量的相量表示法
常用相量表示形式：
Ue j U
U U U (cos j sin ) U

4.2 正弦量的相量表示法

4.2 正弦量的相量表示法

(1)2+(2)2
Im
I1m cos 1 I2m cos 2 I1m sin 1 I2m sin 2
2
2
(1)÷(2)
I1m sin 1 I2 m sin 2 arctan I cos I cos 1m 1 2m 2
将本题中 的I1m=100A, I2m=60A, Ψ1=45°, Ψ2=-30°
代入可得：
Im
70.7 52
2
70.7 30 129A
2
70.7 30 ' arctan 18 20 70.7 52
故得
i=129sin(ωt+18°20′)A

4.2 正弦量的相量表示法
i Im
0

T/2
2
T
t
t
-I m
三角函数
u=U m sin (ω t + Ψ) 相量图 复数式（相量式）
正弦量
正弦波形
相量（复数）
4.2.1 旋转有向线段表示正弦量
a. 在 u=U m sin (ω t + Ψ) 中
y A
Um 表示正弦电压的最大值 （A的长度） ω 表示正弦电压的角频率 Ψ 表示正弦电压的初相位
c.复数的三种表示方法： A=a+j b 实部
a2 b2 b arcty a r
b
虚轴 +1 A r

虚部
0 a
实轴 +1
a=r cos ψ
b=r sin ψ
复数的模 复数的辐角
A=a+j b= r cos ψ+j r sin ψ = r (cos ψ + j sin ψ)

第二节正弦量的相量表示法第三节电阻元件伏安关系的向

第二节正弦量的相量表示法第三节电阻元件伏安关系的向

i(t) 11.18 2 cos(t 10.3) 21
例2 图示电路，已知：
+ u1(t) -
u1(t) 6 2 cos(t 30)
-
u2 (t) 4 2 cos(t 60)
u3(t)Biblioteka u2(t)+
求 u3(t)
解： 正弦量以相量表示，有
•
U1 630
•
U2 460
•
••
U3 U1 U2 (5.19 j3) (2 j3.45)
u(t) 2U cos(t u )
p(t) 2U cos(t u ) 2I cos(t i )
UI cos(2t 90)
2）平均功率: P 1
T
p(t)dt
T0
0
p(t)
UI
3）无功功率: Q UI
X
LI
2
U X
2 L
(Var)
0
意义:反映电感元件与电源进行能量交换的最大速率.
t
12
i(t) 2I cos(t i )
u(t) 2U cos(t u )
p(t) 2U cos(t u ) 2I cos(t i )
UI cos(2t 90)
2）平均功率: P 1
T
p(t)dt
T0
0
3）无功功率: Q UI
XCI 2
U2 XC
(Var)
p(t)
UI
0
意义:反映电容元件与电源进行能量交换的最大速率.
3 j4
8 j6
例2：写出下列正弦量的时域形式：
•
U1 3 j4
•
U 2 8 j6
u1(t) 5 2 cos(t 126.9)

正弦量的向量表示法

正弦量的向量表示法
arctg (70.7 30) 1820
70.7 52
i 129sin(t 1820)A
③ 正弦量的复数表示法
复数简介
一、复数的几种表示形式 1. 代数形式（直角坐标形式）
A a jb j 1
a 称为实部
b称为虚部
均为实数，复矢量 在实、虚轴的投影
2. 三角形式
则 A a jb cos j sin
六、相量运算
•
设： A e j 则
•
•
B A e j e j( )
当 90时
••
•
B A e j90 e j( 90) j A
e j90 cos90 j sin 90 j
••
•
C A e j90 e j( 90) j A
••
•
•
D A e j90 • e j90 A e180 A
•
Um 200 220V
•
U 20020V 200e j20V
但不能写成：
u 200 2 sin(314 t 20) 200 220 200 2e j20
•
例2： 已知 f 1000Hz, I 0.530 A, 求i。
解： 2f 6280rad / s
i 0.5 2 sin(6280t 30) A
注意：① 幅值相量正弦量，它们存在一定得对应关系。
•
U m Ume ju Umu u Um sin(t u )
② 幅值相量反映了振幅和初相位的两个要素。
•
U m Ume ju Umu
③ 旋转因子 ejt 反映了另一要素t。
例1： u 200 2 sin(314 t 20)V
其相量形式：
i2 I 2m sin(t 2 ) 60 sin(t 30) A

电工基础3、3正弦量的相量表示法

电工基础3、3正弦量的相量表示法

1、复数的几种表示方法
复数的代数表达式为： A=a+jb
复数的三角形式为： A=rcos θ +jrsin θ
复数的极坐标形式为： A=r θ
复数的指数形式为: A=re j θ
2、加减运算
•A±B=(a1±a2)+j(b1±b2)
3、乘除运算
A·B=r1r2 θ1+θ2
A r1 1 2
A
数A的幅角； A在实轴上的投影a是它的实部； b
r

A在虚轴上的投影b称为其虚部。 0 a
＋1
复数A的代数表达式为：A=a+jb 由图又可得出复数A的模r和幅角θ分别为：
r a2 b2 极坐标形式： A=r θ
arctan b
a
＋j
br

0 a
A 由图还可得出复数A与模 a r cos
Z1Z2 3 00 ×3 -900 = 9 -900
Z1 Z2
3-j3
3 2 -450
= 2.12 -450
1. 已知复数A=4+j5，B=6-j2。试求A+B、 A-B、A×B、A÷B。
2. 已知复数A=30 30°，B=40 60°。试 求A+B、A-B、A×B、A÷B。
A+B=（4+6）+j（5-2）=10+j3≈10.4 16.70
3.3.1
1、复数的图形表示
1）复数用点表示
A1=1+j A2=-3 A3=-3-j2 A4=3-j
复数及其运算规律
+j
3
2
A2
1
A1
-3 -2 -1 0 1 2 3 +1

正弦量的向量表示法详解

正弦量的向量表示法详解

P 0
t 0
a +1
b
P2
2
Um u Um sin( t )V
P1
t2 0 t1
t
P2
Um
※旋转矢量与瞬时值之间的关系
j Um
P0 t 0
Um u Um sin( t )V
P
b t
P
t
a
0
1 0 t
t
Um
u
OP=Um cos (t+) + j Um sin(t+)
= Um e j(t+) = Um t +
五、相量图
按照各个正弦量的大小和相位关系用初始位置的 有向线段画出的若干个相量的图形，称为相量图。
在相量图上能形象地看出各个正弦量的大小和 相互的相位关系。
例： i Im sin(t i ) A
u Um sin(t u ) V
•
U Uu V
•
I Ii A
注意
不同频率的正弦量，不能在在同一张图上用相量表示。
e180 cos180 j sin180 1
例：已知 i1 2I1 sin( t 1) A i2 2I2 sin( t 2 ) A
求 i i1 i2
解：
i
i1
i2
Im
2
•
I
1
e
jt
Im
2
•
I
2
e
jt
i2 I 2m sin(t 2 ) 60 sin(t 30) A
试求总电流 i 。
i
i2 i1
解 用三角函数式求解 i i1 i2 I1m sin(t 1 ) I 2m sin(t 2 ) I1m (sint cos1 cost sin1 ) I 2m (sint cos 2 cost sin 2 ) (I1m cos1 I 2m cos 2 ) sin t (I1m sin1 I 2m sin 2 ) cost

正弦量的相量向量法

正弦量的相量向量法
I& I&1 I&2 553.1o 4 90o (3 j4) j4 3A
i(t) 3 2 cost A
返回
X
4.向量图
如果将相量在复平面上表示出来，则称为相量图。相
量图表示了同频率的各正弦量之间的相位关系。
+j
I1
53.1 o 90 I +1
I2
例2中各相量的相量图
返回
X
内容提要
变换方法的概念 正弦量的相量表示 相量的线性性质和微分性质 相量图
X
1.变换方法的概念
求解指数方程：x2.65 5 两边取对数 2.65lg x lg 5
lg x lg 5 2.65 0.2637
x lg1 0.2637 1.835
原来的问题 直接求解
原来问题 的解答
变换
反变换
变换域中 较易的问题
求解
变换域中 问题的解答
X
1.变换方法的概念
变换方法的基本思路： 1）把原来的问题变换为一个比较容易处理的问题。 2）在变换域中求解问题。 3）对变换域中求得的解答进行反变换得到原来问 题的解答。
返回
X
2.正弦量的相量表示
欧拉公式：ej cos jsin
用t 代替 两边同乘以常数 Fm
dt
推广到 n 阶导数：
f
(n)(t)
dn f (t) dt n
(j )n F
X
例题2 已知 i1(t) 5 2 cos(t 53.1o)A, i2(t) 4 2 sint A 。求i(t) i1(t) i2(t) 。
解：写出正弦量的相量。
i1(t) I1 553.1 A
i2(t) 4 2 cos(t 90o)A i2(t) I2 4 2 90 A

正弦量的基本概念正弦量的相量表示法电容元件

正弦量的基本概念正弦量的相量表示法电容元件

3.旋转因子及旋转相量
相量与ejwt相乘是一个随时间变化的函数，它随时
间的推移而旋转，且旋转速度为ω。我们把相量乘
以ejwt再乘以常数 2 称为旋转相量，旋转相量在虚 轴上的投影Imsin(ωt+φi)为正旋量的瞬时值。 Imsinφi为i(t)的初始值，如图3-2-1（b）所示。
所以也可以用正弦相量来表示正旋量。
0
2T
I
Im 2
0.707Im
U
Um 2
0.707Um
Um 220 2 311V
例 3-4 一个正弦电流的初相角为60°,在T/4 时 电流的值为5A，试求该电流的有效值。
解 该正弦电流的解析式为
it I m sin wt 60 A
代入已知量有：5
Im
sin wT 4
60 A
5
Im
sin
2
3
A
则有：I
＝
m
5
sin5
/ 6
5 1
10A
2
I I m 7.07A 2
3.2 正弦量的相量表示法
复数及四则运算
1.复数 在数学中常用A=a+bi表示复数。其中a为实部, b为虚部,
i 1 称为虚单位。在电工技术中, 为区别于电流的符
号, 虚单位常用j表示。 ＋j
3
A
O
确定φ角正负的零点均指离计时起点最近的那个零点
i i1＝Imsint
i i2＝Imsin(t＋ 2)
i i3＝Imsin(t＋ 6)
i
i4＝Imsin(t－
6)
0
t 0
t 0
t 0
t
2
6
6

3.2 正弦量的相量表示法

3.2 正弦量的相量表示法

所以：i sin(t 30 ) sin(t 150 )
3、 = 2–1=90°正交
(1)用相量图叠加
如： i1 =3sin(ωt +30°) i2 =4sin(ωt +120°)
求和
则： Im= Im12 + Im22 = 5
θ =arctan(对边/邻边) = 53°
(本例）=1+θ =83° i=5sin(ωt+83°)
现有复数A =|A| e j
相量图
A
+1
若令：A• j =|A| e j ·e j 90° 则有：A• j = |A|e j ( + 90°)
由此知，A j使A逆时针旋转90°
相量图 Aj
90°
A
同理， A（- j）使A顺时针旋转90° 故：复平面中，j 是旋转90°的算子符。
+1
接3.3
4.复数的极坐标形式 A = A
复数的四种表示形式，是相量表示法的基础。
3.2.2 正弦量的相量表示法 +j
一、正弦量的相量表示法
b(t)
若，令复数A绕原点， 以ω的角速度、 逆时针方向旋转，
A
ω
A ωt
+1
则，任何时刻(t)，其虚部的表达式为：
b(t)=|A|sin(ωt +)
形式完全相同
i(t)=Imsin(ωt +)
但当由相量式写解析式时，必须将频率写入。
三、相量表示法举例 例1. i=5 2 sin(ωt+30 °) 极大值相量式： Im=5 2∠30° 有效值相量式： I =5∠30°
相量图
5 Iω
30°
+1

正弦量的向量表示

正弦量的向量表示

2、波形图表示法
u
O
ωt
【例2】画出正弦交流电 i 15 sin(314 t
的波形图。

4
)A
【练习2】画出正弦交流电
i 20 sin(100 t

2
)A
的波形图。
3.正 弦 量 的 相 量 表 示 正弦交流电的旋转向量表示法，为了区别 与其他的向量表示， 将表示正弦交流电的向量称为相量。 符号表示：大写字母加黑点。
AB
220 ( 1 0.5 j 0.866 )V
220 1.73 30V
U C
-U B
U AB U A
380 30 V
所以uAB 380 2 sin ( ω t 30 )V
(2) 相量图
30
U B
思考题
1、写出下列各正弦量对应的向量，并绘出向 量图。
+ A
U AB N
U C +
–
–
220 0 V U A 220 120V U B 220 120V U C
U B +
–
B C
由KVL定律可知
U U 220 0 V 220 120 V U AB A B 220 V 220 cos量的表示法
1、解析式表示法
u Umsin( t )
必须 小写
【例1】已知某正弦交流电压的最大值为 311V，频率50Hz，初相30°，求它的解析 式表达式和0.01s时刻的电压值。
【练习1】已知某正弦交流电流的最大值为 20A，频率50Hz，初相-60°，求它的解析 式表达式和0.05s时刻的瞬时值。

正弦交流电路的向量表示法

正弦交流电路的向量表示法

解 A1的模 r1 42 (3)2 5
辐角
1
arctan
3 4
36.9
（在第四象限）
则A1的极坐标形式为 A1=5 -36.9°
A2的模 r2 (3)2 42 5
辐角
2
arctan 4 3
126.9
(在第二象限)
则A2的极坐标形式为 A2 5/126.9
例
写出复数A=100 30°的三角形式和代数形式。 解 ： 三角形式A=100（cos30°+jsin30°
＋1
图4.9 复数相加减矢量图
复数及四则运算（四）
(2) 复数的乘除法
A B r1 1 r2 2 r1 r2 1 2
A r1 1 r1 B r2 2 r2
1 2
例
求复数A=8+j6 , B=6-j8之和A+B及积 A·B。
解： A+B=（8+j6)+(6-j8)=14-j2 A·B=(8+j6)(6-j8)=10/36.9°·10
思考题（一）
1、写出下列各正弦量对应的向量，并绘出向量 图。
(1) u1 220 2 sin(t 100 )V
(2) u2 110 2 sin(t 240 )V (3) i1 10 2 cos(t 30 ) A (4) i2 14.14sin(t 90 ) A
思考题（二）
2、写出下列向量对应的解析式（f=50Hz)。
代数形式A=100(cos30°+jsin30°)=86.6+j50
复数及四则运算（三）
3. 复数的四则运算
＋j A1＋A2
(1) 复数的加减法
A1 a1 jb1 r1 1 A2 a2 jb2 r2 2

正弦量的相量表示法及计算法

正弦量的相量表示法及计算法

则：
U1 U2
U1 U2
1 2
（4）相等运算
设 U1 U2 用极坐标式表示时 U1 U2 , 1 2 用代数式表示时 a1 a2 , b1 b2 （5）相反运算
设 I1 I2 用极坐标式表示时 U1 U2 , 1 2 180 用代数式表示时 a1 a2 , b1 b2
[例3—2]见教材。
解：
I (3 j4) 3+j4=5(53.13 180 ) 5126.87 A
分析：求相反相量 就是将原相量旋转 180o ，相量图上两 相反相量对称于原 点，如图所示。
3.2.4 基尔霍夫定律的相量形式
对于正弦交流电路任一节点，有
i 0,u 0
一、KCL的相量形式： I 0
二、KVL的相量形式： U 0
内容简介
本教材理论推导从简，计算思路交待详细，概念述 明来龙去脉，增加例题数量和难度档次，章节分 “重计 算”及“重概念”两类区别对待，编排讲究逐步引深的 递进关系，联系工程实际，训练动手能力，尽力为后续 课程铺垫。借助类比及对偶手法，语言朴实简练，图文 印刷结合紧密，便于自学与记忆，便于节省理论教学时 数。适用于应用型本科及高职高专电力类、自动化类、 机电类、电器类、仪器仪表类、电子类及测控技术类专 业。
A( 90)
“j”的数学意义和物理意义
旋转 90因子： j
j cos 90 jsin 90
设相量 A r
B +j
• 相量A 乘以 j ，
A
A 将逆时针旋转 90 得到 B
• 相量A 乘以 j ， A o
ψ
+ 1
将顺时针旋转 90，得到 C
C
3. 除法运算
设： U1 U11 U2 U22

正弦量的三种表示方法

正弦量的三种表示方法

正弦量的三种表示方法
正弦量，又称正弦函数，是圆周率π（π）及其复数系统中理想的一类
函数，是微积分中最重要的函数之一。

以下是正弦量的三种表示方法：
一、极坐标表示法：用极坐标形式表示的正弦函数如下所示：
sinθ=r
其中r为取值范围为[-1, 1]，θ为弧度，等于π/180度。

此外，对于任意
角度来说，其正弦值都是固定的，即r是一个常量。

二、标准正弦函数：用标准正弦函数表示的正弦函数如下所示：
y=sin x
x为自变量，取值范围为[-π, π]，y为复变量，取值范围也在[-1, 1]之间。

根据此法可以更明确地获得相应的正弦值。

三、三角正弦函数：三角正弦函数也叫做三角函数，用三角正弦函数
表示的正弦函数如下所示：
y=sin θ
其中θ为角度，取值范围[0, 360]，y为正弦值。

得到的结果与极坐标表示法相同，即：r=sinθ，但结果显示时更具有可读性。

第19讲 正弦量的相量表示法

第19讲 正弦量的相量表示法

j 1 虚数单位
+j 复平面 b A 式中: a r cos ψ 虚 r b r sin ψ 轴 a +1 0 实轴 r a 2 b 2 复数的模
A=a + jb
b ψ arctan 复数的辐角 a
（二）复数的三角函数形式
A r cos ψ j r sin ψ r (cos ψ j sin ψ )
j 0 1900
故可把＋j看成是一个模为1，辐角为900的复 数，所以， jA1=1 900· A1=A1 ψ1+900 任一复数乘以＋j时，其模不变，幅角增大 900，相当于在复平面上把复数矢量逆时针方向旋 转900。 同理： -jA1=A1 ψ1-900
（五） “j”的数学意义和物理意义
（三）复数的指数形式
A re
由欧拉公式:
jψ
e j ψ e j ψ e j ψ e j ψ cos ψ , sin ψ 2 2j
可得:
e
jψ
cos ψ j sin ψ
A r ψ
jψ
（四）复数的极坐标形式
A a jb r cos j r sin re r ψ
• 【能力训练】 已知正弦电流，，求其电流相量， 画出相量图，并求出i(t)=i1(t)+i2(t)。 • 解：表示正弦电流 i1(t ) 5 sin(314t 60)A 的相量 为 I 5e j60 A 560 A

1m
•
i2 (t ) 10 cos(314t 120 )A 10sin(314t 120 90 180 )A 10150 A 10sin(314t 150 )A I

电路分析基础正弦量的相量向量法

电路分析基础正弦量的相量向量法
基尔霍夫定律的相量形式 R、L、C元件VCR的相量形式
X
1.基尔霍夫定律的相量形式
线性非时变电路在单一频率的正弦激励下（正弦电 源可以有多个，但频率完全相同）进入稳态时，各 处的电压、电流都为同频率的正弦量。 KCL的时域形式：
i
k 1
K
k
0
j t K k 1
ik
k 1
K
j t Re[ I e ] Re[ I e km km ] k 1
线性非时变电路在单一频率的正弦激励下正弦电源可以有多个但频率完全相同进入稳态时各处的电压电流都为同频率的正弦量
§7-2 正弦量的相量 相量法
北京邮电大学电子工程学院
退出
开始
内容提要
变换方法的概念 正弦量的相量表示 相量的线性性质和微分性质 相量图
X
1.变换方法的概念
2.65 求解指数方程： x 5 两边取对数 2.65lg x lg 5
du d j t i (t ) C C {Re[ 2Ue ]} dt dt j t Re 2(j CU )e
I

U

1 j C
X
2.R、L、C元件VCR的相量形式
I I i j CU j CU u I CU CU u 90 i u 90
X
3.相量的线性性质和微分性质
若： f ( t ) F F
d f ( t ) 则 ：f ( t ) j F F 90 dt
'
推广到 n 阶导数：
n d f (t ) ( n) f (t ) dt n

(j ) F
n
X
例题2 已知 i1 (t ) 5 2 cos( t 53.1ห้องสมุดไป่ตู้)A ,

正弦量的相量表示法-J

正弦量的相量表示法-J

ITSM / ITIL
• 6、 • 需要强调的是： • 1）只有同频率的正弦量，其相量才能
相互运算，才能画在同一个复平面上。
• 2）画在同一个复平面上表示相量的图 称为相量图。
• （课本P37）
Copyright © Sino-i Technology Limited All rights reserved
Copyright © Sino-i Technology Limited All rights reserved
Sino-i Technology Ltd.
2、正弦量相量的书写方式
设正弦量: u Umsin( ωt ψ)
用相量表示:
U Ue j ψ U ψ
相量的模=正弦量的有效值 相量辐角=正弦量的初相角
21
Sino-i Technology Ltd.
ITSM / ITIL
4、
• 正弦量的相量表示法中，在表示相量 的大写字母上打点“·”是为了与一般 的复数相区别。 （课本P37）
Copyright © Sino-i Technology Limited All rights reserved
22
Sino-i Technology Ltd.
5
Sino-i Technology Ltd.
ITSM / ITIL
• 1. 复数的图形表示 • 1） 复数用点表示
A1=1+j A2=-3 A3=-3-j2 A4=3-j
＋j
3
2
1
A1
A2
－ 3 － 2－ 1 0 1 2 3 ＋ 1
－1
－2
A4
A3
－3
Copyright © Sino-i Technology Limited All rights reserved
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

i i2
因此，总电流 i 的幅值为
I m (I1m cos 1 I 2m cos 2 ) (I1m sin 1 I 2m sin 2
总电流 i 的初相位为

2
i1
1 2 2 )

I1m sin 1 I 2m sin 2 arctg ( ) I1m cos 1 I 2m cos 2
则
A a jb cos j sin
与代数形式的关系
a cos a 2 b 2 或 b b sin arctg a
2001-02-10
南京航空航天大学
3. 指数形式 由欧拉公式：
e
j
cos j sin
§3-2 正弦量的向量表示法
正弦量的常见表示方法 ① 三角函数表示法： ② 正弦波形图示法:
u U m sin( t )
u
+ _

2001-02-10 1 sin( t 1 ) A
i i1 i2
i
i2 2I 2 sin( t 2 ) A
Ume
j ( t u )
Um cos(t u ) jUm sin(t u )
很明显，上式的虚部恰好是 u，即
u I m U me
2001-02-10

j (t u )
U
m
sin(t u )
南京航空航天大学
u I m U m e j (t u ) I m U m e j u e jt jt I m U m e
式中 ①





Im [ ] 为取“虚部”的运算符。
U m U m e ju U m u
称为正弦量 u 的“幅值相量” 同样有： U U Ue j

（最大值相量） 有效值相量
2001-02-10
南京航空航天大学
相量 U m 正好体现了正弦量的量特征：初相、幅值，而没能体现t。
Um
u U m sin( t )V
b t t a
P

1
0

0 t
t
Um
u
OP=Um cos (t+) + j Um sin(t+)
= Um e j(t+)
2001-02-10
= Um t +
南京航空航天大学
四、利用向量表示正弦交流量
设正弦电压
u U m sin(t u )
i1 i2
求
i i1 i2 2 I1 sin( t 1 ) 2 I 2 sin( t 2 ) ......
2001-02-10
南京航空航天大学
例题 分析
• 对如图电路，设
i i2
i1 I1m sin(t 1 ) 100sin(t 45) A
南京航空航天大学
2001-02-10
由此，代入数据I m1=100A, I m2=60A, 1=45, 2= –30 则：
Im (70.7 52) 2 (70.7 30) 2 122.7 2 40.7 2
129A
70.7 30 arctg ( ) 1820 70.7 52
A B = 1 2 ( 1 + 2)
2001-02-10 南京航空航天大学
B=a2+jb2= 22
三、旋转矢量 设
A A
e
jt
1t
——称为旋转因子（ ejt ）
则Ae jt
表示将A逆时针旋转一角度t
故称 A e jt 为旋转矢量。
2001-02-10
复数 A (cos j sin ) e j
4. 极坐标形式
A
2001-02-10
南京航空航天大学
二、复数运算
加、减宜用代数形式 例：A=a1+jb1 B=a2+jb2
A B = (a1 a2) + j(b1 b2)
乘、除宜用极坐标形式 例： A=a1+jb1=11
i2 I 2m sin(t 2 ) 60sin(t 30) A
i1
试求总电流 i 。
解 用 三 角 函 数 式 求 解
i i1 i2 I 1m sin(t 1 ) I 2 m sin(t 2 ) I 1m (sin t cos 1 cost sin 1 ) I 2 m (sin t cos 2 cost sin 2 ) ( I 1m cos 1 I 2 m cos 2 ) sin t ( I 1m sin 1 I 2 m sin 2 ) cost
i 129sin(t 1820) A
2001-02-10
南京航空航天大学
③ 正弦量的复数表示法
复数简介
一、复数的几种表示形式 1. 代数形式（直角坐标形式）
A a jb
j 1
a 称为实部
b称为虚部
2001-02-10

均为实数，复矢量 在实、虚轴的投影
南京航空航天大学
2. 三角形式
南京航空航天大学
正弦量的旋转矢量表示
Um
P1
a1 a2
+j
t
P0 t 0
Um
u U m sin( t )V
b b1
t 2
t1
0
P1
a
+1

0 t1
t 2
t
P2
b2
Um
P2
2001-02-10
南京航空航天大学
※旋转矢量与瞬时值之间的关系
Um
P
j
P0 t 0
2001-02-10 南京航空航天大学
两个同频率正弦量相加仍得到一个正弦量，设此正弦量为
i I m sin( t ) I m cos sin t I m sin cos t
则
I m cos I1m cos 1 I 2m cos 2 I m sin I1m sin 1 I 2m sin 2
但对于分析线性电路来说，电路中电压、电流都是和电源同频率的正弦量。

注意：① 幅值相量正弦量，它们存在一定得对应关系。
U m U me