电工技术——正弦量的相量表示法

《电工学（少学时）》第三章正弦量的相量表示法学习目标： 1. 掌握复数的基本知识。

2 ．掌握正弦量的相量表示法。

重点：正弦量的相量表示法。

难点：相量图一、相量法的引入一个正弦量可以用三角函数式表示，也可以用正弦曲线表示。

但是用这两种方法进行正弦量的计算是很繁琐的，有必要研究如何简化。

由于在正弦交流电路中 , 所有的电压、电流都是同频率的正弦量，所以要确定这些正弦量，只要确定它们的有效值和初相就可以了。

相量法就是用复数来表示正弦量。

使正弦交流电路的稳态分析与计算转化为复数运算的一种方法。

二、复数概述1 ．复数：形如的式子称为复数，为复数的实部，为复数的虚部，、均为实数，为虚数单位。

图 4-3 复数的图示法2 ．复数的图示法式中为复数 A 的模，为复数 A 的辐角。

3 ．复数的表示形式及其相互转换其中代数式常用于复数的加减运算，极坐标式常用于复数的乘除运算。

4 ．复数的运算法则①相等条件：实部和虚部分别相等（或模和辐角分别相等）。

②加减运算：实部和实部相加（减），虚部和虚部相加（减）。

③乘法运算：模和模相乘，辐角和辐角相加。

④ 除法运算：模和模相除，辐角和辐角相减。

三、相量表示法1 ．正弦量与复数的关系= sin( ψ )= [ ]= [ ]正弦电压等于复数函数的虚部，该复数函数包含了正弦量的三要素。

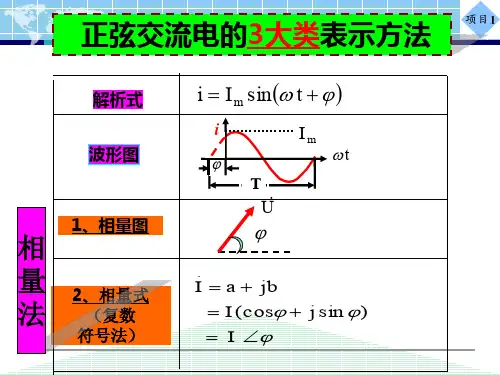
2 ．相量 ---- 分有效值相量和最大值相量① 有效值相量：= / ψ② 最大值相量：= / ψ3 ．相量图在复平面上用一条有向线段表示相量。

相量的长度是正弦量的有效值I ，相量与正实轴的夹角是正弦量的初相。

这种表示相量的图称为相量图。

例 4-4 ：。

写出表示 1 和2 的相量，画相量图。

解： 1 =100 /60 ° V2 =50 /-60 ° V相量图见图 4-4 。

例 4-5: 已知 1 =100 sin A ， 2 =100 sin( -120 ° )A ，试用相量法求 1 + 2 ，画相量图。

电工技术与电子技术—常见问题
模块五 正弦交流电路(1)
1．正弦交流电路中，有效值和最大值以及峰峰值之间有什么关系？有效值为220V 的交流电压最大值是不是380V ？
在正弦交流电路中，最大值是有效值的倍，峰峰值为最大值的2倍，也就是说
峰峰值是有效值的2倍。

有效值为220V 的交流电压其最大值为V ，也即311V 。

2. 正弦量采用相量表示时，正弦量的角频率为什么没有加以体现？
由于在采用相量表示法进行计算时，都是同频率的正弦量，所以在应用相量来表示正弦量以及画相量图的时候都是可以不用考虑正弦量的频率的。

3. 在计算交流电路时，到底采用有效值相量还是最大值相量？
两者都可以，最大值相量的模是最大值，而有效值相量的模是有效值，在计算时可以根据实际需要，如需要计算电压、电流的最大值时，可以用最大值相量，一般计算时采用有效值相量居多。

4. 正弦量的表示方法有哪些，为什么在电路计算过程中要采用相量分析法？
正弦量可以采用三角的形式以及波形图的方式来进行表示，也可以采用相量的方法来表示，由于在电路计算过程中会遇到很多正弦量的加减运算，采用相量表示法更容易进行计算，因此在正弦交流电路的计算过程中，都采用相量来表示正弦量。

5. 一个正弦量为30)V =+ﾰu t ，另外一个正弦量为
60)V =+ﾰu t ，这两个正弦量之间有没有相位差一说？
没有，相位差指的是两个同频率正弦量之间的相位之差，对于不同频率的正弦量两者比较相位差没有任何意义，因此两个不同频率的正弦量之间没有相位差一说。

正弦量相量表示1、基本概念（1）正弦电路相量表示方法。

正弦量的相量表示实质上就是用复数表示正弦量。

为与一般的复数相区别，将表示正弦量的复数称为相量。

正弦量的相量表示如表1所示。

表1正弦量的相量式三角函数式相量的极坐标式相量的直角坐标式电压tU u ωsin 2=o 0∠=U U ）（o o 0sin j 0cos +=U U 电流)30sin(2o +=t I i ωo 30∠=I I ）（o o 30sin j 0cos3+=I I电动势)30sin(2o -=t I e ωo 30-∠=E E）（o o 30sin j 0cos3-=E E （2）相量的实质与目的。

相量表示的实质上就是用复数表示正弦量。

正弦量可用三角函数式、波形图等表示，但以此方法分析正弦交流电路比较困难，引入相量的目的是为了简化正弦交流电路的分析方法，即将正弦交流电路的计算变成复数式的代数运算。

2、正弦交流电路的相量分析方法正弦交流电路引入相量后，正弦交流电路就有相量式法和相量图法两种分析方法。

（1）相量式法1）将电路中已知的正弦量电压、电流、电动势用相量表示；2）将电路中无源元件用阻抗表示，如R 、jX L 、-jX C ；3）用各种电路分析方法求解，所有方程均为相量方程。

一般加减运算用代数式；乘除运算用指数式或极坐标式。

（2）相量图法1）选取参考相量，一般并联电路选电压U 、串联电路选电流I ，复联电路要视具体情况而定；2）以参考相量为基础，根据元件上电压与电流的相位关系画出电路的相量图；3）根据相量的几何关系（平行四边形法则）求解待求物理量。

2、注意事项（1）正弦量与相量间为对应关系，不是“相等”或“等效”关系。

（2）相量法是分析计算正弦交流电路的一种辅助数学工具，可使正弦量的数学运算更为简便，且只适应于同频率的正弦量的分析计算。

（3）分析和计算正弦交流电路时，必要时可借助相量图的几何关系，同一相量图中各正弦量必须频率相同。

正弦量的相量表示法正
弦量的相量表示方法
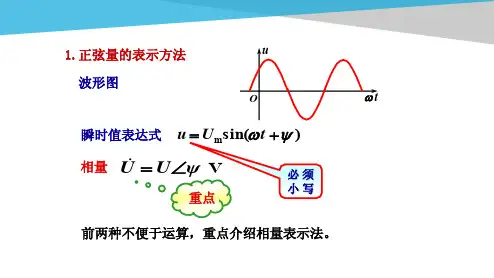
（1）正弦量的表示法
波形图、瞬时值表达式和相量的表示方法，如图1-15所示。

前两种不便于运算，重点介绍相量表示法。

（2）正弦量的旋转矢量表示法
一个正弦量的瞬时值可以用一个旋转的有向线段在纵轴上的投影值来表示称为旋转矢量。

正弦量在各时刻的瞬时值与旋转矢量在对应时刻在纵轴上的投影一一对应。

由于矢量具有了正弦量的三要素，因而正弦量可以用矢量来表示。

只有正弦量才能用矢量表示，非正弦量不可以。

只有同频率的正弦量才能画在一张矢量图上，不同频率不行。

正弦量用矢量表示时，有两种方式：若其幅度用最大值表示，则用符号
；若其幅度用有效值表示，则用符号：
正弦量矢量作图方式，如图1-16所示。

（3）正弦量的复数表示法
正弦量的复数表示方法有四种表达形式：代数形式、三角函数形式、指数形式、极坐标形式。

复数的图示，如图1-17所示。

a，b都是实数，a称为A的实部，b称为A的虚部，j=称为虚数单位（数学中用i表示，电工技术中i已用来表示电流，故改用j表示）。

②三角函数形式：
A=r（cosφ+jsinφ）
式中
③指数形式：
更多：正弦交流电的电压和电流值
百度搜索“就爱阅读”,专业资料,生活学习,尽在就爱阅读网,您的在线图书馆。

正弦量的相量表示正弦量除了采用三角函数式表示，或者用正弦波形图来表示外，还可以用相量来表示。

相量表示法的基础是复数，即用复数表示正弦量。

要将两个正弦量相加或相减时，这种方法将使计算简便而又形象。

1. 复数复数的表示形式及相互关系设复平面有一复数A ，其模为r ，幅角为ψ ，如图1所示。

它可以用以下几种形式表示；(1) 复数的代数式: b a A j +=22b a r += 复数的模ab arctan =ψ 复数的辐角(2) 复数的三角式：)sin j (cos sin j cos ψψψψ+=+=A A A A(3) 复数的指数式: ψj re A =(4) 复数的极坐标式: ψ∠=r A上述复数的四种表达形式，可以互相转换。

ψψψψ∠==+=+=r re r b a A j )sin j (cos j复数的加减运算可用代数式，复数的乘除运算可用指数式或极坐标式。

说明：数学中虚数用i 表示。

电工中在相量表示时，为了不与电流i 相混淆，改用j 表示虚数。

2．正弦量的相量表示由上可知：复数由模和幅角两个特征来确定，而正弦量由幅值、角频率、初相角三个特征来确定。

在分析线性电路时，正弦激励和响应均为同频率的正弦量，频率是已知的，可以不考虑。

因此，一个正弦量由幅值(或有效值)何初相位就可确定。

比照复数，正弦量可用复数表示。

复数的模即为正弦量的幅值(或有效值)复数的辐角即为正弦量的初相角为了与一般复数相区别，把表示正弦量的复数称相量。

用大写字母加“·”表示。

若已知正弦电压为)sin(m ψω+=t U u ，相量式可写为ψψψψ∠==+=mj m m m )sin j (cos U e U U U 最大值相量 相量的模=正弦量的最大值相量辐角=正弦量的初相角或:ψψψψ∠==+=U e U U Uj )sin j (cos 有效值相量相量的模=正弦量的有效值相量辐角=正弦量的初相角综上所述，正弦量的相量表示，其实质是将同频率的正弦量变换成它的复数形式，这样就把正弦稳态交流电路中繁琐的三角函数运算变换成复数运算，从而简化了运算过程。