10-2 平面简谐波的波函数jm
- 格式:ppt
- 大小:2.67 MB
- 文档页数:36




平面简谐波的波函数表达式
平面简谐波的波函数表达式是y=Asin(ωx+φ),其中A为振幅,2π/ω为周期,φ为初相
平面简谐波是最基本的波动形式。
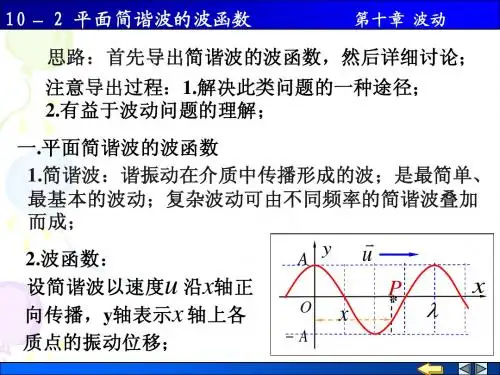
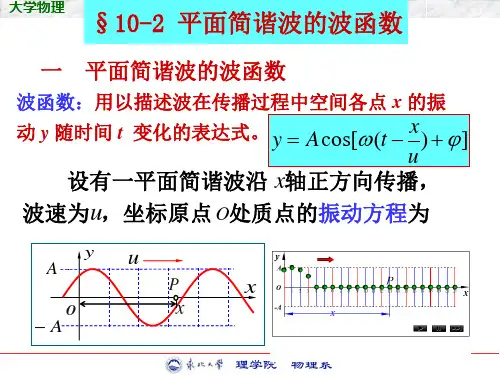
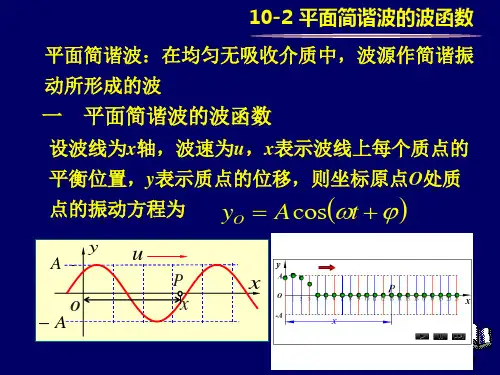
平面传播时,若介质中体元均按余弦(或正弦)规律运动,就叫平面简谐波。
如果所传播的是谐振动,且波所到之处,媒质中各质点均做同频率、同振幅的谐振动,这样的波称为简谐波,也叫余弦波或正弦波。
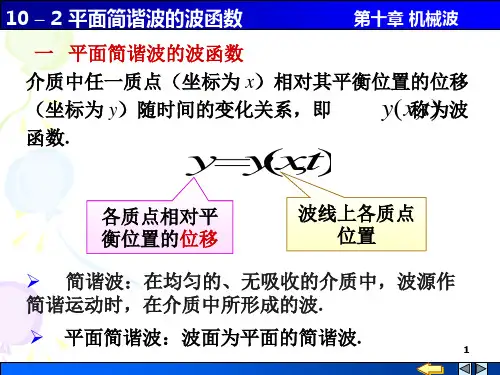
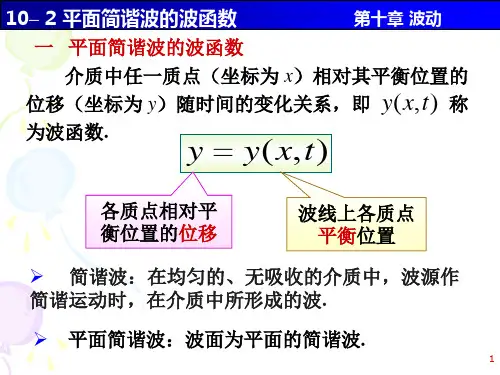
如果简谐波的波面是平面,这样的简谐波称为平面简谐波。
平面简谐波传播时,介质中各质点都作同一频率的简谐振动,但在任一时刻,各点的振动相位一般不同,它们的位移也不相同,但根据波阵面的定义知道,
在任一时刻处在同一波阵面上的各点有相同的相位,它们离开各自的平衡位置有相同的位移。
简谐平面波都往往被简称为简谐波或者平面波,后者频繁在量子力学中使用。
本书的量子力学部分也会大量使用平面波这个简称,无论波动是几维的。
广义来说,平面波未必是简谐的,只需要等相位面都是平面即可:例如波长随空间变化,频率随时间变化也仍然是平面波。
而简谐波也未必是平面的,球面波也可以在径向也是简谐函数。


平面简谐波的波函数表达式
平面简谐波是一种特殊的波形,它的波函数表达式可以用以下公式表示:
y = A sin(ωt + φ)
其中,y表示波的振幅,A表示最大振幅,ω表示角频率,t表示时间,φ表示初相位。
平面简谐波是一种具有周期性的波形,它的周期T可以用以下公式计算:
T = 2π/ω
角频率ω是一个常数,它表示单位时间内波形的变化次数。
因此,角
频率越大,波形变化的速度就越快,周期就越短。
初相位φ是一个常数,它表示波形在t=0时的相位。
不同的初相位会导致波形的相位差异,从而产生不同的波形。
平面简谐波的波函数表达式可以用于描述许多物理现象,例如声波、
电磁波等。
在声学中,平面简谐波可以用于描述声音的振动,而在电磁学中,平面简谐波可以用于描述电磁场的振动。
平面简谐波的振幅和角频率是两个重要的参数,它们可以影响波形的形状和特性。
振幅越大,波形的振动幅度就越大,而角频率越大,波形的变化速度就越快。
平面简谐波还具有一些重要的性质,例如叠加原理和相位差。
叠加原理指出,当两个或多个平面简谐波叠加在一起时,它们的振幅可以相加,从而形成一个新的波形。
相位差指出,当两个平面简谐波的相位差为0时,它们的振幅可以相加,而当相位差为π时,它们的振幅可以相消。
总之,平面简谐波是一种重要的波形,它的波函数表达式可以用于描述许多物理现象。
了解平面简谐波的特性和性质,可以帮助我们更好地理解和应用它们。
平面简谐波的波函数表达式1. 引言平面简谐波是物理学中常见的一种波动现象,它可以描述许多自然界中的振动和波动现象,如弹簧振子、光的传播等。
在量子力学中,平面简谐波也是描述粒子行为的重要工具。
本文将详细解释平面简谐波的波函数表达式,包括函数的定义、用途和工作方式等。
2. 平面简谐波的定义平面简谐波是指在空间中沿一个方向传播且振幅保持不变的一种波动现象。
它可以用一个复数函数来表示,该函数称为平面简谐波的波函数。
平面简谐波通常由以下形式表示:Ψ(x,t)=A⋅e i(kx−ωt+ϕ)其中,•Ψ(x,t)表示平面简谐波在时刻t和位置x的振幅;•A表示振幅大小;•k是空间角频率,与波长λ之间有关系:k=2π;λ•ω是时间角频率,与周期T之间有关系:ω=2π;T•ϕ是相位常数,表示波函数在原点的相位。
3. 平面简谐波的用途平面简谐波的波函数表达式在物理学中具有广泛的应用。
下面将介绍几个典型的应用场景。
3.1 波动现象平面简谐波可以用来描述许多经典物理学中的波动现象,如声波、水波等。
对于声波而言,振幅A可以表示声音的强度,k可以表示声音在空间中传播的方向和速度,ω可以表示声音的频率,ϕ可以表示声音的相位。
因此,通过平面简谐波的波函数表达式可以准确描述和分析各种不同频率、不同振幅和不同相位的声音。
3.2 光学现象平面简谐波也可以用来描述光学现象。
根据电磁学理论,光可以看作是一种电场和磁场交替变化而形成的电磁波。
因此,在光学领域中,平面简谐波的波函数表达式被广泛应用于描述光场强度、频率、相位等特性。
通过对平面简谐波的波函数进行分析,可以研究光的传播、干涉、衍射等现象,进而推导出许多重要的光学定律和规律。
3.3 量子力学在量子力学中,平面简谐波的波函数表达式被用来描述粒子的行为。
根据量子力学理论,粒子的运动状态可以用波函数描述。
平面简谐波是量子力学中最简单的波函数形式之一,它可以用来描述粒子在空间中的概率分布和运动特性。