天津市耀华嘉诚国际中学2019-2020学年八年级下学期线上学习阶段性评估检测语文试题(PDF版)

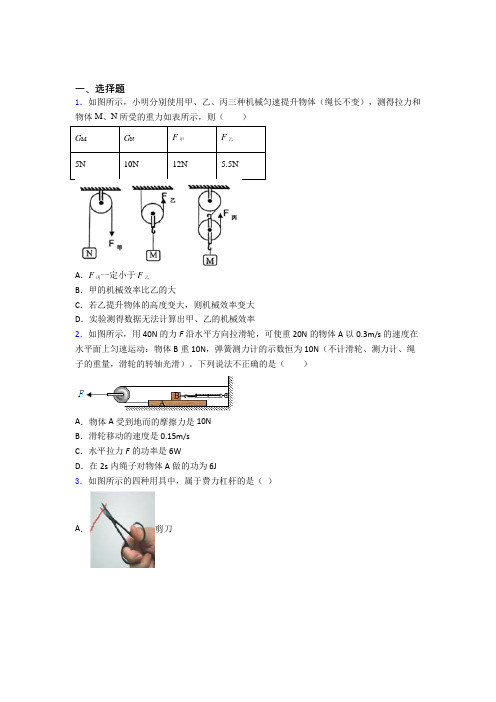
一、选择题1．如图所示，小明分别使用甲、乙、丙三种机械匀速提升物体（绳长不变），测得拉力和物体M、N所受的重力如表所示，则（）G M G N F甲F乙5N10N12N 5.5NA．F丙一定小于F乙B．甲的机械效率比乙的大C．若乙提升物体的高度变大，则机械效率变大D．实验测得数据无法计算出甲、乙的机械效率2．如图所示，用40N的力F沿水平方向拉滑轮，可使重20N的物体A以0.3m/s的速度在水平面上匀速运动：物体B重10N，弹簧测力计的示数恒为10N（不计滑轮、测力计、绳子的重量，滑轮的转轴光滑）。

下列说法不正确的是（）A．物体A受到地而的摩擦力是10NB．滑轮移动的速度是0.15m/sC．水平拉力F的功率是6WD．在2s内绳子对物体A做的功为6J3．如图所示的四种用具中，属于费力杠杆的是（）A．剪刀B．核桃钳C．钢丝钳D．面包夹子4．我们经常看到洒水车在公路上洒水作业，关于洒水车在水平公路上匀速前进洒水作业的过程中，说法正确的是（）A．动能变小，机械能变小B．动能不变，机械能不变C．动能变小，机械能不变D．动能不变，机械能变小5．下列情况下，小桂对物理课本做了功的是（）A．阅读静止在桌面上的物理课本B．水平推物理课本，但未推动C．物理课本自由下落的过程D．将物理课本从地面捡起的过程6．如图所示，完全相同的甲、乙两个小球，甲球由轻绳系住，乙球由橡皮条系住，都从水平位置由静止开始释放，当两球到达悬点正下方K点时，橡皮条长度恰好与绳子长相等，则在K点时，下列说法错误的是（）[不计空气阻力]A．v甲＞v乙B．从静止运动到K点，甲的重力做功多C．甲的动能大于乙的动能D．甲和乙的重力势能相等7．有一个模型船漂浮在一盆水上，现把其整体移至月球上。

已知月球的引力是地球的六分之一，则船所受的重力和其排开水的体积与原来相比，下列说法正确的是（）A．重力不变，排开水的体积也不变B．重力不变，排开水的体积减小C．重力减小，排开水的体积不变D．重力减小，排开水的体积也减小8．一个浸没在水中的正方体物块，其下表面受到的水对它的向上压力为20N，上表面受到水对它的向下的压力为12N，则正方体在水中受到的浮力大小和方向为()A．32N竖直向上B．8N竖直向上C．8N竖直向下D．无法判断9．与沉在水底的生汤圆相比较，漂浮在水面的熟汤圆（）A．密度小，受到的浮力等于重力B．密度大，受到的重力大于浮力C．密度相同，受到浮力大于重力D．密度相同，受到浮力等于重力10．关于力的知识，下列说法错误的是（）A．船员向后划水船就前进，这说明力的作用是相互的B．做匀速圆周运动的物体，它的运动状态发生改变C．物体对地面压力的大小始终等于物体的重力D．用相同的力击打球的不同部位，球的旋转方向不同，表明力的作用效果与力的作用点有关11．如图，把小车放在光滑的水平桌面上，向挂在小车两端的托盘里加砝码。

天津耀华嘉诚中学物理八年级下册期末试卷含答案一、选择题1．下列表述中，符合生活实际的是（）A．托起两个鸡蛋所用的力约是1NB．洗澡水的温度约是85℃C．成人步行速度一般约是5m/sD．我们用的物理课本长约是5dm2．起重机臂下吊一个重为5×104N的重物，下列情况中钢丝绳对重物的拉力T为（）A．重物静止时，T＝0NB．重物匀速上升时，T＞5×104NC．重物匀速下降时，T＜5×104ND．以上三种情况下，T都等于5×104N3．如图所示，关闭动力拉下制动后，某满载旅客的高铁沿平直轨道缓缓驶入南阳东站。

下列说法正确（）A．列车受到的重力和铁轨对它的支持力是一对平衡力B．列车由运动变为静止，列车的惯性减小了C．列车减速前进时，坐在列车上的乘客相对于车站是静止的D．列车由运动变为静止，说明物体的运动要靠力来维持4．如图所示的实例中，属于增大压强的是（）A．图钉帽做得很大B．喝饮料的管一端很尖C．铁轨下的枕木D．滑雪用的雪橇5．小明在饮料吸管中塞入一些细铁丝作为配重，并将一端封闭，制作了一只简易密度计；将其先后放入甲、乙两杯液体中，当密度计静止时，两杯中液体深度相同，如图所示，下列说法正确的是（）A．密度计在甲杯液体中受到的浮力更大B．密度计的刻度线，越往上标注的密度值越大C．密度计放入后，乙杯中液体对容器底的压强更大D．适当减小配重，可以增大该密度计两条刻度线之间的距离，使测量结果更精确6．如图所示，有一质量不计的轻质木板，木板上放有一个可连续改变重力的物块，木板左端可绕固定点O转动，右端用竖直向上的拉力F拉住使其始终在水平位置保持平衡。

当物块向左匀速滑动的过程中，若要保持拉力F大小不变，则物块的重力应该（）A．始终不变B．一直变大C．一直变小D．先变大后变小7．在水平桌面上，有甲、乙两个完全相同的烧杯，甲、乙两杯中盐水的密度分别为甲和乙。

把同一个鸡蛋分别放入甲、乙两杯盐水中，鸡蛋在甲杯中漂浮在盐水表面，而在乙杯中却悬浮在盐水中，经测量放入鸡蛋后甲、乙两杯中液面高度相同，如图所示，鸡蛋在甲、乙两杯中所受盐水压力的合力分别为F甲和F乙，鸡蛋所受的浮力分别为'F甲和'F乙，盐水对杯底的压强分别为p甲和p乙。

天津市耀华中学2020-2021学年八年级下学期期中形成性检测数学试卷学校:___________姓名：___________班级：___________考号：___________一、单选题1x 的取值范围是（ ）A ．3x ≥B ．3x >C ．3x ≥-D ．3x ≤-2 ）A ．0.5BC D3的值在（ ）A ．2到3之间B ．3到4之间C ．4到5之间D ．5到6之间4．下列算式：（1=（2）（37；（4） ） A ．（1）和（3） B ．（2）和（4） C ．（3）和（4） D ．（1）和（4） 5．利用勾股定理，可以作出长为无理数的线段．如图，在数轴上找到点A ，使OA =5，过点A 作直线l 垂直于OA ，在1上取点B ，使AB =2，以原点O 为圆心，以OB 长为半径作弧，弧与数轴的交点为C ，那么点C 表示的无理数是（ ）AB C ．7 D ．29 6．下列命题中正确的是（ ）A ．如果a ，b ，c 是一组勾股数，那么4a ，4b ，4c 也是一组勾股数B ．如果一个三角形的三个内角的度数之比是1：2：3，那么这个三角形三个内角所对的边之比也是1：2：3C ．如果直角三角形的两边分别是3，4，那么斜边一定是5D ．任何一个定理都有逆定理7．已知菱形的两条对角线的长分别是6和8，则菱形的面积是（ ）A ．48B ．40C ．24D ．208．正方形的边长为cm a ，它的面积与长为96cm ，宽为12cm 的矩形的面积相等，则a 的值为（ ）A ．B ．36C ．D ．249．如图，已知▭ABCD ，则下列结论中不正确的是（ ）A ．当AB ＝BC 时，▭ABCD 是菱形B ．当AC ⊥BD 时，▭ABCD 是菱形C ．当⊥ABC ＝90°时，▭ABCD 是矩形D ．当AC =BD 时，▭ABCD 是正方形10．我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形，任意平行四边形的中点四边形（ ）A ．平行四边形B ．矩形C ．菱形D ．正方形 11．如图，四边形ABCD 是平行四边形，过点A 作AM ⊥BC 于点M ，交BD 于点E ，过点C 作CN ⊥AD 于点N ，交BD 于点F ，连接CE ，当EA =EC ，且点M 为BC 的中点时，AB ：AE 的值为（ ）A ．2BC ．32 D12．如图，将边长为8cm 的正方形ABCD 折叠，使点D 落在BC 边的中点E 处，点A 落在点F 处，折痕为MN ，则折痕MN 的长是（ ）A ．B ．C ．cmD ．二、填空题13=______．14．“同旁内角互补，两直线平行”的逆命题是_____________________________. 15．若一个直角三角形的两直角边长分别为6和8，则其斜边上的高为________． 16．如图，网格中的小正方形边长均为1，ABC 的三个顶点在格点上，则ABC 中AB 边上的高为____．17．如图，在边长为2的菱形ABCD 中，⊥A ＝60°，M 是边AD 的中点，则CM 的长＝_____．18．如图，ABE △是等边三角形，M 是正方形ABCD 对角线BD （不含B 点）上任意一点，BM BN =，15ABN ∠=︒（点N 在AB 的左侧），当AM +BM +CM 的最小值为1时，正方形的边长为______．三、解答题19．计算：(2)- 20．如图，四边形ABCD 是矩形纸片，10AD =，8CD =，在CD 上取一点E ，将纸片沿AE 翻折，使点D 落在BC 边上的点F 处．(1)AF 的长=______；(2)BF 的长=______；(3)CF 的长=______；(4)求DE 的长．21．已知：点D ，E 分别是⊥ABC 的BC ，AC 边的中点.(1)如图⊥，若AB=10，求DE 的长；(2)如图⊥,点F 是AB 边上的一点,FG//AD,交ED 的延长线于点G.求证：AF=DG22．如图，在平行四边形ABCD 中，对角线AC ，BD 相交于点 O ，且OA=OD ，⊥OAD=50°．求⊥OAB 的度数．23．如图，在平行四边形ABCD 中，E 、F 是对角线AC 所在直线上的两点，且AE =CF ．求证：四边形 EBFD 是平行四边形．24．如图，在平面直角坐标系中，有一矩形OABC ，8OA =,6OC =，过点()0,6D 作y 轴的垂线交OA 于点E ，点B 恰在这条直线上．(1)求矩形OABC 的对角线的长；(2)求点B 的坐标；(3)求EOB △的面积．25．如图，P 为正方形ABCD 的边BC 上的一动点（P 不与B 、C 重合），连接AP ，过点B 作BQ ⊥AP 交CD 于点Q ，将BCQ △沿着BQ 所在直线翻折得到BQE △，延长QE 交BA 的延长线于点M ．(1)探求AP 与BQ 的数量关系；(2)若3AB =，2BP PC =，求QM 的长．参考答案：1．C【解析】【分析】直接利用二次根式中的被开方数是非负数，求出答案即可．【详解】解：⊥30x +≥，⊥-3x ≥，故选：C【点睛】本题考查二次根式有意义，解题的关键是正确理解二次根式有意义的条件，本题属于基础题型．2．C【解析】【分析】先把根式下的小数转化为分数的形式，再转化为最简二次根式即可．【详解】根据二次根式的性质进行化简即可．【解答】===故选：C【点睛】本题主要考查了最简二次根式的化简运算，熟悉掌握最简二次根式的概念是解题的关键． 3．B【解析】【分析】利用”夹逼法“的范围.【详解】⊥4 ＜6 ＜9 ，<，23⊥34<<，故选B.4．B【解析】【分析】根据二次根式的性质和二次根式的加法运算，分别进行判断，即可得到答案．【详解】（1（2）（3（4）==故选：B．【点睛】本题考查了二次根式的加法运算，二次根式的性质，解题的关键是熟练掌握运算法则进行解题．5．B【解析】【分析】利用勾股定理列式求出OB判断即可．【详解】解：由勾股定理得，OB⊥点C故选：B．【点睛】本题考查了勾股定理，熟记定理并求出OB 的长是解题的关键．6．A【解析】【分析】根据勾股数的定义、三角形的性质、勾股定理等知识分别判断后即可确定正确的选项．【详解】解：A 、因为a ，b ，c 是一组勾股数，所以4a ，4b ，4c 也是一组勾股数，则是真命题，故本选项符合题意；B 、设这一个三角形的三个内角的度数分别为,2,3x x x ，因为23180x x x ++=︒，则30x =︒ ，即这一个三角形的三个内角的度数分别为30,60,90︒︒︒ ，即该三角形为直角三角形，设最短边长为m ，则斜边长为2m = ，所以这个三角形三个内角所对的边之比2 ，则是假命题，故本选项不符合题意；C 、4也可能为斜边，则是假命题，故本选项不符合题意；D 、任何一个命题都有逆命题，但一个定理不一定有逆定理，则是假命题，故本选项不符合题意；故选：A【点睛】考查了命题与定理的知识，解题的关键是了解勾股数的定义、三角形的性质、勾股定理等知识，属于基础题，比较简单．7．C【解析】 【分析】根据菱形的性质，对角线互相垂直，则菱形的面积等于对角线乘积的一半，即可求得的【详解】根据题意，168242S =⨯⨯=故选C【点睛】本题考查了菱形的性质，理解菱形的性质是解题的关键．8．C【分析】根据面积公式和算术平方根的定义求解．【详解】解：由题意得a2=96×12，⊥a=，故选C．【点睛】本题考查了算术平方根，熟练掌握算术平方根的定义是解答本题的关键，正数有一个正的算术平方根，0的平方根是0，负数没有算术平方根．9．D【解析】【分析】根据菱形、矩形、正方形的判定进行逐一判定即可．【详解】解：A.当AB＝BC时，▭ABCD是菱形，一组邻边相等的平行四边形是菱形，选项说法正确，不符合题意；B. 当AC⊥BD时，▭ABCD是菱形，对角线互相垂直的平行四边形是菱形，选项说法正确，不符合题意；C. 当⊥ABC＝90°时，▭ABCD是矩形，有一个角是直角的平行四边形是矩形，选项说法正确，不符合题意；D. 当AC=BD时，▭ABCD是矩形，对角线相等的平行四边形是矩形，选项说法错误，符合题意；故选：D．【点睛】本题考查了菱形、矩形、正方形的判定，熟练掌握特殊平行四边形的判定定理是解题的关键．10．A【解析】分析：根据三角形的中位线的性质，证明对边平行且相等，由此可得到平行四边形.详解：如图,四边形ABCD中,E,N,M,F分别是DA,AB,BC,DC的中点,连接AC,DB,根据三角形中位线定理可得:EF平行且等于AC的一半,MN平行且等于AC的一半,根据平行四边形的判定可知四边形MNEF为平行四边形.故选A.点睛：此题主要考查了三角形的中位线定理，关键是利用三角形的中位线平行且等于第三边的一半，证明对边平行且相等的四边形是平行四边形.11．B【解析】【分析】根据平行四边形的性质、垂直的定义、平行线的判定定理可以推知AE⊥CF；然后由全等三角形的判定定理ASA推知⊥ADE⊥⊥CBF；最后根据全等三角形的对应边相等知AE=CF，所以对边平行且相等的四边形是平行四边形；连接AC交BF于点O，根据EA=EC推知▱ABCD是菱形，根据菱形的邻边相等知AB=BC；然后结合已知条件“M是BC的中点，AM⊥BC”证得⊥ADE⊥⊥CBF（ASA），所以AE=CF，从而证得⊥ABC是正三角形；最后在Rt⊥BCF中，求得CF：BC AE=CF，AB=BC）AB：AE【详解】解：连接AC，⊥四边形ABCD是平行四边形，⊥BC⊥AD；⊥⊥ADE =⊥CBD ，⊥AD =BC ，在⊥ADE 和⊥CBF 中，90DAE BCF AD CB ADE FBC ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩， ⊥⊥ADE ⊥⊥CBF （ASA ），⊥AE =CF ，又⊥AM ⊥BC ，⊥AM ⊥AD ；⊥CN ⊥AD ，⊥AM ⊥CN ，⊥AE ⊥CF ；⊥四边形AECF 为平行四边形，⊥EA =EC ，⊥▱AECF 是菱形，⊥AC ⊥BD ，⊥平行四边形ABCD 是菱形，⊥AB =BC ，⊥M 是BC 的中点，AM ⊥BC ，⊥AB =AC ，⊥⊥ABC 为等边三角形，⊥⊥ABC =60°，⊥CBD =30°；在Rt ⊥BCF 中，CF ：BC又⊥AE =CF ，AB =BC ，⊥AB ：AE故选：B ．【点睛】本题综合考查了全等三角形的判定与性质、菱形的判定与性质以及等边三角形的判定与性质等知识点，证得▱ABCD 是菱形是解题的难点．12．D【解析】【分析】连接DE ，因为点D 是中点，所以CE 等于4，根据勾股定理可以求出DE 的长，过点M 作MG ⊥CD 于点G ，则由题意可知MG ＝BC ＝CD ，证明⊥MNG ⊥⊥DEC ，可以得到DE =MN ，即可解决本题．【详解】解：如图，连接DE ．由题意，在Rt⊥DCE 中，CE ＝4cm ，CD ＝8cm ，由勾股定理得：DE．过点M 作MG ⊥CD 于点G ，则由题意可知MG ＝BC ＝CD ．连接DE ，交MG 于点I ．由折叠可知，DE ⊥MN ，⊥⊥NMG +MIE ＝90°，⊥⊥DIG +⊥EDC ＝90°，⊥MIE ＝⊥DIG （对顶角相等），⊥⊥NMG ＝⊥EDC ．在⊥MNG 与⊥DEC 中，90NMG EDC MG CDMGN DCE ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩⊥⊥MNG ⊥⊥DEC （ASA ）．⊥MN ＝DE＝．故选D ．【点睛】本题主要考查了正方形的性质、折叠以及全等三角形，能够合理的作出辅助线并找出全等的条件是解决本题的关键．13．3【解析】【分析】根据算术平方根的定义求解即可．【详解】3=，故答案为：3．【点睛】本题考查了算术平方根，熟练掌握算术平方根的定义是解答本题的关键， 正数有一个正的算术平方根，0的平方根是0，负数没有算术平方根．14．两直线平行，同旁内角互补【解析】【详解】分析：把一个命题的条件和结论互换就得到它的逆命题．命题“同旁内角互补，两直线平行”的条件是同旁内角互补，结论是两直线平行，故其逆命题是两直线平行，同旁内角互补．详解：命题“同旁内角互补，两直线平行”的逆命题是：两直线平行，同旁内角互补，故答案为两直线平行，同旁内角互补．点睛：考查了互逆命题的知识及命题的真假判断，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题．15．245【解析】【分析】10=，根据面积不变，得斜边上的高为16821102⨯⨯⨯，计算求【详解】10=根据面积不变，得斜边上的高为16824 215102⨯⨯=⨯故答案为：245．【点睛】本题考查了勾股定理，等面积法求三角形的高．解题的关键在于正确的计算．16【解析】【分析】由已知可得到三角形各边的长，从而根据勾股定理可求得BC边上的高，再根据面积公式即可求得AB边上的高的长．【详解】解：由图知，⊥ABC是等腰三角形，过点C作CD⊥AB于点D，⊥AB=AC=BC，⊥BC边上的高为=设CD=h，⊥S△ABC=1122=，⊥h17【解析】过点M ，作ME ⊥DE ，交CD 延长线于点E ，由菱形的性质和勾股定理易求DE 和MEA 的长，进而在直角三角形MEC 中，利用勾股定理可求出CM 的长．【详解】过点M 作ME ⊥DE ，交CD 延长线于点E ，⊥在边长为2的菱形ABCD 中，⊥A ＝60°，⊥AD ＝DC ＝2，⊥ADC ＝120°，⊥⊥ADE ＝60°，⊥M 是边AD 的中点，⊥DM ＝1，⊥DE ＝12，⊥EM⊥CM=【点睛】本题考查了菱形的性质以及勾股定理的运用，熟记菱形的各种性质是解题的关键．18【解析】【分析】首先通过SAS 判定AMB ENB △≌△，得出AM EN =，因为60ABD ABN ∠+∠=︒,BM BN =,得出MNB 是等边三角形，AM +BM +CM =EN +MN +CM ，而且为最小值，我们可以得出EC =1，作辅助线，过点E 作EF BC ⊥交CB 的延长线于F ，由题意求出30EBF ∠=︒，设正方形的边长为x ，在t R EFC △．【详解】⊥ABE △为正三角形，⊥60ABE ∠=︒，AB BE =⊥45NBE ABE ABN ∠=∠-∠=︒⊥BD 是正方形ABCD 的对角线，⊥45ABD ∠=︒⊥ABD NBE ∠=∠．在AMB 和ENB △中BM BN MBA NBE AB EB =⎧⎪∠=∠⎨⎪=⎩，⊥AMB ENB △≌△（SAS ）⊥AM EN =在MBN △中，60ABD ABN ∠+∠=︒又⊥BM BN =，⊥MBN △为等边三角形，⊥MN BM =．⊥AM +BM +CM1．⊥EN +MN +CM1即CE1．过点E 作EF BC ⊥交CB 的延长线于F ，可得906030EBF ∠=︒-︒=︒．设正方形的边长为x ，则BFx ，2x EF =． 在t R EFC △，⊥222EF FC EC +=，⊥222())1)2x x x ++=解得x =．⊥【点睛】本题考查了等边三角形和正方形边相等的性质，全等三角形的判定，灵活使用辅助线，掌握直角三角的性质，熟练运用勾股定理是解题的关键．19．（1）15；（2 【解析】【分析】(1)把被开方数相乘或相除，在化成最简二次根式或整式即可；(2)先化成最简二次根式，同时去括号，再合并同类二次根式即可．【详解】解：（1==15.（2）-=【点睛】本题考查了二次根式的混合运算的应用，熟练掌握法则是解题的关键．20．(1)10(2)6(3)4(4)5【解析】【分析】（1）根据折叠的性质即可得；（2）先根据矩形的性质可得,,90108A AB CD C B D B ===∠==︒，再根据折叠的性质可得10AF AD ==，然后在Rt ABF 中，利用勾股定理即可得；（3）根据CF BC BF =-即可得；（4）先根据折叠的性质可得EF DE =，设EF DE x ==，则8CE CD DE x =-=-，再在Rt CEF 中，利用勾股定理即可得．(1)解：由折叠的性质得：10AF AD ==，故答案为：10．(2) 解：四边形ABCD 是矩形，10AD =，8CD =，8,9010,A AB C C B D D B ∴===∠==︒，由折叠的性质得：10AF AD ==，6BF ∴==，故答案为：6．(3)解：10,6BC BF ==，1064CF BC BF ∴=-=-=，故答案为：4．(4)解：由折叠的性质得：EF DE =，四边形ABCD 是矩形，90C ∴∠=︒，设EF DE x ==，则8CE CD DE x =-=-，在Rt CEF 中，222EF CE CF =+，即222(8)4x x =-+，解得5x =，即DE 的长为5．【点睛】本题考查了矩形与折叠问题、勾股定理等知识点，熟练掌握矩形与折叠的性质是解题关键．21．（1）DE=5；（2）证明见解析.【分析】（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得DE⊥AB，DE=12AB，然后代入数据计算即可得解；（2）判断出四边形AFGD是平行四边形，再根据平行四边形的对边相等证明．【详解】（1）⊥D、E分别为BC、AC边的中点，⊥DE是△ABC的中位线，⊥DE//AB，DE=12 AB，⊥AB=10，⊥DE=5.（2）⊥F是AB边上一点，由（1）知AB//DE，⊥AF//DE，⊥FG//AD，⊥四边形AFGD为平行四边形，⊥AF=DG.【点睛】本题考查了三角形的中位线平行于第三边并且等于第三边的一半，平行四边形的判定与性质，熟记定理是解题的关键．22．40°【解析】【分析】先证四边形ABCD是矩形，根据矩形的性质求出⊥DAB，代入⊥OAB=⊥DAB-⊥OAD求出即可．解：⊥四边形ABCD是平行四边形，⊥OA=12AC,OD=12BD又⊥OA=OD⊥AC=BD⊥四边形ABCD是矩形，⊥⊥DAB=90°，⊥⊥OAD=50°，⊥⊥OAB=⊥DAB-⊥OAD=40°【点睛】本题考查了矩形的性质，能根据矩形的性质求出⊥DAB的度数是解此题的关键．23．见解析【解析】【分析】连接BD交AC于点O，根据对角线互相平分的四边形是平行四边形，可证四边形EBFD是平行四边形．【详解】解：证明：如图，连接BD交AC于点O，⊥四边形ABCD是平行四边形，⊥OA=OC，OB=OD，又⊥AE=CF，⊥OA-AE=OC-CF，即OE=OF，⊥四边形EBFD是平行四边形．【点睛】此题主要考查平行四边形的判定，熟练掌握平行四边形的判定是解题的关键． 24．(1)10(2)()8,6 (3)754【解析】【分析】(1)由矩形的性质得出AB =OC =6，⊥A =90°，由勾股定理求出OB 即可；(2)由勾股定理求出BD ，即可得出结果；(3)由AAS 证明⊥DEO ⊥⊥AEB ，得出OE =BE ，设OE=BE=x ，则DE =8-x ，在Rt ⊥ODE 中，由勾股定理求出BE ，再由三角形面积公式即可得出结果．(1)解：⊥四边形OABC 是矩形，⊥6AB OC ==，90A ∠=︒．在Rt OAB 中，由勾股定理可知：10OB ==．(2)解：⊥BD y ⊥轴，⊥在Rt BDO △中，由勾股定理可知：8DB =．⊥点B 的坐标为()8,6．(3)解：⊥6DO =，6AB =，⊥DO AB =，⊥90ODE BAE ∠=∠=︒，DEO AEB ∠=∠，⊥()DEO AEB AAS ≌△△，⊥OE BE =．设OE BE x ==，则8DE DB BE x =-=-，在Rt DOE 中，由勾股定理可知：222OD DE OE +=，代入数据：得到：()22268x x +-=， 解得254x =． ⊥25BE 4=， ⊥11257562244EOB S BE OD =⋅=⨯⨯=△． 【点睛】 本题考查了矩形的性质、勾股定理、坐标与图形性质、全等三角形的判定与性质；第(3)问中得到证明BE =OE ，由勾股定理求出BE 的长是解题的关键．25．(1)AP BQ = (2)134【解析】【分析】（1）只需要证出()PBA QCB ASA ≌，即可解题．（2）过点Q 作QH AB ⊥于点H ，易得QH =BC =AB =3，BP =2，PC =1运用勾股定理可以求得AP ，又因为DC //AB ，可得CQB QBA ∠=∠，由折叠知识得EQB CQB ∠=∠，所以QBA EQB ∠=∠，可得MQ =MB ．通过设定未知数，在t R MHQ 中我们通过勾股定理就可以解决问题．(1)⊥四边形ABCD 是正方形，⊥AB =BC ，⊥90ABQ CBQ ∠+∠=︒，⊥BQ ⊥AP⊥90PAB QBA ∠+∠=︒，⊥PAB CBQ ∠=∠，在PBA △和BCQ △中，{PAB CBQAB BC ABP BCQ∠=∠=∠=，⊥()PBA QCB ASA ≌，⊥AP BQ =．(2)过点Q 作QH AB ⊥于H ，如图⊥四边形ABCD 是正方形，⊥QH =BC =AB =3，⊥BP =2PC ，⊥BP =2，PC =1，⊥BQ AP ==⊥2BH ===，⊥四边形ABCD 是正方形，⊥DC //AB⊥CQB QBA ∠=∠，由折叠知识得EQB CQB ∠=∠，⊥QBA EQB ∠=∠，⊥MQ =MB ，设QM =x ，则有MB =x ，MH =x -2，在t R MHQ 中，根据勾股定理可得222(2)3x x =-+，解得x =134， ⊥QM 的长为134． 【点睛】 本题主要考查了正方形的性质，全等三角形的判定和性质，勾股定理，折叠之后完全相同，包括边的长度还有角的度数完全相等，再设未知数，然后运用勾股定理建立方程，这是求线段长度最常用的方法．。

天津耀华嘉诚国际中学物理八年级下册期末试卷含答案一、选择题1．下面是对日常生活中一些数据的估计，其中最接近实际的是（）A．一名中学生所受的重力约为120N B．初中物理教科书的质量约0.12kgC．人的正常步行速度约12m/s D．雪峰山山顶的大气压大约是1.2×105Pa 2．下列关于力和运动的说法中正确的是（）A．人用力推车，车未动，是因为推力小于摩擦力B．苹果在空中下落得越来越快，是因为力可以改变物体的运动状态C．汽车关闭发动机后，速度减小最后停下来，是因为汽车不再受牵引力作用D．百米赛跑运动员冲线后不能立即停下来，是因为运动员受到惯性力的作用3．一个物体在空中由静止竖直下落，在下落过程中（不计空气阻力），假设物体突然失去重力，那么物体将（）A．立即停止运动B．速度越来越慢，最后停止运动C．以失去重力时刻的速度继续下落，做匀速直线运动D．继续下落，速度越来越大4．下列现象中利用了大气压强的是（）A．雪橇做的比较宽大B．拦河坝做的下宽上窄C．用吸管喝饮料D．刀口磨的很锋利5．如图、体积相同的两物体A、B用不可伸长的细线系住，放入水中后，A有五分之一体积露出水面，细线被拉直。

已知A重4N，B受到的浮力为10N，A、B密度之比为1:5，以下说法正确的是（）A．A、B所受的重力之比为5:1B．A、B所受的浮力之比为1:5C．细线对A的拉力大小为6N D．B对容器底部的压力为6N6．如图所示，下列工具在使用时属于省力杠杆的是（）A．扫帚B．瓶盖起子C．钓鱼竿D．筷子7．如图所示，在三个相同的容器中装有质量相同的水，将木块A、金属块B按不同的方式放入水中，待A、B静止时，三个容器的底部所受的水的压强相比较，正确的是（）A．p甲>p乙>p丙B．p甲=p乙>p丙C．p甲<p乙<p丙D．p甲<p乙=p丙8．如图所示，粗糙的弧形轨道竖直固定于水平面，一小球由A点以速度ν沿轨道滚下，经另一侧等高点B后到达最高点C．下列关于小球滚动过程的分析正确的是（）A．整个过程只有重力在对小球做功B．小球在A、B两点具有的动能相同C．小球在A、B、C三点的速度大小关系是νA＞νB＞νCD．小球在A点具有的机械能等于它在C点具有的重力势能二、填空题9．如图所示是小华和小红合作做的两个力学实验，其中主要说明力可以改变物体运动状态的是_____图，主要说明力可以改变物体形状的是______图（以上均选填“甲”或“乙”）。

一、选择题1．某校九年级（1）班部分学生上学路上所花时间如图所示．设他们上学路上所花时间的平均数为a ，中位数为b ，众数为c ，则有（ ）A ．b a c >>B ．c a b >>C ．a b c >>D ．b c a >> 2．反映一组数据变化范围的是（ ）A ．极差B ．方差C ．众数D ．平均数3．小亮同学想知道自己的体重在班级中是否属于中等水平，则需了解全班同学体重的（ ） A ．平均数B ．中位数C ．众数D ．极差4．在我县“我的中国梦”演讲比赛中，有7名同学参加了比赛，他们最终决赛的成绩各不相同．其中一名学生想要知道自己是否进入前3名，不仅要知道自己的分数，还得知道这7名学生成绩的（ ） A ．众数B ．方差C ．平均数D ．中位数5．下面说法正确的个数有（ ）（1）二元一次方程组的两个方程的所有解，叫做二元一次方程组的解； （2）如果a b >，则ac bc >；（3）三角形的外角等于与它不相邻的两个内角的和； （4）多边形内角和等于360︒； （5）一组数据1，2，3，4，5的众数是0 A ．0个B ．1个C ．2个D ．3个6．2017年世界未来委员会与联合国防治荒漠化公约授予我国“未来政策奖”，以表彰我国在防治土地荒漠化方面的突出成就．如图是我国荒漠化土地面积统计图，则荒漠化土地面积是五次统计数据的中位数的年份是( )A ．1999年B ．2004年C ．2009年D ．2014年7．一个射手连续射靶22次，其中3次射中10环，7次射中9环，9次射中8环，3次射中7环．则射中环数的中位数和众数分别为（）A．8.5，9 B．8.5，8 C．8，8 D．8，9=，S2乙8．某次知识竞赛中，两组学生成绩如下表，通过计算可知两组的方差为S2甲172=，下列说法：256①两组的平均数相同；②甲组学生成绩比乙组学生成绩稳定；③甲组成绩的众数>乙组成绩的众数；④两组成绩的中位数均是80，但成绩≥80的人数甲比乙组多，从中位数来看，甲组成绩总体比乙组好；⑤成绩高于或等于90分的人数乙组比甲组多，高分段乙组成绩比甲组好．其中正确的有（）个A．2 B．3 C．4 D．59．数据5，2，3，0，5的众数是( )A．0 B．3 C．6 D．510．有一组数据：1，1，1，1，m．若这组数据的方差是0，则m为（）A．4-B．1-C．0 D．111．某小组7名学生的中考体育分数如下：37，40，39，37，40，38，40，该组数据的众数、中位数分别为（）A．40，37B．40，39C．39，40D．40，3812．为了解某小区“全民健身”活动的开展情况，随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计，结果如下表：锻炼时间（时）34567人数（人）6131452这40名居民一周体育锻炼时间的众数和中位数是( )A．14,5 B．14,6 C．5,5 D．5,6第II卷（非选择题）请点击修改第II卷的文字说明参考答案二、填空题13．在学校演讲比赛中，10名选手的成绩统计图如图所示，则这10名选手成绩的平均分是____分．14．已知一组样本数据1x ，2x ，3x ，⋅⋅⋅，n x 的平均数为2，方差为3，则数据12+5x ，22+5x ，325x +，⋅⋅⋅，2+5n x 的平均数为__________，方差为__________．15．图中显示的是某商场日用品柜台10名售货员4月份完成销售额（单位：千元）的情况，根据统计图，我们可以计算出该柜台的人均销售额为___________千元．16．已知一组数据x 1，x 2，x 3，x 4，x 5的平均数是2，那么另一组数据3x 1﹣2，3x 2﹣2，3x 3﹣2，3x 4﹣2，3x 5﹣2的平均数是_____．17．某中学人数相等的甲、乙两班学生参加了同一次数学测验，两班平均分和方差分别为⎺x 甲=82分，⎺x 乙=82分，S 2甲=245，S 2乙=190．那么成绩较为整齐的是__________班 18．某班45名同学的数学平均分是80分，其中女生有20名，她们的数学平均分为82分，那么这个班男同学的数学平均分为______分.19．一组数据：3、5、8、x 、6，若这组数据的极差为6，则x 的值为__________. 20．为调查某班学生每天使用零花钱的情况，张华随机调查了30名同学，结果如下表： 每天使用零花钱（单位:元） 1 2 3 4 5 人 数25896则这30名同学每天使用的零花钱的中位数是_____元．三、解答题21．嘉淇同学利用业余时间进行射击训练，一共射击 7 次，经过统计，制成如图所示的折线统计图．（1）这组成绩的众数是 ；中位数是 ； （2）求这组成绩的方差；22．为了倡导“节约用水，从我做起”的活动，某市政府决定对市直机关500户家庭的用水情况作一次调查，调查小组随机抽查了其中100户家庭一年的月平均用水量（单位：吨）．并将调查结果制成了如图所示的条形统计图．（1）这100个样本数据的平均数是、众数是和中位数是；（2）根据样本数据，估计该市直机关500户家庭中月平均用水量不超过12吨的约有多少户？23．嘉淇同学利用业余时间进行射击训练，一共射击7次，经过统计，制成如图12所示的折线统计图．（1）这组成绩的众数是；（2）求这组成绩的方差；（3）若嘉淇再射击一次（成绩为整数环），得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数，求第8次的射击成绩的最大环数．24．某公司销售部有营销人员15人，销售部为了制定某种商品的月销售定额，统计了这15人某月的销售量如下：每人销售件数1650510250210150120人数113532（1）求这15位营销人员该月销售量的平均数、中位数和众数；（2）假设销售负责人把每位营销员的月销售额定为310件，你认为是否合理，为什么？如不合理，请你制定一个较合理的销售定额，并说明理由．25．学校为了让同学们走向操场、积极参加体育锻炼，启动了“学生阳光体育运动”，张明和李亮在体育运动中报名参加了百米训练小组．在近几次百米训练中，教练对他们两人的测试成绩进行了统计和分析，请根据图表中的信息解答以下问题：平均数中位数方差张明13.30.004李亮13.30.02（1）张明第2次的成绩为：秒；（2）张明成绩的平均数为：；李亮成绩的中位数为：；（3）现在从张明和李亮中选择一名成绩优秀的去参加比赛，若你是他们的教练，应该选择谁？请说明理由．26．山青养鸡场有2500只鸡准备对外出售．从中随机抽取了一部分鸡，统计了它们的质量（单位：kg），并绘制出如下的统计图1和图2．请根据以上信息解答下列问题：（1）图1中m的值为；（2）统计的这组数据的众数是；中位数是；（3）求出这组数据的平均数，并估计这2500只鸡的总质量约为多少kg．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】先根据图形得出相关数据，再分别求出平均数、中位数、众数，由此即可得．【详解】由图可知，统计的学生人数为43310++=（人），他们上学路上所花时间分别为20,20,20,20,30,30,30,40,40,40，则平均数202020203030304040402910a+++++++++==，中位数3030302b+==，因为20出现的次数最多，所以众数20c=，因此有b a c>>，故选：A．【点睛】本题考查了平均数、中位数、众数，熟练掌握相关定义和计算公式是解题关键．2．A解析：A【分析】根据极差是刻画数据离散程度的一个统计量．它能反映数据的波动范围大小解答．【详解】解：反映一组数据变化范围的是极差；故选：A．【点睛】本题考查了极差、方差、众数以及平均数的概念和意义，掌握极差是刻画数据离散程度的一个统计量．它能反映数据的波动范围是解题的关键．3．B解析：B【分析】根据中位数的定义进行解答即可．∵小亮同学想知道自己的体重在班级中是否属于中等水平，∴需了解全班同学体重数据的中间的数据，即中位数，故选：B．【点睛】本题主要考查统计的有关知识，中位数是一组数据中，最中间的数据；对统计量进行合理的选择和恰当的运用是解题关键．4．D解析：D【分析】由于其中一名学生想要知道自己能否进入前3名，共有7名选手参加，故应根据中位数的意义分析．【详解】由于总共有7个人，且他们的成绩各不相同，第3的成绩是中位数，要判断是否进入前3名，故应知道中位数的多少．故选：D．【点睛】此题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义．反映数据集中程度的统计量有平均数、中位数、众数、方差等，各有局限性，因此要对统计量进行合理的选择和恰当的运用．5．B解析：B【分析】利用二元一次方程组的解的定义、不等式的性质、三角形的内角的性质及众数的定义分别判断后即可确定正确的选项．【详解】解：（1）二元一次方程组的两个方程的所有公共解，叫做二元一次方程组的解，故原命题错误，不符合题意；（2）如果a＞b，则当c＜0时，ac＞bc，故原命题错误，不符合题意；（3）三角形的外角等于与它不相邻的两个内角的和，正确，符合题意；（4）多边形内角和等于（n-2）×180°，故原命题错误，不符合题意；（5）数据1，2，3，4，5没有众数，故错误，不符合题意，正确的个数为1个，故选：B．【点睛】本题考查了二元一次方程组的解的定义、不等式的性质、三角形的内角的性质及众数的定义，属于基础知识，比较简单．6．C解析：C把数据的年份从小到大排列，根据中位数的定义即可得答案，【详解】把数据的年份从小到大排列为：2014年、1994年、2009年、2004年、1999年，∵中间的年份是2009年，∴五次统计数据的中位数的年份是2009年，故选：C．【点睛】本题考查中位数，把一组数据按从小到大的数序排列，在中间的一个数字(或两个数字的平均值)叫做这组数据的中位数．7．C解析：C【分析】找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数，众数是一组数据中出现次数最多的数据，注意众数可以不止一个．【详解】这组数据中出现次数最多的一个数是8，所以这组数据的众数是8环；22是偶数，按大小顺序排列后中间两个数是8和8，所以这组数据的中位数是8（环）．故选：C．【点睛】此题考查众数和中位数．注意掌握中位数和众数的定义是解题关键．8．C解析：C【分析】根据中位数、众数、方差、平均数的概念来解答．【详解】解：①平均数：甲组：（50×2+60×5+70×10+80×13+90×14+100×6）÷50=80，乙组：（50×4+60×4+70×16+80×2+90×12+100×12）÷50=80，②S甲2=172＜S乙2=256，故甲组学生成绩比乙组学生成绩稳定；③甲组成绩的众数90＞乙组成绩的众数70；④成绩≥80的人数甲组33人比乙组26人多；从中位数来看，甲组成绩80=乙组成绩80，故错误．⑤成绩高于或等于90分的人数乙组24人比甲组20人多，高分段乙组成绩比甲组好．故①②③⑤正确．故选：C．【点睛】此题考查中位数和众数的定义．解题关键在于掌握各定义性质.9．D解析：D根据众数的概念直接求解，判定正确选项．【详解】数据5出现了2次，次数最多，所以众数是5．故选：D．【点睛】考查了众数的概念．众数是一组数据中出现次数最多的数据，注意众数可以不止一个．10．D解析：D【分析】方差：一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差．【详解】依题意可得，平均数：45mx∴224441555m mm解得m=1，故选D．【点睛】本题考查了方差，熟练运用方差公式是解题的关键．11．B解析：B【分析】根据众数和中位数的概念求解可得．【详解】将数据重新排列为37，37，38，39，40，40，40所以这组数据的众数为40，中位数为39，故选B．【点睛】本题考查了中位数和众数的概念，一组数据中出现次数最多的数据叫做众数；将一组数据按照从小到大(或从大到小)的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．12．C解析：C【解析】众数是一组数据中出现次数最多的数据，中位数是将一组数据按大小依次排列，把处在最中间位置的一个数据或者最中间两个数据的平均数叫这组数据的中位数．本组数据中，把数据按照从大到小的顺序排列，最中间的两个数的平均数即为中位数．【详解】由统计表可知：体育锻炼时间最多的是5小时，故众数是5小时；统计表中是按从小到大的顺序排列的，最中间两个人的锻炼时间都是5小时，故中位数是5小时．故选C．【点睛】本题考查了确定一组数据的众数和中位数的能力．将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数．注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数．如果数据有奇数个，则正中间的数字即为所求；如果是偶数，则找中间两位数的平均数．二、填空题13．885【分析】首先求出10名选手的总成绩再求出平均分即可【详解】解：根据统计图可知这10名选手成绩的平均分为=885（分）故答案为885【点睛】本题主要考查了加权平均数的知识掌握加权平均数的计算公式解析：88.5【分析】首先求出10名选手的总成绩，再求出平均分即可．【详解】解：根据统计图可知，这10名选手成绩的平均分为28018559029510⨯+⨯+⨯+⨯=88.5（分），故答案为88.5．【点睛】本题主要考查了加权平均数的知识，掌握加权平均数的计算公式是解题的关键．14．912【分析】利用平均数求法和方差的方法分别列式求得平均数和方差得出答案即可【详解】∵x1x2…xn的平均数为2∴x1+x2+…+xn=2n∴=2×2+5=9∵原平均数为2新数据的平均数变为9则原来解析：9 12【分析】利用平均数求法和方差的方法分别列式求得平均数和方差得出答案即可．【详解】∵x1、x2、…x n的平均数为2，∴x1+x2+…+x n=2n，∴12252525n x x x n++++⋯++ =2×2+5=9， ∵原平均数为2，新数据的平均数变为9，则原来的方差S 12=1n [（x 1-2）2+（x 2-2）2+…+（x n -2）2]=3， 现在的方差S 22=1n [（2x 1+5-9）2+（2x 2+5-9）2+…+（2x n +5-9）2] =1n[4（x 1-2）2+4（x 2-2）2+…+4（x n -2）2]=4×3=12． 故答案为：9，12．【点睛】此题考查平均数与方差的意义，掌握平均数与方差的计算方法是解题的关键．15．67【分析】首先根据题意求出销售额为5千元的人数由此进一步求出该柜台的人均销售额即可【详解】由题意得：销售额为5千元的人数为：（人）∴该柜台的人均销售额为：（千元）故答案为：【点睛】本题主要考查了平 解析：6.7【分析】首先根据题意求出销售额为5千元的人数，由此进一步求出该柜台的人均销售额即可.【详解】由题意得：销售额为5千元的人数为：1012214----=（人），∴该柜台的人均销售额为：()1324452812010 6.7⨯+⨯+⨯+⨯+⨯÷=（千元）， 故答案为：6.7.【点睛】本题主要考查了平均数的计算，熟练掌握相关概念是解题关键.16．4【解析】【分析】平均数的计算方法是求出所有数据的和然后除以数据的总个数先求数据x1x2x3x4x5的和然后再用平均数的定义求新数据的平均数【详解】一组数据x1x2x3x4x5的平均数是2有15（x解析：4【解析】【分析】平均数的计算方法是求出所有数据的和，然后除以数据的总个数．先求数据x 1，x 2，x 3，x 4，x 5的和，然后再用平均数的定义求新数据的平均数．【详解】一组数据x 1，x 2，x 3，x 4，x 5的平均数是2，有（x 1+x 2+x 3+x 4+x 5）=2，那么另一组数据3x 1-2，3x 2-2，3x 3-2，3x 4-2，3x 5-2的平均数是（3x 1-2+3x 2-2+3x 3-2+3x 4-2+3x 5-2）=4．故答案是：4．【点睛】考查的是样本平均数的求法及运用，解题关键是记熟公式：.17．乙【解析】【分析】根据方差的意义方差反映了一组数据的波动大小根据方差越小波动越小故可由两班的方差得到结论【详解】∵S2甲＞S2乙∴成绩较为稳定的是乙故答案为乙【点睛】本题考查了方差的意义：反映了一组解析：乙【解析】【分析】根据方差的意义，方差反映了一组数据的波动大小，根据方差越小，波动越小，故可由两班的方差得到结论．【详解】∵S2甲＞S2乙∴成绩较为稳定的是乙．故答案为乙．【点睛】本题考查了方差的意义：反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．18．784【解析】【分析】设男生的平均分为x分根据男生总分和女生总分的和是全体学生的总分结合全班45名同学平均分是80分其中女生有20名她们的数学平均分为82分我们可以构造出一个关于x的方程解方程即可求解析：78.4【解析】【分析】设男生的平均分为x分，根据男生总分和女生总分的和是全体学生的总分，结合全班45名同学，平均分是80分，其中女生有20名，她们的数学平均分为82分，我们可以构造出一个关于x的方程，解方程即可求出x的值．【详解】设男生的平均分为x分，x+⨯=⨯，则2582204580x=．解得78.4即这个班男同学的数学平均分为78.4分．故答案为78.4．【点睛】本题考查了加权平均数，其中根据男生总分和女生总分的和是全体学生的总分，结合已知条件，构造关于x的方程是解题的关键．19．2或9【解析】【分析】根据极差的定义先分两种情况进行讨论当x最大时或最小时分别进行求解即可【详解】∵数据358x6的极差是6∴当x最大时：x﹣3=6解得：x=9；当x最小时8﹣x=6解得：x=2∴x解析：2或 9【解析】【分析】根据极差的定义先分两种情况进行讨论，当x最大时或最小时分别进行求解即可．【详解】∵数据3、5、8、x、6的极差是6，∴当x最大时：x﹣3=6，解得：x=9；当x最小时，8﹣x=6，解得：x=2，∴x的值为2或9．故答案为：2或9．【点睛】本题考查了极差，掌握极差的定义是解题的关键；求极差的方法是用一组数据中的最大值减去最小值．20．35【解析】分析:利用众数的定义可以确定众数在第三组由于张华随机调查了20名同学根据表格数据可以知道中位数是按从小到大排序第15个与第16个数的平均数详解:∵4出现了9次它的次数最多∴众数为4∵张华解析：3.5【解析】分析: 利用众数的定义可以确定众数在第三组，由于张华随机调查了20名同学，根据表格数据可以知道中位数是按从小到大排序，第15个与第16个数的平均数．详解: ∵4出现了9次，它的次数最多，∴众数为4．∵张华随机调查了30名同学，∴根据表格数据可以知道中位数＝（3＋4）÷2＝3.5，即中位数为3.5．故答案为：3.5．点睛: 本题属于基础题，考查了确定一组数据的中位数和众数的能力．要明确定义，一些学生往往对这个概念掌握不清楚，计算方法不明确而误选其它选项，注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数．三、解答题21．（1）10，9（2）8 7【分析】（1）根据众数的定义：一组数据中出现次数最多的数和中位数的定义：按照顺序排列的一组数据中居于中间位置的数，结合统计图得到答案；（2）先求出这组数的平均数，再求出这组成绩的方差．【详解】解：（1）由折线统计图可知第1次：10环；第2次：7环；第3次：10环；第4次：10环；第5次：9环；第6次：8环；第7次：9环10出现的次数最多，所以众数为10；这7次成绩从小到大排列为：7，8，9，9，10，10，10，故中位数为9．（2）这组成绩的平均数为：()1107101098997++++++=， 这组成绩的方差为：()()()()2222181093992897977⎡⎤-⨯+-⨯+-+-=⎣⎦ 【点睛】本题考查了折线统计图，中位数，众数及方差．掌握中位数，众数及方差的定义是解题的关键．22．（1）11.6吨，11吨，11吨；（2）约有350户．【分析】（1）根据平均数的计算公式、众数与中位数的定义即可得；（2）先求出月平均用水量不超过12吨的户数占比，再乘以500即可得．【详解】（1）这100个样本数据的平均数是1020114012101320141011.6100⨯+⨯+⨯+⨯+⨯=（吨），因为11吨出现的次数最多，所以众数是11吨，由中位数的定义得：将这100个样本数据按从小到大进行排序后，第50个和第51个数据的平均数即为中位数， 则中位数是1111112+=（吨）， 故答案为：11.6吨，11吨，11吨； （2）月平均用水量不超过12吨的户数占比为204010100%70%100++⨯=， 则70%500350⨯=（户），答：500户家庭中月平均用水量不超过12吨的约有350户．【点睛】本题考查了平均数的计算公式、众数与中位数的定义、用样本估计总体，熟练掌握数据分析的相关知识是解题关键．23．（1）10；（2）87；（3）9环 【分析】（1）根据众数的定义，一组数据中出现次数最多的数，结合统计图得到答案． （2）先求这组成绩的平均数，再求这组成绩的方差；（3）先求原来7次成绩的中位数，再求第8次的射击成绩的最大环数．【详解】解：（1）在这7次射击中，10环出现的次数最多，故这组成绩的众数是10；（2）嘉淇射击成绩的平均数为：()1107101098997++++++=， 方差为：()()()()22221[109791091097-+-+-+- ()()()2228998999]7+-+-+-=. （3）原来7次成绩为7 8 9 9 10 10 10，原来7次成绩的中位数为9，当第8次射击成绩为10时，得到8次成绩的中位数为9.5，当第8次射击成绩小于10时，得到8次成绩的中位数均为9，因此第8次的射击成绩的最大环数为9环.【点睛】本题主要考查了折线统计图和众数、中位数、方差等知识．掌握众数、中位数、方差以及平均数的定义是解题的关键．24．（1）310， 210， 210；（2）不合理，理由见解析．【分析】（1）找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数，众数是一组数据中出现次数最多的数据，注意众数可以不止一个．平均数是指在一组数据中所有数据之和再除以数据的个数．（2）根据表中数据和平均数、中位数和众数的意义回答．【详解】解：（1）平均数是：1650510250321051503120231015++⨯+⨯+⨯+⨯=（件)， 表中的数据是按从大到小的顺序排列的，处于中间位置的是210，因而中位数是210（件)，210出现了5次最多，所以众数是210；（2）不合理．因为15人中有13人的销售额不到310件，310件虽是所给一组数据的平均数，它却不能很好地反映销售人员的一般水平．销售额定为210件合适些，因为210件既是中位数，又是众数，是大部分人能达到的定额．【点睛】此题考查了中位数，众数，平均数，它们都是反映数据集中趋势的指标，掌握平均数、中位数和众数的意义是解题的关键．25．（1）13.4；（2）13.3秒，13.3秒；（3）选择张明，理由见解析．【分析】（1）根据统计图给出的数据可直接得出答案；（2）利用平均数的计算公式可得出张明成绩的平均数；先将李亮的成绩按照从小到大排列，然后即可得到这组数据的中位数；（3）在平均数、中位数相同的情况下，再根据方差越小数据越稳定，即可得出答案．【详解】解：（1）根据统计图可知，张明第2次的成绩为13.4秒，故答案为：13.4；（2）张明成绩的平均数为：13.313.413.313.213.35++++=13.3（秒）；李亮的成绩是：13.2，13.4，13.1，13.5，13.3，把这些数从小到大排列为：13.1，13.2，13.3，13.4，13.5，则李亮成绩的中位数是：13.3秒；故答案为：13.3秒，13.3秒；（3）选择张明参加比赛，因为张明和李亮成绩的平均数、中位数都相同，但张明成绩的方差小于李亮成绩的方差，张明成绩比李亮成绩稳定．【点睛】本题考查了平均数，中位数，方差的意义．平均数表示一组数据的平均程度；中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）；方差是用来衡量一组数据波动大小的量．26．（1）28；（2）1.8kg，1.5kg；（3）平均数是1.52kg，总质量约为3800kg．【分析】（1）根据各种质量的百分比之和为1可得m的值；（2）根据众数、中位数、加权平均数的定义计算即可；（3）根据平均数的计算公式求出这组数据的平均数，再乘以总只数即可得出鸡的总质量．【详解】（1）图①中m的值为100﹣（32+8+10+22）＝28，故答案为：28；（2）∵1.8kg出现的次数最多，∴众数为1.8kg，把这些数从小到大排列，则中位数为1.5 1.52+＝1.5（kg）；故答案为：1.8kg，1.5kg；（3）这组数据的平均数是：151114164++++×（5×1+11×1.2+14×1.5+16×1.8+4×2），＝150⨯（5+13.2+21+28.8+8），＝1.52（kg），∴2500只鸡的总质量约为：1.52×2500＝3800（kg），所以这组数据的平均数是1.52kg，2500只鸡的总质量约为3800kg．【点睛】此题考查统计计算，正确掌握部分百分比的计算方法，众数的定义、中位数的定义，平均数的计算方法是解题的关键.。

一、选择题1．(0分)[ID ：9927]如图，四边形ABCD 是长方形，AB=3，AD=4．已知A （﹣32，﹣1），则点C 的坐标是（ ）A ．（﹣3，32）B ．（32，﹣3）C ．（3，32）D ．（32，3） 2．(0分)[ID ：9902]估计26的值在（ ）A ．2和3之间B ．3和4之间C ．4和5之间D ．5和6之间3．(0分)[ID ：9895]如图，在5×5的正方形网格中，从在格点上的点A ，B ，C ，D 中任取三点，所构成的三角形恰好是直角三角形的个数为（ ）A ．1B ．2C ．3D ．44．(0分)[ID ：9889]如图，若点P 为函数(44)y kx b x =+-≤≤图象上的一动点，m 表示点P 到原点O 的距离，则下列图象中，能表示m 与点P 的横坐标x 的函数关系的图象大致是（ ）A ．B ．C ．D ．5．(0分)[ID ：9881]如图，在正方形OABC 中，点A 的坐标是()3,1-，则C 点的坐标是( )A ．()1,3B ．()2,3C ．()3,2D ．()3,16．(0分)[ID ：9867]如图，在矩形ABCD 中，E ，F 分别是边AB ，CD 上的点，AE=CF ，连接EF ，BF ，EF 与对角线AC 交于点O ，且BE=BF ，∠BEF=2∠BAC ，FC=2，则AB 的长为（ ）A ．83B ．8C ．43D ．67．(0分)[ID ：9844]在水平地面上有一棵高9米的大树， 和一棵高4米的小树，两树之间的水平距离是12米，一只小鸟从小树的顶端飞到大树的顶端，则小鸟至少飞行( )A ．12米B ．13米C ．9米D ．17米 8．(0分)[ID ：9842]对于次函数21y x =-，下列结论错误的是( )A ．图象过点()0,1-B ．图象与x 轴的交点坐标为1(,0)2C ．图象沿y 轴向上平移1个单位长度，得到直线2y x =D ．图象经过第一、二、三象限9．(0分)[ID ：9926]如图是自动测温仪记录的图象，它反映了齐齐哈尔市的春季某天气温T 如何随时间t 的变化而变化，下列从图象中得到的信息正确的是( )A．0点时气温达到最低B．最低气温是零下4℃C．0点到14点之间气温持续上升D．最高气温是8℃10．(0分)[ID：9919]甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟，在整个步行过程中，甲、乙两人的距离y（米）与甲出发的时间t（分）之间的关系如图所示，下列结论：①甲步行的速度为60米/分；②乙走完全程用了32分钟；③乙用16分钟追上甲；④乙到达终点时，甲离终点还有300米其中正确的结论有（）A．1个B．2个C．3个D．4个11．(0分)[ID：9836]下列各式不成立的是（）A8718293=B22233+=C 818495+==D3232=+12．(0分)[ID：9834]下列运算正确的是()A532=B822=C114293=D()22525-=-13．(0分)[ID：9833]下列各式中一定是二次根式的是( )A23-B2(0.3)-C2-D x 14．(0分)[ID：9885]如图，ABC中，CD AB⊥于,D E是AC的中点．若6,5,AD DE==则CD的长等于（）A ．5B ．6C ．8D ．1015．(0分)[ID ：9925]已知一次函数y ＝﹣x +m 和y ＝2x +n 的图象都经过A （﹣4，0），且与y 轴分别交于B 、C 两点，则△ABC 的面积为（ ）A ．48B ．36C ．24D ．18二、填空题16．(0分)[ID ：10022]一组数据1，2，a 的平均数为2，另一组数据﹣1，a ，1，2，b 的唯一众数为﹣l ，则数据﹣1，a ，1，2，b 的中位数为 _________． 17．(0分)[ID ：10021]比较大小：52_____13． 18．(0分)[ID ：10017]计算：2(21)+=__________．19．(0分)[ID ：10014]函数21x y x +=-中，自变量x 的取值范围是 ． 20．(0分)[ID ：10013]如图，点E 在正方形ABCD 的边AB 上，若1EB，2EC =，那么正方形ABCD 的面积为_．21．(0分)[ID ：9980]如图，已知正方形ABCD ，以BC 为边作等边△BCE ，则∠DAE 的度数是_____．22．(0分)[ID ：9972]211a a a a--=，则a 的取值范围是________ 23．(0分)[ID ：9950]在平行四边形ABCD 中，若∠A+∠C=140°，则∠B= ．24．(0分)[ID ：9947]如图，矩形ABCD 中，15cm AB =，点E 在AD 上，且9cm AE =，连接EC ，将矩形ABCD 沿直线BE 翻折，点A 恰好落在EC 上的点A'处，则'A C =____________cm ．25．(0分)[ID：9940]如图，在∠MON的两边上分别截取OA、OB，使OA＝OB；分别以点A、B为圆心，OA长为半径作弧，两弧交于点C；连接AC、BC、AB、OC．若AB＝2cm，四边形OACB的面积为4cm2．则OC的长为_____cm．三、解答题26．(0分)[ID：10116]计算：（1）1 27123-+=（2）(3622)2-÷=27．(0分)[ID：10105]邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作;……依此类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形．如图1，平行四边形ABCD中，若AB=1，BC=2，则平行四边形ABCD为1阶准菱形．（1）判断与推理：①邻边长分别为2和3的平行四边形是_________阶准菱形；②为了剪去一个菱形，进行如下操作：如图2，把平行四边形ABCD沿BE折叠（点E在AD上），使点A落在BC边上的点F，得到四边形ABFE，请证明四边形ABFE是菱形；（2）操作与计算：已知平行四边形ABCD的邻边长分别为l，a（a>1），且是3阶准菱形，请画出平行四边形ABCD及裁剪线的示意图，并在图形下方写出a的值．28．(0分)[ID：10086]如图，方格纸中的每个小正方形的边长都是1，请在方格纸中画出1一个边长为22，且面积为6的等腰三角形（各顶点必须与方格纸中小正方形的顶点重合）．29．(0分)[ID：10054]在Rt△ABC中，∠BAC=90°,D是BC的中点，E是AD的中点．过点A作AF∥BC交BE的延长线于点F（1）求证：△AEF≌△DEB；（2）证明四边形ADCF是菱形；（3）若AC=4，AB=5，求菱形ADCFD 的面积．30．(0分)[ID：10046]一次函数y1＝kx+b和y2＝﹣4x+a的图象如图所示，且A（0，4），C（﹣2，0）．（1）由图可知，不等式kx+b＞0的解集是；（2）若不等式kx+b＞﹣4x+a的解集是x＞1．①求点B的坐标；②求a的值．【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．D2．D3．C4．A5．A6．D7．B8．D9．D10．A11．C12．B13．B14．C15．C二、填空题16．1【解析】【分析】根据平均数求得a的值然后根据众数求得b的值后再确定新数据的中位数【详解】试题分析：∵一组数据12a的平均数为2∴1+2+a=3×2解得a=3∴数据﹣la12b的唯一众数为﹣l∴b=17．＞【解析】【分析】根据实数大小比较的方法比较即可【详解】解：∵5=∴5故答案为＞【点睛】本题考查实数大小的比较熟练掌握实数大小的比较方法是解题关键18．3+2【解析】【分析】【详解】解：故答案为：3+219．x≠1【解析】x≠120．【解析】【分析】根据勾股定理求出BC根据正方形的面积公式计算即可【详解】解：由勾股定理得正方形的面积故答案为：【点睛】本题考查了勾股定理如果直角三角形的两条直角边长分别是ab斜边长为c那么a2+b221．15°【解析】【分析】由正方形的性质和等边三角形的性质可得∠DAB=∠ABC=90°AB=BC=BE∠EBC=60°可求∠BAE=75°即可得∠DAE的度数【详解】∵四边形ABCD是正方形∴∠DAB22．【解析】【分析】根据二次根式得非负性求解即可【详解】解：∵成立则有：并且即：∴故答案为：【点睛】本题考查的是二次根式的取值范围在二次根式里被开方数必须是非负数23．110°【解析】试题解析：∵平行四边形ABCD∴∠A+∠B=180°∠A=∠C∵∠A+∠C=140°∴∠A=∠C=70°∴∠B=110°考点：平行四边形的性质24．8【解析】【分析】设A′C=xcm先根据已知利用AAS证明△A′BC≌△DCE得出A′C=DE=xcm则BC=AD=（9+x）cmA′B=AB=15cm然后在Rt△A′BC中由勾股定理可得BC2=A25．【解析】【分析】根据作法判定出四边形OACB是菱形再根据菱形的面积等于对角线乘积的一半列式计算即可得解【详解】根据作图AC＝BC＝OA∵OA＝OB∴OA＝OB＝BC＝AC∴四边形OACB是菱形∵AB三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1．D解析：D【解析】【分析】由矩形的性质可知CD=AB= 3，BC=AD= 4，结合A点坐标即可求得C点坐标.【详解】∵四边形ABCD是长方形，∴CD=AB= 3，BC=AD= 4，∵点A（﹣32，﹣1），∴点C的坐标为（﹣32+3，﹣1+4），即点C的坐标为（32，3），故选D．【点睛】本题考查了矩形的性质和坐标的平移，根据平移的性质解决问题是解答此题的关键．2．D解析：D【解析】【分析】寻找小于26的最大平方数和大于26的最小平方数即可.【详解】解：小于26的最大平方数为25，大于26的最小平方数为3656，故选择D.【点睛】本题考查了二次根式的相关定义.3．C解析：C【解析】【分析】先求出每边的平方，得出AB2+AC2=BC2，AD2+CD2=AC2，BD2+AB2=AD2，根据勾股定理的逆定理得出直角三角形即可．【详解】理由是：连接AC、AB、AD、BC、CD、BD，设小正方形的边长为1，由勾股定理得：AB2=12+22=5,AC2=22+42=20,AD2=12+32=10,BC2=52=25,CD2=12+32=10,BD2=12+22=5，∴AB2+AC2=BC2,AD2+CD2=AC2,BD2+AB2=AD2，∴△ABC、△ADC、△ABD是直角三角形，共3个直角三角形，故选C.【点睛】本题考查了勾股定理的逆定理，解题的关键是掌握勾股定理.4．A解析：A【解析】【分析】当OP垂直于直线y＝kx＋b时，由垂线段最短可知：OP＜2，故此函数在y轴的左侧有最小值，且最小值小于2，从而得出答案．【详解】解：如图所示：过点O作OP垂直于直线y＝kx＋b，∵OP垂直于直线y＝kx＋b，∴OP＜2，且点P的横坐标＜0．故此当x＜0时，函数有最小值，且最小值＜2，根据选项可知A符合题意．故选：A．【点睛】本题主要考查的是动点问题的函数图象，由垂线段最短判定出：当x＜0时，函数有最小值，且最小值小于2是解题的关键．5．A解析：A【解析】【分析】作CD ⊥x 轴于D ，作AE ⊥x 轴于E ，由AAS 证明△AOE ≌△OCD ，得出AE=OD ，OE=CD ，由点A 的坐标是（-3，1），得出OE=3，AE=1，∴OD=1，CD=3，得出C （1，3）即可．【详解】解：如图所示：作CD ⊥x 轴于D ，作AE ⊥x 轴于E ，则∠AEO=∠ODC =90°，∴∠OAE+∠AOE=90°，∵四边形OABC 是正方形，∴OA=CO ，∠AOC=90°，∴∠AOE+∠COD=90°，∴∠OAE=∠COD ，在△AOE 和△OCD 中，AEO ODC OAE COD OA CO ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AOE ≌△OCD （AAS ），∴AE=OD ，OE=CD ，∵点A 的坐标是（-3，1），∴OE=3，AE=1，∴OD=1，CD=3，∴C （1，3），故选：A ．【点睛】本题考查了正方形的性质、全等三角形的判定与性质、坐标与图形性质；熟练掌握正方形的性质，证明三角形全等是解题的关键．6．D解析：D【解析】【分析】连接OB ，根据等腰三角形三线合一的性质可得BO ⊥EF ，再根据矩形的性质可得OA=OB ，根据等边对等角的性质可得∠BAC=∠ABO ，再根据三角形的内角和定理列式求出∠ABO=30°，即∠BAC=30°，根据直角三角形30°角所对的直角边等于斜边的一半求出AC ，再利用勾股定理列式计算即可求出AB ．【详解】解：如图，连接OB ，∵BE=BF ，OE=OF ，∴BO ⊥EF ，∴在Rt △BEO 中，∠BEF+∠ABO=90°，由直角三角形斜边上的中线等于斜边上的一半可知：OA=OB=OC ，∴∠BAC=∠ABO ，又∵∠BEF=2∠BAC ，即2∠BAC+∠BAC=90°，解得∠BAC=30°，∴∠FCA=30°，∴∠FBC=30°，∵FC=2，∴3∴3，∴22AC BC -22(43)(23)-6，故选D ．【点睛】本题考查了矩形的性质，全等三角形的判定与性质，等腰三角形三线合一的性质，直角三角形30°角所对的直角边等于斜边的一半，综合题，但难度不大，（2）作辅助线并求出∠BAC=30°是解题的关键．7．B解析：B【解析】【分析】根据“两点之间线段最短”可知：小鸟沿着两棵树的树梢进行直线飞行，所行的路程最短，运用勾股定理可将两点之间的距离求出．【详解】如图，设大树高为AB=9m ，小树高为CD=4m ，过C 点作CE ⊥AB 于E ，则EBDC 是矩形，连接AC ，∴EB=4m ，EC=12m ，AE=AB-EB=9-4=5m ，在Rt △AEC 222251213AE EC m ++==．故小鸟至少飞行13m ．故选：B.【点睛】本题考查正确运用勾股定理．善于观察题目的信息是解题以及学好数学的关键．8．D解析：D【解析】【分析】根据一次函数的性质对D 进行判断；根据一次函数图象上点的坐标特征对A 、B 进行判断；根据一次函数的几何变换对C 进行判断．【详解】A 、图象过点()0,1-，不符合题意；B 、函数的图象与x 轴的交点坐标是1(,0)2，不符合题意；C 、图象沿y 轴向上平移1个单位长度，得到直线2y x =，不符合题意；D 、图象经过第一、三、四象限，符合题意；故选：D ．【点睛】本题考查了一次函数的性质、一次函数图象上点的坐标特征和一次函数图象的几何变换，属于基础题． 9．D解析：D【解析】【分析】根据气温T 如何随时间t 的变化而变化图像直接可解答此题.【详解】A.根据图像4时气温最低，故A 错误；B.最低气温为零下3℃，故B 错误；C. 0点到14点之间气温先下降后上升，故C 错误；D 描述正确.【点睛】本题考查了学生看图像获取信息的能力，掌握看图像得到有用信息是解决此题的关键.10．A解析：A【解析】【分析】根据题意和函数图象中的数据可以判断各个小题中的结论是否正确，从而可以解答本题．【详解】由图可得，甲步行的速度为：240÷4=60米/分，故①正确，乙走完全程用的时间为：2400÷（16×60÷12）=30（分钟），故②错误，乙追上甲用的时间为：16﹣4=12（分钟），故③错误，乙到达终点时，甲离终点距离是：2400﹣（4+30）×60=360米，故④错误，故选A．【点睛】本题考查了函数图象，弄清题意，读懂图象，从中找到必要的信息是解题的关键. 11．C解析：C【解析】【分析】根据二次根式的性质、二次根式的加法法则、除法法则计算，判断即可．【详解】==A选项成立，不符合题意；==B选项成立，不符合题意；==，C选项不成立，符合题意；22==D选项成立，不符合题意；故选C．【点睛】本题考查的是二次根式的混合运算，掌握二次根式的性质、二次根式的混合运算法则是解题的关键．12．B解析：B【解析】【分析】根据二次根式的性质，结合算术平方根的概念对每个选项进行分析，然后做出选择．【详解】A．≠A错误；B．=，故B正确；=，故C错误；C．3D．2=,故D错误．故选：B．【点睛】本题主要考查了二次根式的性质和二次根式的化简，熟练掌握运算和性质是解题的关键．13．B解析：B【解析】二次根式要求被开方数为非负数，易得B为二次根式.故选B.14．C解析：C【解析】【分析】先根据直角三角形的性质求出AC的长，再根据勾股定理即可得出结论．【详解】⊥于D，解：∵ABC中，CD AB∴∠ADC=90°，则ADC为直角三角形，∵E是AC的中点，DE=5，∴AC=2DE=10，在Rt ADC中，AD=6，AC=10，∴8CD=，故选：C．【点睛】本题考查的是直角三角形斜边上的中线，熟知在直角三角形中，斜边上的中线等于斜边的一半是解答此题的关键．15．C解析：C【解析】【分析】把A（﹣4，0）分别代入一次函数y=﹣x+m和y=2x+n中，求得m和n的值，根据所得的两个解析式，求得点B和点C的坐标，以BC为底，点A到BC的垂线段为高，求出△ABC的面积即可．【详解】把点A（﹣4，0）代入一次函数y=﹣x+m得：4+m=0，解得：m=﹣4，即该函数的解析式为：y=﹣x﹣4，把点A（﹣4，0）代入一次函数y=2x+n得：﹣8+n=0，解得：n=8，即该函数的解析式为：y=2x+8，把x=0代入y=﹣x﹣4得：y=0﹣4=﹣4，即B（0，﹣4），把x=0代入y=2x+8得：y=0+8=8，即C（0，8），则边BC的长为8﹣（﹣4）=12，点A到BC的垂线段的长为4，S△ABC11242=⨯⨯=24．故选C．【点睛】本题考查了一次函数图象上点的坐标特征，正确掌握代入法求一次函数的解析式是解题的关键．二、填空题16．1【解析】【分析】根据平均数求得a的值然后根据众数求得b的值后再确定新数据的中位数【详解】试题分析：∵一组数据12a的平均数为2∴1+2+a=3×2解得a=3∴数据﹣la12b的唯一众数为﹣l∴b=解析：1【解析】【分析】根据平均数求得a的值，然后根据众数求得b的值后再确定新数据的中位数．【详解】试题分析：∵一组数据1，2，a的平均数为2，∴1+2+a=3×2解得a=3∴数据﹣l，a，1，2，b的唯一众数为﹣l，∴b=﹣1，∴数据﹣1，3，1，2，b的中位数为1．故答案为1．【点睛】本题考查了平均数、众数及中位数的定义，解题的关键是正确的利用其定义求得未知数的值．17．＞【解析】【分析】根据实数大小比较的方法比较即可【详解】解：∵5=∴5故答案为＞【点睛】本题考查实数大小的比较熟练掌握实数大小的比较方法是解题关键解析：＞【解析】【分析】根据实数大小比较的方法比较即可．解：∵∴故答案为＞．【点睛】本题考查实数大小的比较，熟练掌握实数大小的比较方法是解题关键18．3+2【解析】【分析】【详解】解：故答案为：3+2解析：【解析】【分析】【详解】解：222故答案为：．19．x≠1【解析】x≠1解析：x≠1【解析】x-≠，x≠11020．【解析】【分析】根据勾股定理求出BC根据正方形的面积公式计算即可【详解】解：由勾股定理得正方形的面积故答案为：【点睛】本题考查了勾股定理如果直角三角形的两条直角边长分别是ab斜边长为c那么a2+b2解析：3．【解析】【分析】根据勾股定理求出BC，根据正方形的面积公式计算即可．【详解】解：由勾股定理得，BC==∴正方形ABCD的面积23==，BC故答案为：3．【点睛】本题考查了勾股定理，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．21．15°【解析】【分析】由正方形的性质和等边三角形的性质可得∠DAB=∠ABC=90°AB=BC=BE∠EBC=60°可求∠BAE=75°即可得∠DAE的度数【详解】∵四边形ABCD是正方形∴∠DAB解析：15°【解析】由正方形的性质和等边三角形的性质可得，∠DAB=∠ABC=90°，AB=BC=BE ，∠EBC=60°，可求∠BAE=75°，即可得∠DAE 的度数．【详解】∵四边形ABCD 是正方形∴∠DAB ＝∠ABC ＝90°，AB ＝BC ，∵△BEC 是等边三角形∴BC ＝BE ，∠EBC ＝60°∴AB ＝BE ＝BC ，∠ABE ＝∠ABC ﹣∠EBC ＝30°∴∠BAE ＝75°∴∠DAE ＝∠BAD ﹣∠BAE ＝15°故答案为15°. 【点睛】本题考查了正方形的性质，等边三角形的性质，熟记各性质并准确识图是解题的关键．22．【解析】【分析】根据二次根式得非负性求解即可【详解】解：∵成立则有：并且即：∴故答案为：【点睛】本题考查的是二次根式的取值范围在二次根式里被开方数必须是非负数解析：01a <≤【解析】【分析】根据二次根式得非负性求解即可．【详解】=成立， 则有：10a ->，0a ≠ ， 10aa ，即：0a >，∴01a <≤，故答案为：01a <≤．【点睛】本题考查的是二次根式的取值范围，在二次根式里被开方数，必须是非负数．23．110°【解析】试题解析：∵平行四边形ABCD ∴∠A+∠B=180°∠A=∠C ∵∠A+∠C=140°∴∠A=∠C=70°∴∠B=110°考点：平行四边形的性质解析：110°【解析】试题解析：∵平行四边形ABCD ，∴∠A+∠B=180°，∠A=∠C ，∵∠A+∠C=140°，∴∠A=∠C=70°，∴∠B=110°．考点：平行四边形的性质．24．8【解析】【分析】设A′C=xcm 先根据已知利用AAS 证明△A′BC ≌△DCE 得出A′C=DE=xcm 则BC=AD=（9+x ）cmA′B=AB=15cm 然后在Rt △A′BC 中由勾股定理可得BC2=A解析：8【解析】【分析】设A ′C=xcm ，先根据已知利用AAS 证明△A ′BC ≌△DCE ，得出A ′C=DE= xcm ，则BC=AD=（9+x ）cm ，A ′B=AB=15cm ，然后在Rt △A ′BC 中，由勾股定理可得BC 2=A ′B 2+A ′C 2，即可得方程，解方程即可求得答案【详解】解：∵四边形ABCD 是矩形，∴AB=CD=15cm ，∠A=∠D=90°，AD ∥BC ，AD=BC ，∴∠DEC=∠A ′CB ，由折叠的性质，得：A ′B=AB=15cm ，∠BA ′E=∠A=90°，∴A ′B=CD ，∠BA ′C=∠D=90°，在△A ′BC 和△DCE 中，BA C D A CB DEC A B CD ∠=∠⎧⎪∠=∠=''⎨'⎪⎩∴△A ′BC ≌△DCE （AAS ），∴A ′C=DE ，设A ′C=xcm ，则BC=AD=DE+AE=x+9（cm ），在Rt △A ′BC 中，BC 2=A ′B 2+A ′C 2，即（x+9）2=x 2+152，解得：x=8，∴A ′C=8cm ．故答案为：8．【点睛】此题考查了矩形的性质、全等三角形的判定与性质、勾股定理以及折叠的性质．此题难度适中，注意掌握数形结合思想与方程思想的应用，注意掌握折叠前后图形的对应关系．25．【解析】【分析】根据作法判定出四边形OACB 是菱形再根据菱形的面积等于对角线乘积的一半列式计算即可得解【详解】根据作图AC ＝BC ＝OA∵OA＝OB∴OA＝OB ＝BC ＝AC∴四边形OACB 是菱形∵AB解析：【解析】【分析】根据作法判定出四边形OACB 是菱形，再根据菱形的面积等于对角线乘积的一半列式计算即可得解．【详解】根据作图，AC ＝BC ＝OA ，∵OA ＝OB ，∴OA ＝OB ＝BC ＝AC ，∴四边形OACB 是菱形，∵AB ＝2cm ，四边形OACB 的面积为4cm 2， ∴12AB •OC ＝12×2×OC ＝4， 解得OC ＝4cm ．故答案为：4．【点睛】 本题考查菱形的判定与性质，菱形的面积.解决本题的关键是能根据题目中作图的过程得出线段的等量关系.三、解答题26．（1）3；（2）2-． 【解析】【分析】（1）先化简二次根式，再计算二次根式的加减法即可；（2）利用二次根式除法的分配律进行计算即可．【详解】（1）原式==（2）原式=2=．【点睛】本题考查了二次根式的加减法、除法运算，熟记运算法则是解题关键．27．（1）①2；②证明见解析；（2）作图见解析，a 的值分别是：a 1=4，a 2=52，a 3=53，a4=43．【解析】【分析】（1）①根据邻边长分别为2和3的平行四边形经过两次操作，即可得出所剩四边形是菱形，即可得出答案；②根据平行四边形的性质得出AE∥BF，进而得出AE=BF，即可得出答案；（2）利用3阶准菱形的定义，即可得出答案；根据a=6b+r，b=5r，用r表示出各边长，进而利用图形得出▱ABCD是几阶准菱形．【详解】解：（1）①邻边长分别为2和3的平行四边形是2阶准菱形；故答案为：2；②如图2，由BE是四边形ABFE的对称轴，即知∠ABE=∠FBE，且AB=BF，EA=EF，又因为AE∥BF，所以∠AEB=∠FBE，从而有∠AEB=∠ABE，因此AB=AE，据此可知AB=AE=EF=BF，故四边形ABFE为菱形；（2）如图，必为a＞3，且a=4；如图，必为2<a<3，且a=2.5；如图，必为32<a<2，且a-1+1(1)12a-=，解得a=53；如图，必为1<a<32，且3（a-1）=1，解得a=43综上所述，a的值分别是：a1=4，a2=52，a3=53，a4=43．【点睛】本题考查图形的剪拼，平行四边形的性质，菱形的性质，作图---应用与作图设计．28．见解析【解析】【分析】利用三角形面积求法以及等腰三角形的性质画出即可．【详解】如图所示，即为所求：【点睛】此题主要考查了等腰三角形的性质以及作图，熟练掌握等腰三角形的性质是关键．29．（1）证明详见解析；（2）证明详见解析；（3）10．【解析】【分析】（1）利用平行线的性质及中点的定义，可利用AAS证得结论；（2）由（1）可得AF=BD，结合条件可求得AF=DC，则可证明四边形ADCF为平行四边形，再利用直角三角形的性质可证得AD=CD，可证得四边形ADCF为菱形；（3）连接DF，可证得四边形ABDF为平行四边形，则可求得DF的长，利用菱形的面积公式可求得答案．【详解】（1）证明：∵AF∥BC，∴∠AFE=∠DBE，∵E是AD的中点，在△AFE 和△DBE 中，AFE DBE FEA BED AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AFE ≌△DBE （AAS ）；（2）证明：由（1）知，△AFE ≌△DBE ，则AF =DB ．∵AD 为BC 边上的中线∴DB =DC ，∴AF =CD ．∵AF ∥BC ，∴四边形ADCF 是平行四边形，∵∠BAC =90°，D 是BC 的中点，E 是AD 的中点，∴AD =DC =12BC ， ∴四边形ADCF 是菱形；（3）连接DF ，∵AF ∥BD ，AF =BD ，∴四边形ABDF 是平行四边形， ∴DF =AB =5， ∵四边形ADCF 是菱形，∴S 菱形ADCF =12AC ▪DF =12×4×5=10． 【点睛】本题主要考查菱形的性质及判定，利用全等三角形的性质证得AF=CD 是解题的关键，注意菱形面积公式的应用． 30．（1）x ＞﹣2；（2）①（1，6）；②10．【解析】【分析】（1）求不等式kx +b ＞0的解集，找到x 轴上方的范围就可以了，比C 点横坐标大就行了 （2）①我们可以先根据B ，C 两点求出k 值，因为不等式kx +b ＞﹣4x +a 的解集是x ＞1 所以B 点横坐标为1，利用x=1代入y 1＝kx +b ，即求出B 点的坐标;②将B 点代入y 2＝﹣4x +a 中即可求出a 值.解：（1）∵A（0，4），C（﹣2，0）在一次函数y1＝kx+b上，∴不等式kx+b＞0的解集是x＞﹣2，故答案为：x＞﹣2；（2）①∵A（0，4），C（﹣2，0）在一次函数y1＝kx+b上，∴b=4-2k+b=0⎧⎨⎩，得b=4k=2⎧⎨⎩，∴一次函数y1＝2x+4，∵不等式kx+b＞﹣4x+a的解集是x＞1，∴点B的横坐标是x＝1，当x＝1时，y1＝2×1+4＝6，∴点B的坐标为（1，6）；②∵点B（1，6），∴6＝﹣4×1+a，得a＝10，即a的值是10．【点睛】本题主要考查学生对于一次函数图像性质的掌握程度。

天津市耀华嘉诚国际中学2019-2020学年八年级下学期线上学习阶段性评估检测语文试题（PDF版）天津市耀华嘉诚国际中学2019—2020学年度第二学期线上学习阶段性评估检测八年级语文试卷第Ⅰ卷（50分）一、选择题（每小题2分，共50分）1.下列加点字注音正确的一项是A. 凫．水（fú）枸杞．(jǐ) 连翘．（qiào）戛．然而止(jiá)B. 糜．子（mí）锵．然(qiāng) 山麓．（lù）恣．意妄为(zì)C. 狩．猎（shǒu）两栖．（qī）窈．窕（yǎo）如法炮．制(páo)D. 褶．皱（zhě）幽悄．（qiǎo）俶．尔（chù）追本溯．源（sù）2. 下列词语中书写有误的一项是A. 燎原雾霭人情世故B. 躁热元霄翠羽流苏C. 辐射晦暗富贵荣华D. 严峻褪色叹为观止3.依次填入下列句中空缺处的词语恰当的一项是①加快实施教育扶贫工程，让贫困家庭子女都能接受公平有质量的教育，贫困代际传递。

②在实现中华民族伟大复兴的新征程上，应对重大挑战、重大风险、解决重大矛盾，迫切需要迎难而上、挺身而出的担当精神。

③当的现代社会与传统文化有了一次次美丽的“邂逅”，中华文化基因逐渐苏醒，这危机中的微熹，弥足珍贵。

A．阻挠抵制喧嚷 B．阻挠抵御喧嚣C．阻断抵御喧嚣 D．阻断抵制喧嚷4.下列语句中没有语病的一项是A.《舌尖上的中国》这部风靡海内外的纪录片，用镜头展示烹饪技术，用美味包裹乡愁，给观众带来了心灵的震撼。

B.川航机组突遇险情，成功备降，强烈地震撼着网友的心，纷纷为他们的专业素养点赞。

C.为了提高优秀传统文化特色，学校举办了“寻找家乡名人名画”的活动。

D.性格懦弱的李娟的母亲，面对突如其来的家庭变故，表现出了异常的坚韧。

5.下列句子中的标点符号使用有误的一项是A.姑苏城与金鸡湖，是苏州的双面绣：一面是古老的斑斓，一面是现代的辉煌！B.第四届世界互联网大会12月3日至5日举行，主题为《发展数字经济促进开放共享——携手共建网络空间命运共同体》。

一、选择题1．如图，OM 、ON 、OP 分别是AOB ∠，BOC ∠，AOC ∠的角平分线，则下列选项成立的（ ）A ．AOP MON ∠>∠B ．AOP MON ∠=∠C ．AOP MON ∠<∠D ．以上情况都有可能2．如图O 是ABC 内的一点，且O 到三边AB 、BC 、CA 的距离==OF OD OE ．若70A ∠=︒，则BOC ∠（ ）．A ．125°B ．135°C ．105°D ．100° 3．如图，,,AB AD CB CD AC BD ==、相交于点O ，则下列说法中正确的个数是（ ） ①OD OB =；②点O 到CB CD 、的距离相等；③BDA BDC ∠=∠；④BD AC ⊥A ．4B ．3C ．2D ．14．MAB ∠为锐角，AB a ，点C 在射线AM 上，点B 到射线AM 的距离为d ，BC x =，若△ABC 的形状、大小是唯一确定的，则x 的取值范围是（ ）A ．x d =或x a ≥B ．x a ≥C ．x d =D ．x d =或x a > 5．如图，已知ABC DCB ∠=∠，添加一个条件使ABC DCB △△≌，下列添加的条件不能使ABC DCB △△≌的是（ ）A ．A D ∠=∠B ．AB DC = C ．AC DB =D ．ACB DBC ∠=∠ 6．工人师傅常用直角尺平分一个角，做法如下：如图所示，在∠AOB 的边OA ，OB 上分别取OM ＝ON ，移动直角尺，使直角尺两边相同的刻度分别与M ，N 重合（即CM ＝CN ）．此时过直角尺顶点C 的射线OC 即是∠AOB 的平分线．这种做法的道理是（ ）A ．HLB ．SASC ．SSSD ．ASA7．如图所示，下面甲、乙、丙三个三角形和ABC 全等的图形是（ ）A ．甲和乙B ．乙和丙C ．只有丙D ．只有乙 8．下列各命题中，假命题是（ ）A ．有两边及其中一边上的中线对应相等的两个三角形全等B ．有两边及第三边上高对应相等的两个三角形全等C ．有两角及其中一角的平分线对应相等的两三角形全等D ．有两边及第三边上的中线对应相等的两三角形全等9．下列命题中，假命题是（ ）A ．在同一平面内，垂直于同一条直线的两直线平行B ．到线段两端点距离相等的点在这条线段的垂直平分线上C ．一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等D ．一边长相等的两个等腰直角三角形全等10．如图，已知△ABC 的周长是20，OB ，OC 分别平分∠ABC 和∠ACB ，OD ⊥BC 于，且OD=2，△ABC 的面积是（ ）A ．20B ．24C ．32D ．4011．如图所示，已知∠A ＝∠C ，∠AFD ＝∠CEB ，那么给出的条件不能得到ADF CBE △≌△是（ ）A ．∠B ＝∠D B ．EB=DFC ．AD=BCD ．AE=CF 12．如图，AC 与DB 相交于E ，且BE CE =，如果添加一个条件还不能判定ABE △≌DCE ，则添加的这个条件是（ ）．A ．AC DB = B ．A D ∠=∠C ．B C ∠=∠D ．AB DC = 13．如图，AB ＝AC ，点D 、E 分别是AB 、AC 上一点，AD ＝AE ，BE 、CD 相交于点M ．若∠BAC ＝70°，∠C ＝30°，则∠BMD 的大小为( )A ．50°B ．65°C ．70°D ．80°14．如图，在△ABC 中，点E 和F 分别是AC ，BC 上一点，EF ∥AB ，∠BCA 的平分线交AB 于点D ，∠MAC 是△ABC 的外角，若∠MAC ＝α，∠EFC ＝β，∠ADC ＝γ，则α、β、γ三者间的数量关系是（ ）A ．β＝α+γB ．β＝2γ﹣αC ．β＝α+2γD ．β＝2α﹣2γ 15．下列命题，真命题是（ ）A ．全等三角形的面积相等B ．面积相等的两个三角形全等C ．两个角对应相等的两个三角形全等D ．两边和其中一边的对角对应相等的两个三角形全等二、填空题16．如图，已知在ABC ∆和ADC ∆中，,ACB ACD ∠=∠请你添加一个条件：_________，使ABC ADC ∆≅∆(只添一个即可）．17．如图，点D 、E 分别在线段AB 、AC 上，BE 与CD 相交于点O ．若AB AC =，AD AE =，60A ∠=︒，80ADC ∠=︒，则B 的度数为______．18．如图，两根旗杆间相距22米，某人从点B 沿BA 走向点A ，一段时间后他到达点M ，此时他分别仰望旗杆的顶点C 和D ，两次视线的夹角为90°，且CM DM =．已知旗杆BD 的高为12米，该人的运动速度为2米/秒，则这个人运动到点M 所用时间是________秒．19．如图，在△ABC 中，∠C ＝90°，AD 是∠BAC 的角平分线，若BC ＝8cm ，BD ＝5cm ，AB=10cm,则S △ABD =______．20．如图，∠1＝∠2，要使△ABC ≌△ADC ，还需添加条件：_____．（填写一个你认为正确的即可）21．如图，在Rt ABC 中，90C ∠=︒，AD AC =，DE AB ⊥，交BC 于点E ．若26B ∠=︒，则AEC ∠=______︒．22．如图，△ACB 和△DCE 中，AC ＝BC ，∠ACB ＝∠DCE ＝90°，∠ADC ＝∠BEC ，若AB ＝17，BD ＝5，则S △BDE ＝_______．23．如图，已知△ABC 的面积为18，BP 平分∠ABC ，且AP ⊥BP 于点P ，则△BPC 的面积是_____．24．如图，AD 是ABC 中BAC ∠的平分线，DE AB ⊥交AB 于点E ，DF AC ⊥交AC 于点F ．若28ABC S =，4DE =，8AB =，则AC =_________．25．如图，已知ABC DCB ∠=∠，则需添加的一个条件是______可使ACB DBC ≌．（只写一个即可，不添加辅助线）．26．如图，在△ABC 中，∠C =90°，∠A 的平分线交BC 于D ，若20ABD S ∆=cm 2，AB =10cm ，则CD 为__________cm ．三、解答题27．如图，点P 是锐角∠ABC 内一点，BP 平分∠ABC ，点M 在边BA 上，点N 在边BC 上，且PM ＝PN ．求证：∠BMP ＋∠BNP ＝180°．28．如图，在△ABD中，∠ABC=45°，AC，BF为△ABD的两条高，CM//AB，交AD于点M；求证：BE=AM+EM．29．按要求作图a b（不要求写作法，只保留（1）如图，已知线段,a b，用尺规做一条线段，使它等于作图痕迹）（2）已知：∠α，求作∠AOB=∠α（要求：直尺和圆规作图，不写作法，保留作图痕迹）30．如图，点B，F，C，E在一条直线上，FB=CE，AB∥ED，AC∥FD．求证：AB=DE．。

天津耀华嘉诚国际中学八年级下册期末物理试卷含答案一、选择题1．下列数据最符合生活实际的是（）A．八年级下册物理教材的厚度约为10cmB．一个中学生的质量约为50kgC．一个鸡蛋重约为5ND．一个中学生的重力约为50N2．如图所示为一种常用核桃夹，用大小相同的力垂直作用在B点比A点更易夹碎核桃，这说明为的作用效果与（）A．力的作用点有关B．力的方向有关C．力的大小有关D．受力面积有关3．如图所示是“探究阻力对物体运动的影响”的实验，下列有关叙述正确的是（）A．三次实验小车从斜面静止下滑的位置可以不同B．运动的小车最终会停下来，说明物体的运动需要力来维持C．实验表明，小车受到的阻力越小，运动的距离越远D．根据二次实验现象进一步推理可以得出牛顿第一定律4．生活中处处有物理，下列与压强知识有关的说法中，正确的是（）A．书包背带做得宽而平，是为了增加受力面积从而增大压强B．能用吸管将杯中饮料吸进嘴里，是利用了大气压强C．大气压强是随着海拔的升高而增大D．在气体和液体中，流速越大的位置，压强越大5．下列应用到流体压强与流速关系的是（）A．墙壁上的吸盘B．升空的孔明灯C．三峡船闸D．客机起飞6．如图所示，在水平力F的作用下，使硬棒沿逆时针方向匀速转动，在棒与竖直方向的夹角由θ增大到θ′的过程中（）A．拉力F变小，F的力臂变小B．拉力F变大，F的力臂变大C．重力G不变，G的力臂变大D．重力G不变，G的力臂变小7．如图所示，甲、乙两杯液体静止放在水平桌面上，把同一个鸡蛋分别放入甲、乙两杯液体中，鸡蛋在甲杯中漂浮，在乙杯中悬浮，此时两液面相平。

下列说法中正确的是（）A．两杯液体对容器底部的压强相等B．两杯液体的密度相等C．鸡蛋在甲、乙两杯液体中受到的浮力相等D．在甲杯液体中加入食盐溶化后，鸡蛋会下沉一些8．下图为起重机的钢丝绳吊着6×105N的重物匀速上升的图象，能正确反映钢丝绳的拉力所做的功与时间关系的是（）A．B．C． D．二、填空题9．网球运动员挥拍击球时，球拍的网面凹陷，说明力可以改变物体的 ______；网球在离开网面时，球网的 ______转化为网球的动能。