初中物理受力分析专题 .ppt
- 格式:ppt
- 大小:1.48 MB
- 文档页数:88



受力分析专题一、受力分析1、定义:把某个特定的物体在某个特定的物理环境中所受到的力一个不漏,一个不重地找出来,并画出定性的受力示意图。
对物体进行正确地受力分析,是解决好力学问题的关键。
2、为了在受力分析时不多分析力,也不漏力,一般情况下按下面的步骤进行:(1)确定研究对象 —可以是某个物体也可以是整体。
(2)按顺序画力①.先画重力:作用点画在物体的重心,方向竖直向下。
②.次画已知力③.再画接触力—(弹力和摩擦力):看研究对象跟周围其他物体有几个接触点(面),先对某个接触点(面)分析,若有挤压,则画出弹力,若还有相对运动或相对运动的趋势,则再画出摩擦力。
分析完一个接触点(面)后,再依次分析其他的接触点(面)。
④.再画其他场力:看是否有电、磁场力作用,如有则画出。
二、受力分析的方法1、整体法:以几个物体构成的整个系统为研究对象进行求解的方法。
2、隔离法:把系统分成若干部分并隔离开来,分别以每一部分为研究对象进行受力分析,分别列出方程,再联立求解的方法。
3、通常在分析外力对系统作用时,用整体法;在分析系统内各物体之间的相互作用时,用隔离法。
有时在解答一个问题时要多次选取研究对象,需要整体法与隔离法交叉使用。
三、受力分析的判断依据:①从力的概念判断,寻找施力物体;②从力的性质判断,寻找产生原因;③从力的效果判断,寻找是否产生形变或改变运动状态。
总之,在进行受力分析时一定要按次序画出物体实际受的各个力,为解决这一难点可记忆以下受力口诀:地球周围受重力 绕物一周找弹力考虑有无摩擦力 其他外力细分析合力分力不重复 只画受力抛施力四、例题例1、单个物体受力情况例2、两个物体受力情况【例题】1、一个放在水平桌面上的物体,受到分别为5牛和3牛的两个力F1、F 2的作用后仍处于静止状态,如图8所示,则该物体受到的合力为 ,桌面对此物体的摩擦力大小为 ,方向为 。
2、一物体做匀速直线运动,在所受的多个力中,有一对大小为15N 的平衡力,当这对力突然消失后,该物体的运动状态将_______________(填“改变”或“不变”).3、一个小球重3牛顿,当它以0.5米/秒的速度在光滑的平面上作匀速直线运动时,加在小球上的水平推力是( )A、0牛顿B、1.5牛顿C、3牛顿D、无法判断。

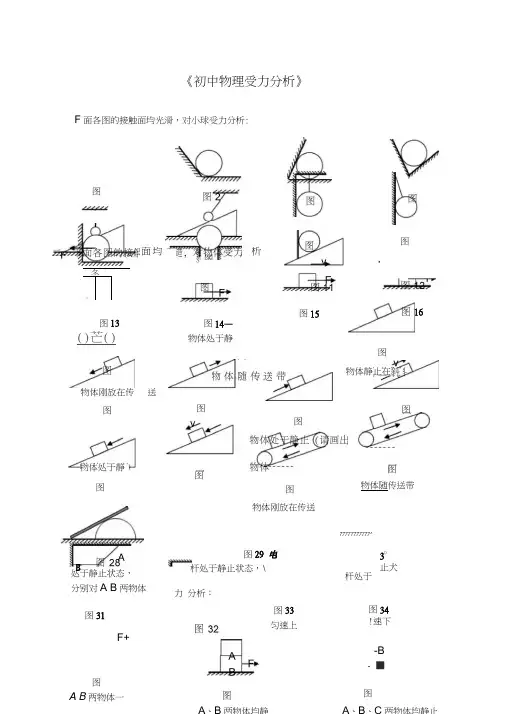
《初中物理受力分析》F面各图的接触面均光滑,对小球受力分析:图面虫析均冬广才丿S3-图15图16图13()芒()图14—物体处于静图物体刚放在传图物体静止在斜图送图图物体处于静图图图图物体随传送带B处于静止状态,分别对A B两物体物体刚放在传送77777777777^图29 电杆处于静止状态,\力分析:图31F+图A B两物体一杆处于30止犬图33匀速上图34!速下-B- ■图(9A 、B 两物体一起匀速(对物体A 进行受力分析⑹引⑷⑺z(12以下各球均为光滑刚性(15滑轮重力(18(19(20(21(22(23(24 OB表面光另分J5A B匀速运动 A B匀速运动芒(36(34(35ABC三者的受力图(39A沿墙壁向上匀速滑动此环为轻环,重力忽略(43(44(45AA匀速上升上升,保持在原来的高度。
(46 初三数4学圆教案(48一、本章知识框架二、本章重点:纟1 •圆的定义:纟⑴线段0A绕着它的一个端点O旋转一周,⑵圆是到定点的距离等于定长的点的集合.2 •判定一个点P是否在。
O上.d>r :-点P在。
O夕卜;d = r :-点P在。
O 上;dvr :-点P在。
O内.3. 与圆有关的角(1) 圆心角:顶点在圆心的角叫圆心角.圆心角的性质:圆心角的度数等于它所对的弧的度数.⑵圆周角:顶点在圆上,两边都和圆相交的角叫做圆周角.圆周角的性质:①圆周角等于它所对的弧所对的圆心角的一半.②同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.③90。
的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.④如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.⑤圆内接四边形的对角互补;外角等于它的内对角.⑶弦切角:顶点在圆上虽往上和圆相交,另一边和圆相切的角叫弦切角. 弦切角的性质:弦切角等于它夹的弧所对的圆周角.弦切角的度数等于它夹的弧的度数的一半.4. 圆的性质:⑴旋转不变性:圆是旋升对保图形,绕圆心旋转任一角度都和原来图形重合;圆是中心对称图形,对称中心是圆心.'在同圆或等圆中,两个圆心角,两条弧,两条弦,两条弦心距,这四组量中的任意一组相等,那么它所对应的其他各组分别相等.⑵轴对称:圆是轴对称图形,经过圆心的任一直线都是它的对称轴. 垂径定理及推论:(1) 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.(2) 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.(3) 弦的垂直平分线过圆心,且平分弦对的两条弧.(4) 平分一条弦所对的两条弧的直线过圆心,且垂直平分此弦.(5) 平行弦夹的弧相等.5 •三角形的内心、外心、重心、垂心(1) 三角形的内心:是三角形三个角平分线的交点,它是三角形内切圆的圆心,在三角形内部,它到三角形三边的距离相等,通常用“ I”表示.(2) 三角形的外心:是三角形三边中垂线的交点,它是三角形外接圆的圆心,锐角三角形外心在三角形内部,直角三角形的外心是斜边中点,钝角三角形外心在三角形外部,三角形外心到三角形三个顶点的距离相等,通常用0表示.⑶三角形重心:是三角形三边中线的交点,在三角形内部;它到顶点的距离是到对边中点距离的2倍,通常用G表示.(4)垂心:是三角形三边高线的交点.6. 切线的判定、性质:(1)切线的判定:①经过半径的外端并且垂直于这条半径的直线是圆的切线.②到圆心的距离d等于圆的半径的直线是圆的切线.⑵切线的性质:①圆的切线垂直于过切点的半径.②经过圆心作圆的切线的垂线经过切点.③经过切点作切线的垂线经过圆心.⑶切线长:从圆外一点作圆的切线,这一点和切点之间的线段的长度叫做切线长.⑷切线长定理:从圆外一点作圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.7. 圆内接四边形和外切四边形(1)四个点都在圆上的四边形叫圆的内接四边形,圆内接四边形对角互补,外角等于内对角.⑵各边都和圆相切的四边形叫圆外切四边形,圆外切四边形对边之和相等.8. 直线和圆的位置关系:设。