重庆市巴蜀中学2015-2016学年高一数学下学期期末考试试题文(扫描版)
- 格式:doc
- 大小:7.00 MB
- 文档页数:7


2015-2016学年重庆一中高一(下)期末数学试卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={x|(x+2)(x﹣3)<0},B={﹣1,0,1,2,3},则A∩B=()A.{0,1}B.{0,1,2}C.{﹣1,0,1}D.{﹣1,0,1,2} 2.(5分)设=(k+2,k),=(3,1),若⊥,则实数k的值等于()A.﹣B.﹣C.D.3.(5分)设等差数列{a n}的前n项和为S n,若a5+a14=10,则S18等于()A.20B.60C.90D.1004.(5分)圆(x+2)2+y2=4与圆(x﹣2)2+(y﹣1)2=9的位置关系为()A.内切B.相交C.外切D.相离5.(5分)已知变量x,y满足约束条件,则z=3x+y的最大值为()A.12B.11C.3D.﹣16.(5分)等比数列{a n}中,a1=1,q=2,则T n=++…+的结果可化为()A.1﹣B.1﹣C.(1﹣)D.(1﹣)7.(5分)“m=1”是“直线mx+y﹣2=0与直线x+my+1﹣m=0平行”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8.(5分)阅读如图的程序框图,运行相应的程序,输出S的值为()A.15B.105C.245D.9459.(5分)现有两组卡片,第一组卡片上分别写有数字“2,3,4”,第二组卡片上分别写有数字“3,4,5”,现从每组卡片中各随机抽出一张,用抽取的第一组卡片上的数字减去抽取的第二组卡片上的数字,差为负数的概率为()A.B.C.D.10.(5分)在平行四边形ABCD中,AD=2,∠BAD=60°,E为CD的中点,若•=1,则AB的长为()A.B.4C.5D.611.(5分)已知函数f(x)=,且对于任意实数a∈(0,1)关于x的方程f(x)﹣a=0都有四个不相等的实根x1,x2,x3,x4,则x1+x2+x3+x4的取值范围是()A.(2,4]B.(﹣∞,0]∪[4,+∞)C.[4,+∞)D.(2,+∞)12.(5分)已知集合M={(x,y)|2x+y﹣4=0},N={(x,y)|x2+y2+2mx+2ny=0},若M ∩N≠∅,则m2+n2的最小值()A.B.C.(6﹣2)D.二、填空题:本大题共4小题,每小题5分13.(5分)某学校高一、高二、高三年级的学生人数之比为3:3:4,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高一年级抽取.14.(5分)在△ABC中,角A,B,C所对边长分别为a,b,c,若a=3,B=,cos A=,则b=.15.(5分)已知点P,Q为圆C:x2+y2=25上的任意两点,且|PQ|<6,若PQ中点组成的区域为M,在圆C内任取一点,则该点落在区域M上的概率为.16.(5分)点C是线段AB上任意一点,O是直线AB外一点,,不等式x2(y+1)+y2(x+2)>k(x+2)(y+1)对满足条件的x,y恒成立,则实数k的取值范围.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(10分)已知△ABC的面积是3,角A,B.C所对边长分别为a,b,c,cos A=.(Ⅰ)求;(Ⅱ)若b=2,求a的值.18.(12分)已知圆C:(x﹣3)2+(y﹣4)2=4,直线l过定点A(1,0).(1)若l与圆C相切,求l的方程;(2)若l与圆C相交于P、Q两点,若|PQ|=2,求此时直线l的方程.19.(12分)某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图.(1)求图中实数a的值;(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的人数;(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.20.(12分)已知数列{a n}满足a1=1,a n﹣a n﹣1=n(其中n≥2且n∈N).(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=,其前n项和是T n,求证:T n<.21.(12分)已知动点P(x,y)满足方程xy=1(x>0).(Ⅰ)求动点P到直线l:x+2y﹣=0距离的最小值;(Ⅱ)设定点A(a,a),若点P,A之间的最短距离为2,求满足条件的实数a的取值.22.(12分)已知函数f(x)=为奇函数,且f(1)=1.(Ⅰ)求实数a与b的值;(Ⅱ)若函数g(x)=,设{a n}为正项数列,且当n≥2时,[g(a n)•g(a n﹣1)+]•a n2=q,(其中q≥2016),{a n}的前n项和为S n,b n=,若b n≥2017n恒成立,求q的最小值.2015-2016学年重庆一中高一(下)期末数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={x|(x+2)(x﹣3)<0},B={﹣1,0,1,2,3},则A∩B=()A.{0,1}B.{0,1,2}C.{﹣1,0,1}D.{﹣1,0,1,2}【解答】解:集合A={x|(x+2)(x﹣3)<0}=(﹣2,3),B={﹣1,0,1,2,3},则A∩B={﹣1,0,1,2},故选:D.2.(5分)设=(k+2,k),=(3,1),若⊥,则实数k的值等于()A.﹣B.﹣C.D.【解答】解:∵设=(k+2,k),=(3,1),⊥,∴•=3(k+2)+k=0,解得k=﹣,故选:A.3.(5分)设等差数列{a n}的前n项和为S n,若a5+a14=10,则S18等于()A.20B.60C.90D.100【解答】解:∵等差数列{a n}的前n项和为S n,a5+a14=10,∴S18=(a1+a18)=(a5+a14)=9×10=90.故选:C.4.(5分)圆(x+2)2+y2=4与圆(x﹣2)2+(y﹣1)2=9的位置关系为()A.内切B.相交C.外切D.相离【解答】解:圆(x+2)2+y2=4的圆心C1(﹣2,0),半径r=2.圆(x﹣2)2+(y﹣1)2=9的圆心C2(2,1),半径R=3,两圆的圆心距d==,R+r=5,R﹣r=1,R+r>d>R﹣r,所以两圆相交,故选:B.5.(5分)已知变量x,y满足约束条件,则z=3x+y的最大值为()A.12B.11C.3D.﹣1【解答】解:画出可行域如图阴影部分,由得C(3,2)目标函数z=3x+y可看做斜率为﹣3的动直线,其纵截距越大,z越大,由图数形结合可得当动直线过点C时,z最大=3×3+2=11故选:B.6.(5分)等比数列{a n}中,a1=1,q=2,则T n=++…+的结果可化为()A.1﹣B.1﹣C.(1﹣)D.(1﹣)【解答】解:等比数列{a n}中,∵a1=1,q=2,∴a n a n+1=22n﹣1,∴T n=++…+===.故选:C.7.(5分)“m=1”是“直线mx+y﹣2=0与直线x+my+1﹣m=0平行”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解答】解:m=1时,直线mx+y﹣2=0与直线x+my+1﹣m=0相互平行,是充分条件,若直线mx+y+2=0与直线x+my+1﹣m=0相互平行,则,解得:m=1,是必要条件,故选:C.8.(5分)阅读如图的程序框图,运行相应的程序,输出S的值为()A.15B.105C.245D.945【解答】解:由程序框图知:算法的功能是求S=1×3×5×…×(2i+1)的值,∵跳出循环的i值为4,∴输出S=1×3×5×7=105.故选:B.9.(5分)现有两组卡片,第一组卡片上分别写有数字“2,3,4”,第二组卡片上分别写有数字“3,4,5”,现从每组卡片中各随机抽出一张,用抽取的第一组卡片上的数字减去抽取的第二组卡片上的数字,差为负数的概率为()A.B.C.D.【解答】解:列表得:所有等可能的情况有9种,其中差为负数的情况有6种,则P==.故选:D.10.(5分)在平行四边形ABCD中,AD=2,∠BAD=60°,E为CD的中点,若•=1,则AB的长为()A.B.4C.5D.6【解答】解:如图所示,由题意可得,•=•(+)=•+•=2﹣,=22﹣cos60°=1,||=6,即AB的长为6,故选:D.11.(5分)已知函数f(x)=,且对于任意实数a∈(0,1)关于x的方程f(x)﹣a=0都有四个不相等的实根x1,x2,x3,x4,则x1+x2+x3+x4的取值范围是()A.(2,4]B.(﹣∞,0]∪[4,+∞)C.[4,+∞)D.(2,+∞)【解答】解:函数f(x)=,可知x≤1时,函数是圆的上半部分,函数的最大值为1,x>1时,f(x)=﹣x2+2mx﹣2m+1,的对称轴为x=m,开口向下,对于任意实数a∈(0,1)关于x的方程f(x)﹣a=0都有四个不相等的实根x1,x2,x3,x4,则x>1时,函数的最大值中的最小值为1,此时m≥2,在平面直角坐标系中,画出函数y=f(x)与y=a的图象如图:x1+x2=0,x3+x4≥2m≥4,则x1+x2+x3+x4的取值范围是[4,+∞).故选:C.12.(5分)已知集合M={(x,y)|2x+y﹣4=0},N={(x,y)|x2+y2+2mx+2ny=0},若M ∩N≠∅,则m2+n2的最小值()A.B.C.(6﹣2)D.【解答】解:由题意,可知集合M={(x,y)|2x+y﹣4=0},N={(x,y)|x2+y2+2mx+2ny =0},且M∩N≠∅,∴表示直线2x+y﹣4=0与圆x2+y2+2mx+2ny=0有交点,即圆心(﹣m,﹣n)到直线2x+y ﹣4=0的距离不大于半径,∴d=≤,设m2+n2=r2,m=r cosα,n=r sinα,∴﹣r≤2r cosα+r sinα+4≤r,∴r≥∴r≥,∴r2≥,∴m2+n2的最小值为.故选:A.二、填空题:本大题共4小题,每小题5分13.(5分)某学校高一、高二、高三年级的学生人数之比为3:3:4,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高一年级抽取15.【解答】解:∵高一、高二、高三年级的学生人数之比为3:3:4,∴高一在总体中所占的比例是,∵用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,∴要从高一抽取×50=15,故答案为:15.14.(5分)在△ABC中,角A,B,C所对边长分别为a,b,c,若a=3,B=,cos A=,则b=2.【解答】解:∵a=3,B=,cos A=,∴sin A==,∴由正弦定理可得:b===2.故答案为:2.15.(5分)已知点P,Q为圆C:x2+y2=25上的任意两点,且|PQ|<6,若PQ中点组成的区域为M,在圆C内任取一点,则该点落在区域M上的概率为.【解答】解:当|PQ|=6时,圆心到线段PQ的距离d==4.此时M位于半径是4的圆上,∴|PQ|<6,∴PQ中点组成的区域为M为半径为4的圆与半径为5的圆组成的圆环,即16<x2+y2<25,PQ中点组成的区域为M如图所示,那么在C内部任取一点落在M内的概率为=,故答案为:.16.(5分)点C是线段AB上任意一点,O是直线AB外一点,,不等式x2(y+1)+y2(x+2)>k(x+2)(y+1)对满足条件的x,y恒成立,则实数k的取值范围.【解答】解:点C是线段AB上任意一点,O是直线AB外一点,∴x+y=1,x,y∈[0,1],将y=1﹣x代入不等式x2(y+1)+y2(x+2)>k(x+2)(y+1)中,可得2x2﹣3x+2>k(4﹣x2),即k<,令f(x)=,x∈[0,1],对f(x)求导,得f′(x)=,令f′(x)>0,解得:<x<1,f′(x)<0,解得:0<x<,∴f(x)在[0,]上递减,在[,1]上递增,当x=时,f(x)有最小值,最小值为,所以当k<时,不等式恒成立,故答案为:.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(10分)已知△ABC的面积是3,角A,B.C所对边长分别为a,b,c,cos A=.(Ⅰ)求;(Ⅱ)若b=2,求a的值.【解答】解:(Ⅰ)在△ABC中,由,得.又bc sin A=3,,∴bc=10.∴.(Ⅱ)∵b=2,可得:c=5,∴由余弦定理可得:a2=b2+c2﹣2bc cos A=13,∴解得:.18.(12分)已知圆C:(x﹣3)2+(y﹣4)2=4,直线l过定点A(1,0).(1)若l与圆C相切,求l的方程;(2)若l与圆C相交于P、Q两点,若|PQ|=2,求此时直线l的方程.【解答】解:(1)若直线l的斜率不存在,则直线l:x=1,符合题意.若直线l斜率存在,设直线l的方程为y=k(x﹣1),即kx﹣y﹣k=0.由题意知,圆心(3,4)到已知直线l的距离等于半径2,即:=2,解之得k=,此时直线的方程为3x﹣4y﹣3=0.综上可得,所求直线l的方程是x=1或3x﹣4y﹣3=0.(2)直线与圆相交,斜率必定存在,且不为0,设直线方程为kx﹣y﹣k=0,因为|PQ|=2=2=2,求得弦心距d=,即=,求得k=1或k=7,所求直线l方程为x﹣y﹣1=0或7x﹣y﹣7=0.19.(12分)某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图.(1)求图中实数a的值;(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的人数;(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.【解答】(1)解:由于图中所有小矩形的面积之和等于1,∴10×(0.005+0.01+0.02+a+0.025+0.01)=1.解得a=0.03.(2)解:根据频率分布直方图,成绩不低于6(0分)的频率为1﹣10×(0.005+0.01)=0.85.由于该校高一年级共有学生640人,利用样本估计总体的思想,可估计该校高一年级数学成绩不低于6(0分)的人数约为640×0.85=544人.(3)解:成绩在[40,50)分数段内的人数为40×0.05=2人,分别记为A,B.成绩在[90,100]分数段内的人数为40×0.1=4人,分别记为C,D,E,F.(7分)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,则所有的基本事件有:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种.(9分)如果两名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,那么这两名学生的数学成绩之差的绝对值一定不大于10.如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内,那么这两名学生的数学成绩之差的绝对值一定大于10.记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,则事件M包含的基本事件有:(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共7种.所以所求概率为P(M)=.20.(12分)已知数列{a n}满足a1=1,a n﹣a n﹣1=n(其中n≥2且n∈N).(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=,其前n项和是T n,求证:T n<.【解答】(Ⅰ)解:a n=a1+(a2﹣a1)+(a3﹣a2)+…+(a n﹣a n﹣1)=.(Ⅱ)证明:,其前n项和T n=++…+,T n=++…++,∴T n=+++…+﹣,=+﹣=﹣,∴T n=﹣<.21.(12分)已知动点P(x,y)满足方程xy=1(x>0).(Ⅰ)求动点P到直线l:x+2y﹣=0距离的最小值;(Ⅱ)设定点A(a,a),若点P,A之间的最短距离为2,求满足条件的实数a的取值.【解答】解:(Ⅰ)由点到直线的距离公式可得:,当且仅当时距离取得最小值.(Ⅱ)设点(x>0),则,设(t≥2),则,,设f(t)=(t﹣a)2+a2﹣2(t≥2)对称轴为t=a分两种情况:(1)a≤2时,f(t)在区间[2,+∞)上是单调增函数,故t=2时,f(t)取最小值∴,∴a2﹣2a﹣3=0,∴a=﹣1(a=3舍).(2)a>2时,∵f(t)在区间[2,a]上是单调减,在区间[a,+∞)上是单调增,∴t=a时,f(t)取最小值,∴,∴((舍),综上所述,a=﹣1或.22.(12分)已知函数f(x)=为奇函数,且f(1)=1.(Ⅰ)求实数a与b的值;(Ⅱ)若函数g(x)=,设{a n}为正项数列,且当n≥2时,[g(a n)•g(a n﹣1)+]•a n2=q,(其中q≥2016),{a n}的前n项和为S n,b n=,若b n≥2017n恒成立,求q的最小值.【解答】解:(Ⅰ)因为f(x)为奇函数,,得b=0,又f(1)=1,得a=1;(Ⅱ)由,得,且,∴∴,∴.由:(q≥2016),∵b n≥2017n恒成立,即:≥2017n恒成立,当q≥2016时,∵,再由复合函数单调性知,数列为单调递减数列,且n→∞时,,当q≥2017时,中的每一项都大于2017,∴≥2017n恒成立;当q∈[2016,2017)时,数列为单调递减数列,且n→∞时,,而q<2017,说明数列在有限项后必定小于2017,设,且数列{M n}也为单调递减数列,M1≥0.根据以上分析:数列中必有一项(设为第k项),(其中M k≥0,且M k+1<0)∴=2017n+M1+M2+…+M k+M k+1+…+M n(∵{M n}为单调递减数列)≤2017n+kM1+M k+1+…+M n≤2017n+kM1+(n﹣k)M k+1,当n→∞时,kM1+(n﹣k)M k+1<0,∴,∴q∈[2016,2017)时,不满足条件.综上所得:q min=2017.。

2014-2015学年重庆市巴蜀中学高一(下)期末数学试卷(文科)一、选择题(共12小题,每小题5分,满分60分)1.(5分)已知向量=(2,1),=(x,﹣2),若∥,则x等于()A.1 B.﹣1 C.4 D.﹣42.(5分)等差数列{a n}中,若a1+a2015=4,则a2+a2014=()A.2 B.4 C.8 D.163.(5分)已知△ABC中,b=2,B=45°,C=105°,则a=()A.B.+1 C.﹣1 D.4.(5分)实数a,b,“<<0“是“a>b“的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件5.(5分)已知f′(x)是函数f(x)的导数,y=f′(x)的图象如图所示,则y=f (x)的图象最有可能是图中()A.B.C.D.6.(5分)若变量x,y满足约束条件,则2x+y的最大值是()A.2 B.4 C.7 D.87.(5分)在△ABC中,若,则△ABC是()A.等边三角形B.锐角三角形C.钝角三角形D.直角三角形8.(5分)已知点p(x,y)(x>0,y>0)在经过点A(2,0),B(0,1)两点的直线上,则+的最小值为()A.9 B.4 C.D.9.(5分)如图所示的程序框图运行的结果是()A.B.C.D.10.(5分)过点M(1,3)引圆x2+y2=2的切线,切点分别为A,B,则sin∠AMB=()A.B.C.D.11.(5分)已知||=2,是单位向量,且关于x的函数f(x)=x3+||x2+•x 是R上的单调函数,则向量与的夹角的范围是()A.[0,)B.[0,]C.[0,]D.[,)12.(5分)设函数f(x)=e x(2x﹣1)﹣ax+a对任意的x∈(﹣1,0)不等式f (x)<0恒成立,则a的范围是()A.(﹣∞,] B.[,1]C.(﹣∞,1]D.[,+∞)二、填空题(共4小题,每小题5分,满分20分)13.(5分)圆x2+y2﹣2x﹣2y=0的圆心坐标为.14.(5分)在△ABC中,角A的平分线为AD,D在边BC上,AB=,AD=,B=45°,则A=.15.(5分)数列{a n}满足a1=1,S n为{a n}前n项和,且2a n=S n+1,则+++…+=.16.(5分)圆O半径为2,A是圆O上一定点,BC是圆O上动弦,且弦长为3,则(+)•的最大值为.三、解答题(共6小题,满分70分)17.(10分)公差不为零的等差数列{a n},a2=4,且a2,a4,a7成等比数列.(1)求数列{a n}的通项a n;(2)设b n=+a n,求数列{b n}的前n项和T n.18.(12分)已知函数f(x)=ax3+cx在x=3处的切线方程为8x﹣y﹣18=0.(1)求函数f(x)的解析式;(2)若f(x)≤m(m∈R)对任意x∈[﹣2,2]上恒成立,求m的取值范围.19.(12分)已知直线l:kx﹣y+2k=0(k∈R)过定点为P.(1)若直线l与直线2015x+2015y﹣2017=0垂直,求k的值;(2)已知点A(1,3),B(﹣5,5),求过点P且与A,B点距离相等的直线l 的方程.20.(12分)在△ABC中,且a,b,c分别是内角A,B,C的对边,且a=bcosC ﹣c.(1)求角B的大小;(2)若△ABC的面积S=4,求△ABC周长的最小值.21.(12分)已知圆心为(2,3)的圆C上的点到直线x+y﹣3=0的最短距离为﹣1.(1)求圆C的方程;(2)过点N(﹣1,0)的直线l与圆C交于P,Q两点,且•=12,其中O 为坐标原点,求△OPQ的面积.22.(12分)设f(x)=﹣2ln(x+1)+x2﹣a(x﹣2)(a∈R).(1)当a=0时,求f(x)的单调区间和极值;(2)若存在唯一整数x0使f(x0)<0,求a的取值范围.2014-2015学年重庆市巴蜀中学高一(下)期末数学试卷(文科)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)已知向量=(2,1),=(x,﹣2),若∥,则x等于()A.1 B.﹣1 C.4 D.﹣4【解答】解:向量=(2,1),=(x,﹣2),若∥,则有1×x=2×(﹣2)=﹣4;即x=﹣4;故选:D.2.(5分)等差数列{a n}中,若a1+a2015=4,则a2+a2014=()A.2 B.4 C.8 D.16【解答】解:由等差数列{a n}的性质可得:a2+a2014=a1+a2015=4,故选:B.3.(5分)已知△ABC中,b=2,B=45°,C=105°,则a=()A.B.+1 C.﹣1 D.【解答】解:∵△ABC中,b=2,B=45°,C=105°,可得:A=180°﹣B﹣C=30°,∴由正弦定理,可得:a===.故选:A.4.(5分)实数a,b,“<<0“是“a>b“的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【解答】解:由“<<0“能推出“a>b“,是充分条件,由a>b推不出“<<0“,不是必要条件,故选:A.5.(5分)已知f′(x)是函数f(x)的导数,y=f′(x)的图象如图所示,则y=f (x)的图象最有可能是图中()A.B.C.D.【解答】解:根据导函数可知函数在(﹣∞,﹣1)上单调减,在(﹣1,1)上单调增,在(1,+∞)上单调减,结合图象可知y=f(x)的图象最有可能是图中B故选:B.6.(5分)若变量x,y满足约束条件,则2x+y的最大值是()A.2 B.4 C.7 D.8【解答】解:满足约束条件的可行域如下图中阴影部分所示:∵目标函数Z=2x+y,∴Z O=0,Z A=4,Z B=7,Z C=4,故2x+y的最大值是7,故选:C.7.(5分)在△ABC中,若,则△ABC是()A.等边三角形B.锐角三角形C.钝角三角形D.直角三角形【解答】解:由题意可知向量与的夹角为A,记||=c,||=b,||=a 则由可得,c2=bc•cosA+a2,即cosA=又由余弦定理可得cosA=,故=化简可得c2=a2+b2,由勾股定理可知△ABC为直角三角形.故选:D.8.(5分)已知点p(x,y)(x>0,y>0)在经过点A(2,0),B(0,1)两点的直线上,则+的最小值为()A.9 B.4 C.D.【解答】解:由A(2,0)、B(0,1)可求直线AB的斜率k AB==﹣,∴由点斜式可得直线AB的方程为:x+2y=2,∴+=(+)(x+2y)=(1+4++)≥(5+2)=(5+4)=,当且仅当x=,y=时取等号,故选:C.9.(5分)如图所示的程序框图运行的结果是()A.B.C.D.【解答】解:模拟程序的运行,可得A=0,i=1满足条件i≤1008,执行循环体,A=,i=2满足条件i≤1008,执行循环体,A=+,i=3…满足条件i≤1008,执行循环体,A=++…+=(1﹣﹣+…+﹣)=(1﹣)=,i=1009此时,不满足条件i≤1008,退出循环,输出A 的值为.故选:D.10.(5分)过点M(1,3)引圆x2+y2=2的切线,切点分别为A,B,则sin∠AMB=()A.B.C.D.【解答】解:如图所示,由题意可得|OM|==,|OB|=r=;由勾股定理可得|MA|=|MB|==2,∴sin∠OMB===,∴cos∠OMB===,∴sin∠AMB=sin2∠OMB=2sin∠OMBcos∠OMB=2××=.故选:C.11.(5分)已知||=2,是单位向量,且关于x的函数f(x)=x3+||x2+•x 是R上的单调函数,则向量与的夹角的范围是()A.[0,)B.[0,]C.[0,]D.[,)【解答】解:设向量与的夹角为θ∵函数f(x)=x3+||x2+•x是R上的单调函数,∴f′(x)=x2+||x+•与x轴没有交点或者只有一个交点,∴△=||2﹣4•=12﹣8cosθ≤0,即cosθ≥,∵0≤θ≤π,∴0≤θ≤,故选:B.12.(5分)设函数f(x)=e x(2x﹣1)﹣ax+a对任意的x∈(﹣1,0)不等式f (x)<0恒成立,则a的范围是()A.(﹣∞,] B.[,1]C.(﹣∞,1]D.[,+∞)【解答】解:对任意的x∈(﹣1,0)不等式f(x)<0恒成立,即a<在(﹣1,0)恒成立,令g(x)=,x∈(﹣1,0),则g′(x)=<0,故g(x)在(﹣1,0)递减,故a≤g(0)=1,故选:C.二、填空题(共4小题,每小题5分,满分20分)13.(5分)圆x2+y2﹣2x﹣2y=0的圆心坐标为(1,1).【解答】解:圆x2+y2﹣2x﹣2y=0,即圆(x﹣1)2+(y﹣1)2 =2,故它的圆心为(1,1),故答案为:(1,1).14.(5分)在△ABC中,角A的平分线为AD,D在边BC上,AB=,AD=,B=45°,则A=30°.【解答】解:角A的平分线为AD,D在边BC上,AB=,AD=,B=45°,△ABD中,由正弦定理,,可得:sin∠ADB=,∴∠ADB=60°或120°当∠ADB=60°时,那么:∠BAD=180°﹣45°﹣60°=75°,∴A=2∠BAD=150°,可得∠C=180﹣150°﹣45°=﹣15°不成立.故得∠ADB=120°,那么:∠BAD=180°﹣120﹣60°=15°,∴A=2∠BAD=30°,故答案为:30°.15.(5分)数列{a n}满足a1=1,S n为{a n}前n项和,且2a n=S n+1,则+++…+=2﹣()n﹣1.【解答】解:∵2a n=S n+1,)=S n+1,∴2(S n﹣S n﹣1+1),∴S n+1=2(S n﹣1∵S1+1=a1+1=2,∴数列{S n+1}是以2为首项,以2为公比的等比数列,∴S n+1=2×2n﹣1,∴a n=2n﹣1,∴=()n﹣1,∵=1∴+++…+==2﹣()n﹣1,故答案为:2﹣()n﹣116.(5分)圆O半径为2,A是圆O上一定点,BC是圆O上动弦,且弦长为3,则(+)•的最大值为12.【解答】解:如图,(+)•===.∴当与成0°角时,(+)•有最大值为2×2×3×1=12.故答案为:12.三、解答题(共6小题,满分70分)17.(10分)公差不为零的等差数列{a n},a2=4,且a2,a4,a7成等比数列.(1)求数列{a n}的通项a n;(2)设b n=+a n,求数列{b n}的前n项和T n.【解答】解:(1)由题意,{a n}是等差数列,设公差为d,a2=4,且a2,a4,a7成等比数列,则a4=4+2d,a7=4+5d,∴(4+2d)2=4(4+5d),解得:d=0(舍去)或d=1.∴通项a n=a2+(n﹣2)d=n+2.(2)b n=+a n,可得b n=2n+n+2.那么:{b n}的前n项和T n=T1+T2+…+T n=21+3+22+4+…+2n+n+2=21+22+…+2n+(3+4+5+…+n+2)==.18.(12分)已知函数f(x)=ax3+cx在x=3处的切线方程为8x﹣y﹣18=0.(1)求函数f(x)的解析式;(2)若f(x)≤m(m∈R)对任意x∈[﹣2,2]上恒成立,求m的取值范围.【解答】解:(1)f′(x)=3ax2+c,k=f′(3)=27a+c=8,①f(3)=27a+3c=8×3﹣18=6,②联立①②解得:,c=﹣1.∴f(x)=x3﹣x;(2)f(x)≤m(m∈R)对任意x∈[﹣2,2]上恒成立,即f(x)max≤m,x∈[﹣2,2]恒成立,f′(x)=x2﹣1,由f′(x)=x2﹣1=0,得x1=﹣1,x2=1.列x、f′(x)、f(x)的关系表:由表可知,.∴.19.(12分)已知直线l:kx﹣y+2k=0(k∈R)过定点为P.(1)若直线l与直线2015x+2015y﹣2017=0垂直,求k的值;(2)已知点A(1,3),B(﹣5,5),求过点P且与A,B点距离相等的直线l的方程.【解答】解:直线l:kx﹣y+2k=0(k∈R)化为:k(x+2)﹣y=0,令,解得x=﹣2,y=0,可得直线l过定点P(﹣2,0).(1)∵直线l与直线2015x+2015y﹣2017=0垂直,则k×=﹣1,解得k=1.(2)分类讨论:①若直线l∥AB,则k=k AB==﹣,可得直线l的方程为:﹣x﹣y﹣=0,化为:x+3y+2=0.②若直线l经过线段AB的中点M(﹣2,4),∴﹣2k﹣4+2k=0,无解,综上可得:直线l的方程为:x+3y+2=0.20.(12分)在△ABC中,且a,b,c分别是内角A,B,C的对边,且a=bcosC ﹣c.(1)求角B的大小;(2)若△ABC的面积S=4,求△ABC周长的最小值.【解答】解:(1)∵a=bcosC﹣c,∴由正弦定理可得:sinA=sinBcosC﹣sinC,可得:sin(B+C)=sinBcosC﹣sinC,∴sinBcosC+cosBsinC=sinBcosC﹣sinC,可得:cosBsinC=﹣sinC,∵C为三角形内角,sinC>0,可得:cosB=﹣,∴由B∈(0,π),可得:B=.(2)∵S=acsinB=×ac×=4,解得:ac=16,△ABC∴由余弦定理可得:cosB=≥,∴可得:≥,可得:﹣16≥32﹣b2,解得:b2≥48,即b≥4,当且仅当a=c=4时等号成立,∴△ABC周长=a+b+c=(a+c)+b≥2+b=2+4=8+4,即当a=c=4时,△ABC周长的最小值为8+4.21.(12分)已知圆心为(2,3)的圆C上的点到直线x+y﹣3=0的最短距离为﹣1.(1)求圆C的方程;(2)过点N(﹣1,0)的直线l与圆C交于P,Q两点,且•=12,其中O 为坐标原点,求△OPQ的面积.【解答】解:(1)设圆的方程是(x﹣2)2+(y﹣3)2=r2,(r>0),∵圆心为(2,3)到直线x+y﹣3=0的距离d1=,且圆心为(2,3)的圆C上的点到直线x+y﹣3=0的最短距离为﹣1,故r=1,故圆的方程是(x﹣2)2+(y﹣3)2=1;(2)当直线l的斜率不存在或斜率是0时,直线和圆相离,不合题意,从而直线的斜率必存在且不是0,设直线l的方程为x=my﹣1,且P(x1,y1),Q(x2,y2),则,消去x化简得:(m2+1)y2﹣(6m+6)y+17=0,故,∴x1x2=(my1﹣1)(my2﹣1)=m2y1y2﹣m(y1+y2)+1=,∴•=x1x2+y1y2==12,解得:m=1,满足△>0,故直线l的方程是:x=y﹣1即x﹣y+1=0,故该直线过圆心C(2,3),∴|PQ|=2r=2,又原点到直线l的距离为d=,故△OPQ的面积是S=|PQ|•d2=.22.(12分)设f(x)=﹣2ln(x+1)+x2﹣a(x﹣2)(a∈R).(1)当a=0时,求f(x)的单调区间和极值;(2)若存在唯一整数x0使f(x0)<0,求a的取值范围.【解答】解:(1)当a=0时,f(x)=﹣2ln(x+1)+x2,f′(x)=﹣=(x>﹣1),∴当x∈(﹣1,1)时,f′(x)<0,f(x)为减函数,当x∈(1,+∞)时,f′(x)>0,f(x)为增函数,∴当x=1时,函数f(x)求得极小值为f(1)=;(2)存在唯一整数x0使f(x0)<0,即存在唯一整数x0使<0,也就是a(x0﹣2)>,令g(x)=﹣2ln(x+1)+,h(x)=a(x﹣2).由(1)可知,x∈(﹣1,1)时,g(x)为减函数,当x∈(1,+∞)时,g(x)为增函数,且极小值为.∵ln(x+1)<x(x>0),∴g(x)=﹣2ln(x+1)+>,作出函数g(x)与h(x)的图象如图:要使存在唯一整数x0使f(x0)<0,则,则ln2﹣﹣4ln2+.∴a的取值范围是ln2﹣﹣4ln2+.。
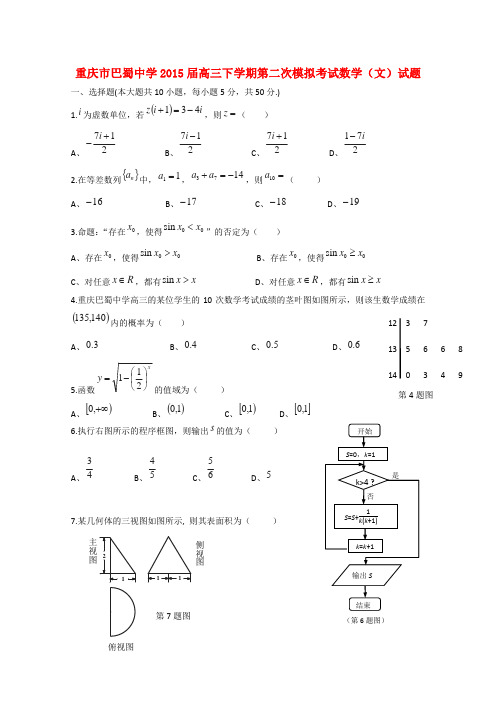
(第6题图)重庆市巴蜀中学2015届高三下学期第二次模拟考试数学(文)试题一、选择题(本大题共10小题,每小题5分,共50分.) 1.i 为虚数单位,若()i i z 431-=+,则=z ( )A 、217+-i B 、217-i C 、217+i D 、271i-2.在等差数列{}n a 中,11=a ,1473-=+a a ,则=10a ( )A 、16-B 、17-C 、18-D 、19- 3.命题:“存在0x ,使得0sin x x <”的否定为( )A 、存在x ,使得0sin x x > B 、存在x ,使得00sin x x ≥C 、对任意R x ∈,都有x x >sinD 、对任意R x ∈,都有x x ≥sin4.重庆巴蜀中学高三的某位学生的10次数学考试成绩的茎叶图如图所示,则该生数学成绩在()140,135内的概率为( )A 、3.0B 、4.0C 、5.0D 、6.0 5.函数xy ⎪⎭⎫ ⎝⎛-=211的值域为( ) A 、[)+∞,0 B 、()1,0 C 、[)1,0 D 、[]1,0 6.执行右图所示的程序框图,则输出s 的值为( )A 、43B 、54C 、65D 、57.某几何体的三视图如图所示, 则其表面积为( )12 3 713 5 6 6 814 0 3 4 9 (第4题图)第4题图主视图第7题图侧视图俯视图A 、225+πB 、3215++π C 、325+πD 、2215++π8.已知双曲线12222=-by ax()0,0>>b a ,右焦点为F ,过F 作一条渐近线的垂线,垂足为M ,O 为坐标原点,若OMF ∆面积为283c(其中c 为半焦距),则该双曲线离心率可能为( )A 、3B 、332 C 、3 D 、329.已知0,0>>b a 且1≠a ,若函数xy a log =过点()0,2b a +,则b a 111++的最小值为( )A 、2223+ B 、314C 、415D 、2210.设函数2()f x ax bx c =++(0a ≠),()f x 的导函数为()f x ',集合{}|()0A x f x =>,{}|()0B x f x '=>.若AB B =,则( )A 、20,40a b ac >-≥ B 、20,40a b ac >-≤ C 、20,40a b ac <-≥ D 、20,40a b ac <-≤二、填空题(本大题共5小题,每小题5分,共25分.)11.已知集合{}5,4,3,2,1=A ,{}6,4,2=B ,则)(B A C A =_____________.12.已知(1,2)a=,()4,2b=,设a ,b 的夹角为θ,则=θcos ___________.13.连续抛掷一枚硬币三次,则出现两次正面一次反面的概率为_____________.14.函数()2sin(),(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则=)3(πf .14题图15.已知圆C 的方程为1)4()3(22=-+-y x ,过直线l :053=-+ay x (0a >)上的任意一点作圆C 的切线,若切线长的最小值为15,则直线l 的斜率为__________.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分13分) 已知数列{}n a 为等差数列,{}n a 的前n 项和为nS ,11=a ,93=S .(1)求na 与nS ;(2)若数列{}n b 为等比数列,且11a b =,22a b =,求n b 及数列{}n b 的前n 项和n T.17.(本小题满分13分) 某工厂对同时生产某件产品的件数x (单位:件)与所用时间y (单位:小时)进行了测验.测验结果如下表所示: 求出y 与x 的线性回归方程a bx y +=ˆ;(2)试预测同时生产20件该产品需要多少小时?(附:线性回归方程a bx y +=ˆ中,1122211()()()nnii iii i nni i i i xx y y x ynx yb x x x nx====---==--∑∑∑∑,a y bx =-)18.(本小题满分13分) 已知函数2()ln f x x a xx=-+在点()1,(1)f 处的切线平行于x 轴.(1)求a 的值;(2)求()f x 的单调区间与极值.19.(本小题满分12分) 已知)3sin(sin )(π++=x x x f .求)(x f 的单调递增区间;(2)在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,若33)6(=-πA f ,AB 2=,2=a ,求边b ,c 的长.20.(本小题满分12分) 如图,四棱锥ABCD P -中,⊥PA 平面ABCD ,四边形ABCD 为直角梯形,DC AD ⊥,AB DC //,2==AB PA ,1==DC AD . (1)求证:BC PC ⊥;(2)E 为PB 中点,F 为BC 中点,求四棱锥EFCP D -的体积.20题图21.(本小题满分12分)已知椭圆22221x ya b+=(0a b>>)过M N、两点,O为坐标原点.求椭圆的标准方程;是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆恒有两个交点A B、且OA OB⊥?若存在,求出该圆的方程;若不存在,说明理由.18.解:(1)22222()1a x ax f x xxx++'=++=(()0,x ∈+∞)(1)30,3f a a '∴=+=∴=-(2)由(1)知,22232(1)(2)()x x x x f x xx-+--'==(()0,x ∈+∞)则()0f x '=的两根为121,2x x ==在()()0,12,+∞和上()0f x '>;在()1,2上()0f x '<.所以,()f x 的单调增区间为()()0,12,+∞和;单调减区间为()1,2.()f x 在11x =处取得极大值()(1)1f x f ==-极大; ()f x 在22x =处取得极小值()(2)13ln 2f x f ==-极小.19.解:(1)()sin sin()3f x x x π=++)6x π=+22222,26233k x k k x k k Zπππππππππ∴-≤+≤+-≤≤+∈即()f x ∴的单调增区间为22,2,33k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦.(2)02,02B A A ππ<=<∴<<又11()sin sin6326f A A A ππ-==∴=<=0,0,cos sin sin 22sin cos 63A B A B A A A ππ∴<<<<====723cos ,sin sin()927B C A B ∴===+=,则由正弦定理知:sin sin 46sin sin 9B C b ac aAA====.20.解:(1),,PA ABCD BC ABCD PA BC⊥⊂∴⊥面面连接,,,AC AD CD AD CD AC =⊥∴=,又2222BC AB AB AC BC BC AC ===+∴⊥,即,,,BC PAC PC PAC PC BC ∴⊥⊂∴⊥面又面.(2)由题可知3144EFCP PBC D EFCP PC BC S S V -====∴=21.解:(1)将M N 、两点代入椭圆方程,解之得:228,4a b ==,则椭圆的标准方程为:22184xy+=(2)存在这样的圆.(理由如下:) 设圆的半径为r ,圆的方程为222x y r+=,圆的切线与椭圆的交点为:()()1122,,,A x y B x y① 当圆的切线斜率k 存在时,设切线方程为:y kx b =+,则圆心到直线的距离为222,(1)d r b r k ===+即又切线与椭圆相交于两点A B 、,则有22184y kx b x y=+⎧⎪⎨+=⎪⎩,消去y 即可得:222(21)4280k x kbx b +++-=,由韦达定理有:12221224212821kb x x k b x x k ⎧+=-⎪⎪+⎨-⎪⋅=⎪+⎩,又OA OB⊥,则2212121212(1)()x x y y k x x kb x x b+=++++2222222222222222(28)(1)4(21)2121213883(1)8(1)2121b k b kb k k k k b k r k k k k -++=-++++--+-+===++283r ∴=②当斜率k 不存在时,切线方程为x r =±,由OA OB ⊥可知283r =综上所述,存在这样的圆,且圆的方程为2283x y +=.∘,PA ABCD BC ABCD⊥⊂面面PA BC ∴⊥ 连接AC ,,AD CD AD CD=⊥2222AC BC AB AB AC BC ∴====+,即,BC ACBC PAC PC PACPC BC∴⊥∴⊥⊂∴⊥面又面(2)34EFCP PBC PC BC S S ====,14D EFCP V -=21.解:(1)将M N 、两点,解之228,4a b ==,则椭圆的方程为:22184xy+=(2)当圆的切线斜率k 存在时,设切线方程为y kx b =+,圆的半径为r ,切线与椭圆的交点为()()1122,,,A x y B x y,则圆心到直线的距离为d r==,即222(1)b r k =+又切线与椭圆相交于两点,则有:22184y kx bx y=+⎧⎪⎨+=⎪⎩,消去y 即为222(21)4280k x kbx b +++-=,由韦达定理有:12221224212821kb x x k b x x k ⎧+=-⎪⎪+⎨-⎪⋅=⎪+⎩又OA OB⊥,则2212121212(1)()x x y y k x x kb x x b+=++++222222222(28)(1)4(21)212121b k b kb k k k k -++=-++++22222223883(1)8(1)2121b k r k k k k --+-+===++283r ∴=当斜率k 不存在时,切线方程为x r =,由0OA OB ⋅=可知283r =综上所述,存在这样的圆,且圆的方程为228=3x y +。

重庆市第一中学2015-2016学年高一数学下学期期末考试试卷(含解析)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) (1)已知集合,,则( )(A ) (B )(C ) (D )【答案】D 【解析】 试题分析:因,故,选D.考点:集合的运算.(2)设a =,b =(3,1),若ab ,则实数k 的值等于( )(A )-32(B )-53(C )53(D )32【答案】A 【解析】 试题分析:因,故,即,也即,选A.考点:向量的乘法运算.(3)设等差数列{a n }的前n 项和为S n ,若a 5+a 14=10,则S 18等于( ) (A )20 (B )60 (C )90(D )100 【答案】C考点:等差数列的通项及前项和.(4)圆与圆的位置关系为()(A)内切(B)相交(C)外切(D)相离【答案】B【解析】试题分析:因两圆心距,而,故两圆的位置关系相交,选B.考点:两圆的位置关系.(5)已知变量x,y满足约束条件,则z=3x+y的最大值为()(A)12 (B)11 (C)3 (D)-1【答案】BP(3,2)y=-3x+z-1x-y-1=0x+y-1=0y=2211Oyx考点:线性规划的知识及运用.(6)已知等比数列{a n }中,a 1=1,q =2,则T n =1a1a2+1a2a3+…+1anan +1的结果可化为( )(A )1-14n (B )1-12n (C )23(1-14n )(D )23(1-12n )【答案】C 【解析】 试题分析:因成等比数列,且公比为,故,选C.考点:等比数列的通项及前项和的综合运用.(7)“m =1”是“直线与直线平行”的( )(A )充分不必要条件 (B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件【答案】C 【解析】考点:充分必要条件.(8)阅读右面的程序框图,运行相应的程序,输出S的值为()(A)15 (B)105(C)245 (D)945【答案】B【解析】试题分析:依据算法流程图中提供的信息可以看出当时,就结束算法,所以,选B.考点:算法流程图的识读.(9)现有两组卡片,第一组卡片上分别写有数字“2,3,4”,第二组卡片上分别写有数字“3,4,5”,现从每组卡片中各随机抽出一张,用抽取的第一组卡片上的数字减去抽取的第二组卡片上的数字,差为负数的概率为()(A ) (B ) (C )(D )【答案】D 【解析】考点:古典概型的计算公式及运用.(10)在平行四边形ABCD 中,AD =2,∠BAD =60°,E 为CD 的中点,若AD →BE →=1,则AB 的长为( )(A ) 6 (B )4 (C )5 (D )6 【答案】A 【解析】 试题分析:因,即,也即,故选A.考点:向量的几何运算.【易错点晴】本题设置的目的是综合考查向量的几何运算形式和向量数量积公式.求解时充分借助题设条件,运用向量的三角形法则,应用向量的数量积公式建立关于所求未知量的方程.解答本题的关键是如何运用已知向量合理表示,也是解答本题的难点.求解时容易出错的地方是不能合理地运用向量的相等和等价代换,从而陷入问题求解的困境.(11)(原创)已知函数,且对于任意实数关于的方程都有四个不相等的实根,则的取值范围是( ) (A )(B )(C )(D )【答案】C 【解析】x 4x 3x 2x 1BA x=m-1y=a11Oyx考点:函数方程的关系及数形结合的数学思想的综合运用.【易错点晴】本题综合考察了函数的零点和函数的图象和性质等多个知识点,求解时充分借助题设条件,准确地画出函数的图象,依据题设和图像的有效信息,先算出抛物线的顶点到轴的距离,即,由于,所以必须满足,解之得.也就是确定了参数的取值范围.又由于四个零点满足,所以,因此问题转化为求参数的取值范围.(12)(原创)已知集合,,若,则的最小值( )(A )45 (B )34(C )(6-25)(D )54【答案】A 【解析】考点:等价转化的数学思想和数形结合的思想.【易错点晴】本题以两个点集合的交集非空等有关知识为背景,设置了一道求的最值为目的的综合问题.解答时先将问题进行等价转化和化归,即转化为直线与圆有交点的前提下,求的最小值的问题.如果直接求解相当困难,在这里运用数形结合的数学思想进行求解.先考虑坐标原点到定直线的距离是定值.注意到动圆经过坐标原点,所以移动动圆,当圆心在的中点时,既满足题设条件又能取到最小值,使得问题简捷巧妙获解. 第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每题5分,满分20分.) (13)某学校高一、高二、高三年级的学生人数之比为,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高一年级抽取 名学生. 【答案】【解析】试题分析:应从高一年级学生中抽取名学生,故应填.考点:分层抽样及运用.(14)(原创)在中,角所对边长分别为,若,则b=___________.【答案】考点:正弦定理及运用.(15)已知点P,Q为圆C:x2+y2=25上的任意两点,且|PQ|<6,若PQ中点组成的区域为M,在圆C内任取一点,则该点落在区域M上的概率为__________ .【答案】【解析】试题分析:设的中点为,由于,则由题设,即点在以为圆心,半径为的圆外,已知圆内的区域,所以由几何概型的概率公式可得其概率为,故应填.考点:几何概型及运用.【易错点晴】本题是一道几何概型的计算问题.解答时,充分借助题设条件,巧妙地运用了这样一个结论:在平面上到一个定点距离等于定值的点的轨迹是以这个定点为圆心,定值为半径的圆.求解的过程中,依据弦长越小,则圆心距则越大这一事实很容易获得了.其实是这样的:因,然后算得,所以由几何概型的概率的计算公式可得其概率.(16)(原创)点C是线段..AB上任意一点,O是直线AB外一点,,不等式对满足条件的x,y恒成立,则实数k的取值范围____.【答案】【解析】考点:不等式恒成立的条件及判别式求最值和值域.【易错点晴】本题在解答时应用了一个平面向量中的一个重要结论:若点是线段上的一点,是直线外一点且,则.证明如下:由共线定理可得,即,由此可得,即,也即,所以.解答本题时,先将参数分离出来,再构造函数求其最小值.求最小值时运用的是判别式法,而且上述过程中的.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)(17)(本小题满分10分)已知的面积是3,角所对边长分别为,.(Ⅰ)求;(Ⅱ)若,求的值.【答案】(Ⅰ);(Ⅱ).【解析】考点:正弦定理余弦定理的综合运用.(18)(本小题满分12分)已知圆:,直线l过定点.(Ⅰ)若l与圆相切,求直线l的方程;(Ⅱ)若l与圆相交于、两点,且,求直线l的方程.【答案】(Ⅰ)或;(Ⅱ)或.【解析】试题分析:(Ⅰ)对斜率的存在和不存在进行分类再运用点到直线的距离公式建立方程求解;(Ⅱ)借助题设条件运用点到直线的距离公式建立方程求解.试题解析:(Ⅰ)当斜率不存在时,方程x=1满足条件;当L1斜率存在时,设其方程是y=k(x-1),则,解得,所以所求方程是x=1和3x-4y-3=0;考点:直线与圆的位置关系及综合运用.【易错点晴】本题考查和检测是直线与圆的位置关系的基础知识和基本方法.求解时充分借助题设条件,运用了直线与圆相切的条件和直线与圆相交所截得的弦长的条件求出满足题设条件的直线的方程.需要强调的是:本题在设置时,特别注意到直线的点斜式的运用的条件问题,当直线的斜率存在时,可以运用直线的点斜式方程;若直线的斜率不存在,则不能运用直线的点斜式方程,但直线的方程还是存在的,即是这是许多学生容易忽视的地方.(19)(本小题满分12分)某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:40,50),50,60),…,90,100]后得到如图所示的频率分布直方图.(Ⅰ)若该校高一年级共有学生640名,试估计该校高一年级期中考试数学成绩不低于60分的人数;(Ⅱ)若从数学成绩在40,50)与90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.【答案】(Ⅰ);(Ⅱ).【解析】试题分析:(Ⅰ)先求频率再依据频率频数的关系求解;(Ⅱ)借助题设条件运用列举法和古典概型公式求解.试题解析:(Ⅰ)根据频率分布直方图,成绩不低于60分的频率为1-10×(0.005+0.01)=0.85.由于该校高一年级共有学生640名,利用样本估计总体的思想,可估计该校高一年级期中考试数学成绩不低于60分的人数约为640×0.85=544.(Ⅱ)成绩在40,50)分数段内的人数为40×0.05=2,成绩在90,100]分数段内的人数为40×0.1=4,则记在40,50)分数段的两名同学为A1,A2,在90,100]分数段内的同学为B1, B2,B3,B4.若从这6名学生中随机抽取2人,则总的取法共有15种.如果2名学生的数学成绩都在40,50)分数段内或都在90,100]分数段内,那么这2名学生的数学成绩之差的绝对值一定不大于10;如果一个成绩在40,50)分数段内,另一个成绩在90,100]分数段内,那么这2名学生的数学成绩之差的绝对值一定大于10.则所取2名学生的数学成绩之差的绝对值不大于10的取法有(A 1,A 2),(B 1,B 2),(B 1,B 3),(B 1,B 4),(B 2,B 3),(B 2,B 4),(B 3,B 4)共7种取法,所以所求概率为P =715.考点:频率的性质和古典概型公式的综合运用. (20)(本小题满分12分) 已知数列{a n }满足(其中).(Ⅰ)求数列{a n }的通项公式; (Ⅱ)设,其前n 项和是T n ,求证:T n <79.【答案】(Ⅰ);(Ⅱ)证明见解析.【解析】∴T n -T n =+++…+-=+-=-,∴T n =-<.考点:等差数列和等比数列的知识的综合运用.(21)(原创)(本小题满分12分)已知动点满足方程.(Ⅰ)求动点P到直线距离的最小值;(Ⅱ)设定点,若点之间的最短距离为,求满足条件的实数的取值.【答案】(Ⅰ) ;(Ⅱ)或.【解析】试题分析:(Ⅱ)设点(),则设(),则,设()对称轴为分两种情况:(1)时,在区间上是单调增函数,故时,取最小值∴,∴,∴(舍)(2)>时,∵在区间上是单调减,在区间上是单调增,∴时,取最小值∴,∴(舍)综上所述,或考点:函数的图象和性质或基本不等式的综合运用.(22)(本小题满分12分)已知函数为奇函数,且.(Ⅰ)求实数a与b的值;(Ⅱ)若函数,设为正项数列,且当时,,(其中),的前项和为,,若恒成立,求的最小值.【答案】(Ⅰ) ,;(Ⅱ).【解析】由:,恒成立,即:恒成立,当时,,再由复合函数单调性知,数列为单调递减数列,且时,,当时,中的每一项都大于,∴恒成立;当时,数列为单调递减数列,且时,而,说明数列在有限项后必定小于,设,且数列也为单调递减数列,。

一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知单位向量,a b 满足:23a b +=,则2a b -=( )A B C 【答案】D考点:向量的运算.2.已知1,,,,5a b c 五个数成等比数列,则b 的值为( )A .3B ..52【答案】B 【解析】试题分析:由题意得,215b b =⨯⇒=,又2210b q q =⨯=>,所以b =B . 考点:等比数列的性质.3.直线sin 20x θ++=的倾斜角的取值范围是( )A .5,66ππ⎡⎤⎢⎥⎣⎦ B .2,33ππ⎡⎤⎢⎥⎣⎦ C .50,,66πππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦ D .20,,33πππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦【答案】C 【解析】试题分析:由题意得,直线sin 20x θ++=的斜率为[k =,设直线的倾斜角为α,及tan [α∈,所以50,,66ππαπ⎡⎤⎡⎤∈⎢⎥⎢⎥⎣⎦⎣⎦,故选C . 考点:直线的斜率与倾斜角.4.在ABC ∆中,,,a b c 分别是三内角,,A B C 的对边,且()22sin sin sin sin sin A C A B B -=-,则角C 等于( ) A .6πB .3πC .56π D .23π【答案】B考点:正弦定理与余弦定理的应用.5.在ABC ∆中,内角,,A B C 所对应的边分别为,,a b c ,若sin cos 0b A B =,且,,a b c 成等比数列,则a cb+的值为( )A B C .2 D .4 【答案】C 【解析】试题分析:在ABC ∆中,由sin cos 0b A B -=,利用正弦定理得sin sin cos 0B A A B =,所以tan B =,得3B π=,由余弦定理得2222222cos ()3b a c ac B a c ac a c ac =+-=+-=+-,又,,a b c成等比数列,所以2b ac =,所以224()b a c =+,所以2a cb+=,故选C . 考点:正弦定理与余弦定理的应用.6. 在ABC ∆中,,,a b c 分别是三内角,,A B C 的对边,若sin cos cos A B Ca b c==,则ABC ∆是( ) A .等边三角形 B .有一内角是30°的三角形 C .等腰直角三角形 D .有一内角是30°的等腰三角形【答案】C 【解析】 试题分析:由sin cos cos A B Ca b c==,由正弦定理得2sin ,2sin ,2sin a R A b R B c R C ===,所以 cos cos 1sin sin B C B C ==,则tan tan 1B C ==,所以4B C π==,所以ABC ∆为等腰直角三角形,故选C . 考点:正弦定理的应用.7.设等差数列{}n a 的前n 项和为n S ,且满足201620170,0S S ><,对任意正整数n ,都有n k a a ≥,则k 的值为( )A .1006B .1007C .1008D .1009 【答案】D考点:等差数列的前n 项和的应用.【方法点晴】本题主要考查了等差数列的通项公式及其前n 项和公式的应用,不等式的性质,着重考查了学生分析解答问题的能力和转化与化归的思想方法,属于中档试题,本题的解答中,设等差数列{}n a 的公差为d ,利用等差数列的前n 项和公式,可得100810090,0,0a a d ><<,可得数列为递减数列,在利用n k a a ≥,即可求解k 的值.8.给出下列四个命题,其中正确的命题是( )①若()()()cos cos cos 1A B B C C A ---=,则ABC ∆是等边三角形; ②若sin cos A B =,则ABC ∆是直角三角形; ③若cos cos cos 0A B C <,则ABC ∆是钝角三角形; ④若sin 2sin 2A B =,则ABC ∆是等腰三角形;A .①②B .③④C .①③D .②④ 【答案】C考点:三角形状的判定.9.已知O 是三角形ABC 所在平面内一定点,动点P 满足()0sin sin AB AC OP OA AB B AC C λλ⎛⎫=++≥ ⎪⎝⎭,则P 点轨迹一定通过三角形ABC 的( )A .重心B .外心C .垂心D .内心 【答案】A 【解析】试题分析:作出如图的图形AD BC ⊥,由于sin sin AB B AC C AD ==,所以()sin sin AB AC OP OA OA AB AC AD AB B AC C λλ⎛⎫=++=++ ⎪⎝⎭,由加法法则知,P 在三角形的直线上,所以动点的轨迹一定经过ABC ∆的重心,故选A .考点:向量的运算及向量加法的几何意义. 10.设正数,x y 满足:,23x y x y >+=,则195x y x y+-+的最小值为( )A .83B .114C .4D .2 【答案】A考点:基本不等式的应用求最值.11.设数列{}n a 满足123121,4,9,,4,5,n n n a a a a a a n --====+=则2017a =( )A .8064B .8065C .8067D .8068 【答案】B 【解析】试题分析:由12n n n a a a --=+,可得11n n n a a a +-=+,两式作差得,112n n n a a a a +--=-,即112(4,5,)n n n a a a n +-=+=,所以数列{}n a 的奇数项与偶数项均构成等差数列,因为131,9a a ==,所以奇数项的公差为8d =,所以20171(20171)18(20171)8065a a d =+-=+-=,故选B . 考点:数列的递推式及等差数列的通项公式.【方法点晴】本题主要考查了数列的递推关系是等差数列的定义及其通项公式的应用,着重考查了数列的递推关系的化简、分析问题和解答问题的能力及转化与化归思想的应用,属于中档试题,本题的解答中由数列的递推关系式12n n n a a a --=+,可得112n n n a a a +-=+,即可说明数列{}n a 的奇数项与偶数项均构成等差数列,由等差数列的通项公式,即可求解结果.12.已知实数,,x y z 满足222234x y z ++=,设T xy yz =+,则T 的取值范围是( )A .⎡⎢⎣B .⎡⎢⎣C .⎡⎢⎣D .⎡⎢⎣【答案】D考点:基本不等式的应用.【方法点晴】本题主要考查了基本不等式的应用,其中正确构造基本不等式的应用条件是使用基本不等式的基础和关键,试题思维量大,运算繁琐,属于难题,着重考查了构造思想和转化与化归思想的应用,本题的解答中,设0,0αβ>>且2αβ+=,得()()222243x y yz αβ=+++,即可利用基本不等式,可求得m 的值,即可求解取值范围.第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每题5分,满分20分.)13.在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,已知030,2A b ==,如果这样的三角形有且只有一个,则a 的取值范围为________. 【答案】1a =或2a ≥ 【解析】试题分析:由题意得,在ABC ∆中内角,,A B C 所对的边分别为,,a b c ,由030,2A b ==,所以sin 1b A =,所以当2a b ≥=或1a =时,此时满足条件的三角形只有一个. 考点:正弦定理的应用. 14.有如下命题:①“0a b >>”是“11a b <”成立的充分不必要条件; ②0,0a b t >>>,则a a tb b t+<+;③552332a b a b a b +≥+对一切正实数,a b 均成立; ④“1ab>”是“0a b ->”成立的必要非充分条件. 其中正确的命题为___________.(填写正确命题的序号) 【答案】①③考点:不等式的性质及命题的真假判定.15.已知三角形ABC 中,过中线AD 的中点E 任作一条直线分别交边,AB AC 于,M N 两点,设(),0,0AM xAB AN y AC x y ==>>,则4x y +的最小值为___________.【答案】94【解析】试题分析:因为1()2AD AB AC =+且E 为AD 的中点,所以11()24AE AD AB AC ==+,又因为(),0,0AM xAB AN y AC x y ==>>,所以11,AB AM AC AN x y ==,所以111()4AE AM AN x y=+,又,,M E N 三点共线,所以111(0,0)44x y x y +=>>,于是114(4)()44x y x y x y+=++1191144444y x x y =+++≥++=.考点:平面向量的运算及基本不等式的应用.【方法点晴】本题主要考查了平面向量的运算及基本不等式的应用,中点考查了平面向量的加法运算、向量的共线及共面的基本定理,基本不等式求解最值等知识点,求解本题的关键在于构造基本不等式的条件,利用基本不等式求解最值,着重考查学生分析问题和解答问题的能力及运算推理能力,属于中档试题.16.已知数列{}n a 的前n 项和为n S 且()()()122212n n n n a n N n n n ++-=∈++,则n S =_________. 【答案】()()()12112n n S n N n n ++=-∈++考点:数列的求和.【方法点晴】本题主要考查了数列的求和及数列的递推式的化简、运算,其中正确化简数列的递推关系,合理裂项是解得此类问题的关键,试题思维量大,运算量大,难点多,有一定的难度,属于难题,着重考查了学生分析问题和解答问题的能力,本题的解答中,正确、合理化简数列的通项公式()()()()()112222212112n n n nn n a n n n n n n n ++-==-+++++是解答的关键. 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题 满分10分)已知4,8a b ==,a 与b 的夹角为23π. (1)求a b +;(2)求k 为何值时,()()2a b ka b +⊥-.【答案】(1)(2)7k =-. 【解析】试题分析:(1)由向量的模的计算公式,可化简得()22222a b a b a a b b +=+=++,即可求解;(2)根据()()2a b ka b +⊥-,所以()()20a bka b +-=,列出方程,即可求解.试题解析:(1)()2222121624864482a b a ba ab b ⎛⎫+=+=++=+-+= ⎪⎝⎭,所以43a b +=.(2)因为()()2a b ka b +⊥-,所以()()20a bka b +-=,即()222120ka k a b b +--=,即()()1621161280k k +---=,解得7k =-. 考点:向量的运算. 18.(本小题满分12分) 已知0,0a b >>,且122a b+=. (1)求ab 的最小值;(2)求2a b +的最小值,并求出a 、b 相应的取值. 【答案】(1)2;(2)32a b ==. 等号成立的充要条件是12222a bb aab ⎧+=⎪⎪⎨⎪=⎪⎩且0,0a b >>,即:32a b ==;∴2a b +的最小值为92;此时32a b ==.考点:基本不等式的应用求解最值. 19.(本小题满分12分)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,设S 为ABC ∆的面积,且)222S b c a =+-. (1)求角A 的大小;(2)若6a =,求ABC ∆周长的取值范围. 【答案】(1)3A π=;(2)(]12,18.考点:正项定理、余弦定理及三角形的面积公式. 20.(本小题满分12分)数列{}n a 满足()*13221,2,27nn n a a n N n a -=++∈≥=.(1)已知()()*12n n n b a t n N =+∈,若数列{}n b 成等差数列,求实数t ;(2)求数列{}n a 的前n 项和n S .【答案】(1)1t =;(2)()()*2121n n S n n n N =--+∈.()()()14123212212112n n n n n n n --=+-++=-++--.所以()()*2121n n S n n n N=--+∈. 解法二:(1)()()*12n n n b a t n N =+∈且数列{}n b 成等差数列,所以有()()*1n n b b n N +-∈为常数. ()()()*1111122n n n n n n b b a t a t n N +++-=+-+∈ ()()()()1*1*11122122111112222n n n n nn n n n n n a t a t n N t a a n N +++=+++-+∈+=++--∈ ()*1112n t n N +-=+∈,要使()()*1n n b b n N +-∈为常数,需1t =.考点:等差数列的定义及通项公式;数列求和.21.(本小题满分12分)在ABC ∆中,角,,A B C 所对的边分别为5,,,cos 13a b c B =-. (1)若2sin A 、sin B 、2sin C 成等比数列,613ABC S ∆=,求,a c 的等差中项; (2)若4cos ,145C AC AB ==,求a .【答案】(1;(2)114a =.考点:等差、等比数列的性质及其余弦定理的应用.【方法点晴】本题主要考查了等差数列与等比数列的通项及性质,涉及到三角形中正弦定理与余弦定理的应用,属于中档试题,着重考查了学生分析问题和解答问题的能力,本题的解答中利用正弦定理可把2sin 4sin sin B A C =,化为24b ac =,进而可求解a c +的值,同时计算出sin ,sin ,cos B C A 的值,代入题设条件,即可求解a 的值.22.(本小题满分12分)已知12a =,点()1,n n a a +在函数()22f x x x =+的图像上,其中*n N ∈. (1)证明:数列(){}lg 1n a +是等比数列;(2)记112n n n b a a =++,求数列{}n b 的前项和n S . 【答案】(1)证明见解析;(2)22131n n S =--.(2)由(1)式得1231n n a -=-,212n n n Qa a a +=+,∴()11n n n a a a +=+, ∴1111122n n n a a a +⎛⎫=- ⎪+⎝⎭,∴11122n n n a a a +=-+. 又112n n n b a a =++,∴1112n n n b a a +⎛⎫=- ⎪⎝⎭,∴1212231111111111122n n n n n S b b b a a a a a a a a ++⎛⎫⎛⎫=++=-+-++-=- ⎪ ⎪⎝⎭⎝⎭, ∵1221131,2,31n n n n a a a -+=-==-,∴22131nn S =--. 考点:等比数列的定义及数列的递推式;数列的求和.【方法点晴】本题主要考查了等比数的通项公式及其递推关系的化简、数列的求和问题,其中熟练掌握利用取对数法把已知转化为的等比数列问题的求解、等比数列的定义及通项公式,“裂项求和”法等是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题,本题的解答中,把数列{}n b 的通项公式合理裂项、准确计算是本题的一大易错点.四、附加题:本题满分15分,解答应写出必要的文字说明、证明过程或才演算步骤,本题所得分数计入总分.23. 已知数列{}n a 满足:()123,1a t t R t =-∈≠±,()()()112321121n n n n n n t a t t a n N a t +++-+--=∈+-. (1)求数列{}n a 的通项公式;(2)若0t >,试比较1n a +与n a 的大小. 【答案】(1)()211n n t a n -=-;(2)1n n a a +>.考点:等比数列的定义及数列的递推式的应用.。
2015-2016学年重庆市巴蜀中学高一(下)期末数学试卷一、选择题(共12×5=60分)1.直线的倾斜角为()A.B.C. D.2.圆x2+y2+2x+y=0的半径是()A.B.C.D.3.直线l1:mx﹣y=0与直线l2:x﹣my+4=0互相平行,则实数m的值为()A.1 B.﹣1 C.0 D.±14.函数y=(x>0)的最大值为()A.2 B.C.D.5.已知非零向量满足(+)⊥(﹣),且||=||,则向量与的夹角为()A.B.C.D.6.已知,则z=x﹣2y的取值范围是()A.[﹣8,12]B.[﹣4,12]C.[﹣4,4] D.[﹣8,4]7.△ABC中,角A、B、C所对的边分别是a、b、c,且c2﹣b2=ab,C=,则的值为()A.B.1 C.2 D.38.已知x1>x2>x3,若不等式恒成立,则实数m的最大值为()A.9 B.7 C.3+2D.1+9.递增的等差数列{a n}满足:a1+a2+a3=12,a1a2a3=63,S n是数列{a n}的前n项和,则使S n >2018的最小整数n的值为()A.80 B.84 C.87 D.8910.已知椭圆=1(a>b>0)的左顶点、上顶点、右焦点分别为A、B、F,且∠ABF=90°,则的值为()A.B.C.D.11.已知数列{a n}满足:a1=1,a n+1﹣a n=2n(n∈N*),数列b n=),T n=b1+b2+…+b n,则T10的值为()A. B. C.D.12.已知直线l与椭圆=1(a>b>0)相切于直角坐标系的第一象限的点P(x0,y0),且直线l与x、y轴分别相交于点A、B,当△AOB(O为坐标原点)的面积最小时,∠F1PF2=60°(F1、F2是椭圆的两个焦点),若此时∠F1PF2的内角平分线长度为a,则实数m的值是()A.B.C.D.二、填空题(共20分)13.已知x>y>0,则与中较大者是.14.△ABC中,角A、B、C所对的边分别为a、b、c,B=,sinA:sinC=4:3,且△ABC的面积为,则c=.15.等边△ABC的边长为2,且,则=.16.已知圆C的圆心在直线x+y﹣2=0上,圆C经过点(2,﹣2)且被x轴截得的弦长为2,则圆C的标准方程为.三、解答题(共70分)17.已知椭圆=1的左、右焦点分别为F1、F2,点P在该椭圆上.(1)求实数m的取值范围;(2)若m=5,且|PF1|=3,求点P到x轴的距离.18.△ABC中,角A、B、C所对的边分别为a、b、c,角A为锐角,且.(1)求角C的大小;(2)求sinA+sinB的取值范围.19.已知圆的方程为x2+y2﹣2x﹣2my+2m2﹣4m+1=0(m∈R).(1)当该圆的半径最长时,求m的值;(2)在满足(1)的条件下,若该圆的圆周上到直线l:2kx﹣2y+4+﹣3k=0的距离等于1的点有且只有3个,求实数k的值.20.已知S n是数列{a n}的前n项和,且a1=2,a n+1=3S n﹣2(n∈N*).(1)求数列{a n}的通项公式;(2)设b n=),求证,b1b2+b2b3+…+b n b n+1<3(n∈N*).21.已知椭圆C:=1(a>b>0)的离心率为,且点(2,)在C上.(1)求C的方程;(2)过点P(2,1)的直线l与椭圆C交于A,B两点,且AB的中点恰为P,求直线l的方程.22.已知椭圆C:=1(a>b>0)的两焦点F1、F2与短轴两端点构成四边形为正方形,又点M是C上任意一点,且△MF1F2的周长为2+2.(1)求椭圆C的方程;(2)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆E上一点,且满足(O为坐标原点),当|AB|<时,求实数t的取值范围.2015-2016学年重庆市巴蜀中学高一(下)期末数学试卷参考答案与试题解析一、选择题(共12×5=60分)1.直线的倾斜角为()A.B.C. D.【考点】直线的倾斜角.【分析】求出直线的斜率,从而求出直线的倾斜角即可.【解答】解:直线,即x+y=3,故直线的斜率是k=﹣,故倾斜角是:,故选:D.2.圆x2+y2+2x+y=0的半径是()A.B.C.D.【考点】圆的一般方程.【分析】化圆的方程为标准方程,即可求出半径.【解答】解:把圆x2+y2+2x+y=0化标准方程为:,则圆x2+y2+2x+y=0的半径是:.故选:B.3.直线l1:mx﹣y=0与直线l2:x﹣my+4=0互相平行,则实数m的值为()A.1 B.﹣1 C.0 D.±1【考点】直线的一般式方程与直线的平行关系.【分析】由直线与直线平行的性质得m≠0,且,由此能求出m的值.【解答】解:∵直线l1:mx﹣y=0与直线l2:x﹣my+4=0互相平行,∴m≠0,且,解得m=±1.故选:D.4.函数y=(x>0)的最大值为()A.2 B.C.D.【考点】函数的最值及其几何意义.【分析】将函数y化为6﹣(x+),由基本不等式a+b≥2(a,b>0,a=b取得等号),计算即可得到所求最大值.【解答】解:∵x>0,∴y====6﹣(x+)≤6﹣2=6﹣4=2,当且仅当x=即x=2时,取得最大值2.故选:A.5.已知非零向量满足(+)⊥(﹣),且||=||,则向量与的夹角为()A.B.C.D.【考点】平面向量数量积的运算.【分析】根据向量垂直的等价条件建立方程关系,结合数量积的应用进行求解即可.【解答】解:∵(+)⊥(﹣),且||=||,∴(+)•(﹣)=0,即2﹣2﹣•=0,即22﹣2﹣×|||cos<,>=0,则﹣×cos<,>=0,则cos<,>=,则<,>=,故选:A6.已知,则z=x﹣2y的取值范围是()A.[﹣8,12]B.[﹣4,12]C.[﹣4,4] D.[﹣8,4]【考点】简单线性规划.【分析】画出不等式组表示的平面区域,利用目标函数的几何意义求其最值.【解答】解:不等式组表示的平面区域如图,当直线y=x﹣经过图中B时z最大,经过D时z最小,又得到B(4,﹣4),由得到D(0,4),所以x﹣2y的最大值为4+2×4=12,最小值为0﹣2×4=﹣8;所以z=x﹣2y的取值范围是[﹣8,12];故选A.7.△ABC中,角A、B、C所对的边分别是a、b、c,且c2﹣b2=ab,C=,则的值为()A.B.1 C.2 D.3【考点】余弦定理;正弦定理.【分析】由于已知及余弦定理可解得a=2b,利用正弦定理即可得解.【解答】解:∵C=,∴由余弦定理可得:c2=a2+b2﹣2abcosC=a2+b2﹣ab,∵c2﹣b2=ab,∴a2+b2﹣ab=b2+ab,解得:a=2b,∴利用正弦定理可得:.故选:C.8.已知x1>x2>x3,若不等式恒成立,则实数m的最大值为()A.9 B.7 C.3+2D.1+【考点】数列与不等式的综合.【分析】通过变形可知问题转化为求+2•的最小值,进而利用基本不等式计算即得结论.【解答】解:∵x1>x2>x3,∴x1﹣x2>0,x2﹣x3>0,x1﹣x3>0,又∵,∴m≤(x1﹣x3)(+)=+2•=3++2•,∵+2•≥2=2,∴m≤3+2,故选:C.9.递增的等差数列{a n}满足:a1+a2+a3=12,a1a2a3=63,S n是数列{a n}的前n项和,则使S n >2018的最小整数n的值为()A.80 B.84 C.87 D.89【考点】等差数列的前n项和.【分析】由等差数列通项公式列出方程组,求出首项和公差,从而求出S n=,由此能求出使S n>2018的最小整数n的值.【解答】解:递增的等差数列{a n}满足:a1+a2+a3=12,a1a2a3=63,∴,解得,d=,=,∵S n>2018,∴>2018,∴n2+13n﹣8072>0,解得n>≈83.6,由n∈N*,∴使S n>2018的最小整数n的值为84.故选:B.10.已知椭圆=1(a>b>0)的左顶点、上顶点、右焦点分别为A、B、F,且∠ABF=90°,则的值为()A.B.C.D.【考点】椭圆的简单性质.【分析】利用椭圆的性质用a,b,c表示出△ABF的边长,利用勾股定理列方程得出a,b,c的关系.【解答】解:由椭圆的定义可知|AF|=a+c,|AB|=,|BF|=a,∵∠ABF=90°,∴|AB|2+|BF|2=|AF|2,即a2+b2+a2=a2+c2+2ac,∴a2+b2=c2+2ac.又b2=a2﹣c2,∴a2﹣c2﹣ac=0,即()2+﹣1=0,∴=,∴===.故选:D.11.已知数列{a n}满足:a1=1,a n+1﹣a n=2n(n∈N*),数列b n=),T n=b1+b2+…+b n,则T10的值为()A. B. C.D.【考点】数列的求和.【分析】利用累加法先求出数列{a n}的通项公式,利用数列的递推关系求出数列{b n}的通项公式,利用错位相减法进行求和即可.【解答】解:∵a1=1,a n+1﹣a n=2n(n∈N*),∴a2﹣a1=2,a3﹣a2=22,a4﹣a3=23,…a n﹣a n﹣1=2n﹣1,等式两边同时相加得:a n﹣a1=2+22+23+…2n﹣1,即a n=a1+2+22+23+…2n﹣1=1+2+22+23+…2n﹣1==2n﹣1,b n=)===,则T n=+++…+,①则T n=+++…++,②①﹣②得T n=+++…+﹣=﹣=1﹣()n﹣,则T n=2﹣﹣=2﹣.则T10=2﹣=2﹣=2﹣=.故选:B12.已知直线l与椭圆=1(a>b>0)相切于直角坐标系的第一象限的点P(x0,y0),且直线l与x、y轴分别相交于点A、B,当△AOB(O为坐标原点)的面积最小时,∠F1PF2=60°(F1、F2是椭圆的两个焦点),若此时∠F1PF2的内角平分线长度为a,则实数m的值是()A.B.C.D.【考点】椭圆的简单性质.【分析】由题意,切线方程为=1,利用基本不等式,结合△AOB(O为坐标原点)的面积最小,可得切点坐标,利用三角形的面积公式,建立方程,即可求出实数m的值.【解答】解:由题意,切线方程为=1,∵直线l与x、y轴分别相交于点A、B,∴A(,0),B(0,),∴S△AOB=,∵=1≥,∴≥,∴S△AOB≥ab,当且仅当==时,△AOB(O为坐标原点)的面积最小,设|PF1|=x,|PF2|=y,由余弦定理可得4c2=x2+y2﹣xy,∴xy=b2,∴==b2,∴=b2,∴x0==b,∴c=b,∴a= b∵∠F1PF2的内角平分线长度为a,∴×x×a×+×y×a×=b2,∴×(x+y)=b2,∴××2a=b2,∴m=.故选:A.二、填空题(共20分)13.已知x>y>0,则与中较大者是.【考点】不等式的证明.【分析】根据已知中x>y>0,利用作差法,可得与的大小关系,进而得到答案.【解答】解:∵x>y>0,∴x﹣y>0,y+1>0,﹣=>0,故与中较大者是,故答案为:14.△ABC中,角A、B、C所对的边分别为a、b、c,B=,sinA:sinC=4:3,且△ABC的面积为,则c=.【考点】正弦定理.【分析】由正弦定理和条件求出a:c的值,根据三角形的面积公式列出方程,联立方程后求出c的值.【解答】解:∵sinA:sinC=4:3,∴由正弦定理得,a:c=4:3,①∵B=,且△ABC的面积为,∴,解得ac=4,②由①②解得,c=,故答案为:.15.等边△ABC的边长为2,且,则=.【考点】平面向量数量积的运算.【分析】根据平面向量数量积的定义进行转化求解即可.【解答】解:∵,∴=,=,即D是BC的中点,则=(+)•(+)=(﹣+)•(+)= [﹣2+2+•﹣•]= [﹣4+×42+×2×2cos60°﹣2×2×cos60°]=(﹣4++﹣2)==,故答案为:16.已知圆C的圆心在直线x+y﹣2=0上,圆C经过点(2,﹣2)且被x轴截得的弦长为2,则圆C的标准方程为(x﹣3)2+(y+1)2=2或(x﹣5)2+(y+3)2=10.【考点】圆的标准方程.【分析】由题意,设圆心坐标为(a,2﹣a),则r2=(a﹣2)2+(2﹣a+22)=12+(2﹣a)2,求出a,r,可得圆心与半径,即可求出圆C的标准方程.【解答】解:由题意,设圆心坐标为(a,2﹣a),则r2=(a﹣2)2+(2﹣a+22)=12+(2﹣a)2,∴a=3,r=或a=5,r=,∴圆C的标准方程为(x﹣3)2+(y+1)2=2或(x﹣5)2+(y+3)2=10.故答案为:(x﹣3)2+(y+1)2=2或(x﹣5)2+(y+3)2=10.三、解答题(共70分)17.已知椭圆=1的左、右焦点分别为F1、F2,点P在该椭圆上.(1)求实数m的取值范围;(2)若m=5,且|PF1|=3,求点P到x轴的距离.【考点】椭圆的简单性质.【分析】(1)由题意,,即可求实数m的取值范围;(2)求出|PF2|=1,|F1F2|=2,可得|PF1|2=|PF2|2+|F1F2|2,即可求点P到x轴的距离.【解答】解:(1)由题意,,∴3<m<9且m≠6;(2)m=5,椭圆方程为=1,∴a=2,b=,c=∵|PF1|=3,∴|PF2|=1,∵|F1F2|=2,∴|PF1|2=|PF2|2+|F1F2|2,∴P到x轴的距离为1.18.△ABC中,角A、B、C所对的边分别为a、b、c,角A为锐角,且.(1)求角C的大小;(2)求sinA+sinB的取值范围.【考点】正弦定理.【分析】(1)根据二倍角的正弦公式、商的关系化简后,再由余弦定理化简后求出C的值;(2)由(1)和内角和定理表示B,利用诱导公式、两角和的正弦公式化简后,由角A为锐角和正弦函数的性质,求出sinA+sinB的取值范围.【解答】解:(1)由题意得,,∴,得,∵角A为锐角,∴cosA=,由余弦定理得,,化简得c2=a2+b2,∴C=;(2)由(1)得,A+B=,则B=﹣A,∴sinA+sinB=sinA+sin(﹣A)=sinA+cosA=,由得,,∴,则,∴sinA+sinB的取值范围是(1,].19.已知圆的方程为x2+y2﹣2x﹣2my+2m2﹣4m+1=0(m∈R).(1)当该圆的半径最长时,求m的值;(2)在满足(1)的条件下,若该圆的圆周上到直线l:2kx﹣2y+4+﹣3k=0的距离等于1的点有且只有3个,求实数k的值.【考点】直线与圆的位置关系;圆的一般方程.【分析】(1)圆的方程x2+y2﹣2x﹣2my+2m2﹣4m+1=0化为(x﹣1)2+(y﹣m)2=﹣m2+4m,当﹣m2+4m>0时表示圆,半径最大时,﹣m2+4m取得最大值,求出对应m的值;(2)圆周上到直线l的距离等于1的点有且只有3个时,圆心到直线l的距离d=r﹣1,列出方程求出k的值.【解答】解:(1)圆的方程x2+y2﹣2x﹣2my+2m2﹣4m+1=0可化为:(x﹣1)2+(y﹣m)2=﹣m2+4m,它表示圆时,应有﹣m2+4m>0,解得0<m<4;当半径最大时,应有﹣m2+4m最大,此时m=2,圆的方程为x2+y2﹣2x﹣4y+1=0;(2)圆的方程x2+y2﹣2x﹣4y+1=0,化为(x﹣1)2+(y﹣2)2=4;该圆的圆周上到直线l:2kx﹣2y+4+﹣3k=0的距离等于1的点有且只有3个,则圆心(1,2)到直线l的距离d等于半径r﹣1,即=1,化简得=4k2+4,解得k=﹣.20.已知S n是数列{a n}的前n项和,且a1=2,a n+1=3S n﹣2(n∈N*).(1)求数列{a n}的通项公式;(2)设b n=),求证,b1b2+b2b3+…+b n b n+1<3(n∈N*).【考点】数列与不等式的综合;数列递推式.【分析】(1)当n≥2时通过a n+1=3S n﹣2与a n=3S n﹣1﹣2作差,进而整理即得结论;(2)通过(1)可知数列{b n}的通项公式,利用裂项相消法计算即得结论.【解答】(1)解:∵a n+1=3S n﹣2,∴当n≥2时,a n=3S n﹣1﹣2,两式相减得:a n+1﹣a n=3a n,即a n+1=4a n(n≥2),又∵a1=2,a2=3S1﹣2=4,∴数列{a n}的通项公式a n=;(2)证明:由(1)可知b n=,∵当n≥2时,b n b n+1==﹣,∴b1b2+b2b3+…+b n b n+1=2×1+(1﹣)+(﹣)+…+(﹣)=3﹣<3.21.已知椭圆C:=1(a>b>0)的离心率为,且点(2,)在C上.(1)求C的方程;(2)过点P(2,1)的直线l与椭圆C交于A,B两点,且AB的中点恰为P,求直线l的方程.【考点】椭圆的简单性质.【分析】(1)根据椭圆C:=1(a>b>0)的离心率为,且点(2,)在C上,建立方程,可a2=16,b2=8,即可求出C的方程;(2)设A(x1,y1),B(x2,y2),则x1+x2=4,y1+y2=2,利用点差法求出直线的向量,可求直线l的方程.【解答】解:(1)∵椭圆C:=1(a>b>0)的离心率为,且点(2,)在C上,∴=,=1∴a2=16,b2=8,∴C的方程为=1;(2)设A(x1,y1),B(x2,y2),则x1+x2=4,y1+y2=2;由(1)知,8x12+16y12=128,①8x22+16y22=128,②①﹣②得:8(x1+x2)(x1﹣x2)+16(y1+y2)(y2﹣y1)=0,∴32(x1﹣x2)+32(y2﹣y1)=0,由题意知,直线l的斜率存在,k=﹣1,∴直线l的方程为y﹣1=﹣(x﹣2),即x+y﹣3=0.22.已知椭圆C:=1(a>b>0)的两焦点F1、F2与短轴两端点构成四边形为正方形,又点M是C上任意一点,且△MF1F2的周长为2+2.(1)求椭圆C的方程;(2)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆E上一点,且满足(O为坐标原点),当|AB|<时,求实数t的取值范围.【考点】椭圆的简单性质.【分析】(1)运用椭圆的定义和范围,可得2a+2c=2+2,b=c,a2﹣b2=c2,解方程可得a,b,即可得到椭圆方程;(2)由题意知直AB的斜率存在.AB:y=k(x﹣2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得k值取值范围,再结合向量的坐标运算利用点P在椭圆上,建立k与t的关系式,利用函数的单调性求出实数t取值范围,从而解决问题.【解答】解:(1)△MF1F2的周长是2+2,即为|MF1|+|MF2|+|F1F2|=2a+2c=2+2,由椭圆C:=1(a>b>0)的两焦点F1、F2与短轴两端点构成四边形为正方形,即有b=c,a2﹣b2=c2,解得a=,b=1,则椭圆的方程为y2=1;(2)由题意知直AB的斜率存在.AB:y=k(x﹣2),设A(x1,y1),B(x2,y2),P(x,y)代入椭圆方程,得(1+2k2)x2﹣8k2x+8k2﹣2=0,△=64k4﹣4(2k2+1)(8k2﹣2)>0,k2<∴x1x2=,x1+x2=,∵|AB|<,∴|x1﹣x2|<,∴(1+k2)[()2﹣4×]<,∴(4k2﹣1)(14k2+13)>0,∴k2>,∴<k2<,∵满足,∴(x1+x2,y1+y2)=t(x,y),∴x==•,y=•(y1+y2)=,∵点P在椭圆上,∴(•)2+2()2=2∴16k2=t2(1+2k2)∴t2==8﹣,由于<k2<,∴﹣2<t<﹣或<t<2∴实数t取值范围为:﹣2<t<﹣或<t<2.2016年8月27日。
重庆市巴蜀中学2015-2016学年高一10月月考数学试题一、选择题(本题10个小题,每小题5分,共50分)1、已知集合A ={4,5,7,9},B ={3,4,7,8,9},全集U =A∪B,则集合C U (A∩B)=( )A 、{}4,7,9B 、{}5,7,9C 、{}3,5,8D 、{}7,8,92、已知函数f (x )满足f (x -1)=x 2,则f (x )的解析式为( )A 、2()(1)f x x =+B 、2()(1)f x x =-C 、2()1f x x =+D 、2()1f x x =-3、下列四个函数中,与函数y =x 是同一个函数的是( )A 、2x y x= B 、2y = C 、y = D 、y = 4、“x =0”是“x ﹥0”的( )A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件5、设集合A ={x |1≤x ≤2},B ={y |1≤y ≤4},则下述对应法则f 中,不能构成A 到B 的映射的是( )A 、f :2x y x →=B 、:32f x y x →=-C 、:4f x y x →=-+D 、2:4f x y x →=-6、下列函数中,在(-∞,0)上为增函数的是( )A 、y =、1x y x=- C 、2(1)y x =-+ D 、21y x =+ 7、对任意的实数x ,y ,函数f (x )都满足f (x +y )=f (x )+f (y )+2恒成立。
则f (2)+f (-2)=( )A 、-4B 、0C 、-2D 、28、设f (x )是(-∞,+∞)上的减函数,则不等式f (2)﹤1()f x 的解集是( )A 、1(0,)2B 、1(,)2-∞C 、1(,)2+∞D 、1(,0)(,)2-∞+∞9、设集合A={x|101x x -+≤},B ={x ||x -b|≤a},若“a =1”是“A∩B≠Ф”的充分条件,则b 的取值范围是( )A 、(-2,2)B 、(]2,2-C 、[)2,2-D 、[]2,2-10、定义在[1,+∞)上的函数f (x )满足:(1)f (2x )=2f (x );(2)当2≤x ≤4时, f (x )=1-|x -3|,则集合A ={x |f (x )=f (61)}中的最小元素是( )A 、13B 、11C 、9D 、6二、填空题(本题5个小题,每个5分,共25分)11、满足条件{1,2}∪A={1,2,3,4,5}的集合A 的个数为 。
2015-2016学年重庆市渝中区巴蜀中学高一(下)期末语文试卷一、现代文阅读.(9分,每小题9分)1.阅读下面的文字,完成下列各题。
英国脱离欧盟,被认为将重创全球经济和英国自身经济前景,很多国际政要、经济组织、知名企业负责人此前就在纷纷指出这方面的危害性。
经合组织(OECD)在最新发布的《全球经济展望》中,警告英国脱欧将让美国、riben、金砖国家等经济体不同程度地受到冲击,并且在2016~2018年,英国每年国内生产总值也将损失0.5%,到2020年,英国的GDP比未退欧情景下还要低3%.中信里昂(一家金融机构)报告称,英国脱欧将令英镑大幅贬值,并减慢经济增长及推高通胀,意味英国出现经济衰退的机会将大增。
普华永道也曾分析英国脱欧的代价,估计至2020年,英国国内生产总值(GDP)将萎缩约100亿英镑,相当于其GDP的5%,英国的金融业也将损失近10万个工作岗位。
同时,美联储政策制定者将退欧公投视为是否在今年夏天加息的一个因素。
美联储主席耶伦早些时候表示,公投退出欧盟将对经济产生“显著影响”。
据《华尔街日报》报道,目前,全球主要央行已经在探讨若英国公投支持退出欧盟,应该如何应对这一决定可能引发的金融动荡,例如美元流动性急剧收紧等。
一些参与讨论的官员担心,英国脱欧可能会引发类似于2008年全球金融危机爆发之初出现的美元严重短缺局面。
自2008年金融海啸后,全球一些最大央行自那时起已经建立了一个体系,使其能够在必要时从美联储借入美元,但其中一位央行官员称,如果英国脱欧公投在金融市场引发足够大的冲击波,仅靠该体系并不能保障为全球经济提供足够的美元供应。
该人士指出,能够获得美元供应的机构有限,关键问题是这些美元能否到达这些机构之外,流入更广泛的经济领域。
该人士又称,美联储之外的各国央行也注意到美国国会对这项美元借贷计划所持的强硬立场。
更值得警惕的是,受欧洲经济持续低迷、难民问题、恐怖袭击频发等多个因素的影响,“脱欧”情绪正在欧洲地区蔓延。