北京市朝阳区2016届高三上学期期中考试数学文试卷

北京市朝阳区2015—2016学年度高三年级第一学期期末统一考试数学试卷（文史类） 2016.1(考试时间120分钟 满分150分）本试卷分为选择题(共40分）和非选择题（共110分）两部分第一部分(选择题 共40分）一、选择题:本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项。

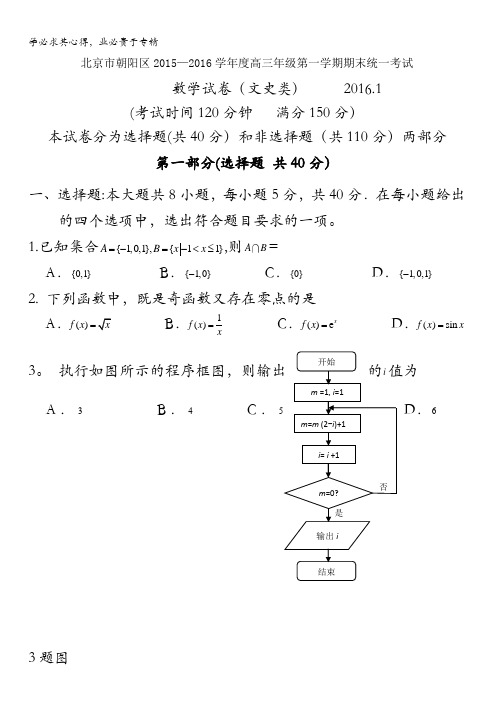
1.已知集合{1,0,1},{11}A B x x =-=-<≤,则AB =A ．{0,1}B ．{1,0}-C ．{0}D ．{1,0,1}- 2. 下列函数中，既是奇函数又存在零点的是A ．()f x =B ．1()f x x= C ．()e xf x = D ．()sin f x x =3。

A ．3B ．4C ．D ．63题图km/h ）频率4．在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计，统计结果如下面的频率分布直方图所示．若该处高速公路规定正常行驶速度为90km/h~120km/h ，试估计2000辆车中，在这段时间内以正常速度通过该处的汽车约有A ．30辆 B ．300辆 C ．170辆 D ．1700辆4 第 4题图5. 已知m ，n 表示两条不同的直线，αβ，表示两个不同的平面，且m n αβ⊂⊂，，则下列说法正确的是A ．若//αβ，则//m nB ．若m β⊥，则αβ⊥C ．若//m β，则//αβD ．若αβ⊥，则m n ⊥ 6。

设斜率为2的直线l 过抛物线2(0)yax a =≠的焦点F ，且与y 轴交于点A，若OAF ∆（O 为坐标原点）的面积为4,则抛物线方程为A 。

24yx=± B 。

24y x= C.28y x=± D.28y x =7。

已知B A ,为圆9)()(:22=-+-n y m x C （,m n ∈R ）上两个不同的点（C 为圆心）,且满足13||=+CB CA ,则=ABA. 23 B 。

北京市朝阳区高三年级第一次综合练习数学试卷（文史类） 2016.3 （考试时间120分钟分钟 满分150分）分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项要求的一项. .1. 已知全集U =R ，集合{}3A x x =£，{}2B x x =<，则()U BA = ð A ．{}2x x £B ．{}13x x ££ C. {}23x x <£ D ．{}23x x ££ 2.已知i 为虚数单位为虚数单位,,则复数2i1i+= A ．1i + B ．1i - C ．1i -+ D ．1i -- 3.已知非零平面向量,a b ，“+=-a b a b ”是“^a b ”的”的 A ．充分而不必要条件．充分而不必要条件 B ．必要而不充分条件．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件4.执行如图所示的程序框图，输出的S 值为值为 A. 42 B. 19 C. 8 D. 35.在ABC D 中，角,,A B C 所对的边分别为,,a b c ，若3cos sin 0a B b A +=，则B = A. π6B. π3 C. 2π3D. 5π6i =1,S =1 i <4? S = 2S+i i = i+1 开始开始 输出S 结束结束否是6.已知某四棱锥的三视图如图所示，则该四棱锥的侧面积是已知某四棱锥的三视图如图所示，则该四棱锥的侧面积是A. 33+B. 3+6C. 123+D.126+7. 某工厂一年中各月份的收入、支出情况的统计如图所示某工厂一年中各月份的收入、支出情况的统计如图所示,,下列说法中错误．．的是的是 A. 收入最高值与收入最低值的比是3:1B. 结余最高的月份是7月份月份C.1至2月份的收入的变化率与4至5月份的收入的变化率相同月份的收入的变化率相同D. 前6个月的平均收入为40万元万元 （注：结余（注：结余==收入收入--支出）支出）8. 若圆222(1)x y r +-=与曲线(1)1x y -=的没有公共点，则半径r 的取值范围是的取值范围是 A ．02r << B ．1102r <<C ．03r <<D ．1302r <<万元万元 月O 23 4 30 1 10 20 5 6 89 10 71112 40 60 50 70 90 80 收入收入 支出支出1 3 2正视图正视图俯视图俯视图 侧视图侧视图1 1 第二部分（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分把答案填在答题卡上. 9.已知函数22log (3),0,(), 0,x x f x x x +³ì=í<î则((1))f f -= . 10.已知双曲线221x y m-=过抛物线28y x =的焦点，则此双曲线的渐近线方程为的焦点，则此双曲线的渐近线方程为. 11.已知递增的等差数列}{n a ()n *ÎN 的首项11=a ，且1a ,2a ,4a 成等比数列，则数列}{n a 的通项公式n a = ；48124+4+n a a a a +++ =____. 12.已知不等式组0,,290y y x x y ³ìï£íï+-£î表示的平面区域为D .若直线()1y a x =+与区域D 有公共点，则实数a 的取值范围是的取值范围是 . 13.已知圆22:(3)(5)5C x y -+-=，过圆心C 的直线l 交圆C 于,A B 两点，交y 轴于点P . 若A 恰为PB 的中点，则直线l 的方程为的方程为 . 14.甲乙两人做游戏，游戏的规则是：两人轮流从1（1必须报）开始连续报数，每人一次最少要报一个数，最多可以连续报7个数（如，一个人先报数“1，2”，则下一个人可以有“3”， “3，4”，…，“3，4，5，6，7，8，9”等七种报数方法），谁抢先报到“100”则谁获胜.如果从甲开始，则甲要想必胜，第一次报的数应该是要想必胜，第一次报的数应该是 . 三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15.（本小题满分13分）分）已知函数()2sin cos()3f x x x w w p =+（0w >）的最小正周期为p . （Ⅰ）求w 的值；的值；（Ⅱ）求()f x 在区间[,]62p p-上的最大值和最小值. 16.(本小题满分13分）分）已知数列已知数列{}n a 的前n 项和22n S n n =-,n *ÎN . （Ⅰ）求数列{}n a 的通项公式；的通项公式；（Ⅱ）若()1nn n b a =-，求数列{}n b 的前n 项和n T . 17. (本小题满分本小题满分13分) 某班倡议假期每位学生至少阅读一本名著，为了解学生的阅读情况，对该班所有学生进行了调查.调查结果如下表: （Ⅰ）试根据上述数据，求这个班级女生阅读（Ⅰ）试根据上述数据，求这个班级女生阅读名著名著的平均本数; （Ⅱ）若从阅读5本名著的学生中任选2人交流读书心得，求选到男生和女生各1人的概率人的概率；； （Ⅲ）试判断该班男生阅读名著本数的方差21s 与女生阅读名著本数的方差22s 的大小的大小（只需写出结论）．（注：方差2222121[()()()]n s x x x x x x n=-+-++- ，其中x 为1x 2x ，…… n x 的平均数）的平均数） 18.（本小题共14分）分）如图，在三棱柱111ABC A B C -中，1AA ^底面ABC ，90BAC Ð=°，2AB AC ==，13AA =．,M N 分别为BC 和1CC 的中点，P 为侧棱1BB 上的动点．上的动点．（Ⅰ）求证：平面APM ^平面11BBC C ；（Ⅱ）若P 为线段1BB 的中点，求证：1//A N 平面APM ； （Ⅲ）试判断直线1BC 与平面APM 是否能够垂直. 若能垂直，求PB 的值；若不能垂直，请说明理由．的值；若不能垂直，请说明理由．19.(本小题共14分）分）已知椭圆已知椭圆:C 22142x y +=的焦点分别为12,F F .（Ⅰ）求以线段12F F 为直径的圆的方程；为直径的圆的方程；（Ⅱ）过点(4,0)P 任作一条直线l 与椭圆C 交于不同的两点,M N .在x 轴上是否存在点Q ，使得180PQM PQN Ð+Ð=°？若存在，求出点Q 的坐标；若不存在，请说明理由的坐标；若不存在，请说明理由..20. （本题满分13分）分）阅读名著的本数 1 2 3 4 5 男生人数 3 1 2 1 3 女生人数1 3 3 1 2 NAMPCBA 1 C 1 B 1 已知函数()e x k x f x k x+=×-()k ÎR. （Ⅰ）若1,k =求曲线()y f x =在点()0(0)f ，处的切线方程；处的切线方程； （Ⅱ）求函数()f x 的单调区间；的单调区间； （Ⅲ）设0k £，若函数()f x 在区间()3,22上存在极值点，求k 的取值范围的取值范围. .北京市朝阳区高三年级第一次综合练习数学答案（文史类） 2016.3 一、选择题：（满分40分） 题号题号 1 2 3 4 5 6 7 8 答案答案D A C B C B D C 二、填空题：（满分30分） 题号题号9 10 11 12 13 14 答案答案212y x =±n a n=，2264n n ++3[0,]4210x y --=或2110x y +-=1，2，3，4 （注：两空的填空，第一空3分，第二空2分） 三、解答题：（满分80分） 15. （本小题满分13分）分）解：（Ⅰ）()2sin cos()3f x x x w w p =+132sin (cos sin )22x x x w w w =- 2sin cos 3sin x x x w w w =-133sin 2cos2222x x w w =+- 3sin(2)32x w p=+-. 因为()f x 的最小正周期为2T w2p==p ，则1w =. …………………6分（Ⅱ）由（Ⅰ）可知3()sin(2)32f x x p=+-. 因为,6x p p -££2所以0233x p 4p £+£. 则3sin(2)123x p-£+£. 当232x pp +=，即12x p=时，()f x 取得最大值是312-； 当233x p4p+=，即2x p=时，()f x 取得最小值是3-. ()f x 在区间[,]62p p-的最大值为312-，最小值为3-. …………………13分16. （本小题满分13分）分） 解：（Ⅰ）由22n S n n =-，当2n ³时，()()221=22114 3.-éù=------=-ëûnnn a S S n n n n n当1n =时，111,a S ==而4131´-=，所以数列{}n a的通项公式43n a n =-，n *ÎN . ………………………6分（Ⅱ）由（Ⅰ）可得()(1)(1)43,=-=--n nn n b a n当n 为偶数时，()159********,2nnT n n =-+-+-++-=´=当n 为奇数时，1n +为偶数，112(1)(41)2 1.n n n T T b n n n ++=-=+-+=-+综上，2,,21,.n n n T n n ì=í-+î为偶数为奇数 …………………………13分17.（本小题满分13分）分）解：（Ⅰ）女生阅读（Ⅰ）女生阅读名著名著的平均本数11323314+25310x ´+´+´+´´==本. …………………………3分（Ⅱ）设事件A ={={从阅读从阅读5本名著的学生中任取2人，其中男生和女生各1人}.}.男生阅读5本名著的3人分别记为123,,a a a ，女生阅读5本名著的2人分别记为12,.b b从阅读5本名著的5名学生中任取2人，共有10个结果，分别是：个结果，分别是： {}12,a a ，{}13,a a ，{}23,a a ，{}12,b b ，{}11,a b ，{}12,a b ，{}21,a b ，{}22,a b ，{}31,a b ，{}32,a b . 其中男生和女生各1人共有6个结果，分别是：个结果，分别是：{}11,a b ，{}12,a b ，{}21,a b ，{}22,a b ，{}31,a b ，{}32,a b . 则63105P A ==（）. …………………………10分（III ）2212s s >. …………………………13分18. （本小题满分14分）分） 证明：证明：（Ⅰ）由已知，M 为BC 中点，且AB AC =，所以AM BC ^．又因为11//BB AA ，且1AA ^底面ABC ，所以1BB ^底面ABC ． 因为AM Ì底面ABC ，所以1BB AM ^， 又1BB BC B = ， 所以AM ^平面11BBC C．又因为AM Ì平面APM ，所以平面APM ^平面11BBC C ． ……………………5分（Ⅱ）（Ⅱ）取11C B 中点D ，连结1A D ，DN ，DM ，1B C . 由于D ，M 分别为11C B ，CB 的中点，的中点， 所以DM //1A A ,且DM =1A A . 则四边形1A AMD 为平行四边形，所以1A D //AM . 又1A D Ë平面APM ，AM Ì平面APM ， 所以1A D //平面APM . 由于D ，N 分别为11C B ，1C C 的中点，的中点，NAMPCB A 1 C 1 B 1 D所以DN //1B C . 又P ，M 分别为1B B ，CB 的中点，的中点， 所以MP //1B C . 则DN //MP . 又DN Ë平面APM ，MP Ì平面APM ， 所以DN //平面APM . 由于1A D =DN D ,所以平面1A DN //平面APM . 由于1A N Ì平面1A DN ，所以1//A N 平面APM . ……………10分（III ）假设1BC 与平面APM 垂直，垂直， 由PM Ì平面APM ，则1BC PM ^． 设PB x =，[0,3]x Î．当1BC PM ^时，11BPMB C B Ð=Ð，所以Rt PBM D ∽11Rt B C B DÐ，所以111C B PB MB BB =． 由已知1112,22,3MB C B BB ===， 所以2223x =，得433x =．由于43[0,3]3x =Ï， 因此直线1BC 与平面APM 不能垂直．不能垂直． …………………………………………14分19. （本小题满分13分）分） 解：（I ）因为24a =，22b =，所以22c =.所以以线段12F F 为直径的圆的方程为222x y +=.……………………………3分（II ）若存在点(,0)Q m ，使得180PQM PQN Ð+Ð=°，则直线则直线QM 和QN 的斜率存在的斜率存在,,分别设为1k ,2k . 等价于等价于120k k +=.依题意，直线l 的斜率存在，故设直线l 的方程为(4)y k x =-.由22(4)142y k x x y =-ìïí+=ïî，得2222(21)163240k x k x k +-+-=.因为直线l 与椭圆C 有两个交点，所以0D >. 即2222(16)4(21)(324)0k k k -+->，解得216k <. 设11(,)M x y ，22(,)N x y ,则21221621k x x k +=+，212232421k x x k -=+， 11(4)y k x =-，22(4)y k x =-.令1212120y y k k x mx m+=+=--，1221()()0,x m y x m y -+-=1221()(4)()(4)0x m k x x m k x --+--=,当0k ¹时，12122(4)()80x x m x x m -+++=，所以22324221k k -´+2216(4)8021k m m k -+´+=+， 化简得，28(1)021m k -=+，所以1m =.当0k =时，也成立时，也成立. .所以存在点(1,0)Q ，使得180PQM PQN Ð+Ð=°.……………………………14分20. （本小题满分13分）分）解：(Ⅰ)若1k =，函数()f x 的定义域为{}1x x ¹，22e (3)()=1)xx f x x -¢-（.则曲线()y f x =在点()0(0)f ，处切线的斜率为(0)=3f ¢. 而(0)=1f ，则曲线()y f x =在点()0(0)f ，处切线的方程为31y x =+. …………………………3分BA O yxQ NMP (4,0)（Ⅱ）函数()f x 的定义域为{}x x k ¹，222e (2)()=)x k k x f x k x +-¢-（.（1）当0k >时，由x k ¹,且此时22k k k +>，可得2222k k k k k -+<<+.令()0f x ¢<，解得22x k k <+-或22x k k >+，函数()f x 为减函数；为减函数；令()0f x ¢>，解得2222k k x k k -+<<+，但x k ¹，所以当22k k x k -+<<，22k x k k <<+时，函数()f x 也为增函数. 所以函数()f x 的单调减区间为22)k k ¥+（-，-，22+)k k +¥（，， 单调增区间为22)k k k +（-，，2,2)k k k +（.（2）当0k =时，函数()f x 的单调减区间为¥（-,0)，+¥（0,). 当2k =-时，函数()f x 的单调减区间为2¥（-,-)，2+¥（-，). 当20k -<<时，由220k k +<，所以函数()f x 的单调减区间为k ¥（-,)，+k ¥（,). 即当20k -££时，函数()f x 的单调减区间为k ¥（-,)，+k ¥（,). （3）当2k <-时，此时22k k k +>-. 令()0f x ¢<，解得22x k k <+-或22x k k >+，但x k ¹，所以当x k <，22k x k k <<+-，22x k k >+时，函数()f x 为减函数；为减函数；令()0f x ¢>，解得2222k k x k k -+<<+，函数()f x 为增函数. 所以函数()f x 的单调减区间为k ¥（-,)，22k k k +（,-)，22,)k k ++¥（， 函数()f x 的单调增区间为222,2)k k k k ++（-. . ……………………9分（Ⅲ）（1）当20k -££时，由（Ⅱ）问可知，函数()f x 在(3,22)上为减函数，所以不存在极值点; （2）当2k <-时，由（Ⅱ）可知，()f x 在222,2)k k k k ++（-上为增函数，上为增函数，在在22,)k k ++¥（上为减函数上为减函数.. 若函数()f x 在区间(3,22)上存在极值点，则23222k k <+<， 解得43k -<<-或12k <<,所以43k -<<-.综上所述，当综上所述，当43k -<<-时，函数()f x 在区间()3,22上存在极值点上存在极值点. .……………………13分。

（考试时间120分钟 满分150分）本试卷分为选择题(共40分)和非选择题(共110分）两部分第一部分（选择题 共40分)一、选择题:本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中,选出符合题目要求的一项.1。

已知集合}2{>=x x A ,B ＝{(1)(3)0}x x x --<，则A ∩B =（ ）A ．{1}x x >B ．{23}x x <<C ．{13}x x <<D ．{2x x >或1}x < 【答案】B考点：集合间的运算。

2. 设平面向量(,1)x =a ，(4,)x =b ， 且⋅a b 1=-， 则实数x 的值是（ )A ．2-B ．1-C ．13- D ．15-【答案】D 【解析】试题分析：(,1)a x =，(4,)b x = 所以451a b x x x =+==-，解得15x =-故答案选D考点：向量的数量积。

3。

下列函数在(,0)(0,)-∞+∞上既是偶函数,又在),0(+∞上单调递增的是（ ）A ．2y x =- B ．1y x -= C．2log y x =D ．2xy =-【答案】C 【解析】试题分析：易判断A 、C 选项函数的偶函数，A 选项2y x =-是开口向下二次函数，其在(0,)+∞单调递减，C 选项2log ||y x =,当0x >时，2log y x =,由对数函数性质知，其在(0,)+∞单调递增故答案选C考点：函数的奇偶性和单调性.4．已知1tan 3θ=，那么πtan ()4θ+等于 （ ) A ．2 B ．2- C ．12D ．12-【答案】A 【解析】试题分析：11tan tan34tan()2141tan tan 1143πθπθπθ+++===--⨯ 故答案选A考点：正切函数的和差公式。

5。

要得到函数sin(2)3y x π=-的图象，只需将函数sin 2y x =的图象( )A ．向左平移π6个单位 B ．向右平移π6个单位C ．向左平移π3个单位D ．向右平移π3个单位【答案】B考点:三角函数的图像平移.6。

北京市朝阳区 2016 届高三上学期期中考试数学试卷（文科）（考试时间120 分钟满分150 分）本试卷分为选择题（共40 分）和非选择题（共110 分）两部分第一部分（选择题共40 分）一、选择题：本大题共8 小题，每小题 5 分，共 40 分．在每小题给出的四个选项中，选出符合题目要求的一项 .1. 已知集合A{ x x2} ，B＝{ x (x1)(x3)0} ，则A∩B=（）A ． { x x 1}B．{ x 2 x 3}C．{ x 1 x 3}D． { x x 2 或x 1}2. 设平面向量a( x,1) ，b (4, x) , 且a b1,则实数x的值是（）A ．2B ．111 C． D ．353.下列函数在(,0)(0, ) 上既是偶函数，又在(0, ) 上单调递增的是（）A ．y x2B ．y x 1C．y log 2 x D． y2x4．已知tan 1，那么 tan(π3) 等于（）4A ．2B．2C．1D．1 225.要得到函数y sin(2 x) 的图象，只需将函数y sin 2x 的图象（）3A ．向左平移个单位B．向右平移个单位66 C．向左平移个单位D．向右平移个单位336.下列命题正确的是（）A.“x 1”是“x23x 2 0 ”的必要不充分条件1C. 若 p q 为假命题，则 p, q 均为假命题D. 命题 “若 x 23x 20 ，则 x2 ”的否命题为 “若 x 2 3x 20, 则 x 27.在 ABC 中，已知 AB AC4 ， BC3 ， M , N 分别是 BC 边上的三等分点，则AM AN的值是（）21 C ． 6D ． 8A ． 5B ．48. 已知函数 f (x)x 2, 0 x a,若存在实数 b ，使函数 g(x)f ( x) b 有两个零点，2x ,xa.则实数 a 的取值范围是（）A ． (0, 2)B ． (2, )C ． (2, 4)D ． (4, )第二部分（非选择题共110 分）二、填空题：本大题共6 小题，每小题 5 分，共 30 分 .把答案填在答题卡上 .1 9.若集合 { a,0,1} ={ c, , 1} ，则 a _____,b_______.b10.设等差数列a n 的前 n 项和为 S n ，若 a 3 a 6 12 ， S 4 8 ，则 a 9 的值是．11.给出四个命题：①平行于同一平面的两个不重合的平面平行；②平行于同一直线的两个不重合的平面平行；③垂直于同一平面的两个不重合的平面平行；④垂直于同一直线的两个不重合的平面平行；其中真命题的序号是 ________．12．已知函数 f (x) 2sinx (0 )的最小正周期为，则，在 0,( ) 内满足 f ( x 0 ) 0的 x 0＝．π π13. 若函数 f (x) a sin xcosx 在区间 ( ,) 上单调递增，则实数 a 的取值范围是 .6 414. 如 图 ， 在 ABC 中 ， A B A C 4 ，BAC 90 ， D 是 BC 的 中 点 ， 若 向 量AM1AB mAC （ m R ），且点 M 在 ACD 的内部（不含边界） ，则 AM BM 的取值范4围是．三、解答题：本大题共 6 小题，共80 分 .解答应写出文字说明，演算步骤或证明过程.15. （本小题满分13 分）已知函数 f ( x) 2 3sin xcosx2cos 2x. 222（Ⅰ）求 f ( x) 的最小正周期；（Ⅱ）求 f ( x) 的单调递减区间.16.（本小题满分 13 分）设等差数列a n的前n项和为 S n，n N ，公差d0, S315, 已知a1, a4, a13成等比数列 .（Ⅰ）求数列a n的通项公式；（Ⅱ）设 b n a2n，求数列b n的前n项和T n.17.（本小题满分14 分）如图 , 在三棱柱ABC A1B1C1中，CC1底面ABC ,AC CB ,点 D 是 AB 的中点．（Ⅰ）求证：AC BC1；（Ⅱ）求证：AC1∥平面 CDB1.(Ⅲ )设AB2AA1, AC BC ,在线段A1 B1上是否存在点M ，使得 BM CB1?若存在,确定点 M 的位置;若不存在，说明理由.18.（本小题满分 13 分）在 ABC 中，角A,B,C所对的边分别为a,b,c．已知 cos B 1 ．2（Ⅰ）若 a 2, b 2 3 ，求 ABC 的面积；（Ⅱ）求 sin A sin C 的取值范围．19. （本小题满分13 分）已知函数 f ( x) a ln x x2( a 1) x ，a R．2（Ⅰ）若函数 f ( x) 在区间 (1,3) 上单调递减，求 a 的取值范围；（Ⅱ）当 a 1 时，证明1 f ( x).220.（本小题满分 14 分）已知函数 f ( x) e x (ax2bx 1) (其中 a ，b R ),函数f ( x)的导函数为f ( x)，且f ( 1)0．(Ⅰ )若b 1 ，求曲线 y f (x) 在点 (0, f (0)) 处的切线方程；(Ⅱ )若函数 f (x) 在区间 [ 1,1] 上的最小值为0 ，求 b 的值．参考答案一、：（分 40分）号12345678答案B D C A B B C C 二、填空：（分 30分）号91011121314答案1,115①④ 2 ,[1, )2,62（注：两空的填空，第一空 3 分，第二空 2 分）三、解答：（分 80 分）15.（本小分 13 分）（I ）由已知可得：f ( x)3sin x cosx 12sin( x)1 .6所以 f (x) 的最小正周期 2 .⋯⋯⋯⋯⋯⋯⋯ ..7 分（II ）由2k x2k， k Z ,22得 2k x2k, k Z .33因此函数 f (x) 的减区 [2 k,2 k] , k Z.33⋯⋯⋯⋯⋯⋯⋯..13分16.（本小分 13 分）解：（ I）依意，3a32 d15,12( a13d)2a1 ( a1 12d ).a13,解得d2.因此 a n a1( n 1)d 3 2(n 1) 2n 1, 即a n2n 1 .⋯⋯⋯⋯⋯⋯⋯..6分(Ⅱ )依意，b n a2n22n12n 11.T n b1 b2b n(221)(231)(2n 1 1)=2223...2n1n4(1 2 n )n122n2n 4.⋯⋯⋯⋯⋯⋯⋯ ..13分17.（本小分14 分）（ I）在三棱柱ABC A1 B1 C1中，因 CC1底面ABC，AC底面ABC，所以 CC1AC .又 AC BC ，BC CC1 C ,所以 AC平面BCC1B1．而BC1平面BCC1B1，AC BC1.⋯⋯⋯⋯⋯⋯⋯..4分(Ⅱ )CB1与 C1 B 的交点E，DE，因 D 是 AB 的中点， E 是BC1的中点，E 所以 DE ∥AC1.因 DE平面CDB1，AC1平面CDB1，所以AC1∥平面CDB1.⋯⋯⋯⋯⋯⋯⋯ ..9分(Ⅲ )在段A1B1上存在点M，使得BM CB1,且M段A1B1的中点 .明如下：因 AA1底面 ABC ， CD底面 ABC ,M 所以 AA1CD .E 由已知 AC BC ，D段AB的中点，所以 CD AB .又 AA 1 AB A ，所以 CD 平面 AAB B .1 1取 段 A 1 B 1 的中点 M ， 接 BM . 因 BM 平面 AA 1B 1 B ，所以 CD BM .由已知 AB 2AA 1 ，由平面几何知 可得 BM B 1 D .又 CD B 1D D ,所以 BM 平面 B 1CD .又 11BC平面 B CD ，所以 BMCB 1 .⋯⋯⋯⋯⋯⋯⋯..14分18. （本小 分 13 分）（I ）在ABC 中，因 cos B1 ，2所以 B2π， sin B3 .32由正弦定理ab ,sin A sin B可得2 2 31 sin A, sin A.322又 A 角， A，所以 C .66所以 S ABC1ab sin C211 22 3223 .. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分（II ） sin A sinCsin( C) sinC3= sin C3cosC 1 ( sin C)22=3sin 2C1(1 cos2C )441sin(2C) 1 .264因 C(0,) ，3所以2C5( ,) .666 sin(2C)( 1 ,1].62所以 sin A sin C 的取范是1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯13分(0, ] .419.（本小分 13 分）解：（ I）函数的定域(0,) .因 f ( x)a(ax2(a 1)x a( x1)( x a) x1)x x. x又因函数 f ( x) 在(1,3)减，所以不等式( x1)(x a)0 在(1,3)上成立.g( x) ( x1)(x a) ， g (3)0 ，即 93(a1)a0 即可，解得 a 3.所以a的取范是[3,) .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分（Ⅱ）当 a 1 ， f ( x)ln x x2，2f (x)1xx21(x1)(x 1) x x x.令 f(x)0 ，得x1或 x 1 （舍）.当 x 化， f ( x), f ( x) 化情况如下表：x(0,1)1(1, )f ( x)0+f (x)极小所以 x 1,函数f ( x)的最小f (1)1 . 2所以 f (x)1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯13分成立 .220.（本小分 14 分）解：因 f (x)e x (ax2bx1) ，所以f( x)e x[ ax2(2a b) x b 1] ．因 f(1)0 ，所以 a(2 a b)b10 ．所以 a 1 ．⋯⋯⋯⋯⋯⋯⋯⋯2 分( Ⅰ)当a1， b1，f (0)1, f (0) 2 ，所以曲 y f (x) 在点(0, f (0)) 的切方程y12( x0) ．即 2x y 10．⋯⋯⋯⋯⋯⋯⋯⋯4 分(Ⅱ )由已知得f ( x)e x (x2bx 1)，所以f ( x) e x[ x2(2b) x b 1]e x ( x 1)(x b1)．（ 1）当b11，即 b0，令 f(x) e x (x1)(x b1) 0 得，x 1 或 x b1 ；(x1)(1)0 得，．令) e (f x x x b b 1 x1所以函数 f (x) 在 (1,) 和 (,b1)上增，在( b1, 1) 上减．所以函数 f (x) 在区 [1,1] 上增．所以函数 f ( x) 在区 [1,1] 上的最小 f ( 1) e 1 (2b)0 ．解得 b 2 ．然合意．（ 2）当b11，即 b0 ，f ( x)e x( x1)20 恒成立，所以函数 f ( x) 在 (,) 上增．所以函数 f (x) 在区 [ 1,1] 上增．所以函数 f ( x) 在区 [ 1,1]上的最小 f (1) e 1 (2b) 0 ．解得 b 2 ．然不符合意．（ 3）当b11，即 b0 ，令 f ( x) e x ( x1)(x b1) 0 得，x1或 x b 1 ；x1)(1) 0得，．令( ) e (f x x x b1x b 1所以函数 f (x) 在 (, 1) 和 ( b 1,) 上增，在 (1, b1) 上减．①若 b 11，即 b 2 ，函数 f ( x) 在区 [ 1,1] 上减．所以函数 f (x) 在区 [ 1,1] 上的最小 f (1)e(2b)0 ．解得 b 2 ．然合意．②若 b 11，即 2b0 ，函数 f ( x) 在在 (1,b1) 上减，在( b 1,1) 上增．此，函数 f ( x) 在区 [1,1] 上的最小 f ( b1) e b 1(b2)0 ．解得 b 2 ．然不合意．上所述， b 2 或b 2 所求．⋯⋯⋯⋯⋯⋯⋯⋯14分。

北京市朝阳区2016届高三上学期期中统一考试数学（文）试题（考试时间120分钟 满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.1. 已知集合}2{>=x x A ，B ＝{(1)(3)0}x x x --<，则A ∩B =A ．{1}x x >B ．{23}x x <<C ．{13}x x <<D ．{2x x >或1}x < 2. 设平面向量(,1)x =a ，(4,)x =b , 且⋅a b 1=-, 则实数x 的值是 A ．2- B ．1- C ．13-D ．15- 3.下列函数在(,0)(0,)-∞+∞上既是偶函数，又在),0(+∞上单调递增的是A ．2y x =- B ．1y x -= C ．2log y x = D ．2xy =-4．已知1tan 3θ=，那么πtan ()4θ+等于 A ．2 B ．2- C ．12D ． 12-5. 要得到函数sin(2)3y x π=-的图象，只需将函数sin 2y x =的图象A ．向左平移π6个单位 B ．向右平移π6个单位 C ．向左平移π3个单位 D ．向右平移π3个单位6. 下列命题正确的是 A. “1<x ”是“0232>+-x x ”的必要不充分条件B. 若给定命题p ：x ∃∈R ，使得210x x +-<，则p ⌝：,x ∀∈R 均有012≥-+x x C. 若q p ∧为假命题，则q p ,均为假命题D. 命题“若0232=+-x x ，则2=x ”的否命题为“若 ,0232=+-x x 则2≠x7.在ABC ∆中，已知4AB AC ⋅=，3=，,M N 分别是BC 边上的三等分点，则⋅的值是A ．5B ．421C ．6D ．88. 已知函数2,()2.x x x a f x x a ⎧≤<=⎨≥⎩, 0, 若存在实数b ，使函数()()g x f x b =-有两个零点，则实数a的取值范围是A ．(0,2)B ．(2,)+∞C ．(2,4)D ．(4,)+∞第二部分（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上. 9.若集合{}1,0,a ={}1,1,-bc ，则_____,_______.a b ==10.设等差数列{}n a 的前n 项和为n S ，若3612a a +=，48S =，则9a 的值是 ． 11.给出四个命题：①平行于同一平面的两个不重合的平面平行；②平行于同一直线的两个不重合的平面平行；③垂直于同一平面的两个不重合的平面平行；④垂直于同一直线的两个不重合的平面平行；其中真命题的序号是________．12．已知函数()2sin f x x ω=(0>ω)的最小正周期为π，则=ω ，在(0,)π内满足0)(0=x f 的0x ＝ ．13. 若函数()sin cos f x a x x =+在区间ππ(,)64上单调递增，则实数a 的取值范围是 .14.如图，在ABC ∆中，4AB AC ==，90BAC ∠=，D 是BC 的中点，若向量14AM AB mAC=+（m ∈R ），且点M 在ACD ∆的内部（不含边界），则AM BM ⋅的取值范围是 ．三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15. （本小题满分13分）已知函数2()cos 2cos 222x x xf x =+.（Ⅰ）求)(x f 的最小正周期； （Ⅱ）求)(x f 的单调递减区间.16. （本小题满分13分）设等差数列{}n a 的前n 项和为n S ，n *∈N ，公差30,15,d S ≠=已知1341,,a a a 成等比数列. （Ⅰ）求数列{}n a 的通项公式（Ⅱ）设2n n b a =，求数列{}n b 的前n 项和n T . 17. （本小题满分14分）如图, 在三棱柱111ABC A B C -中，1CC ⊥底面ABC ,CB AC ⊥,点D 是AB 的中点．（Ⅰ）求证：1AC BC ⊥； （Ⅱ）求证：1AC ∥平面1CDB .(Ⅲ)设12AB AA =,AC BC =,在线段11A B 上是否存在点M ，使得1BM CB ⊥?若存在,确定点M 的位置;若不存在，说明理由.18. （本小题满分13分）在ABC ∆中，角C B A ,,所对的边分别为c b a ,,．已知21cos -=B ． （Ⅰ）若322==b a ,，求ABC ∆的面积； （Ⅱ）求C A sin sin ⋅的取值范围． 19. （本小题满分13分）已知函数2()ln (1)2x f x a x a x =+-+，a ∈R ．（Ⅰ）若函数()f x 在区间(1,3)上单调递减，求a 的取值范围； （Ⅱ）当1a =-时，证明1()2f x ≥. 20. （本小题满分14分）已知函数2()e (1)x f x a x b x =++(其中a ，b ∈R ),函数()f x 的导函数为()f x '，且(1)0f '-=．(Ⅰ)若1b =，求曲线()y f x =在点(0,(0))f 处的切线方程； (Ⅱ)若函数()f x 在区间[1,1]-上的最小值为0，求b 的值．北京市朝阳区2015-2016学年度高三年级第一学期期中统一考试数学答案（文史类） 2015.11一、选择题：（满分40分）二、填空题：（满分30分）三、解答题：（满分80分） 15. （本小题满分13分） （I ）由已知可得：()cos 1f x x x =++2sin()16x π=++. 所以)(x f 的最小正周期为2π. …………………..7分（II ）由2222k x k ππ3ππ+≤+≤π+6， k ∈Z , 得2233k x k π4ππ+≤≤π+,k ∈Z .因此函数)(x f 的单调递减区间为[2,2]33k k π4ππ+π+,k ∈Z .…………………..13分16. （本小题满分13分） 解：（I ）依题意，1211132315,2(3)(12).a d a d a a d ⨯⎧+=⎪⎨⎪+=+⎩ 解得13,2.a d =⎧⎨=⎩因此1(1)32(1)21,21n n a a n d n n a n =+-=+-=+=+即. …………………..6分 (Ⅱ)依题意，1212212+=+⨯==+n n n n a b .12n n T b b b =+++231(21)(21)(21)n +=++++++=23122...2n n +++++4(12)12n n-=+-22 4.n n +=+- …………………..13分17.（本小题满分14分）（I ）在三棱柱111ABC A B C -中，因为1CC ⊥底面ABC ，AC ⊂底面ABC ， 所以1CC AC ⊥. 又AC BC ⊥，1BCCC C =,所以11AC BCC B ⊥平面． 而111BC BCC B ⊂平面，则1AC BC ⊥. …………………..4分 (Ⅱ)设1CB 与1C B 的交点为E ，连结DE ， 因为D 是AB 的中点，E 是1BC 的中点， 所以DE ∥1AC .因为1DE CDB ⊂平面，11AC CDB ⊄平面， 所以1AC ∥1CDB 平面.E…………………..9分(Ⅲ)在线段11A B 上存在点M ，使得1BM CB ⊥,且M 为线段11A B 的中点.证明如下：因为1AA ⊥底面ABC ，CD ⊂底面ABC ,所以1AA CD ⊥.由已知AC BC =，D 为线段AB 的中点， 所以CD AB ⊥. 又1AA AB A =，所以CD ⊥平面11AA B B .取线段11A B 的中点M ，连接BM . 因为BM ⊂平面11AA B B ，所以CD BM ⊥.由已知12AB AA =，由平面几何知识可得1BM B D ⊥. 又1CDB D D =,所以BM ⊥平面1B CD .又1B C ⊂平面1B CD ， 所以1BM CB ⊥.…………………..14分18. （本小题满分13分）（I ）在ABC ∆中，因为1cos 2B =-，所以2π3B =，sin B =由正弦定理,sin sin a bA B=可得2sin A =则1sin 2A =. 又A 为锐角，则6A π=，所以6C π=. 所以1sin 2ABC S ab C ∆=EM11222=⨯⨯=. .……………………………………………………………6分（II ）sin sin sin()sin 3A C C C π⋅=-⋅=1sin sin )2C C C ⋅-12(1cos2)4C C --11sin(2)264C π=+-. 因为(0,)3C π∈，所以52(,)666C πππ+∈.则1sin(2)(,1]62C π+∈.所以C A sin sin ⋅的取值范围是1(0,]4. ………………………………………13分19. （本小题满分13分） 解：（I ）函数的定义域为(0,)+∞.因为2(1)(1)()()(1)a x a x a x x a f x x a x x x-++--'=+-+==.又因为函数()f x 在(1,3)单调减，所以不等式(1)()0x x a --≤在(1,3)上成立. 设()(1)()g x x x a =--，则(3)0g ≤，即93(1)0a a -++≤即可，解得3a ≥. 所以a 的取值范围是[3,)+∞. …………………………………7分（Ⅱ）当1a =-时，2()ln 2x f x x =-+，211(1)(1)()x x x f x x x x x-+-'=-+==.令()0f x '=，得1x =或1x =-（舍）. 当x 变化时，(),()f x f x '变化情况如下表所以1x =时,函数()f x 的最小值为(1)2f =. 所以1()2f x ≥成立. ………………………………13分20. （本小题满分14分）解：因为2()e (1)xf x ax bx =++，所以2()e [(2)1]xf x ax a b x b '=++++． 因为(1)0f '-=，所以(2)10a a b b -+++=．所以1a =． ……………………2分 (Ⅰ)当1a =时，1b =时， (0)1,(0)2f f '==，所以曲线()y f x =在点(0,(0))f 处的切线方程为12(0)y x -=-．即210x y -+=． ……………………4分 (Ⅱ)由已知得2()e (1)xf x x bx =++，所以2()e [(2)1]e (1)(1)x xf x x b x b x x b '=++++=+++．（1）当11b --<-，即0b >时，令()e (1)(1)0xf x x x b '=+++>得，1x >-或1x b <--； 令()e (1)(1)0x f x x x b '=+++<得，11b x --<<-．所以函数()f x 在(1,)-+∞和(,1)b -∞--上单调递增，在(1,1)b ---上单调递减． 所以函数()f x 在区间[1,1]-上单调递增．所以函数()f x 在区间[1,1]-上的最小值为1(1)e (2)0f b --=-=． 解得2b =．显然合题意． （2）当11b --=-时，即0b =时，2()e (1)0xf x x '=+≥恒成立，所以函数()f x 在(,)-∞+∞上单调递增． 所以函数()f x 在区间[1,1]-上单调递增．所以函数()f x 在区间[1,1]-上的最小值为1(1)e (2)0f b --=-=． 解得2b =．显然不符合题意． （3）当11b -->-时，即0b <时，令()e (1)(1)0xf x x x b '=+++>得，1x <-或1x b >--； 令()e (1)(1)0xf x x x b '=+++<得，11x b -<<--．所以函数()f x 在(,1)-∞-和(1,)b --+∞上单调递增，在(1,1)b ---上单调递减． ①若11b --≥，即2b ≤-时，函数()f x 在区间[1,1]-上单调递减．所以函数()f x 在区间[1,1]-上的最小值为(1)e(2)0f b =+=． 解得2b =-．显然合题意．②若11b --<，即20b -<<时，函数()f x 在在(1,1)b ---上单调递减，在(1,1)b -- 上单调递增．此时，函数()f x 在区间[1,1]-上的最小值为1(1)e(2)0b f b b ----=+=．解得2b =-．显然不合题意．综上所述，2b =或2b =-为所求． ……………………14分。

2015-2016学年北京市东城区高三（上）期中数学试卷（文科）一、选择题1．（5分）如果集合A={﹣1，2}，B={x|x＞0}，那么集合A∩B等于（）A．∅B．{﹣1}C．{2}D．{﹣1，2}2．（5分）命题“∀x∈R，（）x＞0”的否定是（）A．∃x∈R，（）x＜0 B．∀x∈R，（）x≤0 C．∀x∈R，（）x＜0 D．∃x ∈R，（）x≤03．（5分）已知角α的终边经过点P（﹣1，0），则cosα的值为（）A．0 B．﹣1 C．﹣D．4．（5分）下列函数中，其定义域与值域相同的是（）A．y=2x B．y=x2 C．y=log2x D．y=5．（5分）等差数列{a n}的前n项和为S n，已知a3=3，a10=10，则S7的值是（）A．30 B．29 C．28 D．276．（5分）函数f（x）=﹣lnx的零点个数为（）A．0 B．1 C．2 D．37．（5分）三个数a=0.152，b=20.15，c=log20.15之间的大小关系是（）A．c＜a＜b B．c＜b＜a C．a＜b＜c D．b＜c＜a8．（5分）“α≠β”是“sinα≠sinβ”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件9．（5分）函数f（x）=a x﹣（a＞0，a≠1）的图象可能是（）A．B．C．D．10．（5分）已知函数f（x）=sinωx（x∈R，ω＞0）的最小正周期为π，为了得到函数的图象，只要将y=f（x）的图象（）A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度11．（5分）已知函数f（x）=的最大值是2，则实数a的取值范围是（）A．（0，]B．（1，）C．（0，1） D．（0，）12．（5分）已知函数y=Acos（x+φ）（A＞0）在一个周期内的图象如图所示，其中P，Q分别是这段图象的最高点和最低点，M，N是图象与x轴的交点，且∠PMQ=90°，则A的值为（）A．1 B．C．D．2二、填空题13．（5分）若曲线y=ax2﹣lnx在点（1，a）处的切线平行于x轴，则a=．14．（5分）在△ABC中，角A，B所对的边分别为a，b，若a=3bsinA，则sinB=．15．（5分）已知＜α＜π，且tanα=﹣，则sin（α+）=．16．（5分）已知函数f（x）=x3﹣ax2﹣x+a，其中a为实数，若f（x）在x=﹣1处取得极值，则a=．17．（5分）已知函数f（x）=，则f（6）=．18．（5分）在数列{a n}中，已知a1=，a n+1=1﹣，n∈N*，则a30=．三、解答题19．（14分）设函数f（x）=（sinx+cosx）2+cos2x．（Ⅰ）求f（x）的单调递增区间；（Ⅱ）求f（x）在区间[﹣，]上的最大值和最小值．20．（14分）已知等比数列{a n}满足27a2﹣a5=0，a1a2=a3．（Ⅰ）求{a n}的通项公式；（Ⅱ）若b n=3log3a n+3，求证：{b n}是等差数列．21．（15分）已知函数f（x）=为奇函数．（1）求a﹣b的值；（2）若函数f（x）在区间[﹣1，m﹣2]上单调递增，求实数m的取值范围．22．（17分）已知，其中e是无理数，a∈R．（1）若a=1时，f（x）的单调区间、极值；（2）求证：在（1）的条件下，；（3）是否存在实数a，使f（x）的最小值是﹣1，若存在，求出a的值；若不存在，说明理由．2015-2016学年北京市东城区高三（上）期中数学试卷（文科）参考答案与试题解析一、选择题1．（5分）如果集合A={﹣1，2}，B={x|x＞0}，那么集合A∩B等于（）A．∅B．{﹣1}C．{2}D．{﹣1，2}【解答】解：∵A={﹣1，2}，B={x|x＞0}，∴A∩B={2}．故选：C．2．（5分）命题“∀x∈R，（）x＞0”的否定是（）A．∃x∈R，（）x＜0 B．∀x∈R，（）x≤0 C．∀x∈R，（）x＜0 D．∃x ∈R，（）x≤0【解答】解：∵全称命题的否定是特称命题，∴命题“∀x∈R，（）x＞0”的否定是：∃x∈R，（）x≤0，故选：D．3．（5分）已知角α的终边经过点P（﹣1，0），则cosα的值为（）A．0 B．﹣1 C．﹣D．【解答】解：角α的终边经过点P（﹣1，0），则cosα==﹣1，故选：B．4．（5分）下列函数中，其定义域与值域相同的是（）A．y=2x B．y=x2 C．y=log2x D．y=【解答】解：对于A，y=2x的值域为（0，+∞），定义域为R，定义域与值域不同，可排除A；对于B，y=x2的值域为[0，+∞），定义域为R，定义域与值域不同，可排除B；对于C，y=log2x的定义域为（0，+∞），值域为R，定义域与值域不同，可排除C；对于D，y=的定义域为（﹣∞，0）∪（0，+∞），值域为（﹣∞，0）∪（0，+∞），定义域与值域相同，符合题意．故选：D．5．（5分）等差数列{a n}的前n项和为S n，已知a3=3，a10=10，则S7的值是（）A．30 B．29 C．28 D．27【解答】解：由题意，设等差数列的公差为的d，则d==1，故a4=a3+d=4，故S7===7×4=28故选：C．6．（5分）函数f（x）=﹣lnx的零点个数为（）A．0 B．1 C．2 D．3【解答】解：函数f（x）=﹣lnx的零点个数等价于函数y=与函数y=lnx图象交点的个数，在同一坐标系中，作出它们的图象：由图象可知，函数图象有1个交点，即函数的零点个数为1故选：B．7．（5分）三个数a=0.152，b=20.15，c=log20.15之间的大小关系是（）A．c＜a＜b B．c＜b＜a C．a＜b＜c D．b＜c＜a【解答】解：∵0＜a=0.152＜1，b=20.15＞1，c=log20.15＜0，∴b＞a＞c，故选：A．8．（5分）“α≠β”是“sinα≠sinβ”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【解答】解：当α=β时，sinα=sinβ，成立．当，时，满足sinα=sinβ，但α=β不成立，∴sinα=sinβ是α=β的必要不充分条件．根据逆否命题的等价性可知“α≠β”是“sinα≠sinβ”必要不充分条件．故选：B．9．（5分）函数f（x）=a x﹣（a＞0，a≠1）的图象可能是（）A．B．C．D．【解答】解：当0＜a＜1时，函数f（x）=a x﹣，为减函数，当a＞1时，函数f（x）=a x﹣，为增函数，且当x=﹣1时f（﹣1）=0，即函数恒经过点（﹣1，0），故选：D．10．（5分）已知函数f（x）=sinωx（x∈R，ω＞0）的最小正周期为π，为了得到函数的图象，只要将y=f（x）的图象（）A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度【解答】解：由函数f（x）=sinωx（x∈R，ω＞0）的最小正周期为π，可得ω=2则设将y=f（x）的图象向左平行a个单位得到函数的图象则即2a=解得a=故选：C．11．（5分）已知函数f（x）=的最大值是2，则实数a的取值范围是（）A．（0，]B．（1，）C．（0，1） D．（0，）【解答】解：∵f（）==2，且函数f（x）=的最大值是2，∴当x时，log a x≤2恒成立；当a＞1时，log a x≤2不可能恒成立；当0＜a＜1时，log a x≤2恒成立可化为≥a2，即0＜a≤；故选：A．12．（5分）已知函数y=Acos（x+φ）（A＞0）在一个周期内的图象如图所示，其中P，Q分别是这段图象的最高点和最低点，M，N是图象与x轴的交点，且∠PMQ=90°，则A的值为（）A．1 B．C．D．2【解答】解：过Q，P分别作x轴的垂线于B，C，∵函数的周期T==4，∴MN=2，CN=1，∵∠PMQ=90°，∴PQ=2MN=4，即PN=2，则PC==，即A=，故选：C．二、填空题13．（5分）若曲线y=ax2﹣lnx在点（1，a）处的切线平行于x轴，则a=．【解答】解：由题意得，∵在点（1，a）处的切线平行于x轴，∴2a﹣1=0，得a=，故答案为：．14．（5分）在△ABC中，角A，B所对的边分别为a，b，若a=3bsinA，则sinB=．【解答】解：△ABC中，角A，B所对的边分别为a，b，若a=3bsinA，则由正弦定理可得sinA=3sinBsinA，求得sinB=，故答案为：．15．（5分）已知＜α＜π，且tanα=﹣，则sin（α+）=﹣．【解答】解：∵＜α＜π，且tanα=﹣，∴sin（α+）=cosα=﹣=﹣．故答案为：﹣．16．（5分）已知函数f（x）=x3﹣ax2﹣x+a，其中a为实数，若f（x）在x=﹣1处取得极值，则a=﹣1．【解答】解：函数f（x）=x3﹣ax2﹣x+a，可得f′（x）=3x2﹣2ax﹣1，∵f（x）在x=﹣1处取得极值，∴3+2a﹣1=0，∴a=﹣1．故答案为：﹣1．17．（5分）已知函数f （x ）=，则f （6）= 1 ．【解答】解：函数f （x ）=， 则f （6）=f （5）=f （4）==1．故答案为：1．18．（5分）在数列{a n }中，已知a 1=，a n +1=1﹣，n ∈N *，则a 30= 2 ．【解答】解：∵a 1=，a n +1=1﹣，n ∈N *，∴a 2=1﹣2=﹣1，a 3=2，a 4=1﹣=，…， ∴a n +3=a n ． 则a 30=a 3×10=a 3=2， 故答案为：2．三、解答题19．（14分）设函数f （x ）=（sinx +cosx ）2+cos2x ． （Ⅰ）求f （x ）的单调递增区间； （Ⅱ）求f （x ）在区间[﹣，]上的最大值和最小值．【解答】解：（Ⅰ）化简已知函数可得f （x ）=（sinx +cosx ）2+cos2x =1+sin2x +cos2x=1+sin （2x +），由2kπ﹣≤2x +≤2kπ+可得kπ﹣≤x ≤kπ+，∴f （x ）的单调递增区间为：[kπ﹣，kπ+]k ∈Z ； （Ⅱ）∵x ∈[﹣，]，∴2x +∈[﹣，]，∴当2x +=即x=时，f （x ）有最大值+1，当2x +=﹣即x=﹣时，f （x ）有最小值﹣+120．（14分）已知等比数列{a n }满足27a 2﹣a 5=0，a 1a 2=a 3．（Ⅰ）求{a n}的通项公式；（Ⅱ）若b n=3log3a n+3，求证：{b n}是等差数列．【解答】（Ⅰ）解：∵等比数列{a n}满足27a2﹣a5=0，a1a2=a3，∴27a1q﹣a1q4=0，a12q=a1q2，∴a1=3，q=3，∴a n=3n；（Ⅱ）证明：b n=3log3a n+3=3n+3，∴b n﹣b n=3，+1∴{b n}是等差数列．21．（15分）已知函数f（x）=为奇函数．（1）求a﹣b的值；（2）若函数f（x）在区间[﹣1，m﹣2]上单调递增，求实数m的取值范围．【解答】解：（1）令x＜0，则﹣x＞0，则f（x）=﹣f（﹣x）=﹣[﹣x2﹣2x]=x2+2x．∴a=1，b=2，∴a﹣b=﹣1．（2）f（x）=，即有f（x）在[﹣1，1]上递增，由于函数f（x）在区间[﹣1，m﹣2]上单调递增，∴[﹣1，m﹣2]⊆[﹣1，1]，∴，解得，1＜m≤3．22．（17分）已知，其中e是无理数，a∈R．（1）若a=1时，f（x）的单调区间、极值；（2）求证：在（1）的条件下，；（3）是否存在实数a，使f（x）的最小值是﹣1，若存在，求出a的值；若不存在，说明理由．【解答】解：（1）∵当a=1时，，∴，（1分）∴当0＜x＜1时，f'（x）＜0，此时f（x）单调递减当1＜x＜e时，f'（x）＞0，此时f（x）单调递增，（3分）∴f（x）的单调递减区间为（0，1）；单调递增区间为（1，e）；f（x）的极小值为f（1）=1．（4分）（2）由（1）知f（x）在（0，e]上的最小值为1，（5分）令h（x）=g（x）+，x∈（0，e]∴，（6分）当0＜x＜e时，h′（x）＞0，h（x）在（0，e]上单调递增，（7分）∴，∴在（1）的条件下，f（x）＞g（x）+，（8分）（3）假设存在实数a，使，（x∈（0，e]）有最小值﹣1，∴，（9分）①当a≤0时，∵0＜x≤e，∴f'（x）＞0，∴f（x）在（0，e]上单调递增，此时f（x）无最小值．（10分）②当0＜a＜e时，若0＜x＜a，则f'（x）＜0，故f（x）在（0，a）上单调递减，若a＜x＜e，则f'（x）＞0，故f（x）在（a，e]上单调递增.，得，满足条件．（12分）③当a≥e时，∵0＜x＜e，∴f'（x）＜0，∴f（x）在（0，e]上单调递减，（舍去），所以，此时无解．（13分）综上，存在实数，使得当x∈（0，e]时f（x）的最小值是﹣1．（14分）（3）法二：假设存在实数a，使，x∈（0，e]）的最小值是﹣1，故原问题等价于：不等式，对x∈（0，e]恒成立，求“等号”取得时实数a的值．即不等式a≥﹣x（1+lnx），对x∈（0，e]恒成立，求“等号”取得时实数a的值．设g（x）=﹣x（1+lnx），即a=g（x）max，x∈（0，e]（10分）又（11分）令当，g'（x）＞0，则g（x ）在单调递增；当，g'（x）＜0，则g（x ）在单调递减，（13分）故当时，g（x ）取得最大值，其值是故．综上，存在实数，使得当x∈（0，e]时f（x）的最小值是﹣1．（14分）赠送—高中数学知识点【1.3.1】单调性与最大（小）值（1）函数的单调性②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数．③对于复合函数[()]y f g x =，令()u g x =，若()y f u =为增，()u g x =为增，则[()]y f g x =为增；若()y f u =为减，()u g x =为减，则[()]y f g x =为增；若()y f u =为增，()u g x =为减，则[()]y f g x =为减；若()y f u =为减，()u g x =为增，则[()]y f g x =为减． （2）打“√”函数()(0)af x x a x=+>的图象与性质 ()f x分别在(,-∞、)+∞上为增函数，分别在[,0)a -、]a 上为减函数．（3）最大（小）值定义①一般地，设函数()y f x =的定义域为I ，如果存在实数M 满足：（1）对于任意的x I ∈，都有()f x M ≤； （2）存在0x I ∈，使得0()f x M =．那么，我们称M 是函数()f x 的最大值，记作max ()f x M =．②一般地，设函数()y f x =的定义域为I ，如果存在实数m 满足：（1）对于任意的x I ∈，都有()f x m ≥；（2）存在0x I ∈，使得0()f x m =．那么，我们称m 是函数()f x 的最小值，记作max ()f x m =．【1.3.2】奇偶性（4）函数的奇偶性①定义及判定方法yxo②若函数()f x 为奇函数，且在0x =处有定义，则(0)0f =．③奇函数在y 轴两侧相对称的区间增减性相同，偶函数在y 轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．。

北京市朝阳区2016-2017学年度高三年级第一学期统一考试数学试卷（理工类） 2016．11（考试时间120分钟 满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．1．已知全集U =R ，集合{}2|20A x x x =-<，{}|10B x x =-≥，则()U AB =ðA ．{}|01x x <<B ．{}|0x x <C ．{}|2x x >D ．{}|12x x <<2．下列函数中，在其定义域上既是偶函数又在(0)+∞，上单调递减的是 A ．2y x =B ．1y x =+C ．lg ||y x =-D ．2x y =-3．若 2.1log 0.6a =，0.62.1b =，0.5log 0.6c =，则a ，b ，c 的大小关系是 A ．a b c >> B ．b c a >> C ．c b a >> D ．b a c >>4．已知函数2()f x ax x =-，若对任意12,[2,)x x ∈+∞，且12x x ≠，不等式1212()()0f x f x x x ->-恒成立，则实数a 的取值范围是A ．1(,)2+∞B ．1[,)2+∞C ．1(,)4+∞D ．1[,)4+∞ 5．设R m ∈且0m ≠，“不等式4+4m m>”成立的一个充分不必要条件是 A ．0m > B ．1m > C ．2m > D ．2m ≥ 6．已知三角形ABC 外接圆O 的半径为1（O 为圆心），且2OA AB AC ++=0，||2||OA AB =，则CA BC ⋅等于A ．154-B．C ．154 D7．已知函数21,0,()log ,0,x x f x x x +≤⎧=⎨>⎩则函数1()(())2g x f f x =-的零点个数是A ．4B ．3C ．2D ．18. 5个黑球和4个白球从左到右任意排成一排，下列说法正确的是A ．总存在一个黑球，它右侧的白球和黑球一样多B ．总存在一个白球，它右侧的白球和黑球一样多C ．总存在一个黑球，它右侧的白球比黑球少一个D ．总存在一个白球，它右侧的白球比黑球少一个第二部分（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上． 9．已知平面向量(1,2),(2,)y ==-a b .若a //b ，则y = .10．函数22()cos sin f x x x =-的单调递减区间为 .11．各项均为正数的等比数列{}n a 的前n 项和为n S .若23=a ，245S S =，则1a = ，4S = ．12．已知角A 为三角形的一个内角，且3cos 5A =，则t a n A = ，tan()4A π+= .13．已知函数221,0,()(1)2,0xmx x f x m x ⎧+≥=⎨-<⎩在(,)-∞+∞上是具有单调性，则实数m 的取值范围 .14．《九章算术》是我国古代一部重要的数学著作，书中有如下问题:“今有良马与驽马发长安，至齐．齐去长安三千里，良马初日行一百九十三里，日增一十三里，驽马初日行九十七里，日减半里．良马先至齐，复还迎驽马，问几何日相逢．”其大意为：“现在有良马和驽马同时从长安出发到齐去，已知长安和齐的距离是3000里，良马第一天行193里，之后每天比前一天多行13里，驽马第一天行97里，之后每天比前一天少行0.5里．良马到齐后，立刻返回去迎驽马，多少天后两马相遇．”试确定离开长安后的第 天，两马相逢．DCA三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题满分13分）已知数列{}()N n a n *∈是公差不为0的等差数列，11a =，且248111,,a a a 成等比数列.（Ⅰ）求数列{}n a 的通项公式； （Ⅱ）设数列11{}n n a a +⋅的前n 项和为n T ，求证:1n T <.16．（本小题满分13分）已知函数()sin f x a x x =（a ∈R ）的图象经过点(,0)3π. （Ⅰ）求()f x 的最小正周期； （Ⅱ）若3[,]22x ππ∈，求()f x 的取值范围.17．（本小题满分13分）如图，已知,,,A B C D 四点共面，=1CD ,2BC =,4AB =,120ABC ∠=,cos 7BDC ∠=. （Ⅰ）求sin DBC ∠的值； （Ⅱ）求AD 的长.18． （本小题满分13分）已知函数2()cos 4x f x ax x =-+()R a ∈，ππ[,]22x ∈-． （Ⅰ）若函数()f x 是偶函数，试求a 的值；（Ⅱ）当0a >时，求证：函数()f x 在π(0,)2上单调递减.19．（本小题满分14分）已知函数2()e ()xf x x a =-，a ∈R ．（Ⅰ）当1a =时，求曲线()y f x =在点(0,(0))f 处的切线方程； （Ⅱ）若函数()f x 在(3,0)-上单调递减，试求a 的取值范围； （Ⅲ）若函数()f x 的最小值为2e -，试求a 的值．20．（本小题满分14分）设b a ,是正奇数，数列}{n c （n *∈N ）定义如下：b c a c ==21,，对任意3≥n ，nc 是21--+n n c c 的最大奇约数．数列}{n c 中的所有项构成集合A ． （Ⅰ）若15,9==b a ，写出集合A ；（Ⅱ）对1≥k ，令221=max {,}k k k d c c -(max{,}p q 表示,p q 中的较大值），求证：k k d d ≤+1；（Ⅲ）证明集合A 是有限集，并写出集合A 中的最小数．北京市朝阳区2016-2017学年度第一学期高三年级统一考试数学答案（理工类） 2016．11一、选择题：（满分40分）二、填空题：（满分30分）（注：两空的填空，第一空3分，第二空2分） 三、解答题：（满分80分） 15．（本小题满分13分） 解：（Ⅰ）设{}n a 的公差为d ．因为248111,,a a a 成等比数列，所以2428111()a a a =⋅．即2111111()37a d a d a d=⋅+++ ．化简得2111(3)()(7)a d a d a d +=+⋅+，即21d a d =．又11a =，且0d ≠，解得1d = ．所以有1(1)n a a n d n =+-=． …………………7分（Ⅱ）由（Ⅰ）得：11111(1)1nn a a n n n n +==-⋅⋅++．所以11111111122311n T n n n =-+-++-=-<++ ． 因此，1n T <． …………………13分 16．（本小题满分13分）解：（Ⅰ）因为函数()sin f x a x x =的图象经过点(,0)3π，所以 ()0.3f π==解得 1a = ． …………………3分所以()sin 2sin()3f x x x x π==-．所以()f x 最小正周期为2π． …………………6分 （Ⅱ）因为322x ππ≤≤，所以7.636x πππ≤-≤所以当32x ππ-=，即56x π=时，()f x 取得最大值，最大值是2；当736x ππ-=，即32x π=时，()f x 取得最小值，最小值是 1.-所以()f x 的取值范围是[1,2]-． …………………13分 17．（本小题满分13分）解：（Ⅰ）在△BDC 中，因为cos BDC ∠=sin BDC ∠=． 由正弦定理=sin sin DC BCDBC BDC∠∠得，sin sin =DC BDC DBC BC ⋅∠∠= …………5分（Ⅱ）在△BDC 中，由2222cos BC DC DB DC DB BDC =+-⋅⋅∠得，2412DB DB =+-⋅．所以230DB DB --=． 解得DB =DB =． 又因为cos =cos 120ABD DBC （）∠-∠=cos120cos sin120sin DBC DBC ⋅∠+⋅∠1=2-+=-在△ABD 中，因为222=2cos AD AB BD AB BD ABD +-⋅⋅∠=16724(27+-⨯=，所以AD =． …………13分18．（本小题满分13分）解：（Ⅰ）因为函数()f x 是偶函数，所以22()()()cos()cos 44x x f x a x x ax x --=--+-=++ 2()cos 4x f x ax x ==-+恒成立．所以0a =． …………………4分（Ⅱ）由题意可知()sin 2xf x x a '=--． 设()sin 2xg x x a =--，则1()cos 2g x x '=-．注意到π(0,)2x ∈，0a >．由()0g x '<，即1cos 02x -<，解得π03x <<．由()0g x '>，即1cos 02x ->，解得ππ32x <<．所以()g x 在π(0,)3单调递减，ππ(,)32单调递增．所以当π(0,)3x ∈，()(0)00g x g a <=-<，所以()f x 在π(0,)3x ∈单调递减，当ππ(,)32x ∈，ππ()()1024g x g a <=--<，所以()f x 在ππ(,)32x ∈单调递减，所以当0a >时，函数()f x 在π(0,)2上单调递减. ……………………13分19．（本小题满分14分）解：由题意可知2()e (2)xf x x x a '=+-． （Ⅰ）因为1a =，则(0)1f =-，(0)1f '=-，所以函数()f x 在点(0,(0))f 处的切线方程为(1)(0)y x --=--．即10x y ++=． …………………3分 （Ⅱ）因为函数()f x 在(3,0)-上单调递减，所以当(3,0)x ∈-时，2()e (2)0x f x x x a '=+-≤恒成立．即当(3,0)x ∈-时，220x x a +-≤恒成立．显然，当(3,1)x ∈--时，函数2()2g x x x a =+-单调递减，当(1,0)x ∈-时，函数2()2g x x x a =+-单调递增． 所以要使得“当(3,0)x ∈-时，220x x a +-≤恒成立”， 等价于(3)0,(0)0.g g -≤⎧⎨≤⎩即3,0.a a ≥⎧⎨≥⎩所以3a ≥． …………………8分（Ⅲ）设2()2g x x x a =+-，则44a ∆=+．①当440a ∆=+≤，即1a ≤-时，()0g x ≥，所以()0f x '≥． 所以函数()f x 在(,)-∞+∞单增，所以函数()f x 没有最小值．②当440a ∆=+>，即1a >-时，令2()e (2)0xf x x x a '=+-=得220x x a +-=，解得1211x x =-=-随着x 变化时，()f x 和()f x '的变化情况如下：当x ∈( , 1-∞-时，22( 12x a ≥-=++.所以220x a -≥+. 所以2()e ()0xf x x a =->. 又因为函数()f x 的最小值为2e<0-，所以函数()f x 的最小值只能在21x =-处取得.所以121(1e 1]2e 2e f a ---=--==-.所以1e 1)e -=.11=.解得3a =． …………………………………14分 以下证明解的唯一性，仅供参考：设1()e g a -=因为0a >，所以0->，10<．设0x =->，则1x -= 设()e xh x x =-，则()e (1)xh x x '=-+.当0x >时，()0h x '<，从而易知()g a 为减函数. 当(0,3)a ∈，()0g a >；当(3,)a ∈+∞，()0g a <．所以方程1e 1)e -=只有唯一解3a =．20．（本小题满分14分）解：（Ⅰ）数列}{n c 为：9，15，3，9，3，3，3，……．故集合}3,15,9{=A ． ……………3分 （Ⅱ）证明：由题设，对3≥n ，2-n c ，1-n c 都是奇数，所以21--+n n c c 是偶数．从而21--+n n c c 的最大奇约数221--+≤n n n c c c ， 所以},m ax {21--≤n n n c c c ，当且仅当21--=n n c c 时等号成立． 所以，对1≥k 有k k k k d c c c =≤-+},m ax {12212，且k k k k k k d d d c c c =≤≤++},m ax {},m ax {21222．所以k k k k d c c d ≤=+++},m ax {12221，当且仅当122-=k k c c 时等号成立．………9分（Ⅲ）由（Ⅱ）知，当3≥n 时，有},m ax {21--≤n n n c c c ． 所以对3≥n ，有12max max {,}{,}n c c c a b ≤=． 又n c 是正奇数，且不超过max {,}a b 的正奇数是有限的， 所以数列}{n c 中的不同项是有限的． 所以集合A 是有限集．集合A 中的最小数是b a ,的最大公约数． ……………14分。

北京市朝阳区2015-2016学年度高三年级第一学期期中统一考试数学试卷（理工类） 2015.11（考试时间120分钟 满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.1．已知集合{3,}A x x x =≤∈R ，{10,}B x x x =-≥∈N ，则AB =（ ）A ．{0,1}B ．{0,12},C ．{2,3}D ． {1,2,3}2．已知(0,)α∈π，且3cos 5α=-，则tan α=（ ）A ．34B ．34-C ．43D ．43-3. 已知等差数列{}n a 的公差为2，若124, , a a a 成等比数列，那么1a 等于（ ） A. 2 B. 1 C. 1- D. 2-4. 给出下列命题：①若给定命题p ：x ∃∈R ，使得210x x +-<，则p ⌝：,x ∀∈R 均有012≥-+x x ； ②若q p ∧为假命题，则q p ,均为假命题；③命题“若0232=+-x x ，则2=x ”的否命题为“若 ,0232=+-x x 则2≠x ， 其中正确的命题序号是（ ）A ．① B. ①② C. ①③ D. ②③5.已知函数()sin()(00)2f x A x x A ωϕωϕπ=+∈>><R ，，，的图象（部分）如图所示，则()f x 的解析式是（ ）A ．()2sin()6f x x π=π+B ．()2sin(2)6f x x π=π+ C ．()2sin()3f x x π=π+ D ．()2sin(2)3f x x π=π+6.设p ：2101x x -≤-，q ：2(21)(1)0x a x a a -+++<，若p 是q 的充分不必要条件，则实数a 的取值范围是（ ）A ．1(0,)2B ．1[0,)2C ．1(0,]2D ．1[,1)27.在ABC ∆中，已知4AB AC ⋅=3=，,M N 分别是BC 边上的三等分点，则AM ⋅的值是A ．5B ．421C ．6D ．88.已知定义在R 上的函数⎩⎨⎧-∈-∈+=),0 ,1[,2),1 ,0[,2)(22x x x x x f 且)()2(x f x f =+．若方程()2=0f x kx --有三个不相等的实数根，则实数k 的取值范围是（ ）A ．1(,1)3B ．11(,)34--C ．11(,1)(1,)33--D ．1111(,)(,)3443--第二部分（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上. 9.已知三个数π221(),log 3,log π2，其中最大的数是 ．10．已知平面向量2113()(-)，，，a =b =．若向量()λ⊥a a +b ，则实数λ的值是 ．11．如图，在ABCD 中，E 是CD 中点，BE xAB y AD =+，则x y += ．12.若函数()2sin()f x x ωϕ=+(0,0ωϕ≠>)是偶函数，则ϕ的最小值为 ． 13. 若函数sin ()cos a x f x x -=在区间ππ(,)63上单调递增，则实数a 的取值范围是 .14. 如图，已知边长为4的正方形ABCD ，E 是BC 边上一动点（与B 、C 不BE x =，记重合），连结AE ，作EF ⊥AE 交∠BCD 的外角平分线于F .设()f x EC CF =⋅，则函数()f x 的值域是 ；当ECF ∆面积最大时，EF = .三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15. （本小题满分13分）已知函数2()cos2cos 222xx x f x =-. （Ⅰ）求π()3f 的值；（Ⅱ）求函数)(x f 的单调递减区间及对称轴方程.16. （本小题满分13分）已知等差数列{}n a 的首项11a =，公差1d =，前n 项和为n S ，且1n nb S =. （Ⅰ）求数列{}n b 的通项公式； （Ⅱ）求证：1232n b b b b ++++<.17．（本小题满分13分）在ABC ∆中，角C B A ,,所对的边分别为c b a ,,．且21cos -=B ． （Ⅰ）若322==b a ,，求角C ； （Ⅱ）求C A sin sin ⋅的取值范围．FEDCBA18. （本小题满分13分）已知函数2()ln (1)2x f x a x a x =+-+． （Ⅰ）当0a >时，求函数()f x 的单调区间;（Ⅱ）当1a =-时，证明1()2f x ≥.19. （本小题满分14分）已知函数2()e (1)xf x ax bx -=++(其中e 是常数，0a >，b ∈R )，函数()f x 的导函数为()f x '，且(1)0f '-=．(Ⅰ)若1a =，求曲线()y f x =在点(0,(0))f 处的切线方程；(Ⅱ)当15a >时，若函数()f x 在区间[1,1]-上的最大值为4e ，试求,ab 的值．20. （本小题满分14分）已知实数数列}{n a 满足：),2,1(||12 =-=++n a a a n n n ，b a a a ==21,，记集合{|}.n M a n *=∈N （Ⅰ）若2,1==b a ，用列举法写出集合M ；（Ⅱ）若0,0<<b a ，判断数列}{n a 是否为周期数列，并说明理由； （Ⅲ）若0,0≥≥b a ，且0≠+b a ，求集合M 的元素个数的最小值.。

Ⅰ． Teaching Aims and Demands 1． Knowledge Objects （1） Key Vocabulary oversleep （2） Target Language What happened? I overslept． And by the time I got up, my brother had already gotten in the shower． 2． Ability Objects （1） Teach the students to use the new words． （2） Train the students to narrate past events with the Past Perfect Tense． （3） Train the students’ listening and speaking skills with the target language． 3． Moral Object It’s a good habit to go to bed early in the evening and get up early in the morning． So you’ll never be in a hurry in the morning． ． Teaching Key Points 1． Key Vocabulary oversleep 2． Target Language Narrate past events with the Past Perfect Tense ． Teaching Difficult Points 1． Train the students to narrate past events with the Past Perfect Tense． 2． Train the students to understand the target language in spoken conversation． ． Teaching Methods 1． Thinking of examples from the students’ real lives． 2． Making sentences by looking at the pictures． ． Teaching Aid A tape recorder ． Teaching Procedures Step I Revision 1． Revise the language points in Unit 8． Ask some questions like this: What volunteer work would you like to do? Help the students to answer, I’d like to…/I love to…/I hope to… 2． Practice the dialogue in Activity 3c on page 62 again． Get students to role play the similar dialogues with the following． Step 1a This activity introduces new vocabulary which can be used to narrate past events． Write By the time I came back…on the blackboard． Say to the class, By the time I came in． what had happened? Help one student to answer like this, By the time the teacher came in, Don had written his name on the blackboard． Then get more students to answer differently, such as, By the lime the teacher came in, we had discussed an English problem． By the time the teacher came in, I had drawn a picture． Write these sentences on the blackboard, and teach the students to read several times． Read the instructions to the students and read these questions to the class as well． What do you usually do in, the morning before school? Do you like morning? Why or why not? Choose one good student to answer them by saying something he or she usually does in the morning． He or she may answer like this, I usually get up early, wash my face and have breakfast． I like mornings because the air is fresh,or I usually get up as late as possible． Then I have to wash my face and have breakfast in a hurry． I often rush to school without breakfast． Sometimes I forget something at home． I don’t like mornings because I am always too busy． Then have the whole class practice in pairs． Ask each other the questions． After they finish talking, ask one or two pairs to say their conversations to the class． Correct the mistakes they may make with the other students． Call the students’ attention to the pictures in Activity la． Ask students to tell what they see． school, she realized she had left her backpack at home． The sentences can vary, but should be correct． Step 1b This activity gives students practice in understanding the target language in spoken conversation． Ask the students to read the instructions together． Have them look at the two columns, A and B ,in the chart． Point out the sample answer． Read the two parts of the sentence． Then go over the other unconnected parts of sentences, too． You will connect the two parts of the sentences, connect a sentence beginning in the first column with the end of that sentence in the second column． Please guess the other two sentences before I play the tape． I guess most of the children can get the correct sentences by guessing． So just let them guess．Don’t tell them whether their answers are right or wrong． OK, just keep your answers by guessing． Let’s decide if they are right by listening to the tape now． Play the recording for the first time． Students only listen． Then play it a second time． Let students match two parts of each sentence．Check the answers by asking some students to tell their answers． Make sure that all of them have got the correct answers by listening． Say congratulations to the students who get the answers correctly by guessing． Step 1c This practice provides guided oral practice using the target language． First play the recording in Activity 1b again and let the students read after it． Do it at least twice． Then read the instructions together with the whole class． You will make conversations in pairs． Each of you will have to take turns being Tina． Look at the pictures in Activity la to help you． Tell your partner what happened to you this morning． Ask a pair to read the example to the class before they begirt SA: What happened? SB: I overslept． And by the time I got up, my brother had already gotten in the shower． Write the conversation on the blackboard． Have the students work in pairs． Move around the room offering language support as needed． After they all finish talking, ask some pairs to say their conversations to the class． Step Summary Say, In this class, we’ve learned how to narrate past events, using the Past Perfect Tense． We’ve also done some listening practice in understanding the target language in spoken conversation． Also, we’ve done much oral practice using the target language． Step Homework 1． Write out the story of Tina, Note to use the target language． 2． Revise when to use the Past Perfect Tense and the verb structure of it． Step Blackboard Design Unit 9 By the time I got outside, the bus had already left． Section A The First Period 1． By the time… By the time the teacher came in, the students had begun reading． By the time the teacher came in, Don had written his name on the blackboard． By the time the teacher came m, we had discussed an English problem． 2． Some words to describe the pictures overslept, taking a shower, had left, left her backpack at home． 3． Target Language: A: What happened? B:I overslept． And by the time I got up, my brother had already gotten in the shower．。

2016-2017学年北京市朝阳区高三（上）期中数学试卷（文科）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.1．已知集合A={x|x（x﹣1）＜0，x∈R}，B={x|＜x＜2，x∈R}，那么集合A∩B=（）A．∅B．C．{x|﹣2＜x＜2，x∈R}D．{x|﹣2＜x＜1，x∈R}2．下列四个函数中，在其定义域上既是奇函数又是单调递增函数的是（）A．y=x﹣1 B．y=tanx C．y=x3D．3．已知sinx=，则sin2x的值为（）A．B．C．或D．或﹣4．设x∈R且x≠0，则“x＞1”是“x+＞2”成立的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件5．设m，n是两条不同的直线，α，β是两个不同的平面．下列命题正确的是（）A．若m⊂α，n⊂β，m⊥n，则α⊥βB．若α∥β，m⊥α，n∥β，则m⊥nC．若α⊥β，m⊥α，n∥β，则m∥n D．若α⊥β，α∩β=m，n⊥m，则n⊥β6．已知三角形ABC外接圆O的半径为1（O为圆心），且+=，||=2||，则•等于（）A．B．C．D．7．已知函数f（x）=则函数g（x）=f（f（x））﹣的零点个数是（）A．4 B．3 C．2 D．18．5个黑球和4个白球从左到右任意排成一排，下列说法正确的是（）A．总存在一个黑球，它右侧的白球和黑球一样多B．总存在一个白球，它右侧的白球和黑球一样多C．总存在一个黑球，它右侧的白球比黑球少一个D．总存在一个白球，它右侧的白球比黑球少一个二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上.9．设平面向量=（1，2），=（﹣2，y），若∥，则y=．10．已知角A为三角形的一个内角，且cosA=，sinA=．cos2A=．11．已知a=log2.10.6，b=2.10.6，c=log0.50.6，则a，b，c的大小关系是．12．各项均为正数的等比数列{{a n}的前n项和为S n，若a3=2，S4=5S2，则a1的值为，S4的值为．13．已知函数f（x）=在（﹣∞，+∞）上是具有单调性，则实数m的取值范围．14．《九章算术》是我国古代一部重要的数学著作，书中有如下问题：“今有良马与驽马发长安，至齐．齐去长安三千里，良马初日行一百九十三里，日增一十三里，驽马初日行九十七里，日减半里．良马先至齐，复还迎驽马，问几何日相逢．”其大意为：“现在有良马和驽马同时从长安出发到齐去，已知长安和齐的距离是3000里，良马第一天行193里，之后每天比前一天多行13里，驽马第一天行97里，之后每天比前一天少行0.5里．良马到齐后，立刻返回去迎驽马，多少天后两马相遇．”试确定离开长安后的第天，两马相逢．三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15．已知数列{a n}（n∈N*）是公差不为0的等差数列，若a1=1，且a2，a4，a8成等比数列．（Ⅰ）求{a n}的通项公式；（Ⅱ）若b n=，求数列{b n}的前n项和S n．16．已知函数f（x）=asinx﹣cosx（a∈R）的图象经过点（，0）．（Ⅰ）求f（x）的最小正周期；（Ⅱ）若x∈[，]，求f（x）的取值范围．17．如图，已知A，B，C，D四点共面，且CD=1，BC=2，AB=4，∠ABC=120°，cos∠BDC=．（Ⅰ）求sin∠DBC；（Ⅱ）求AD．18．如图，四边形ABCD为矩形，PA⊥平面ABCD，DE∥PA．（Ⅰ）求证：BC⊥CE；（Ⅱ）若直线m⊂平面PAB，试判断直线m与平面CDE的位置关系，并说明理由；（Ⅲ）若AB=PA=2DE=2，AD=3，求三棱锥E﹣PCD的体积．19．已知函数f（x）=，a∈R．（Ⅰ）若曲线y=f（x）在点（0，f（0））处切线斜率为﹣2，求函数f（x）的最小值；（Ⅱ）若函数f（x）在区间（0，1）上无极值，求a的取值范围．20．已知函数f（x）=ax﹣﹣（a+1）lnx，a∈R．（I）若a=﹣2，求函数f（x）的单调区间；（Ⅱ）若a≥1，且f（x）＞1在区间[，e]上恒成立，求a的取值范围；（III）若a＞，判断函数g（x）=x[f（x）+a+1]的零点的个数．2016-2017学年北京市朝阳区高三（上）期中数学试卷（文科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.1．已知集合A={x|x（x﹣1）＜0，x∈R}，B={x|＜x＜2，x∈R}，那么集合A∩B=（）A．∅B．C．{x|﹣2＜x＜2，x∈R}D．{x|﹣2＜x＜1，x∈R}【考点】交集及其运算．【分析】化简集合A，根据交集的定义求出A∩B即可．【解答】解：集合A={x|x（x﹣1）＜0，x∈R}={x|0＜x＜1，x∈R}，B={x|＜x＜2，x∈R}，集合A∩B={x|＜x＜1，x∈R}．故选：B．2．下列四个函数中，在其定义域上既是奇函数又是单调递增函数的是（）A．y=x﹣1 B．y=tanx C．y=x3D．【考点】函数奇偶性的判断．【分析】根据函数奇偶性和单调性的性质分别进行判断即可．【解答】解：A．f（x）=x﹣1是非奇非偶函数，不满足条件．B．y=tanx是奇函数，在定义域上函数不是单调函数，不满足条件．C．y=x3是奇函数，在定义域上为增函数，满足条件．D.是奇函数，在定义域上不是单调函数，不满足条件．故选：C3．已知sinx=，则sin2x的值为（）A．B．C．或D．或﹣【考点】二倍角的正弦．【分析】由已知利用同角三角函数基本关系式可求cosx，进而利用二倍角的正弦函数公式即可计算求值．【解答】解：∵sinx=，∴cosx=±=±，∴sin2x=2sinxcosx=2×（±）=±．故选：D．4．设x∈R且x≠0，则“x＞1”是“x+＞2”成立的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据基本不等式的性质，结合充分不必要条件的定义进行判断即可．【解答】解：当x＜0时，不等式x+＞2不成立，当x＞0时，x+≥2=2，当且仅当x=，即x=1时，取等号，当x＞1时，不等式x+＞2成立，反之不一定成立，是充分不必要条件，故选：A5．设m，n是两条不同的直线，α，β是两个不同的平面．下列命题正确的是（）A．若m⊂α，n⊂β，m⊥n，则α⊥βB．若α∥β，m⊥α，n∥β，则m⊥nC．若α⊥β，m⊥α，n∥β，则m∥n D．若α⊥β，α∩β=m，n⊥m，则n⊥β【考点】空间中直线与平面之间的位置关系．【分析】在A中，α与β相交或平行；在B中，推导出m⊥β，所以m⊥n；在C中，m与n相交、平行或异面；在D中，n与β相交、平行或n⊂β．【解答】解：由m，n是两条不同的直线，α，β是两个不同的平面，知：在A中，若m⊂α，n⊂β，m⊥n，则α与β相交或平行，故A错误；在B中，若α∥β，m⊥α，n∥β，则m⊥β，所以m⊥n，故B正确；在C中，若α⊥β，m⊥α，n∥β，则m与n相交、平行或异面，故C错误；在D中，若α⊥β，α∩β=m，n⊥m，则n与β相交、平行或n⊂β，故D错误．故选：B．6．已知三角形ABC外接圆O的半径为1（O为圆心），且+=，||=2||，则•等于（）A．B．C．D．【考点】平面向量数量积的运算．【分析】由题意可得三角形是以角A为直角的直角三角形，解直角三角形求出相应的边和角，代入数量积公式得答案．【解答】解：三角形ABC外接圆O的半径为1（O为圆心），且+=，∴O为BC的中点，故△ABC是直角三角形，∠A为直角．又||=2||，∴||=，||=2，∴||=，∴cosC===，∴•=﹣•=﹣×2×=﹣故选：A．7．已知函数f（x）=则函数g（x）=f（f（x））﹣的零点个数是（）A．4 B．3 C．2 D．1【考点】函数零点的判定定理．【分析】作出函数的图象，先求出f（x）=的根，然后利用数形结合转化为两个函数的交点个数即可．【解答】解：作出函数f（x）的图象如图：当x≤0时，由f（x）=得x+1=，即x=﹣1=﹣，当x＞0时，由f（x）=得log2x=，即x==，由g（x）=f（f（x））﹣=0得f（f（x））=，则f（x）=﹣或f（x）=，若f（x）=﹣，此时方程f（x）=﹣有两个交点，若f（x）=，此时方程f（x）=只有一个交点，则数g（x）=f（f（x））﹣的零点个数是3个，故选：B8．5个黑球和4个白球从左到右任意排成一排，下列说法正确的是（）A．总存在一个黑球，它右侧的白球和黑球一样多B．总存在一个白球，它右侧的白球和黑球一样多C．总存在一个黑球，它右侧的白球比黑球少一个D．总存在一个白球，它右侧的白球比黑球少一个【考点】进行简单的合情推理．【分析】5个黑球和4个白球，5为奇数，4为偶数，分析即可得到答案．【解答】解：5为奇数，4为偶数，故总存在一个黑球，它右侧的白球和黑球一样多，故选：A二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上.9．设平面向量=（1，2），=（﹣2，y），若∥，则y=﹣4．【考点】平行向量与共线向量．【分析】直接利用向量共线的坐标表示列式计算【解答】解：∵=（1，2），=（﹣2，y），∥，∴1×y=2×（﹣2）∴y=﹣4故答案为：﹣410．已知角A为三角形的一个内角，且cosA=，sinA=．cos2A=﹣．【考点】同角三角函数基本关系的运用；二倍角的余弦．【分析】利用同角三角函数的基本关系，二倍角的余弦公式，求得sinA和cos2A的值．【解答】解：∵角A为三角形的一个内角，且cosA=，∴sinA==，cos2A=2cos2A﹣1=2•﹣1=﹣，故答案为：．11．已知a=log2.10.6，b=2.10.6，c=log0.50.6，则a，b，c的大小关系是b＞c＞a．【考点】对数值大小的比较．【分析】直接利用中间量“0”，“1”判断三个数的大小即可．【解答】解：a=log2.10.6＜0，b=2.10.6＞1，0＜c=log0.50.6＜1∴b＞c＞a，故答案为：b＞c＞a．12．各项均为正数的等比数列{{a n}的前n项和为S n，若a3=2，S4=5S2，则a1的值为，S4的值为．【考点】等比数列的前n项和．【分析】经分析等比数列为非常数列，设出等比数列的公比，有给出的条件列方程组求出a1和q的值，则S4的值可求．【解答】解：若等比数列的公比等于1，由a3=2，则S4=4a3=4×2=8，5S2=5×2S3=5×2×2=20，与题意不符．设等比数列的公比为q（q≠1），由a3=2，S4=5S2，得：，整理得，解得，q=±2．因为数列{a n}的各项均为正数，所以q=2．则．故答案为；．13．已知函数f（x）=在（﹣∞，+∞）上是具有单调性，则实数m的取值范围（1，] ．【考点】函数单调性的性质．【分析】函数f（x）在（﹣∞，+∞）上是具有单调性，需要对m分类讨论，当m＞1，m＜﹣1，m=±1、0，﹣1＜m＜0，0＜m＜1分别判断分段函数的单调性．【解答】解：令h（x）=mx2+1，x≥0；g（x）=（m2﹣1）2x，x＜0；①当m＞1时，要使得f（x）在（﹣∞，+∞）上是具有单调性，即要满足m2﹣1≤1⇒﹣≤m≤故：1＜m≤；②当m＜﹣1时，h（x）在x≥0上递减，g（x）在x＜0上递增，所以，f（x）在R上不具有单调性，不符合题意；③当m=±1时，g（x）=0；当m=0时，h（x）=1；所以，f（x）在R上不具有单调性，不符合题意；④当﹣1＜m＜0 时，h（x）在x≥0上递减，g（x）在x＜0上递减，对于任意的x≥0，g（x）＜0；当x→0时，h（x）＞0；所以，f（x）在R上不具有单调性，不符合题意；⑤当0＜m＜1时，h（x）在x≥0上递增，g（x）在x＜0上递减；所以，f（x）在R上不具有单调性，不符合题意；故答案为：（1，]14．《九章算术》是我国古代一部重要的数学著作，书中有如下问题：“今有良马与驽马发长安，至齐．齐去长安三千里，良马初日行一百九十三里，日增一十三里，驽马初日行九十七里，日减半里．良马先至齐，复还迎驽马，问几何日相逢．”其大意为：“现在有良马和驽马同时从长安出发到齐去，已知长安和齐的距离是3000里，良马第一天行193里，之后每天比前一天多行13里，驽马第一天行97里，之后每天比前一天少行0.5里．良马到齐后，立刻返回去迎驽马，多少天后两马相遇．”试确定离开长安后的第20天，两马相逢．【考点】等差数列的前n项和．【分析】利用等差数列的求和公式与不等式的解法即可得出．【解答】解：由题意知，良马每日行的距离成等差数列，记为{a n}，其中a1=103，d=13；驽马每日行的距离成等差数列，记为{b n}，其中b1=97，d=﹣0.5；设第m天相逢，则a1+a2+…+a m+b1+b2+…+b m=103m++97m+=200m+×12.5≥2×3000，化为m2+31m﹣960≥0，解得m，取m=20．故答案为：20．三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15．已知数列{a n}（n∈N*）是公差不为0的等差数列，若a1=1，且a2，a4，a8成等比数列．（Ⅰ）求{a n}的通项公式；（Ⅱ）若b n=，求数列{b n}的前n项和S n．【考点】数列的求和；数列递推式．【分析】（I）a2，a4，a8成等比数列，可得．再利用等差数列的通项公式即可得出．（Ⅱ）b n==，利用“裂项求和方法”即可得出．【解答】解：（Ⅰ）设{a n}的公差为d，因为a2，a4，a8成等比数列，所以．即，即d2=a1d．又a1=1，且d≠0，解得d=1．所以有a n=a1+（n﹣1）d=1=（n﹣1）=n．（Ⅱ）由（Ⅰ）知：．则．即．16．已知函数f（x）=asinx﹣cosx（a∈R）的图象经过点（，0）．（Ⅰ）求f（x）的最小正周期；（Ⅱ）若x∈[，]，求f（x）的取值范围．【考点】三角函数中的恒等变换应用；正弦函数的图象．【分析】（Ⅰ）根据函数f（x）的图象过点，代入函数解析式求出a的值，从而写出函数解析式并求出最小正周期；（Ⅱ）根据x的取值范围，计算f（x）的最值，从而求出它的取值范围．【解答】解：（Ⅰ）因为函数的图象经过点，所以，解得a=1；…所以，所以f（x）最小正周期为T=2π；…（Ⅱ）因为，所以；所以当，即时，f（x）取得最大值，最大值是2；当，即时，f（x）取得最小值，最小值是﹣1；所以f（x）的取值范围是[﹣1，2]．…17．如图，已知A，B，C，D四点共面，且CD=1，BC=2，AB=4，∠ABC=120°，cos∠BDC=．（Ⅰ）求sin∠DBC；（Ⅱ）求AD．【考点】余弦定理；正弦定理．【分析】（Ⅰ）利用已知及同角三角函数基本关系式可求，进而利用正弦定理即可求得sin∠DBC的值．（Ⅱ）在△BDC中，由余弦定理可求DB的值，利用同角三角函数基本关系式可求，进而利用两角差的余弦函数公式可求cos∠ABD的值，在△ABD中，由余弦定理可求AD的值．【解答】（本小题满分13分）解：（Ⅰ）在△BDC中，因为，所以．由正弦定理得，．…（Ⅱ）在△BDC中，由BC2=DC2+DB2﹣2DC•DBcos∠BDC，得，．所以．解得或（舍）．由已知得∠DBC是锐角，又，所以．所以cos∠ABD=cos=cos120°•cos∠DBC+sin120°•sin∠DBC==．在△ABD中，因为AD2=AB2+BD2﹣2AB•BDcos∠ABD=，所以．…18．如图，四边形ABCD为矩形，PA⊥平面ABCD，DE∥PA．（Ⅰ）求证：BC⊥CE；（Ⅱ）若直线m⊂平面PAB，试判断直线m与平面CDE的位置关系，并说明理由；（Ⅲ）若AB=PA=2DE=2，AD=3，求三棱锥E﹣PCD的体积．【考点】棱柱、棱锥、棱台的体积；空间中直线与直线之间的位置关系．【分析】（Ⅰ）推导出DE⊥BC．，BC⊥CD，由此能证明BC⊥CE．（Ⅱ）推导出DE∥平面PAB，CD∥平面PAB，从而平面PAB∥平面CDE，从而得到m∥平面CDE．（Ⅲ）三棱锥E﹣PCD的体积等于三棱锥P﹣CDE的体积，由此能求出三棱锥E﹣PCD的体积．【解答】（本小题满分14分）证明：（Ⅰ）因为PA⊥底面ABCD，PA∥DE所以DE⊥底面ABCD．所以DE⊥BC．又因为底面ABCD为矩形，所以BC⊥CD．又因为CD∩DE=D，所以BC⊥平面CDE．所以BC⊥CE．…解：（Ⅱ）若直线m⊂平面PAB，则直线m∥平面CDE．证明如下，因为PA∥DE，且PA⊂平面PAB，DE⊄平面PAB，所以DE∥平面PAB．在矩形ABCD中，CD∥BA，且BA⊂平面PAB，CD⊄平面PAB，所以CD∥平面PAB．又因为CD∩DE=D，所以平面PAB∥平面CDE．又因为直线m⊂平面PAB，所以直线m∥平面CDE．…（Ⅲ）由题意知，三棱锥E﹣PCD的体积等于三棱锥P﹣CDE的体积．由（Ⅰ）可知，BC⊥平面CDE．又因为AD∥BC，所以AD⊥平面CDE．易证PA∥平面CDE，所以点P到平面CDE的距离等于AD的长．因为AB=PA=2DE=2，AD=3，所以．所以三棱锥E﹣PCD的体积．…19．已知函数f（x）=，a∈R．（Ⅰ）若曲线y=f（x）在点（0，f（0））处切线斜率为﹣2，求函数f（x）的最小值；（Ⅱ）若函数f（x）在区间（0，1）上无极值，求a的取值范围．【考点】利用导数研究函数的极值；利用导数研究曲线上某点切线方程．【分析】（Ⅰ）先求出函数的导函数令x的值为0代入其中得到f'（0）=﹣2即切线方程的斜率为﹣2，即可求出a的值，再利用导数和函数的最值的关系即可求出最小值，（Ⅱ）求出函数的导函数，f（x）在区间（0，1）上无极值，则函数f（x）在（0，1）单调，分类讨论，求出函数的单调性即可求出a的取值范围【解答】解：（Ⅰ）因为，所以．依题意，f′（0）=﹣2，解得a=﹣1．所以，．当x＞2时，f'（x）＞0，函数f（x）为增函数；当x＜2时，f'（x）＜0，函数f（x）为减函数；所以函数f（x）的最小值是．（Ⅱ）因为，所以．（1）若a=0，则．此时f（x）在（0，1）上单调递减，满足条件．（2）若a≠0，令f'（x）=0得．（ⅰ）若，即0＜a≤1，则f'（x）＜0在（0，1）上恒成立．此时f（x）在（0，1）上单调递减，满足条件．（ⅱ）若，即a＞1时，由f'（x）＞0得；由f'（x）＜0得．此时f（x）在上为增函数，在上为减，不满足条件．（ⅲ）若即a＜0．则f'（x）＜0在（0，1）上恒成立．此时f（x）在（0，1）上单调递减，满足条件．综上，a≤1．20．已知函数f（x）=ax﹣﹣（a+1）lnx，a∈R．（I）若a=﹣2，求函数f（x）的单调区间；（Ⅱ）若a≥1，且f（x）＞1在区间[，e]上恒成立，求a的取值范围；（III）若a＞，判断函数g（x）=x[f（x）+a+1]的零点的个数．【考点】利用导数求闭区间上函数的最值；利用导数研究函数的单调性．【分析】（1）当a=﹣2时，对f（x）求导，求出导函数的零点，即可判断单调区间；（2）若a≥1，且f（x）＞1在区间[，e]上恒成立，即：f（x）在[，e]上的最小值大于1；利用导数求判断函数f（x）的最小值．（3）分类讨论判断g'（x）的单调性与函数的最小值，从而验证g（x）在区间（0，+∞）上单调递增．再构造新函数h（a）=e3a﹣（2lna+6），证明h（a）＞0，进而判断函数g（x）是否穿过x轴即可．【解答】解：（Ⅰ）若a=﹣2，则，x∈（0，+∞）由f'（x）＞0得，0＜x＜1；由f'（x）＜0得，x＞1．所以函数f（x）的单调增区间为（0，1）；单调减区间为（1，+∞）．（Ⅱ）依题意，在区间上f（x）min＞1.，a≥1．令f'（x）=0得，x=1或．若a≥e，则由f'（x）＞0得，1＜x≤e；由f'（x）＜0得，．所以f（x）min=f（1）=a﹣1＞1，满足条件；若1＜a＜e，则由f'（x）＞0得，或1＜x≤e；由f'（x）＜0得，.，依题意，即，所以2＜a＜e．若a=1，则f'（x）≥0．所以f（x）在区间上单调递增，，不满足条件；综上，a＞2．（III）x∈（0，+∞），g（x）=ax2﹣（a+1）xlnx+（a+1）x﹣1．所以g'（x）=2ax﹣（a+1）lnx．设m（x）=2ax﹣（a+1）lnx，．令m'（x）=0得．当时，m'（x）＜0；当时，m'（x）＞0．所以g'（x）在上单调递减，在上单调递增．所以g'（x）的最小值为．因为，所以．所以g'（x）的最小值．从而，g（x）在区间（0，+∞）上单调递增．又，设h（a）=e3a﹣（2lna+6）．则．令h'（a）=0得．由h'（a）＜0，得；由h'（a）＞0，得．所以h（a）在上单调递减，在上单调递增．所以．所以h（a）＞0恒成立．所以e3a＞2lna+6，．所以．又g（1）=2a＞0，所以当时，函数g（x）恰有1个零点．。