下载文档原格式
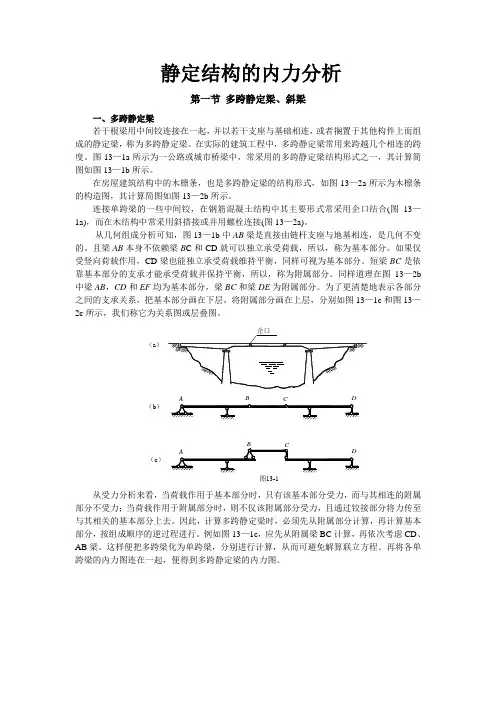
静定结构的内力分析第一节多跨静定梁、斜梁一、多跨静定梁若干根梁用中间铰连接在一起，并以若干支座与基础相连，或者搁置于其他构件上而组成的静定梁，称为多跨静定梁。
在实际的建筑工程中，多跨静定梁常用来跨越几个相连的跨度。
图13—1a所示为一公路或城市桥梁中，常采用的多跨静定梁结构形式之一，其计算简图如图13—1b所示。
在房屋建筑结构中的木檩条，也是多跨静定梁的结构形式，如图13—2a所示为木檩条的构造图，其计算简图如图13—2b所示。
连接单跨梁的一些中间铰，在钢筋混凝土结构中其主要形式常采用企口结合(图13—1a)，而在木结构中常采用斜搭接或并用螺栓连接(图13—2a)。
从几何组成分析可知，图13—1b中AB梁是直接由链杆支座与地基相连，是几何不变的。
且梁AB本身不依赖梁B C和CD就可以独立承受荷载，所以，称为基本部分。
如果仅受竖向荷载作用，CD梁也能独立承受荷载维持平衡，同样可视为基本部分。
短梁BC是依靠基本部分的支承才能承受荷载并保持平衡，所以，称为附属部分。
同样道理在图13—2b 中梁AB，CD和EF均为基本部分，梁BC和梁DE为附属部分。
为了更清楚地表示各部分之间的支承关系，把基本部分画在下层，将附属部分画在上层，分别如图13—1c和图13—跨梁的内力图连在一起，便得到多跨静定梁的内力图。
要依靠AC 梁才能保证其几何不变性，所以CE 梁为附属部分。
（2）计算支座反力从层叠图看出，应先从附属部分CE 开始取隔离体，如图13-3c 所示。
∑=0CM 04680=⨯-⨯D V kN V D 120=（↑） ∑=0DM04280=⨯-⨯C V kN V C 40=（↓）将C V 反向，作用于梁AC 上，计算基本部分∑=0X 0=AH∑=0AM －40×10+V B ×8+10×8×4-64=0 ∑=0BM－40×2－10×8×4－64+V A ×8=0V A =58kN （↑） V B =18kN （↓） 校核：由整体平衡条件得∑Y ＝—80十120—18十58—10×8＝0， 无误。
§3.6静定结构的内力分析和受力特点对静定结构来说，所能建立的独立的平衡方程的数目=方程中所含的未知力的数目。
因此，静定结构的内力完全由平衡条件确定。
为了避免解联立方程组应按一定的顺序截取单元（分离体），尽量使一个方程中只含一个未知量。
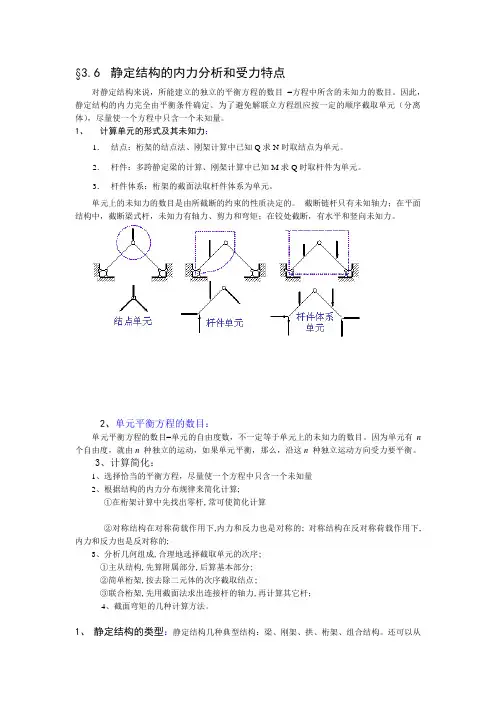
1、计算单元的形式及其未知力：1．结点：桁架的结点法、刚架计算中已知Q求N时取结点为单元。
2．杆件：多跨静定梁的计算、刚架计算中已知M求Q时取杆件为单元。
3．杆件体系：桁架的截面法取杆件体系为单元。
单元上的未知力的数目是由所截断的约束的性质决定的。
截断链杆只有未知轴力；在平面结构中，截断梁式杆，未知力有轴力、剪力和弯矩；在铰处截断，有水平和竖向未知力。
2、单元平衡方程的数目：单元平衡方程的数目=单元的自由度数，不一定等于单元上的未知力的数目。
因为单元有n 个自由度，就由n 种独立的运动，如果单元平衡，那么，沿这n 种独立运动方向受力要平衡。
3、计算简化：1、选择恰当的平衡方程，尽量使一个方程中只含一个未知量2、根据结构的内力分布规律来简化计算;①在桁架计算中先找出零杆,常可使简化计算②对称结构在对称荷载作用下,内力和反力也是对称的; 对称结构在反对称荷载作用下,内力和反力也是反对称的;3、分析几何组成,合理地选择截取单元的次序;①主从结构,先算附属部分,后算基本部分;②简单桁架,按去除二元体的次序截取结点;③联合桁架,先用截面法求出连接杆的轴力,再计算其它杆；4、截面弯矩的几种计算方法。
1、静定结构的类型：静定结构几种典型结构：梁、刚架、拱、桁架、组合结构。
还可以从不同的角度加以分类。
1、几种典型结构：梁、刚架、拱、桁架、组合结构。
2、减小截面弯矩的措施链杆只有轴力，无弯矩，截面上正应力均布，充分利用了材料的强度。
弯杆有弯矩，截面上正应力不均布，没有充分利用材料强度。
为达到物尽其用，尽量减小杆件中的弯矩。
减小截面弯矩的几种措施。
①在静定多跨梁中，利用杆端负弯矩可减小跨中正弯矩；②在推力结构中，利用水平推力可减小弯矩峰值；③在桁架中，利用杆件的铰结及荷载的结点传递，使各杆处于无弯矩状态；三铰拱采用合理拱轴线可处于无弯矩状态。
