偏角法测设圆曲线测设数据计算

圆曲线的详细测设学生姓名：郑妮娟学号：08300486专业班级：工程测量与监理384403 指导教师：张晓雅摘要本文阐述了在公路、铁路的路线圆曲线测设中，一般是在测设出曲线各主点后，随之在直圆点或圆直点进行圆曲线详细测设。

其中施工测量是整个施工进程和每一施工工序中的首要工作，其内容主要是建立平面控制网和高程系统，测定线路关键点，细部点的测设，中线（线路轴线），对圆曲线进行施工放样测量，并在施工进程中进行相关的测量等，以确保施工质量和施工过程的安全。

本文通过仪器安置不同地方进行多种圆曲线测设，提出了偏角法、切线支距法和全站仪法详细测设圆曲线的方法，对圆曲线上各点进行测设。

关键词：圆曲线、详细测设目录引言 (1)1.圆曲线测设的目的意义 (1)2. 圆曲线的主点测设 (2)2.1圆曲线要素计算 (2)2.2 主点里程计算 (3)2.3主点测设： (3)３.圆曲线的详细测设 (4)3.1 偏角法详细测设圆曲线 (4)3.2切线支距法详细测设圆曲线 (5)3.3全站仪法测设圆曲线 (7)5 圆曲线的详细测设案例： (9)结论 (11)致谢 (12)参考文献 (13)引言线路测量，包括公路、铁路、运河、供水明渠、输电线路、各种用途的管道工程等。

这些工程的主体一般是由直线和曲线构成，长度可能延伸十几公里以至几百公里，它们在勘测设计及施工测量方面有不少共性。

当线路由一个方向转到另一个方向时，必须用曲线来连接。

曲线的形式较多，其中，圆曲线（又称单曲线）是最常用的曲线形式。

圆曲线的测设一般分为两步进行：首先是圆曲线主点的测设，即圆曲线的起点（直圆点ZY）、中点（曲中点QZ）和终点（圆直点YZ）的测设；然后在各主点之间进行加密，按照规定桩距测设曲线的其他各桩点。

1.圆曲线测设的目的意义铁路和公路线路由于受地形、地质或其他原因的影响，经常要改变方向。

为了满足行车方便要求，需要在两直线段之间插入平面曲线把它们连接起来。

文献综述一、圆曲线的详细测设在各类线路工程弯道处施工，常常会遇到圆曲线的测设工作。

目前，圆曲线测设的方法已有多种，如偏角法、切线支距法、弦线支距法等。

然而，在实际工作中测设方法的选用要视现场条件、测设数据求算的繁简、测设工作量的大小，以及测设时仪器和工具情况等因素而定。

另外，上述的几种测设方法，都是先根据辅点的桩号（里程）来计算测设数据，然后再到实地放样。

因此，在实际工作中利用上述传统测设方法，有时会因地形条件的限制而无法放样出辅点（如不通视或量距不便等），或放样出的辅点处无法设置标桩。

在本次毕业设计的论文课题中介绍的几种圆曲线测设的新方法，不仅计算简单、测设便捷，而且可在不需要知道曲线上某点里程的情况下进行，从而避免了按预先给定的曲线点反算的测设数据放样不通视而转站的麻烦。

同时，利用本文介绍的新方法，还可以根据线路工程施工进度的要求，灵活地选择性地放样出部分曲线；也可以用于快速地确定曲线上某一加桩的位置；若用于线路验收测量，则更加方便，验测结果更具有代表性、更可靠。

二、全站仪在任意站测设圆曲线及方法交点偏角法测设方法用全站仪任意站测设圆曲线，安置一次仪器就能完成全部工作。

虽然外业计算麻烦，但对于不能设站的转点，可谓方便灵活。

但它的不足之处仍然是计算烦锁，对于不熟悉内业的外业工作者，很难实际操作。

如果利用一些程序计算器，编制输入：AB 的四组坐标和半径、九个数据的程序，可迅速得出放样数据，简化了外业工作。

为了放样工作的便利,可在平面控制网中纳入一些放样点,构成GPS同级全面网。

由于放样点间距离较近,在进行同步环和闭合环检验时可仅考虑各分量的较差,而不考虑相对闭合差。

因为,用相对闭合差来衡量是不合理的。

由于GPS接收机的固定误差,相位中心偏差以及观测时的对中误差均在1mm～5mm之间,对于几十米的短边,其相对闭合差值势必较大。

3)平面控制网的设计主要考虑独立基线的选择以及异步闭合环的设计,要考虑构成尽可能多的闭合图形,并将网中处于边缘的观测点用独立基线连接起来,形成封闭图形。

第三节圆曲线的详细测设§11 —3圆曲线的详细测设一、偏角法测设圆曲线圆曲线的主点ZY、QZ、YZ定出后,为在地面上标定出圆曲线的形状，还必须进行曲线的加密工作。

曲线点：对圆曲线进行加密，详细测设定出的曲线上的加密点。

曲线点的间距：一般规定，R> 150 m时曲线点的间距为20m, 50m W R<150m时曲线点的间距为10m 。

R<50m时曲线上每隔5m测设一个细部点；在点上要钉设木桩，在地形变化处还要钉加桩。

曲线测设：设置曲线点的工作，常用的方法有：偏角法和切线支距法。

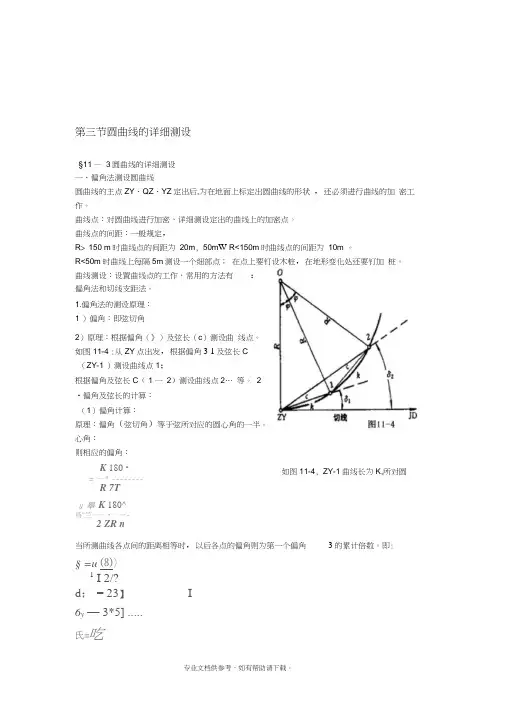
1.偏角法的测设原理：1 ）偏角：即弦切角2）原理：根据偏角（》）及弦长（c）测设曲线点。

如图11-4 :从ZY点出发，根据偏角3 1及弦长C（ZY-1 ）测设曲线点1；根据偏角及弦长C（ 1 一2）测设曲线点2… 等。

2•偏角及弦长的计算：（1）偏角计算：原理：偏角（弦切角）等于弦所对应的圆心角的一半。

心角：则相应的偏角：K 180 •如图11-4, ZY-1曲线长为K,所对圆= —* --------R 7Tu 舉K 180^爲"竺——•——-2 ZR n当所测曲线各点间的距离相等时，以后各点的偏角则为第一个偏角3的累计倍数。

即:§ =u ⑻)1I 2/?d； = 23】I6y—3*5] .....氏=吃（2）弦长计算（如图11-4）严密计算公式：Jrdi /f(' =2R sin $sin — =C二sin —1 2 R■※弦弧差（弦长与其相对应的曲线长之差）：弦弧差=K i -C i = L i3/（24R2）当R=450m时，20m的弦弧差为2mm ,•••当R>400m时，不考虑弦弧差的影响。

由于铁路曲线半径一般很大，20m的弦长与其相对应的曲线长之差很小，就用弦长代替相应的曲线长进行圆曲线测设。

近似计算：'、"整弦：里程为20m倍数的两相邻曲线点间的弦长（曲线点间距20m对应的弦长）。

第四章圆曲线要素计算及测设根据提供资料，=40º20′（右）,R=120米，转角点JD的桩号为K3+135.12，用偏角法测设各桩点（规定桩距为20米）。

切线长：曲线长:外矢距：切曲差：经计算，T=36.73 L=70.40 E=6.53根据JD的桩号为K3+135.12，则：JD桩号 K3+135.12-) T 36.73ZY桩号 K3+098.39+) L 70.40YZ桩号 K3+098.39-) L/2 35.20QZ桩号 K3+133.59+) D/2 1.53JD桩号 K3+135.12所以，经计算交点的里程与校核计算相符。

第一节仪器安置在ZY点上的施测法一、在ZY点上施测法11．计算根据转折角和半径R及交点桩计算三主点的桩号为：ZY： K3+098.39； QZ ：K3+133.59 ；YZ： K3+168.79。

因ZY点的里程为3+098.39，在曲线上，它前面最近的整里程为3+100.00，所以起始弧长=（3+100）-（3+098.39）=1.61（m）。

又因点YZ点的里程为3+168.79，在曲线上，它后面最近的里程为3+160.00，弧长=(3+168.79)-(3+160.00)=8.79（m）。

现将计算的偏角值到列表如表4-1，供测设时使用。

为检查计算有无错误，可与总偏角核对。

本次研究课题中的总偏角为=20º10′00″，与计算之总偏角20º10′05″相差05″，这是因为偏角表计算至秒为止，秒后数值四舍五入所造成的误差，与测量精度无影响，属容许误差。

2、施测方法：如图4-1所示，将仪器安置在ZY点上，全站仪显示对准0º0′0″，后视JD，然后旋转望远镜，拨至第一桩点K3+100.00的偏角0º27′40″，从ZY点起沿此方向量出第一段曲线长 1.61米相应的弦长，定出第一桩点。

再拨至第二桩点K3+120.00的偏角6º11′26″，从第一桩点量出第二段曲线长20米相应的弦长，交出第二桩点。

1、圆曲线计算公式：切线长 T=R*tan 2a 曲线长 L=R*180πa 外矢距 E 0=R(sec 2a -1)=R(1/cos 2a -1) 2、偏角法测设圆曲线：偏角计算： δ=2ϕ=RKπ90 式中，R 为曲线半径；K 为置镜点至测设点的曲线长。

若测设点间曲线长相等，设第1点偏角为δ1，则各点偏角依次为： δ2=2*δ1 δ3=3*δ 1 δn =n*δ13、长弦偏角法测设圆曲线：利用光电测距仪配合有编程功能的计算器来测设曲线，采用长弦偏角法最适宜。

δi =2ϕ=RKπ90 c i =2 R sin δ0式中K 为测设的曲线长，δi 、c i 为测设曲线点i 的偏角与弦长。

1、缓和曲线方程式 x =l -22540l R ly =036l R l当l =l 0时（l 0为缓和曲线总长度），则x =x 0 y =y 0xo =l o -2340R l y o=Rl622、缓和曲线常数的计算β0=πR l 090δ0=31βm =20l -230240Rlp ≈Rl2423、曲线综合要素计算： 切线长 T =m +（R +p ）* tan 2a曲线长 L =l o +180απR 外矢距 E 0=2cosαPR +-R切曲差 q =2T-Lx4、偏角计算：缓和曲线上任一点i 的偏角为：β=0290l R l πδ=31βb =β-δ=2δ 同理可得 b 0=2δ0δ为缓和曲线上任一点的正偏角，b 为该点的反偏角。

缓和曲线上任一点后视起点的反偏角，等于由起点测设该点正偏角的二倍。

设δ1为第一点的偏角，δi 为第i 点的偏角，则，δi =026l R l i π*π180偏角与测点到缓和曲线起点的曲线长度的平方成正比。

δ1=2Nlδ0由缓和曲线的总偏角δ0，可求得缓和曲线上任一点的偏角δi 。

置镜于ZH （HZδi =026l R l i π*π180b i =2δiβi =3δiZH。

交点偏角法测设圆曲线在公路、铁路的路线圆曲线测设中，一般是在测设出曲线各主点后，随之在直圆点或圆直点进行圆曲线详细测设。

其测设的方法很多，诸如偏角法、切线支距法、弦线支距法、延弦法等。

这些方法有一个共同点：均是在定测阶段放样出的线路交点处设站，以路线后视方向定向，在实地定出曲线主点，然后将仪器置于曲线主点(一般是在曲线起点)处，以路线交点为后视方向定向，进行圆曲线详细测设。

这些方法在实际施测过程中，由于各种地形条件的限制以及施测方法的特点，可能会出现以下三种情况：(1)在曲线主点处无法设站。

(2)后视方向太近，定向不准。

(3)误差积累较大。

为此，在交点可以设站的情况下，可以采用一种新的测设方法—交点偏角法。

1 线路的转向一般由圆曲线和缓和曲线完成，下面分两种情况介绍图11.1 在圆曲线与两直线段间加设了两段缓和曲线，线路的转向由三段曲线完成如图1所示：ZH(A)为直缓点、HY(B)为缓圆点、YH(C)为圆缓点、HZ(E)为缓直点、QZ(F)为曲中点，它们称为曲线主点；E为外矢距；JD(D)为线路交点；α为线路转角；R为圆曲线半径；O为圆曲线圆心；L为圆曲线上某待测设点i至QZ(F)点间的弧长。

计算公式推导如下：由图1所表示的几何关系，可得出iF所对的圆心角Φ及iF弦长：Φ=180°L/(πR)(1)iF=2Rsin(Φ/2)(2)=2Rsin[90°L/(πR)](3)∵在ΔiOF中，iO=FO (4)∴κ=λ (5)∴λ=180°-Φ/2=90°-90°L/(πR)(6)∴Ψ=180°-λ=90°+90°L/(πR)(7)又根据余弦定理得：Di=(E2+iF2-2E×iF×cosΨ)1/2(8)将(3)、(7)式带入(8)式并化简得：Di=E2+4Rsin2[90°L/(πR)(R+E)](9)又根据正弦定理得：γ=arcsin[iF×sinΨ/(iD)] (10)将(3)、(7)、(9)式带入(10)并化简得：γ=arcsin{R×sin[180°L/(πR)]/Di}(11)∴β=(90°-α2)-γ=(90°-α/2)- arcsin{R×sin[180°L/(πR)]/Di}(12)其中：E=(R+p)sec(α/2)-R(p=L02/(24R)，为因加设缓和曲线圆曲线相对于切线的内移量；L0为缓和曲线长度)。

铁路曲线要素的测设、计算与精度分析1-1 圆曲线的测设铁路线路平面曲线分为两种类型：一种是圆曲线，主要用于专用线和行车速度不高的线路上；另一种是带有缓和曲c线的圆曲线，铁路干线上均用此种曲线。

铁路曲线测设一般分两步进行，先测设曲线主点，然后依据主点详细测设曲线。

铁路曲线测设常用的方法有：偏角法、切线支距法和极坐标法。

圆曲线（圆曲线段长度）（circular curve）线路平面方向改变时，在转向处所设置的曲率不变的曲线。

圆曲线线型由一个圆曲线组成的曲线称为单曲线；由两个或两个以上同向圆曲线组成的称为复曲线。

转向相同的两相邻曲线连同其间的直线段所组成的曲线称为同向曲线；转向相反的两相邻曲线连同其间的直线段所组成的曲线称为反向曲线。

圆曲线铁路由于复曲线会增加勘测设计、施工和养护维修的困难，降低列车运行的平稳性和旅客舒适条件，因此新建铁路一般不应设置复曲线；在困难条件下，为减少改建工程，改建既有线可保留复曲线；增建与之并行的第二线，如有充分的技术经济依据，也可采用复曲线圆曲线长度在圆曲线地段，为了克服列车在曲线上运行而产生的离心力，需设置外轨超高（参见曲线超高），当曲线半径较小时，为保证列车按强制自由内接形式通过曲线，需进行必要的轨距加宽；为了平顺地过渡曲线率、外轨超高和轨距加宽，保证行车平稳与旅客舒适，在圆曲线的两端需设置一定长度的缓和曲线；同时圆曲线的最小长度受、曲线测设、养护维修、行车平稳和旅客舒适等条件控制，因确定圆曲线和夹直线长度的理论与计算方法在力学上无大的差别，故圆曲线最小长度与夹直线最小长度采用同一标准。

圆曲线要素曲线偏角的大小影响列车在曲线上的运行阻力。

曲线半径、外轨超高、缓和曲线长度和圆曲线长度对行车速度起限制作用（参见曲线限速），因此，这此要素要根据行车速度拟定。

曲线偏角（转向角）、曲线半径R、缓和曲线长度lo、切线长度T和曲线长度L统称为曲线要素。

这些要素的确定及各曲线主点里程的推算是曲线设计的主要内容。

顶岗实习报告道路工程测量(圆曲线缓和曲线计算公式) 实习时间：2013年7月至2013年9月17日 工程项目名称：乌鲁木齐绕城高速公路（东线）WRDX-3实习报告内容：经过实习的一段时间发现道路测量与建筑测量之间有很大的差别，道路测量主要就是曲线上放样，而建筑测量中为直线直角放样。

因此道路测量人员必须掌握曲线放样的内容。

而曲线放样的内容主要就是圆曲线和缓和曲线，一般采用的方法就是交点放样法和偏角法下面就是我在这一段时间内学习到的关于曲线放样的基本内容。

重点：圆曲线、缓和曲线的要素计算和主点测设方法；切线支距法和偏角法的计算公式和测设方法；路线纵断面的基平、中平测量和横断面测量方法 难点：缓和曲线的要素计算和主点测设方法；缓和曲线的切线支距法和偏角法的计算公式和测设方法。

交点转点转角及里程桩的测设一、 道路工程测量概述分为：路线勘测设计测量 (route reconnaissance and design survey) 和道路施工测量 (road construction survey) 。

（一） 勘测设计测量 (route reconnaissance and design survey) 分为：初测 (preliminary survey) 和定测 (location survey) 1、 初测内容：控制测量 (control survey) 、测带状地形图 (topographical map of a zone)和纵断面图 (profile) 、收集沿线地质水文资料、作纸上定线或现场定线，编制比较方案，为初步设计提供依据。

2、 2、定测内容：在选定设计方案的路线上进行路线中线测量 (center line survey) 、测纵断面图 (profile) 、横断面图 (cross-section profile) 及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查，为施工图设计提供资料。

一、圆曲线1、圆曲线计算公式：切线长 T=R*tan曲线长 L=R*外矢距 E0=R(sec-1=R(1/cos-12、偏角法测设圆曲线：偏角计算：δ==式中，R为曲线半径；K为置镜点至测设点的曲线长。

若测设点间曲线长相等，设第1点偏角为δ1，则各点偏角依次为：δ2=2*δ1 δ3=3*δ1 δn=n*δ13、长弦偏角法测设圆曲线：利用光电测距仪配合有编程功能的计算器来测设曲线，采用长弦偏角法最适宜。

δi== c i=2 R sinδ0式中K为测设的曲线长，δi、c i为测设曲线点i的偏角与弦长。

二、缓和曲线y1、缓和曲线方程式lx=l-PyZHxy=式中，x、y为缓和曲线上任一点的直角坐标，坐标原点为直缓点（ZH）或缓直点（HZ）；通过该点的缓和曲线切线为x轴。

l为缓和曲线上任一点P到ZH（或HZ）的曲线长。

x当l=l0时（l0为缓和曲线总长度），则x=x0y=y0式中，xo、yo为缓圆点（HY）或圆缓点（YH）的坐标x o=l o-y o=2、缓和曲线常数的计算βo—缓和曲线的切线角；δ0—缓和曲线的总偏角；m—切垂距；p—圆曲线内移量。

β0=δ0=β0m=-p≈3、曲线综合要素计算：切线长T=m+（R+p）* tan曲线长L=l o+外矢距E0=-R切曲差q=2T-L4、偏角计算：缓和曲线上任一点i的偏角为：β=δ=βb=β-δ=2δ同理可得b0=2δ0δ为缓和曲线上任一点的正偏角，b为该点的反偏角。

缓和曲线上任一点后视起点的反偏角，等于由起点测设该点正偏角的二倍。

设δ1为第一点的偏角，δi为第i点的偏角，则，δi=*偏角与测点到缓和曲线起点的曲线长度的平方成正比。

δ1=δ0由缓和曲线的总偏角δ0，可求得缓和曲线上任一点的偏角δi。

置镜于ZH（HZ）测设缓和曲线上任意点的偏角l0liHYδi=*βiiβb i=2δiZHβi=3δi。

实验一圆曲线测设一、目的和要求（1）掌握圆曲线主点元素的计算和主点的测设方法。

（2）掌握用偏角法进行圆曲线的详细测设二、计划和设备（1）试验时数安排为4学时，实验小组由5人组成（2）实验设备为DJ6经纬仪1台，钢尺1把，标杆2支，测钎10支，木桩3支，榔头1把，记录板1块，计算器1支。

三、方法和步骤1.圆曲线主点测设道路圆曲线主点测设之前，需要有标定路线方向的交点(JD)和转点（ZD）。

在空旷地面打一木桩作为路线交点JD1，然后向两个方向（路线的转折角约等于）延伸30 m以上，定出两个转点ZD1和ZD2，插上测钎。

如图1-1所示。

图1-1 圆曲线的主点测设元素在JD1点安置经纬仪，以一个测回测定转折角，计算路线偏角。

设计圆曲线的半径，按下列公式计算圆曲线元素（切线长T、曲线长L、外距E、切曲差q，记录于附录表2中。

用安置于JD1点的经纬仪先后瞄准ZD1，ZD2定出方向，用钢尺在该方向上测设且切线长T，定出圆曲线的起点（直圆点）ZY和圆曲线的终点（圆直点）YZ，打下木桩，重新测设一次，在木桩顶上标出ZY 和YZ的精确位置。

用经纬仪瞄准YZ，水平读盘读数置于，照准部旋转，定出转折角的分角线方向，用钢尺测设外距E，定出圆曲线中点QZ 。

1.主点桩号计算位于道路中线上的曲线主点桩号由交点的桩号推算而得。

设交点JD1的桩号为，根据圆曲线元素，计算曲线主点的桩号：（检核）1.用偏角法详细测设圆曲线设圆曲线上里程每整需要测设里程桩，则，为曲线上第一个整桩与圆曲线起点ZY间的弧长，如图1-2所示。

图1-2 用偏角法详细测设圆曲线用偏角法详细测设圆曲线，按下式计算测设点的偏角和以后每增加弧长的各点的偏角增量：等细部点的偏角按下式计算：……曲线起点至曲线上任一细部点的弦长按下式计算：曲线上相邻整桩间的弦长按下式计算：曲线上任两点间的弧长与弦长之差（弦弧差）按下式计算：根据以上这些公式和算得的曲线主点桩号，计算圆曲线偏角法测设数据，记录于附录表2中。