晶格振动与晶体的热学性质-习题【范本模板】

第三章 晶格振动与晶体的热学性质1。

什么是简谐近似？解:当原子在平衡位置附近作微小振动时，原子间的相互作用可以视为与位移成正比的虎克力，由此得出原子在其平衡位置附近做简谐振动。

这个近似即称为简谐近似。

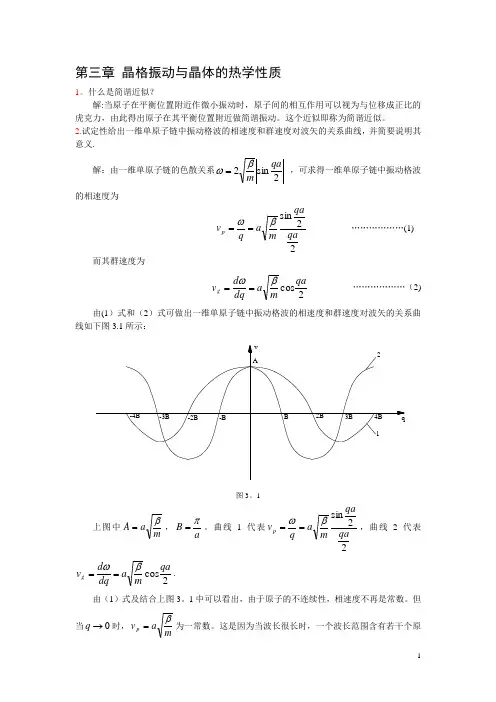
2.试定性给出一维单原子链中振动格波的相速度和群速度对波矢的关系曲线，并简要说明其意义.解：由一维单原子链的色散关系2sin2qamβω= ，可求得一维单原子链中振动格波的相速度为22sinqa qamaqv p βω== (1)2cos qam a dq d v g βω==. 由（1）式及结合上图3。

1中可以看出，由于原子的不连续性，相速度不再是常数。

但当0→q 时，mav p β=为一常数。

这是因为当波长很长时，一个波长范围含有若干个原子，相邻原子的位相差很小，原子的不连续效应很小，格波接近与连续媒质中的弹性波。

由（2）式及结合上图3。

1中可以看出，格波的群速度也不等于相速度.但当0→q ，mav v p g β==，体现出弹性波的特征，当q 处于第一布区边界上，即aq π=时，0=g v ,而mav p βπ2=，这表明波矢位于第一布里渊区边界上的格波不能在晶体中传播，实际上它是一种驻波。

3。

周期性边界条件的物理含义是什么？引入这个条件后导致什么结果?如果晶体是无限大,q 的取值将会怎样？解：由于实际晶体的大小总是有限的,总存在边界，而显然边界上原子所处的环境与体内原子的不同，从而造成边界处原子的振动状态应该和内部原子有所差别。

考虑到边界对内部原子振动状态的影响,波恩和卡门引入了周期性边界条件.其具体含义是设想在一长为Na 的有限晶体边界之外，仍然有无穷多个相同的晶体，并且各块晶体内相对应的原子的运动情况一样，即第j 个原子和第j tN +个原子的运动情况一样，其中t ＝1,2，3…。

引入这个条件后，导致描写晶格振动状态的波矢q 只能取一些分立的不同值。

如果晶体是无限大,波矢q 的取值将趋于连续。

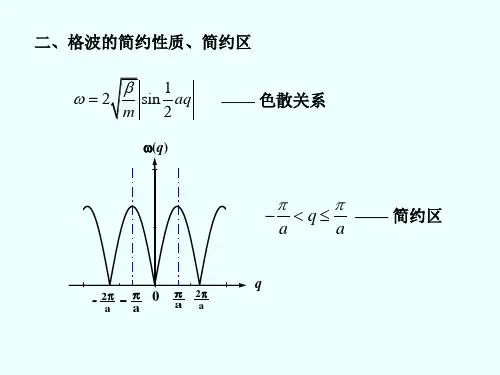
固体物理第三章班级成绩学号Chapter 3 晶格振动与晶体的热学性质姓名(lattice vibration and its heat characteristics)⼀、简要回答下列问题(answer the following questions):1、在晶格常数为a 的⼀维单原⼦晶格中，波长λ=8a 和波长λ=8a/5的格波所对应的原⼦振动状态有⽆不同? 试画图加以说明。

［答］对于⼀维单原⼦链，由q=2π／λ知，λ＝8a 时，q ＝π／4a ，λ＝8a ／5时，q ＝5π／4a ，⼆者的aq 相差π，不是2π的整数倍，因此，两个格波所对应的原⼦振动状态不同。

如上图，当两个格波的位相差为2π的整数倍时，则它们所对应的原⼦的振动状态相同。

2、什么叫简正振动模式？简正振动数⽬、格波数⽬或格波振动模式数⽬是否是⼀回事？［答］在简谐振动下，由N 个原⼦构成的晶体的晶格振动，可等效成3N 个独⽴的谐振⼦的振动，每⼀个谐振⼦的振动模式称为简正振动模式。

格波振动通常是这3N 个简正振动模式的线性叠加。

简正振动数⽬、格波数⽬或格波振动模式数⽬是是⼀回事，其数⽬等于晶体中所有原⼦的⾃由度之和，即等于3N 。

3、晶体中声⼦数⽬是否守恒？在极低温下，晶体中的声⼦数与温度T 之间有什么样的关系？［答］频率为ωi 的格波的平均声⼦数为： 11)(/-=Tk i B en ωω即每⼀个格波的声⼦数都与温度有关，因此晶体中的声⼦数⽬不守恒，它随温度的改变⽽改变。

以德拜模型为例。

晶体中的声⼦数⽬为ωωωωd g n N D)()('0=其中令 T k x B ω= 则 123'2/033233-=x TB e dxx C T k V N D θπ在极低温度下，θD ／T →∞，于是 331332332033233)2(23123'T nC T Vk e dx x C T k V N n B x B ∑∞=∞=-=ππ即在温度极低时，晶体中的声⼦数⽬与T 3成正⽐。

第三章晶格振动与晶体热学性质习题解答1. 相距为不是晶格常数倍数的两个同种原子, 其最大振幅是否相同?[解答]以同种原子构成的一维双原子分子链为例, 相距为不是晶格常数倍数的两个同种原子, 设一个原子的振幅A, 另一个原子振幅B, 由本教科书的(3.16)可得两原子振幅之比(1)其中m原子的质量. 由本教科书的(3.20)和(3.21)两式可得声学波和光学波的频率分别为, (2). (3)将(2)(3)两式分别代入(1)式, 得声学波和光学波的振幅之比分别为, (4). (5)由于=，则由(4)(5)两式可得, . 即对于同种原子构成的一维双原子分子链, 相距为不是晶格常数倍数的两个原子, 不论是声学波还是光学波, 其最大振幅是相同的.2. 引入玻恩卡门条件的理由是什么?[解答](1)(1)方便于求解原子运动方程.由本教科书的(3.4)式可知, 除了原子链两端的两个原子外, 其它任一个原子的运动都与相邻的两个原子的运动相关. 即除了原子链两端的两个原子外, 其它原子的运动方程构成了个联立方程组. 但原子链两端的两个原子只有一个相邻原子, 其运动方程仅与一个相邻原子的运动相关, 运动方程与其它原子的运动方程迥然不同. 与其它原子的运动方程不同的这两个方程, 给整个联立方程组的求解带来了很大的困难.(2)(2)与实验结果吻合得较好.对于原子的自由运动, 边界上的原子与其它原子一样, 无时无刻不在运动. 对于有N个原子构成的的原子链, 硬性假定的边界条件是不符合事实的. 其实不论什么边界条件都与事实不符. 但为了求解近似解, 必须选取一个边界条件. 晶格振动谱的实验测定是对晶格振动理论的最有力验证(参见本教科书§3.2与§3.4). 玻恩卡门条件是晶格振动理论的前提条件. 实验测得的振动谱与理论相符的事实说明, 玻恩卡门周期性边界条件是目前较好的一个边界条件.3.什么叫简正振动模式？简正振动数目、格波数目或格波振动模式数目是否是一回事？[解答]为了使问题既简化又能抓住主要矛盾，在分析讨论晶格振动时，将原子间互作用力的泰勒级数中的非线形项忽略掉的近似称为简谐近似. 在简谐近似下, 由N 个原子构成的晶体的晶格振动, 可等效成3N个独立的谐振子的振动. 每个谐振子的振动模式称为简正振动模式, 它对应着所有的原子都以该模式的频率做振动, 它是晶格振动模式中最简单最基本的振动方式. 原子的振动, 或者说格波振动通常是这3N个简正振动模式的线形迭加.简正振动数目、格波数目或格波振动模式数目是一回事, 这个数目等于晶体中所有原子的自由度数之和, 即等于3N.4.长光学支格波与长声学支格波本质上有何差别?[解答]长光学支格波的特征是每个原胞内的不同原子做相对振动, 振动频率较高, 它包含了晶格振动频率最高的振动模式. 长声学支格波的特征是原胞内的不同原子没有相对位移, 原胞做整体运动, 振动频率较低, 它包含了晶格振动频率最低的振动模式, 波速是一常数. 任何晶体都存在声学支格波, 但简单晶格(非复式格子)晶体不存在光学支格波.5. 晶体中声子数目是否守恒?[解答]频率为的格波的(平均) 声子数为,即每一个格波的声子数都与温度有关, 因此, 晶体中声子数目不守恒, 它是温度的变量.按照德拜模型, 晶体中的声子数目N’为.作变量代换，.其中是德拜温度. 高温时,,即高温时, 晶体中的声子数目与温度成正比.低温时, ,,即低温时, 晶体中的声子数目与T 3成正比.6.温度一定，一个光学波的声子数目多呢, 还是声学波的声子数目多?[解答]频率为的格波的(平均) 声子数为.因为光学波的频率比声学波的频率高, ()大于(), 所以在温度一定情况下, 一个光学波的声子数目少于一个声学波的声子数目.7.对同一个振动模式, 温度高时的声子数目多呢, 还是温度低时的声子数目多?[解答]设温度T H>T L, 由于()小于(), 所以温度高时的声子数目多于温度低时的声子数目.8.高温时, 频率为的格波的声子数目与温度有何关系?[解答]温度很高时, , 频率为的格波的(平均) 声子数为.可见高温时, 格波的声子数目与温度近似成正比.9. 从图3.6所示实验曲线, 你能否判断哪一支格波的模式密度大? 是光学纵波呢, 还是声学纵波?[解答]从图3.6所示实验曲线可以看出, 在波矢空间内, 光学纵波振动谱线平缓, 声学纵波振动谱线较陡. 单位频率区间内光学纵波对应的波矢空间大, 声学纵波对应的波矢空间小. 格波数目与波矢空间成正比, 所以单位频率区间内光学纵波的格波数目大. 而模式密度是单位频率区间内的格波数目, 因此光学纵波的模式密度大于声学纵波的模式密度.10.喇曼散射方法中，光子会不会产生倒逆散射？[解答]晶格振动谱的测定中, 光波的波长与格波的波长越接近, 光波与声波的相互作用才越显著. 喇曼散射中所用的红外光，对晶格振动谱来说, 该波长属于长波长范围. 因此, 喇曼散射是光子与长光学波声子的相互作用. 长光学波声子的波矢很小, 相应的动量不大. 而能产生倒逆散射的条件是光的入射波矢与散射波矢要大, 散射角也要大. 与大要求波长小, 散射角大要求大(参见下图), . 但对喇曼散射来说, 这两点都不满足. 即喇曼散射中，光子不会产生倒逆散射.11.长声学格波能否导致离子晶体的宏观极化?[解答]长光学格波所以能导致离子晶体的宏观极化, 其根源是长光学格波使得原胞内不同的原子(正负离子)产生了相对位移. 长声学格波的特点是, 原胞内所有的原子没有相对位移. 因此, 长声学格波不能导致离子晶体的宏观极化.12.金刚石中的长光学纵波频率与同波矢的长光学格横波频率是否相等? 对KCl晶体, 结论又是什么?[解答]长光学纵波引起离子晶体中正负离子的相对位移, 离子的相对位移产生出宏观极化电场, 电场的方向是阻滞离子的位移, 使得有效恢复力系数变大, 对应的格波的频率变高. 长光学格横波不引起离子的位移, 不产生极化电场, 格波的频率不变. 金刚石不是离子晶体, 其长光学纵波频率与同波矢的长光学格横波频率相等. 而KCl晶体是离子晶体, 它的长光学纵波频率与同波矢的长光学格横波频率不相等, 长光学纵波频率大于同波矢的长光学格横波频率.13.何谓极化声子? 何谓电磁声子?[解答]长光学纵波引起离子晶体中正负离子的相对位移, 离子的相对位移产生出宏观极化电场, 称长光学纵波声子为极化声子.由本教科书的(3.103)式可知, 长光学横波与电磁场相耦合, 使得它具有电磁性质, 人们称长光学横波声子为电磁声子.14.你认为简单晶格存在强烈的红外吸收吗？[解答]实验已经证实, 离子晶体能强烈吸收远红外光波. 这种现象产生的根源是离子晶体中的长光学横波能与远红外电磁场发生强烈耦合. 简单晶格中不存在光学波, 所以简单晶格不会吸收远红外光波.15.对于光学横波, 对应什么物理图象?[解答]格波的频率与成正比. 说明该光学横波对应的恢复力系数.时, 恢复力消失, 发生了位移的离子再也回不到原来的平衡位置, 而到达另一平衡位置, 即离子晶体结构发生了改变(称为相变). 在这一新的结构中, 正负离子存在固定的位移偶极矩, 即产生了自发极化, 产生了一个稳定的极化电场.16. 爱因斯坦模型在低温下与实验存在偏差的根源是什么?[解答]按照爱因斯坦温度的定义, 爱因斯坦模型的格波的频率大约为, 属于光学支频率. 但光学格波在低温时对热容的贡献非常小, 低温下对热容贡献大的主要是长声学格波. 也就是说爱因斯坦没考虑声学波对热容的贡献是爱因斯坦模型在低温下与实验存在偏差的根源.17.在甚低温下, 不考虑光学波对热容的贡献合理吗?[解答]参考本教科书（3.119）式, 可得到光学波对热容贡献的表达式.在甚低温下, 对于光学波, , 上式简化为.以上两式中是光学波的模式密度, 在简谐近似下, 它与温度无关. 在甚低温下, , 即光学波对热容的贡献可以忽略. 也就是说, 在甚低温下, 不考虑光学波对热容的贡献是合理的.从声子能量来说, 光学波声子的能量很大(大于短声学波声子的能量), 它对应振幅很大的格波的振动, 这种振动只有温度很高时才能得到激发. 因此, 在甚低温下, 晶体中不存在光学波.18.在甚低温下, 德拜模型为什么与实验相符?[解答]在甚低温下, 不仅光学波得不到激发, 而且声子能量较大的短声学格波也未被激发, 得到激发的只是声子能量较小的长声学格波. 长声学格波即弹性波. 德拜模型只考虑弹性波对热容的贡献. 因此, 在甚低温下, 德拜模型与事实相符, 自然与实验相符.19.在绝对零度时还有格波存在吗? 若存在, 格波间还有能量交换吗?[解答]频率为的格波的振动能为,其中是由个声子携带的热振动能, ()是零点振动能, 声子数.绝对零度时, =0. 频率为的格波的振动能只剩下零点振动能.格波间交换能量是靠声子的碰撞实现的. 绝对零度时, 声子消失, 格波间不再交换能量.20.温度很低时, 声子的自由程很大, 当时, , 问时, 对于无限长的晶体, 是否成为热超导材料?[解答]对于电绝缘体, 热传导的载流子是声子. 当时, 声子数n. 因此,时, 不论晶体是长还是短, 都自动成为热绝缘材料.21.石英晶体的热膨胀系数很小, 问它的格林爱森常数有何特点?[解答]由本教科书(3.158)式可知, 热膨胀系数与格林爱森常数成正比. 石英晶体的热膨胀系数很小, 它的格林爱森常数也很小. 格林爱森常数大小可作为晶格非简谐效应大小的尺度. 石英晶体的格林爱森常数很小, 说明它的非简谐效应很小.。

固体物理学答案朱建国版3HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】固体物理学·习题指导配合《固体物理学（朱建国等编着）》使用2022年4月28日第1章晶体结构 0第2章晶体的结合 (11)第3章晶格振动和晶体的热学性质 (17)第4章晶体缺陷 (26)第5章金属电子论 (30)第1章 晶体结构1.1 有许多金属即可形成体心立方结构，也可以形成面心立方结构。

从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略，并以R f 和R b 代表面心立方和体心立方结构中最近邻原子间的距离，试问R f /R b 等于 多少？答：由题意已知，面心、体心立方结构同一棱边相邻原子的距离相等，都设为a ：对于面心立方，处于 面心的原子与顶角原子的距离为：R f =2a对于体心立方，处于体心的原子与顶角原子的距离为：R b那么，RfRb =31.2 晶面指数为（123）的晶面ABC 是离原点O 最近的晶面，OA 、OB 和OC 分别与基失a 1，a 2和a 3重合，除O 点外，OA ，OB 和OC 上是否有格点若ABC 面的指数为（234），情况又如何答：晶面族（123）截a 1,a 2,a 3分别为1,2,3等份，ABC 面是离原点O 最近的晶面，OA 的长度等于a 1的长度，OB 的长度等于a 2长度的1/2，OC 的长度等于a 3长度的1/3，所以只有A 点是格点。

若ABC 面的指数为（234）的晶面族，则A 、B 和C 都不是格点。

1.3 二维布拉维点阵只有5种，试列举并画图表示之。

答：二维布拉维点阵只有五种类型，两晶轴b a 、，夹角 ，如下表所示。

1 简单斜方2 简单正方3 简单六角4 简单长方5 有心长方二维布拉维点阵1.4 在六方晶系中，晶面常用4个指数（hkil ）来表示，如图所示，前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a 1，a 2，a 3上的截距a 1/h ，a 2/k ，a 3/i ，第四个指数表示该晶面的六重轴c 上的截距c/l.证明：i=-（h+k ） 并将下列用（hkl ）表示的晶面改用（hkil ）表示：（001）(133)(110)(323)（100）（010）(213) 答：证明设晶面族（hkil ）的晶面间距为d ，晶面法线方向的单位矢量为n °。

第三章 晶格振动与晶体热学性质1． 原子质量为m,间距为a,恢复力常数为的一维简单晶格，频率为ω的格波)cos(qna t A u n -=ω，求（1） 该波的总能量，（2） 每个原子的时间平均总能量。

[解答]（1） 格波的总能量为各原子能量的总和。

其中第n 个原子的动能为,)(212tu m n ∂∂ 而该原子与第n+1个原子之间的势能为21)(21--n n u u β 若只为考虑最近邻相互作用，则格波的总能量为,)(1)(1212--+∂∂=∑∑n n nn n u u t um E β将)cos(pna t A u n-=ω代入上式得,2sin ])12(21[sin 421)(sin22222221qaqa n t A qna t A m E ⋅+-+-=∑∑ωβωϖϖ 设T 为原子振动周期，利用21)(sin 102=-⎰dt t TTϕω 可得()dtqa n t T A dt qna t T A qa T nT n 2221022210222sin ]12([sin 14)(sin 121⋅+-+-=E ⎰∑⎰∑ωβωω =241ωm A 2N +2sin 22qa N Aβ.式中N 为原子总数。

（2） 每个原子的时间平均总能量为2sin A A 412222qam N E βω+=-再利用色散关系2sin 4)cos 1(222qa m qa m ββϖ=-= 便得到每个原子的时间平均能量2221A m N E ϖ=-2． 一维复式格子，原子质量都为m ，原子统一编号，任一原子与两最近邻的间距不同,力常数不同,分别为1β和2β，晶格常数为a,求原子的运动方程及色散关系. [解答]图3.2 一维双原子分子链此题实际是一双原子分子链.设相邻分子间两原子的力常数为2β，间距为b ;一个分子内两原子力常数1β;晶格常数为a;第n-1,n,n+1,n+2个原子的位移分别为211,,,++-n n n n u u u u .第n-1与第n+1个原子属于同一原子,第n 与n+1第个原子属于同一个原子,于是第n 和第n+1个原子受的力分别为)()(1112-+---=n n n n n u u u u f ββ， )()(121211n n n n n u u u u f ---=++++ββ.其运动方程分别为)()(111222-+---=n n n n nu u u u dt u d m ββ )()(12121212n n n n n u u u u dtu d m ---=++++ββ 设格波的解分别为[][]t qna i t a q i n AeAeu n ϖϖ--==212)([][]t qna i t qb a q i n BeAeB u n ϖϖ--++==212)('1.代入运动方程，得 )()(122iqa Be A A B A m ----=-ββϖ .)()(212A B B Ae B m iqa---=-ββϖ整理得)()(,0)()(22122221=-++-=--+-B m A e B e A m iqaiqa ϖββββββϖββ由于A 和B 不可能同时为零。

第三章 晶格动力学和晶体的热学性质1.在同类原子组成的一维点阵中，若假设每个原子所受的作用力左右不同，其力常数如下图所示相间变化，且1β＞2β。

试证明：在这样的系统中，格波仍存在着声频支和光频支，其格波频率为解： 分析：此题实际是一个一维双原子链色散问题，设相邻分子间两原子的力常数为2β，间距为b ；一个分子内两原子力常数为1β，且1β＞2β；晶格常数为a ；质量为M 的原子位于n-1，n+1，n+3 ……，质量为m 的原子位于n ，n+2，n+4 ……，m=M ；第211,,,2,1,,1++-++-n n n n u u u u n n n n 个原子的位移分别为；第n-1与第n+1个原子属于同一原子，第n 与第n+2个原子属于同一原子，于是第n 个原子与第n+1个原子受得力分别是)()(1112-+---=n n n n n u u u u f ββ )()(121211n n n n n u u u u f ---=++++ββ相应的牛顿运动方程为 )()(111222-+---=n n n n nu u u u dt u d m ββ )()(12121212n n n n n u u u u dtu d m ---=++++ββ体系有N 个原胞，有2N 个独立的方程，上述方程的格波解为)2(t a nq i n Aeu ω-=B eB u t qb a nq i n ='=-++)2(1ω)2(t a nq i eω-将解代入方程得)()(122iqa Be A A B A m ----=-ββω)()(122B Ae A B B m iqa ----=-ββω整理得0)()(12221=+--+-B e A m iqa ββωββ0)()(12221=+--+-A e B m iqa ββωββ由于A 和B 不可能同时为0，因此其系数行列式必定为0即)()12221iqae m ββωββ+--+（)()(22112ωββββM e i q a -++--=0解上式得⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+-±+=2122121222212)2(sin )(16422)(qa m m m m ββββββω化简 ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+-±+=2122121212)2(sin )(411)(qa m ββββββω存在两种不同的格波的色散关系⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+--+=2122121212)2(sin )(411)(qa m A ββββββω ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+-++=2122121212)2(sin )(411)(qa m o ββββββω对应一个q 有两支格波：一支声学波和一支光学波 , 总的格波数目为2N.2. 具有两维正方点阵的某简单晶格，设原子质量为 M ，晶格常数为 a ，最近邻原子间相互作用的恢复力常数为 c ，假定原子垂直于点阵平面作横振动，试证明：此二维系统的格波色散关系为)cos cos 2(22a q a q c M y x --=ω图二 晶格常数为a 的正方形点阵证明：如图所示，只考虑最近邻原子的作用，第（L ，m ）原子受到（L +1，m ），（L -1，m ），（L ， m +1），（L ，m -1）四个原子的作用力为： （L +1，m ）对它的作用力=)(,,1m L m L u u C -+（L -1，m ）对它的作用力=)(,1,m L m L u u C -- （L ， m +1）对它的作用力=)(,1,m L m L u u C -+ （L ，m -1）对它的作用力=)(1,,--m L m L u u C由于（L +1，m ）和（L -1，m ）对它的作用力以及（L ，m +1）和（L ，m -1）对它的作用力的方向都是相反的，于是相应的运动方程为：C dt u d M m L =2,2 [m L u ,1(+ m L u ,1-+ m L u ,2 -)+(1,+m L u +1,-m L u m L u ,2-)] 用分离变量法，令)()(,y x m L q u q u u =则有C dtx u d Mm L =2,2)(m L u ,1(+m L u ,1-+m L u ,2-) （1）C dt y u d Mm L =2,2)( (1,+m L u +1,-m L u m L u ,2-) （2）则 )(0,)(wt a Lq i m L x e u x u -= （3）)(0,)(wt a Lq i m L x e u y u -= （4）将（3）（4）分别代入其代入运动方程（1）、 （2）后，得到色散关系)cos 1(22a q M c x x-=ω )cos 1(22a q Mc y y -=ω则=2ω2x ω2yω+=Mc 2)cos cos 2(a q a q y x -- )cos cos 2(22a q a q c M y x --=ω二维格子的色散关系)cos cos 2(2)4(2a q a q c e e e e c M y x aq iaiq a iq a iq y y x x --=-+++-=--ω3．求：（a ）一维单原子点阵振动的声子谱密度）（ωρ（频率分布函数），并作图；(b ）一维双原子点阵振动的声子谱密度）（ωρ（频率分布函数），并作图．解：（a ）一维简单晶格的色散关系曲线如图所示，由色散曲线的对称性可以看出，ωd 区间对应两个同样大小的波矢区间dq 。

固体物理第三章晶格振动与晶体的热力学函数第三章晶格振动与晶体的热力学函数一、填空体1. 若在三维空间中，晶体由N 个原胞组成,每个原胞有一个原子,则共有_ 3 N_个独立的振动,_ N__个波矢, 3N_支格波。

2. 体积为V 的ZnS 晶体，如果晶胞的体积为Ω，则晶格振动的模式书为24N/Ω 。

3. 三维绝缘体晶体的低温比热Cv 与温度T 的关系为Cv~T 3。

4. 某三维晶体由N 个原胞组成，每个原胞内有3个原子。

考虑晶体的晶格振动，其色散关系共有 9N 支，其中 3N 支声学波，包括 2N 支横声学波， 1N 支纵声学波；另有 6N 支光学波。

5. 二维绝缘体晶体的低温比热Cv 与温度T 的关系为Cv~T 2。

6. 一维绝缘体晶体的低温比热Cv 与温度T 的关系为Cv~T 。

7. 三维绝缘体晶体的低温平均内能与温度T 的关系为U~T 4。

8.二维绝缘体晶体的低温平均内能与温度T 的关系为U~T 3。

9. 一维绝缘体晶体的低温平均内能温度T 的关系为U~T 2。

10.绝缘体中与温度有关的内能来源于晶格振动能。

11.导体中与温度有关的内能来源于晶格振动能和价电子热运动动能。

12. 某二维晶体由N 个原胞组成，每个原胞内有2个原子。

考虑晶体的晶格振动，其色散关系共有4N 支，其中2N 支声学波，包括N 支横声学波， N 支纵声学波；另有 2N 支光学波。

13. 某一维晶体由N 个原胞组成，每个原胞内有3个原子。

考虑晶体的晶格振动，其色散关系共有 3N 支，其中 N 支声学波，包括 N 支横声学波， 0 支纵声学波；另有 2N 支光学波。

14.晶格振动的元激发为声子，其能量为ω ，准动量为 q。

15德拜模型的基本假设为：格波作为弹性波、介质是各向同性介质。

16.对三维体积为V 的晶体，波矢空间中的波矢密度为：3)2(Vπ ；对二维面积为S 的晶体，波矢空间中的波矢密度为：2)2(S π ；对一维长度为L 的晶体，波矢空间中的波矢密度为：π2L 。