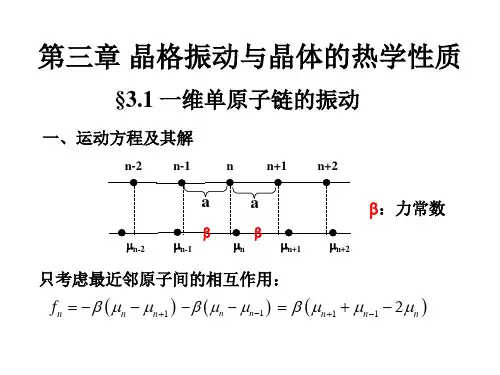
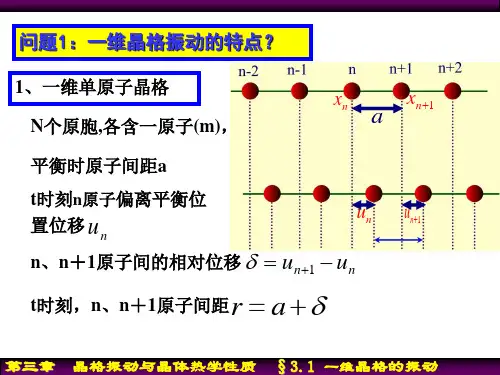
原子的振动 —— 晶格振动在晶体中形成了各种模式的波 —— 简谐近似下,系统哈密顿量是相互独立简谐振动哈密
顿量之和 —— 这些模式是相互独立的,模式所取的能量值是分立的 —— 用一系列独立的简谐振子来描述这些独立而又分立的
振 动模式 —— 这些谐振子的能量量子,称为声子 —— 晶格振动的总体可看作是声子的系综
—— 原子的坐标和简正坐标通过正交变换联系起来
3N
假设存在线性变换 mi i aijQj
j1
系统的哈密顿量
H123iN1Q i2123iN1
Q 2 2
ii
拉格朗日函数
LTV1 23 i N 1Q i21 23 i N 1
Q 2 2
ii
正则动量
pi
—— 谐振子方程
本征态函数 ni(Qi) i exp(22)Hni()
Qi i /
Hni () — 厄密多项式
03_01_简谐近似和简正坐标 —— 晶格振动与晶体的热学性质 10 / 11
N个原子组成的晶体 系统薛定谔方程
[3 i N 11 2 ( 2 Q 2 i2 3 i N 1i2 Q i2 )] (Q 1 , Q 3 N ) E(Q 1 , Q 3 N )
取 V0 0
平衡位置
( V
i
)0
0
—— 不计高阶项
系统的势能函数
V
1 3N ( 2V
2i, j1 ij
)0ij
03_01_简谐近似和简正坐标 —— 晶格振动与晶体的热学性质 05 / 11
系统的势能函数
V1
3N
(
2V
2i, j1 ij
)0ij
[3 i N 11 2 ( 2 Q 2 i2 3 i N 1i2 Q i2 )] (Q 1 , Q 3 N ) E(Q 1 , Q 3 N )