2011年—2018年新课标全国卷1文科数学分类汇编—5.平面向量

2011-2017全国一卷三角函数和平面向量专题汇编（理科学生版）5．（5分）（2011•新课标理）已知角θ的顶点与原点重合，始边与x轴的正半轴重合，终边在直线y=2x上，则cos2θ=（）A．﹣ B．﹣ C．D．11．（5分）（2011•新课标文）设函数，则f（x）=sin（2x+）+cos（2x+），则（）A．y=f（x）在（0，）单调递增，其图象关于直线x=对称B．y=f（x）在（0，）单调递增，其图象关于直线x=对称C．y=f（x）在（0，）单调递减，其图象关于直线x=对称D．y=f（x）在（0，）单调递减，其图象关于直线x=对称10．（5分）（2011•新课标理）已知与均为单位向量，其夹角为θ，有下列四个命题P1：|+|＞1⇔θ∈[0，）；P2：|+|＞1⇔θ∈（，π]；P3：|﹣|＞1⇔θ∈[0，）；P4：|﹣|＞1⇔θ∈（，π]；其中的真命题是（）A．P1，P4B．P1，P3C．P2，P3D．P2，P411．（5分）（2011•新课标理）设函数f（x）=sin（ωx+φ）+cos（ωx+φ）的最小正周期为π，且f（﹣x）=f（x），则（）A．f（x）在单调递减B．f（x）在（，）单调递减C．f（x）在（0，）单调递增D．f（x）在（，）单调递增13．（5分）（2011•新课标）已知a与b为两个垂直的单位向量，k为实数，若向量+与向量k﹣垂直，则k=．15．（5分）（2011•新课标文）△ABC中，∠B=120°，AC=7，AB=5，则△ABC的面积为．16．（5分）（2011•新课标理）在△ABC中，B=60°，AC=，则AB+2BC的最大值为．9．（5分）（2012•新课标理）已知ω＞0，函数f（x）=sin（ωx+）在区间[，π]上单调递减，则实数ω的取值范围是（）A．B．C． D．（0，2]13．（5分）（2012•新课标）已知向量夹角为45°，且，则=．17．（12分）（2012•新课标理）已知a，b，c分别为△ABC三个内角A，B，C的对边，c=asinC﹣ccosA．（1）求A；（2）若a=2，△ABC的面积为，求b，c．9．（5分）（2012•新课标）已知ω＞0，0＜φ＜π，直线x=和x=是函数f （x）=sin（ωx+φ）图象的两条相邻的对称轴，则φ=（）A．B．C．D．10．（5分）（2013•新课标Ⅰ）已知锐角△ABC的内角A，B，C的对边分别为a，b，c，23cos2A+cos2A=0，a=7，c=6，则b=（）A．10 B．9 C．8 D．513．（5分）（2013•新课标Ⅰ）已知两个单位向量，的夹角为60°，=t+（1﹣t）．若•=0，则t=．13．（5分）（2013•新课标Ⅰ）已知两个单位向量，的夹角为60°，=t+（1﹣t）．若•=0，则t=．15．（5分）（2013•新课标Ⅰ理）设当x=θ时，函数f（x）=sinx﹣2cosx取得最大值，则cosθ=．17．（12分）（2013•新课标Ⅰ理）如图，在△ABC中，∠ABC=90°，AB=，BC=1，P为△ABC内一点，∠BPC=90°．（1）若PB=，求PA；（2）若∠APB=150°，求tan∠PBA．2．（5分）（2014•新课标Ⅰ）若tanα＞0，则（）A．sinα＞0 B．cosα＞0 C．sin2α＞0 D．cos2α＞06．（5分）（2014•新课标Ⅰ）设D，E，F分别为△ABC的三边BC，CA，AB的中点，则+=（）A．B．C．D．8．（5分）（2014•新课标Ⅰ理）设α∈（0，），β∈（0，），且tanα=，则（）A．3α﹣β=B．3α+β=C．2α﹣β=D．2α+β=15．（5分）（2014•新课标Ⅰ）已知A，B，C为圆O上的三点，若=（+），则与的夹角为．16．（5分）（2014•新课标Ⅰ）如图，为测量山高MN，选择A和另一座的山顶C 为测量观测点，从A点测得M点的仰角∠MAN=60°，C点的仰角∠CAB=45°以及∠MAC=75°；从C点测得∠MCA=60°，已知山高BC=1000m，则山高MN=m．16．（5分）（2014•新课标Ⅰ理）已知a，b，c分别为△ABC的三个内角A，B，C 的对边，a=2且（2+b）（sinA﹣sinB）=（c﹣b）sinC，则△ABC面积的最大值为．2．（5分）（2015•新课标Ⅰ）已知点A（0，1），B（3，2），向量=（﹣4，﹣3），则向量=（）A．（﹣7，﹣4）B．（7，4） C．（﹣1，4）D．（1，4）2．（5分）（2015•新课标Ⅰ理）sin20°cos10°﹣cos160°sin10°=（）A．B．C．D．8．（5分）（2015•新课标Ⅰ理）函数f（x）=cos（ωx+φ）的部分图象如图所示，则f（x）的单调递减区间为（）A．（kπ﹣，kπ+，），k∈z B．（2kπ﹣，2kπ+），k∈zC．（k﹣，k+），k∈z D．（，2k+），k∈z17．（12分）（2015•新课标Ⅰ理）已知a，b，c分别是△ABC内角A，B，C的对边，sin2B=2sinAsinC．（Ⅰ）若a=b，求cosB；（Ⅱ）设B=90°，且a=，求△ABC的面积．4．（5分）（2016•新课标Ⅰ理）△ABC的内角A、B、C的对边分别为a、b、c．已知a=，c=2，cosA=，则b=（）A．B．C．2 D．36．（5分）（2016•新课标Ⅰ理）将函数y=2sin（2x+）的图象向右平移个周期后，所得图象对应的函数为（）A．y=2sin（2x+）B．y=2sin（2x+）C．y=2sin（2x﹣）D．y=2sin（2x﹣）12．（5分）（2016•新课标Ⅰ理）若函数f（x）=x﹣sin2x+asinx在（﹣∞，+∞）单调递增，则a的取值范围是（）A．[﹣1，1]B．[﹣1，]C．[﹣，]D．[﹣1，﹣]13．（5分）（2016•新课标Ⅰ）设向量=（m，1），=（1，2），且|+|2=||2+||2，则m=．13．（5分）（2016•新课标Ⅰ）设向量=（x，x+1），=（1，2），且⊥，则x=．14．（5分）（2016•新课标Ⅰ）已知θ是第四象限角，且sin（θ+）=，则tan （θ﹣）= ．17．（12分）（2016•新课标Ⅰ）△ABC的内角A，B，C的对边分别为a，b，c，已知2cosC（acosB+bcosA）=c．（Ⅰ）求C；（Ⅱ）若c=，△ABC的面积为，求△ABC的周长．8．（5分）（2017•新课标Ⅰ）函数y=的部分图象大致为（）A．B．C．D．9．（5分）（2017•新课标Ⅰ）已知曲线C1：y=cosx，C2：y=sin（2x+），则下面结论正确的是（）A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2C．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2D．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C211．（5分）（2017•新课标Ⅰ）△ABC的内角A，B，C的对边分别为a，b，c，已知sinB+sinA（sinC﹣cosC）=0，a=2，c=，则C=（）A．B．C．D．13．（5分）（2017•新课标Ⅰ）已知向量=（﹣1，2），=（m，1），若向量+与垂直，则m=．15．（5分）（2017•新课标Ⅰ）已知α∈（0，），tanα=2，则cos（α﹣）=．13．（5分）（2017•新课标Ⅰ）已知向量，的夹角为60°，||=2，||=1，则|+2|=．17．（12分）（2017•新课标Ⅰ理）△ABC的内角A，B，C的对边分别为a，b，c，已知△ABC的面积为．（1）求sinBsinC；（2）若6cosBcosC=1，a=3，求△ABC的周长．。

2011年—2018年新课标全国(quán ɡuó)卷Ⅰ文科数学分类汇编10．解析几何一、选择题(2018·新课标Ⅰ，文4)已知椭圆：的一个焦点为，则C的离心率为（）A．B．C．D．【2017，5】已知是双曲线的右焦点，是C上一点，且与轴垂直，点的坐标是，则的面积为（）仅归朱欢A． B． C． D．【2017，12】设A、B是椭圆C：长轴的两个端点，若C上存在点M满足∠AMB=120°，则m的取值范围是( )A．B． C． D．【2016，5】直线经过椭圆的一个顶点和一个焦点，若椭圆中心到l的距离为其短轴长的，则该椭圆的离心率为（）A．13B．12C．23D．【2015，5】已知椭圆E的中心为坐标原点，离心率为12，E的右焦点与抛物线C:y2=8x，的焦点重合，A,B是C的准线与E的两个交点，则|AB|=( )A．3 B．6 C．9 D．12【2014，10】已知抛物线C：y2=x的焦点为F，A(x0,y0)是C上一点，|AF|=，则x0=( ) A．1 B．2 C．4 D．8【2014，4】4．已知双曲线的离心率为2，则a=( )A．2 B． C． D．1【2013，4】已知双曲线C：(a＞0，b＞0)的离心率为，仅归朱欢则C的渐近线方程为()．A．y＝ B．y＝C．y＝ D．y＝±x【2013，8】O为坐标(zuòbiāo)原点，F为抛物线C：y2＝的焦点，P为C上一点，若|PF|＝，则△POF的面积为()A．2 B． C． D．4【2012，4】设、是椭圆E：（）的左、右焦点，P为直线上一点，是底角为30°的等腰三角形，则E的离心率为（）A．12B．23C．34D．【2012，10】等轴双曲线C的中心在原点，仅归朱欢焦点在x轴上，C与抛物线的准线交于A，B两点，，则C的实轴长为（）A．B．22C．4 D．8【2011，4】椭圆的离心率为仅归朱欢（）A．13B．12C． D．【2011，9】已知直线l过抛物线的焦点，且与C的对称轴垂直，l与C交于A，两点，，P为C的准线上一点，则的面积为（）．A． B． C． D．二、填空题(2018·新课标Ⅰ，文15)直线与圆仅归朱欢交于，两点，则 . 【2016，15】设直线与圆相交于两点，若，则圆C的面积为．【2015，16】已知F是双曲线C:的右焦点，P是C左支上一点，，当ΔAPF周长最小时，该三角形的面积为．三、解答题(2018·新课标Ⅰ，文20)设抛物线，点，，过点A的直线(zhíxiàn)l与C交于，两点.（1）当l与x轴垂直时，求直线的方程；（2）证明：.【2017，20】设A，B为曲线C：上两点，A与B的横坐标之和为4．（1）求直线AB的斜率；（2）设M为曲线C上一点，C在M处的切线与直线AB平行，且，求直线AB的方程．【2016，20】在直角坐标系中，直线交轴于点M，交抛物线于点P，M关于点P的对称点为N，连结并延长交C于点．（1）求；（2）除H以外(yǐwài)，直线与C是否有其他公共点？请说明理由．【2015，20】已知过点A(0, 1)且斜率为k的直线l与圆C：(x-2)2+(y-3)2=1交于M,N两点.(Ⅰ)求k的取值范围； (Ⅱ)=12，其中O为坐标原点，求|MN|.【2014，20】已知点，圆C:，过点P的动直线l与圆C交于两点，线段的中点为M，为坐标原点.(1)求M的轨迹(guǐjì)方程；(2)当时，求l的方程及的面积.【2013，21】已知圆M：(x＋1)2＋y2＝1，圆N：(x－1)2＋y2＝9，动圆P与圆M外切并且与圆N内切，圆心P的轨迹为曲线C.(1)求C的方程；(2)l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P的半径最长时，求|AB|.【2012，20】设抛物线C：（）的焦点为F，准线为l，A为C上一点，已知以F为圆心，FA为半径的圆F交l于B，D两点。

2011-2018高考真题全国卷文科数学试题分类汇编含答案第一章 集合与常用逻辑用语1.（2011全国1文1）已知集合，，，则的子集共有（ ）.A.个B.个C.个D.个 2.(2012全国文1)已知集合，，则（ ）.A. B. C. D. 3.（2013全国I 文1）已知集合，则（ ）.A. B. C. D. 4.（2013全国II 文1）已知集合，，则（ ）.A. B. C. D.5（2014新课标Ⅰ文1）已知集合，，则（ ）A. B. C. D.6.（2014新课标Ⅱ文1）已知集合，，则（ ）A. B. C. D. 7. (2015全国I 文1)已知集合，则集合中元素的个数为（ ）.A. 5B. 4C. 3D. 28. (2015全国II 文1)已知集合，，则（ ）. A. B. C. D. 9. (2016全国I 文1)设集合，，则（B )10.(2016全国II 文1)已知集合，则(D )（A ） （B ） （C ） （D ） 11．(2017全国I 文1)已知集合A ={}|2x x <，B ={}|320x x ->，则 ( A ){}0,1,2,3,4M ={}1,3,5N =P MN =P 2468{}220A x x x =<－－{}11B x x =<<－A B ⊂≠B A ⊂≠A B =AB =∅{}{}21234A B x x n n A ===∈，，，，，A B ={}14，{}23，{}916，{}12，{}|31M x x =-<<{}3,2,1,0,1N =---MN ={}2,1,0,1--{}3,2,1,0---{}2,1,0--{}3,2,1---{|13}M x x =-<<{|21}N x x =-<<MN =(2,1)-(1,1)-(1,3))3,2(-{}2,0,2A =-{}2|20B x x x =--=AB =∅{}2{}0{}2-{32,},{6,8,10,12,14}A x x n n B ==+∈=N A B {|12}A x x =-<<{}03B x x =<<=B A ()13,-()10,-()02,()23,{1,3,5,7}A ={|25}B x x =≤≤A B ={123}A =，，，2{|9}B x x =<A B ={210123}--，，，，，{21012}--，，，，{123}，，{12}，A ．{1,3}B ．{3,5}C ．{5,7}D ．{1,7}A ．AB =3|2x x ⎧⎫<⎨⎬⎩⎭B ．A B =∅C ．AB 3|2x x ⎧⎫=<⎨⎬⎩⎭D ．A B=R12(2017全国II 文1设集合{}{}123234A B ==，，， ，，， 则=AB （A ）A. {}123,4，，B. {}123，，C. {}234，，D. {}134，，13.【2018全国一文1】已知集合{}02A =，，{}21012B =--，，，，，则A B =（A ）A ．{}02，B ．{}12，C ．{}0D ．{}21012--，，，， 14.【2018全国二文2】已知集合，，则（C ）A ．B ．C ．D ．15.【2018全国三1】已知集合，，则（C ）A ．B ．C ．D ．16.（2014新课标Ⅱ文3）函数在处导数存在，若；是的极值点，则（ ）A.是的充分必要条件B.是的充分条件，但不是的必要条件C.是的必要条件，但不是的充分条件17.（2013全国I 文5）已知命题；命题，则下列命题中为真命题的是（ ）.A. B. C. D. 18.（2014新课标Ⅰ文14）甲.乙.丙三位同学被问到是否去过，，三个城市时， 甲说：我去过的城市比乙多，但没去过城市； 乙说：我没去过城市； 丙说：我们三人去过同一城市； 由此可判断乙去过的城市为.第一章 集合答案 BBACB BDABD AAACC CBA{}1,3,5,7A ={}2,3,4,5B =AB ={}3{}5{}3,5{}1,2,3,4,5,7{|10}A x x =-≥{0,1,2}B =A B ={0}{1}{1,2}{0,1,2}()f x 0x x =0:()0p f x '=0:q x x =()f x p q p q q p q q :2<3x x p x ∀∈R ，32:1q x x x ∃∈=-R ，p q ∧p q ⌝∧p q ∧⌝p q ⌝∧⌝A B C B C第2章 复数1.（2011·新课标全国高考文科·Ｔ2）复数512ii=-( ) A. B. C. D. 2.（2012全国文2）复数的共轭复数是（ ）. A. B. C. D. 3.（2013全国II 文2）（ ）. A.B.D. 4.（2014新课标Ⅰ文3）设，则（ ） A.B.D.5.（2011全国文2）复数（ ）. A. B. C. D. 6.（2013全国I 文2）（ ）.A. B. C. D. 7.（2014新课标Ⅱ文2）（ ）A. B. C. D. 8. (2015全国I 文3)已知复数满足，则（ ）. A.B. C. D.9. (2015全国II 文2)若为实数，且，则（ ）. A.B. C. D.10. (2016全国I 文2)设的实部与虚部相等，其中a 为实数，则a =（ )2i -12i -2i -+12i -+3i2iz -+=+2i +2i -1i -+1i --21i=+211i 1iz =++z =12225i12i=-2i -12i -2i -+12i -+()212i1i +=-11i 2--11i 2-+11i 2+11i 2-13i 1i+=-12i +12i -+12i -12i --z (1)i 1i z -=+z =2i --2i -+2i -2i +a 2i3i 1ia +=++a =4-3-34(12i)(i)a ++11.(2016全国II 文2)设复数z 满足，则= ( )（A ）（B ）（C ）（D ）12． (2017全国I 文3)下列各式的运算结果为纯虚数的是 （ ) A ．i(1+i)2B ．i 2(1-i)C ．(1+i)2D ．i(1+i)13.(2017全国II 文2)（1+i ）（2+i ）= ( )A.1-iB. 1+3iC. 3+iD.3+3i14.(2017全国3文3)下列各式的运算结果为纯虚数的是 ( ) A ．i(1+i)2B ．i 2(1-i)C ．(1+i)2D ．i(1+i)15.(2018全国I 文2)设1i2i 1iz -=++，则z = ( ) A ．0B ．12C ．1 D16.【2018全国2卷1】A ．B ．C ．D ．17.【2018全国3卷2】 A ．B ．C ．D ．第2章 复数答案 CDCBC BBCDA CCBAC DDi 3i z +=-z 12i -+12i -32i +32i -()i 23i +=32i -32i +32i --32i -+()()1i 2i +-=3i --3i -+3i -3i +A ．－3 B ．－2 C ．2 D ．3第3章 平面向量1.（2011全国文13）已知与为两个不共线的单位向量，为实数，若向量与向量垂直， 则．2.（2012全国文15）已知向量夹角为，且，，则3.（2013全国I 文13）已知两个单位向量的夹角为，，若，则4.（2013全国II 文14）已知正方形的边长为，为的中点，则__.5.（2014新课标Ⅱ文4）设向量满足（ ）A. B. C. D.6.（2014新课标Ⅰ文6）设分别为的三边的中点，则（ ）A.B.C. D. 7.(2015全国II 文7)已知三点，，，则外接圆的圆心到原点的距离为（ ）.A. B.C. D. 8.(2015全国I 文2) 已知点，向量，则向量（ ）.A. B. C. D. 9.(2015全国II 文4)向量,，则（ ）. A.B. C. D.10．（2016全国文15）设向量a =(x ，x +1)，b =(1，2)，且a ⊥b ，则x =11.(2016全国II 文13)已知向量a =(m ,4)，b =(3,-2)，且a ∥b ，则m =________.12．（2017全国文13）已知向量a =（–1，2），b =（m ，1）.若向量a +b 与a 垂直，则m =____________. 13.(2017全国II 文)设非零向量a ，b 满足+=-b b a a 则（ ）A a ⊥b B. =b a C. a ∥b D. >b a14．（2018全国1文7）在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB = （ ） A ．3144AB AC - B ．1344AB AC - C ．3144AB AC +D ．1344AB AC + a b k +a b k -a b k =,a b 451=a 2-=a b =b ，a b 60()1t t =+-c a b 0⋅=b c t =ABCD 2E CD AE BD ⋅=，a b +=a b -a b ⋅=a b 1235F E D ,,ABC △AB CA BC ,,=+2121()1,0A (B (C ABC △3532135234(0,1),(3,2)A B ()4,3AC =--BC =()7,4--()7,4()1,4-()1,4()1,1=-a ()1,2=-b ()2+⋅=a b a 1-012开始结束开始结束答案：1、 1 ， 2、，3、3 ，4、2， 5A ，6A ，7B ，8A ， 9C ，1011 -6 12 7 13 A第4章 算法初步1.（2013全国II 文7）执行右面的程序框图，如果输入的，那么输出的（ ）.A. B. C. D. 2.（2013全国I 文7）7. 执行右面的程序框图，如果输入的，则输出的属于（ ）.A.B.C.D. 3.（2014新课标Ⅰ文9）执行如图所示的程序框图，若输入的分别为1,2,3，则输出的（ ）A. B. C. D.第3题 第2题 第1题4.（2011全国文5）执行如图所示的程序框图，如果输入的是6，则输出的是（ ）. A. B. C.D.=b 23-4N =S =1111234+++1111232432+++⨯⨯⨯111112345++++111112324325432++++⨯⨯⨯⨯⨯⨯[]13t ∈-，s []34-，[]52-，[]43-，[]25-，,,a b k M =20372165158N p 120720144050405.（2014新课标Ⅱ文8）执行如下图所示程序框图，如果输入的均为，则输出的（ ） A. B. C. D.6.（2012全国文6）如果执行下边的程序框图，输入正整数和市属，输出，则 ( )A.为的和B.为的算术平均数 C.和分别是中最大的数和最小的数 D.和分别是第4题 第5题 6题7.(2015全国I 文9)执行如下图所示的程序框图，如果输入的，则输出的（ ）.A. 5B. 6C.D.8. (2015全国II 文8)如下图所示，程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图，若输入的.分别为14.18，则输出的（ ）. A. B. C. D.9.(2016全国I 文10).执行下面的程序框图，如果输入的 n =1,则输出的值满足( )（A ） （B ） （C ） （ D ）,x t 2S =4567()2N N …12,,...,N a a a ,A B A B +12,,...,N a a a 2A B+12,,...,N a a a A B 12,,...,N a a a A B 12,,...,N a a a 0.01t =n =78a b a =024140,1,x y ==,x y 2y x =3y x =4y x =5y x =第7题 第8题 第9题 10．(2017全国I 文10)如图是为了求出满足321000n n ->的最小偶数n ，那么在和两个空白框中，可以分别填入 ( )A ．A >1000和n =n +1B ．A >1000和n =n +2C ．A ≤1000和n =n +1D ．A ≤1000和n =n +2答案：BADBD CCBCDnm1S=1,n=0,m=12?输入t否第5章 三角函数与解三角形1.（2014全国I 文2）若，则（）A. B. C. D. 2.（2011全国文11）设函数，则（）. A.在单调递增，其图象关于直线对称 B.在单调递增，其图象关于直线对称 C.在单调递减，其图象关于直线对称 D.在单调递减，其图象关于直线对称 3. .在函数①，②，③，④中，最小正周期为的所有函数为（）A.①②③B. ①③④C. ②④D. ①③4.（2014新课标Ⅱ文14）函数的最大值为5.（2012全国文9）已知，直线和是函数图像的两条相邻的对称轴，则（）. A.B. C. D.6.(2015全国I 文8) 函数的部分图像如图所示，则的单调递减区间为（）. A. B.C. D.7.（2013全国II 文16）函数的图象向右平移个tan 0α>sin 0α>cos 0α>sin 20α>cos20α>ππ()sin 2cos 244f x x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭()f x π0,2⎛⎫ ⎪⎝⎭π4x =()f x π0,2⎛⎫ ⎪⎝⎭π2x =()f x π0,2⎛⎫ ⎪⎝⎭π4x =()f x π0,2⎛⎫ ⎪⎝⎭π2x =cos 2y x =cos y x =cos 26y x π⎛⎫=+ ⎪⎝⎭tan 24y x π⎛⎫=- ⎪⎝⎭π()sin()2sin cos f x x x ϕϕ=+-0ω>0ϕ<<π4x π=4x 5π=()()sin f x x ωϕ=+ϕ=4π3π2π43π()cos()f x x ωϕ=+()f x ()13π,π44k k k ⎛⎫-+∈ ⎪⎝⎭Z ()132π,2π44k k k ⎛⎫-+∈ ⎪⎝⎭Z ()13,44k k k ⎛⎫-+∈ ⎪⎝⎭Z ()132,244k k k ⎛⎫-+∈ ⎪⎝⎭Z cos(2)(ππ)y x ϕϕ=+-剟π2单位后，与函数的图象重合，则_________. 8.（2011全国1文7）已知角的顶点与原点重合，始边与轴的正半轴重合，终边在直线上，则（）.A. B. C. D. 9.（2013全国II 文6）已知，则（）.A.B.C. D.10.(2013全国I 文9)函数在的图象大致为（）.11.(2013全国I 文16)设当时，函数取得最大值，则.12.(2015全国II 文11)如图所示，长方形的边，，是的中点，点沿着，与运动，记.将动点到，两点距离之和表示为的函数，则的图像大致为（）.πsin 23y x ⎛⎫=+⎪⎝⎭ϕ=θx 2y x =cos2θ=45-35-35452sin 23α=2πcos 4α⎛⎫+= ⎪⎝⎭16131223()()1cos sin f x x x =-[]ππ-，D.C.B.A.x θ=()sin 2cos f x x x =-cos θ=ABCD 2AB =1=BC O AB P BC CD DA BOP x ∠=P A B x ()f x ()y f x =A. B. C. D.13.（2013全国II 文4）的内角的对边分别为，已知，，，则的面积为（）.A. B.C.14.(2015全国II 文17)中，是上的点，平分，. ，求.15.（2011全国文15）中，，，，则的面积为．16.（2013全国I 文10）已知锐角的内角的对边分别为，，，，则（）.A. B. C. D.17.（2014新课标Ⅱ文17）（本小题满分12分）四边形的内角与互补，，，.（1）求和；（2）求四边形的面积.424424424424ABC △,,A B C ,,a b c 2b =π6B =π4C =ABC△2121ABC △D BC AD BAC ∠2BD DC =60BAC =B ∠ABC △120B =7AC =5AB =ABC △ABC △A B C ，，a b c ，，223cos cos20A A +=7a =6c =b =10985ABCD A C 1AB =3BC =2CD DA ==C BD ABCD18.（2012全国文17）已知分别为△三个内角的对边， （1）求；（2）若，△.19.（2014新课标Ⅰ文16）如图所示，为测量山高，选择和另一座山的山顶为测量观测点.从点测得点的仰角，点的仰角以及；从点测得.已知山高，则山高20. (2015全国I 文17)已知分别为内角的对边，.（1）若，求；（2）设，且的面积.２１. (2015全国I 文４)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知，，，则b=（）,,a b c ABC ,,A B C sin cos c C c A =-A 2a =ABC ,b c MN A C A M 60MAN ∠=︒C 45CAB ∠=︒75MAC ∠=︒C 60MCA ∠=︒100m BC =MN =,,a b c ABC △,,A B C 2sin 2sin sin B A C =a b =cos B 90B ∠=a =ABC △a =2c =2cos 3A =A BC ．2D ．3２２. (2016全国I 文６)若将函数y =2sin (2x +π6)的图像向右平移14个周期后，所得图像对应的函数为２３. (2016全国I 文1４)已知θ是第四象限角，且sin (θ+)=，则tan (θ–)= 24 (2017全国I 文8)．函数sin21cos xy x=-的部分图像大致为A ．B ．C ．D ．25. (2017全国I 文15)．已知π(0)2α∈，，tan α=2，则πcos ()4α-=__________．26.(2018全国I 文8)．已知函数()222cos sin 2f x x x =-+，则 （ ）A ．()f x 的最小正周期为π，最大值为3B ．()f x 的最小正周期为π，最大值为4C ．()f x 的最小正周期为2π，最大值为3D ．()f x 的最小正周期为2π，最大值为427.(2018全国I 文11)．已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点()1A a ，，()2B b ，，且2cos 23α=，则a b -= （ ）A ．15BCD ．128.(2018全国I 文16)．△ABC 的内角A B C ，，的对边分别为a b c ，，，已知sin sin 4sin sin b C c B a B C +=，2228b c a +-=，则△ABC 的面积为________．π435π4A ． y =2sin(2x +π4)B ． y =2sin(2x +π3)C ． y =2sin(2x –π4)D ． y =2sin(2x –π3)高考真题试题详解1.解析由得是第一.三象限角，若是第三象限角，则A ，B 错； 由知，C 正确；取时，，D 错.故选C. 评注本题考查三角函数值的符号，判定时可运用基本知识.恒等变形及特殊值等多种方法，具有一定的灵活性.2.解析因为，当时，，故在单调递减. 又当是的一条对称轴.故选D.3.解析①，最小正周期为；②由图像知的最小正周期为；③的最小正周期；④的最小正周期.因此选A.评注本题考查三角函数的周期性，含有绝对值的函数可先变形再判断，或运用图像判断其最小正周期. 4.解析，所以.5.分析利用三解函数的对称轴求得周期.解析由题意得周期，所以，即，所以，所以 ，.因为，所以. 所以，所以.故选A. 6.解析由图可知，得，.画出图中函数的一条对称轴，如图tan 0α>ααsin 22sin cos ααα=sin 20α>απ32211cos 22cos 121022αα⎛⎫=-=⨯-=-< ⎪⎝⎭ππππ()sin 2cos 2sin 2cos 24444f x x x x x ⎛⎫⎛⎫⎛⎫=+++=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭π02x <<02πx <<()f x x =π0,2⎛⎫⎪⎝⎭π2x =π22⎛⎫⨯= ⎪⎝⎭π2x =()y f x =cos 2cos 2y x x ==πcos y x =ππcos 26y x ⎛⎫=+⎪⎝⎭2ππ2T ==πtan 24y x ⎛⎫=- ⎪⎝⎭π2T =()()sin 2sin cos sin cos cos sin 2sin cos f x x x x x x ϕϕϕϕϕ=+-=+-=()sin cos cos sin sin 1x x x ϕϕϕ-=-…()max 1f x =512ππ2π44T ⎛⎫=-=⎪⎝⎭2π2πω=1ω=()sin()f x x ϕ=+ππsin 144f ϕ⎛⎫⎛⎫=+=± ⎪ ⎪⎝⎭⎝⎭5π5πsin 144f ϕ⎛⎫⎛⎫=+=± ⎪ ⎪⎝⎭⎝⎭0πϕ<<ππ5π444ϕ<+<ππ42ϕ+=π4ϕ=511244T =-=2T =2ππTω==()f x 0x x =所示.由图可知，则，可得，则，得.由，得的单调递减区间为. 故选D.7.分析先进行平移，得出的三角函数与所给的三角函数进行比较，求出的值. 解析：的图象向右平移个单位得到的图象，整理得.因为其图象与的图象重合，所以，所以，即.又因为，所以. 8.解析设为角终边上任意一点，则. 当时，；当时，.因此.故选B.9.分析结合二倍角公式进行求解.解析：因为，所以故选A. 10.分析先利用函数的奇偶性排除B ，再利用特殊的函数值的符号排除A ，而最后答案的选择则利用了特定区间上的极值点.解析：在上，因为，所以是奇函数，所以的图象关于原点对称，排除B.取，则，排除A.因为，所以令，则或. 034x =3πcos 14ϕ⎛⎫+=-⎪⎝⎭3π2ππ4k ϕ+=+()π2π4k k ϕ=+∈Z ()πcos π4f x x ⎛⎫=+ ⎪⎝⎭π2ππ2ππ4k x k ++剟()f x 132244k xk -+剟ϕ()cos 2y x ϕ=+2πcos 22y x ϕ⎡π⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦()cos 2y x ϕ=-π+sin 23y x π⎛⎫=+ ⎪⎝⎭2k ϕππ-π=-+π322k ϕππ=+π-+π322k ϕ5π=+π6ϕ-ππ≤<5ϕπ=6(,2)(0)P t t t ≠θcos θ=0t>cos θ=0t<cos θ=223cos 22cos 1155θθ=-=-=-2sin 23α=221cos 211sin 213cos .42226αααπ⎛⎫++- ⎪π-2⎛⎫⎝⎭+==== ⎪⎝⎭[],-ππ()()()()()1cos sin 1cos sin f x x x x x -=---=--=⎡⎤⎣⎦()()1cos sin x x f x --=-()f x ()f x 2x π=1cos 10f ππ⎛⎫⎛⎫=-= ⎪ ⎪22⎝⎭⎝⎭>()()1cos sin f x x x =-()()sin sin 1cos cos f x x x x x '=⋅+-2221cos cos cos 2cos cos 1.x x x x x =-+-=-++()0f x '=cos 1x =1cos 2x =结合，求得在上的极大值点为，靠近，故选C. 11.分析先利用三角恒等变换求得函数的最大值，再利用方程思想求解. 解析：， 则所以，所以， 所以又因为时，取得取大值，所以.又，所以即.12.解析由已知可得，当点在边上运动时，即时，；当点在边上运动时，即，时，当时，； 当点在边上运动时，即时，.从点的运动过程可以看出，轨迹关于直线对称，，且轨迹非直线型.故选B. 评注本题以几何图形为背景考查了函数图像的识别与作法，特别是体现了分类讨论和数形结合的思想. 13.分析先由正弦定理解出的值，再运用面积公左求解. 解析：因为，，所以 由正弦定理，得，即所以.故选B. 14.分析 (1)根据题意，由正弦定理可得.[],x ∈-ππ()f x (]0,π23ππsin 2cos y x x x x ⎫=-=⎪⎭cos sin αα=)()sin cos cossin .y x x ααα=-=-x ∈R x α-∈R max y =x θ=()f x ()sin 2cos fθθθ=-=22sin cos 1θθ+=sin cos θθ⎧=⎪⎪⎨⎪=⎪⎩cos θ=P BC π04x剟PA PB +=tan x P CD π3π44x 剎?π2x ≠PA PB +=π2x =PA PB +=P AD 3ππ4x 剎?tan PA PB x +=P π2x =ππ42f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭c 6B π=4C π=7.A B C πππ=π--=π--=6412sin sin b c B C =2sin sin c =ππ64212=c =117sin 212212ABC S bc A π==⨯⨯=△sin 1sin 2B DC C BD ∠==∠(2)由诱导公式可得，由(1)可知，所以，. 解析 (1)由正弦定理得，，.因为平分，，所以. (2)因为，，所以.由(1)知，所以，即. 评注三角是高中数学的重点内容，在高考中主要利用三角函数，三角恒等变换及解三角形的正弦定理及余弦定理，在求解时，注意角的转化及定理的使用.15.解析由余弦定理知，即，解得．故．故答案为． 16.分析先求出角的余弦值，再利用余弦定理求解.解析：由得，解得.因为是锐角，所以.又，所以，所以或.又因为，所以.故选D.17.解析（1）由题设及余弦定理得，①. ②由①，②得，故，()1sin sin sin 22C BAC B B B ∠=∠+∠=∠+∠2sin B ∠=sin C ∠tan 3B ∠=30B ∠=sin sin AD BD B BAD =∠∠sin sin AD DCC CAD=∠∠AD BAC ∠2BD DC =sin 1sin 2B DC C BD ∠==∠()180C BAC B ∠=-∠+∠60BAC ∠=()1sin sin sin 2C BAC B B B ∠=∠+∠=∠+∠2sin sin B C ∠=∠tan 3B ∠=30B ∠=2222cos120AC AB BC AB BC =+-⋅249255BC BC =++3BC =11sin120532224ABC S AB BC =⋅=⨯⨯⨯=△4A 223cos cos 20A A +=2223cos 2cos 10A A +-=1cos 5A =±A 1cos 5A =2222cos a b c bc A =+-214936265b b =+-⨯⨯⨯5b =135b =-0b >5b >2222cos 1312cos BD BC CD BC CD C C =+-⋅=-2222cos 54cos BD AB DA AB DA A C =+-⋅=+1cos 2C =60C =BD =（2）四边形的面积评注本题考查余弦定理的应用和四边形面积的计算，考查运算求解能力和转化的思想，把四边形分割成两个三角形是求面积的常用方法.18.解析（1）由.由于,所以. 又，故. （2）的面积，故.而，故 . 解得.19.解析在中，，，所以. 在中，，，从而，由正弦定理得，，因此.在中，，，由得，故填.20. 解析（1）由正弦定理得，.又，所以，即.则. （2）解法一：因为，所以，即，亦即.又因为在中，，所以，则，得.所以为等腰直角三角形，得，所以. 解法二：由（1）可知，①因为，所以，②将代入得，则，所以.ABCD 1111sin sin 1232sin 60232222S AB DA A BC CD C ⎛⎫=⋅+⋅=⨯⨯+⨯⨯= ⎪⎝⎭sin cos c C c A =-sinA C -cos sin sin 0A C C -=sin 0C ≠π1sin 62A ⎛⎫-= ⎪⎝⎭0πA <<π3A =ABC △1sin 2S bc A ==4bc =2222cos a b c bc A =+-228b c +=2b c ==Rt ABC △45CAB ∠=100BC =m AC =m AMC △75MAC ∠=60MCA ∠=45AMC ∠=sin 45sin 60AC AM=AM=m Rt MNA △AM =m 60MAN∠=sin 60MNAM=150MN ==m 15022b ac =a b =22a ac=2a c =22222212cos 2422a a a a cb B a ac a ⎛⎫+- ⎪+-⎝⎭===⋅90B ∠=()2sin 12sin sin 2sin sin 90B A C A A ===-2sin cos 1A A =sin 21A =ABC △90B ∠=090A <∠<290A ∠=45A ∠=ABC △a c ==112ABC S ==△22b ac =90B ∠=222a c b +=②①()20a c -=a c ==112ABC S ==△２１. (2015全国I 文４)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知，，，则b=答案：D解析：本题考察余弦定理，根据题目条件画出图形可以列出等式,带入已知条件化简可得，解得.２２. (2016全国I 文６)若将函数y =2sin (2x +π6)的图像向右平移14个周期后，所得图像对应的函数为答案：D解析：该函数的周期为,所以函数向右平移，得，化简可得y =2sin(2x –π3).２３. (2016全国I 文1４)已知θ是第四象限角，且sin (θ+)=，则tan (θ–)=.答案： 解析：本题考察同角的三角函数关系，三角函数的符号判断以及诱导公式的运用：，因为θ是第四象限角，且，所以也在第四象限，即，所以24 (2017全国I 文8)．函数sin21cos xy x=-的部分图像大致为a =2c =2cos 3A =2222cos a b c bc A =+-23830b b --=3b =2T ππω==4π2sin(2())46y x ππ=-+π435π443-cos()4πθ-=3cos()sin()4245πππθθ+-=+=cos()4πθ-=354πθ-4sin()45πθ-=-sin()44tan()43cos()4πθπθπθ--=--ABC ．2D ．3A ． y =2sin(2x +π4) B ． y =2sin(2x +π3)C ． y =2sin(2x –π4)D ． y =2sin(2x –π3)A ．B ．C ．D ．【答案】C【解析】由题意知，函数sin 21cos xy x=-为奇函数，故排除B ；当πx =时，0y =，故排除D ；当1x =时，sin 201cos 2y =>-，故排除A ．故选C ．25. (2017全国I 文15)．已知π(0)2α∈，，tan α=2，则πcos ()4α-=__________．26.(2018全国I 文8)．已知函数()222cos sin 2f x x x =-+，则 B A ．()f x 的最小正周期为π，最大值为3 B ．()f x 的最小正周期为π，最大值为4 C ．()f x 的最小正周期为2π，最大值为3 D ．()f x 的最小正周期为2π，最大值为427.(2018全国I 文11)．已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点()1A a ，，()2B b ，，且2cos 23α=，则a b -= BA ．15B C D ．128.(2018全国I 文16)．△ABC 的内角A B C ，，的对边分别为a b c ，，，已知sin sin 4sin sin b C c B a B C +=，2228b c a +-=，则△ABC 的面积为．第6章 极坐标与参数方程1．（2013全国2文23）动点都在曲线（为参数）上，对应参数分别为与（），为的中点.（1）求的轨迹的参数方程；（2）将到坐标原点的距离表示为的函数，并判断的轨迹是否过坐标原点.2.（2014新课标Ⅱ文23）在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，半圆的极坐标方程为，.（1）求的参数方程；（2）设点在上，在处的切线与直线垂直，根据（1）中你得到的参数方程，确定的坐标.P Q ，2cos 2sin x tC :y t=⎧⎨=⎩t t α=2t α=0<<2παM PQ M M d a M xOy x C 2cos ρθ=0,2θπ⎡⎤∈⎢⎥⎣⎦C D C CD :2l y =+D3（2012全国文23）已知曲线的参数方程是为参数，以坐标原点为极点，轴的正半轴为极轴建立坐标系，曲线的极坐标方程是，正方形的顶点都在上，且依逆时针次序排列，点的极坐标为.（1）求点的直角坐标； （2）设为上任意一点，求的取值范围.4.(2015全国II 文23) 在直线坐标系中，曲线：（为参数，）其中.(1) 求与交点的直角坐标；1C 12cos ,:3sin ,x C y ϕϕ=⎧⎨=⎩(ϕ)x 2C 2ρ=ABCD 2C ,,,A B C D A π2,3⎛⎫⎪⎝⎭,,,A B C D P 1C 2222PA PB PC PD +++xOy 1C cos sin x t y t αα=⎧⎨=⎩t 0t ≠0πα剟2C 3C5.(2015全国I 文23)在直角坐标系中，直线：，圆：，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系. （1）求的极坐标方程. （2）若直线的极坐标方程为，设与的交点为，求的面积.6.（2011全国文23））在直角坐标系中，曲线的参数方程为（为参数），是上的动点，点满足，点的轨迹为曲线．（1）求的方程；（2）在以为极点，轴的正半轴为极轴的极坐标系中，射线与的异于极点的交点为，与的异于极点的交点为，求．xOy 1C 2x =-2C ()()22121x y -+-=12,C C 3C ()π4θρ=∈R 2C 3C ,M N 2C MN △xOy 1C 2cos ,22sin .x y αα=⎧⎨=+⎩αM 1C P 2OP OM =P 2C 2C O x π3θ=1C A 2C B AB7（2013全国I 文23）已知曲线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.（1）把的参数方程化为极坐标方程；（2）求与交点的极坐标8（2016全国卷1 23.）（本小题满分10分）选修4—4：坐标系与参数方程 在直线坐标系xoy 中，曲线C 1的参数方程为（t 为参数，a ＞0）。

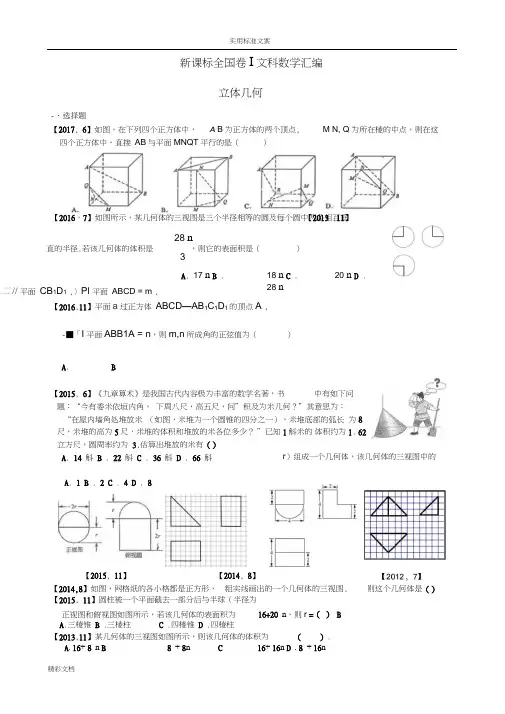
新课标全国卷I文科数学汇编立体几何-、选择题【2017, 6】如图，在下列四个正方体中，A B为正方体的两个顶点,四个正方体中，直接AB与平面MNQT平行的是（）【2016，7】如图所示，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂28 n直的半径.若该几何体的体积是，则它的表面积是（）3A. 17 n B . 18 n C . 20 n D .28 n【2016,11】平面a过正方体ABCD—AB1C1D1的顶点A ,-■「I平面ABB1A = n，则m,n所成角的正弦值为（）A. B【2015, 6】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问”积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，米堆的体积和堆放的米各位多少？”已知1斛米的体积约为1. 62立方尺，圆周率约为3,估算出堆放的米有（）A. 14 斛B . 22 斛 C . 36 斛D . 66 斛【2015, 11】圆柱被一个平面截去一部分后与半球（半径为正视图和俯视图如图所示，若该几何体的表面积为16+20 n，则r =（） BA.三棱锥 B .三棱柱 C .四棱锥D .四棱柱【2013,11】某几何体的三视图如图所示，则该几何体的体积为（）.M N, Q为所在棱的中点，则在这二// 平面CB1D1,〉Pl 平面ABCD = m ,r）组成一个几何体，该几何体的三视图中的A. 1 B . 2 C . 4 D . 8【2015, 11】【2014, 8】【2014,8】如图，网格纸的各小格都是正方形，粗实线画出的一个几何体的三视图,A. 16+ 8 n B8 + 8n C16+ 16n D . 8 + 16n【2013 ,11】则这个几何体是（）A. 6B. 9C. 12D. 15【2012, 7】如图，网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图，则此几何体的体积为【2012, 8】平面〉截球O 的球面所得圆的半径为 1,球心O 到平面〉的距离为迈，则此球的体积为()【2011, 8】在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为()二、 填空题【2017 , 16】已知三棱锥S - ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径.若平面SCA 丄平面SCB, SA= AC , SB = BC ,三棱锥S — ABC 的体积为9,则球O 的表面积为 ____________ .【2013,15】已知H 是球O 的直径AB 上一点，AH ： HB= 1 : 2, AB 丄平面a , H 为垂足，a 截球O 所得截面 的面积为n,则球 O 的表面积为 ___________ . 【2011 , 16】已知两个圆锥由公共底面，且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底面面3积是这个球面面积的 ，则这两个圆锥中，体积较小者的高与体积较大者的高的比值为.16三、 解答题【2017, 18】如图，在四棱锥 P - ABCD 中，AB // CD ，且/BAP /CDP =90 .(1)证明：平面 PAB I 平面 PAD ； ( 2 )若 PA = PD = AB = DC , ._ APD = 90，且四棱锥8P - ABCD 的体积为—，求该四棱锥的侧面积.3A .、、6 二B . 4,3■：C. 4, 6 ■:(A)(D>(C)(D)18】如图四边形 ABCD 为菱形，G 为AC 与 BD 交点,【2015, (I )证明：平面 AECL 平面BED(n )若/ ABC 120°, AEL EC 三棱锥 E- ACD 的体积为—，求该三棱锥的侧面积.3【2016,18】如图所示，已知正三棱锥 P - ABC 的侧面是直角三角形， PA = 6，顶点P 在平面ABC 内的正投影为点D ，D 在平面PAB 内的正投影为点 E •连结PE 并延长交AB 于点G .(1) 求证：G 是AB 的中点；(2) 在题图中作出点 E 在平面PAC 内的正投影F (说明作法及理由)，并求四面体 PDEF 的体积.【2014,19】如图，三棱柱ABC-AB I G中，侧面BB i C i C为菱形，BQ的中点为O，且AO _平面BBQC .（1）证明：BQ _ AB；（2）若AC _ AB,, . CBR =60 ,BC =1,求三棱柱ABC-A^G 的高.【2013，19】如图，三棱柱AB G ABG 中，CA= CB AB= AA，/ BAA= 60 °.(1)证明：ABL A c；(2)若AB= CB= 2，AQ= 6，求三棱柱ABC-A BC 的体积.实用标准文案2【2012,19】如图，三棱柱 ABC- ABC 中，侧棱垂直底面,占八、、♦(1)证明：平面 BDC 丄平面BDC2)平面BDC 分此棱柱为两部分，求这两部分体积的比.【2011,18】如图所示，四棱锥 P -ABCD 中，底面ABCD 为平行四边形，.DAB =60： , AB = 2AD ,PD _ 底面 ABCD . (1) 证明：PA _ BD ;(2) 若PD =AD -1，求棱锥 D -PBC 的高.1NACB=90&, AC=BC=AA , D 是棱 AA 的中21-、选择题【2017, 6】如图，在下列四个正方体中，A ,B 为正方体的两个顶点, 四个正方体中，直接 AB 与平面MNQT 平行的是（）【解法】选 A.由B, AB// MQ 则直线AB//平面MNQ 由C, AB// MQ 则直线AB//平面MNQ 由D, AB// NQ 则直线AB//平面MNQ 故A 不满足，选 A .【2016 , 7】如图所示，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径•若该几28 n，则它的表面积是（ 3M N, Q为所在棱的中点，则在这何体的体积是).A . 17 n18 n C20 n解析：选A. 由三视图可知，该几何体是一个球截去球的-，设球的半径为R ，则--88 3 n R328兀，解得2 .该几何体的表面积等于球的表面积的7，加上3个截面的面积，每个截面是圆面的所以该几何体的表面积为S=74n 22 3 1 n 22 8 4=14 n ' 3n = 17 n .故选 A .【2016, 11】平面：•过正方体ABCD-A 1BC 1D 1的顶点ABCD =平面ABQA ］二n ，则m,n 所成角的正弦值为（2即平面AEF , 即研究AE 与AF 所成角的正弦值，易知—，所以其正弦值为-.故选A .3 2解析：选A 解法一: 将图形延伸出去，构造一个正方体，如图所示.通过寻找线线平行构造出平面:,解法二（原理同解法一）：过平面外一点 A 作平面：•，并使:-II 平面CBjD j ，不妨将点A 变换成B ，作］［，即为平面A,BD ，如图所示，即研究 AB 与BD 所成角【2015, 6】《九章算术》是我国古代内容极为丰富的数学名著,下周八尺，高五尺，问”积及为米几何？ ”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为 8尺，米堆的高为5尺，米堆的体积和堆放 的米各位多少？ ”已知 1斛米的体积约为1. 62立方尺，圆周率约为3，估算 出堆放的米有（）BA . 14 斛B . 22 斛C . 36 斛D . 66 斛116 解：设圆锥底面半径为 r ,依题 2 3r =8= r，所以米堆的体积43,1116 2 320 320 …为3 （ ）2 5 ，故堆放的米约为十1. 62~22,故选B .43 3 99使之满足同等条件，在这样的情况下容易得到 的正弦值，易知NABD =3，所以其正弦值为3-•故选A .2书 中有如下问题：“今有委米依垣内角, E F【2015,11】圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，若该几何体的表面积为16+20 n，则r =（） BA. 1 B . 2 C . 4 D . 8解：该几何体是半球与半个圆柱的组合体，圆柱的半径与球的半径都为r，圆柱的高为2r,其表面积2 2 2 2为 2 n r +n r x 2叶n r +2r x 2r =5 n r +4r =16+20n,解得r=2，故选B.【2014, 8】如图，网格纸的各小格都是正方形，粗实线画出的一个几何体的三视图，则这个几何体是（）BA.三棱锥 B .三棱柱 C .四棱锥D .四棱柱解：几何体是一个横放着的三棱柱. 故选B2B . 8 + 8 nC . 16+ 16 nD . 8 + 16 n该几何体为一个半圆柱与一个长方体组成的一个组合体.2X 2 X 4 = 8 n, V 长方体=4X 2X 2= 16.所以所求体积为 16+ 8 n.故选 A .1,粗线画出的是某几何体的三视图，则此几何体的体积为【解析】由三视图可知，该几何体为 三棱锥A-BCD, 底面△ BCD 为底边为6,高为3的等腰三角形， 侧面ABDL 底面BCD AOL 底面BCD因此此几何体的体积为11V（― 6 3） 3 = 9，故选择 3 2【2012, 8］ 8.平面：•截球O 的球面所得圆的半径为 距离为.2，则此球的体积为（ ）A . 6：B . 4、、3二C. 4 6：D. 6.3二【解析］如图所示，由已知 Q A =1 , 001 =庞,在Rt OO-i A 中，球的半径 R = OA = 3,所以此球的体积 V ■ R 3 — 4 • 3：；：；，故选择B .3【点评］本题主要考察球面的性质及球的体积的计算. 【2011, 8］在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为（）【2013,11】某几何体的三视图如图所示，则该几何体的体积为 )•A . 6B . 9 C. 12 D. 15A . 16+ 8 n 解析：选A.V1V 半圆柱=—n2【2012, 7】如图，网格纸上小正方形的边长为1，球心O 到平面〉的D【解析】由几何体的正视图和侧视图可知，该几何体的底面为半圆和等腰三角形，其侧视图可以是一个由等腰三角形及底边上的高构成的平面图形. 故选D.二、填空题【2017 , 16】已知三棱锥S _ ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径.若平面SCA 丄平面SCB, SA 二AC , SB = BC ，三棱锥S — ABC 的体积为9,则球O 的表面积为 _____________ .【解析】取SC 的中点O ,连接OA,OB ，因为SA 二AC, SB 二BC ,所以OA _ SC,OB _ SC , 因为平面 SAC 丄平面 SBC 所以 OA 丄平面 SBC 设 OA1 1 11 31 3V A SBCS SBC OA2r r r r ，所以—r 9= r = 3,一 3凸3 2 3 3所以球的表面积为 4二r 2 =36二.【2013,15】已知H 是球O 的直径AB 上一点，AH ： HB= 1 : 2, AB 丄平面a , H 为垂足，a 截球O 所得截面 的面积为n,则球 O 的表面积为 ____________ .9答案：一 n2解析：如图，2RR设球0的半径为 R,则AH h,OH k.又EH =n,33•••氏=9. ••• S球=4 n F 2= 9n.8 2【2011,16】已知两个圆锥由公共底面，且两圆锥的顶点和底面的圆周都在同一个球面上.右圆锥底面面3积是这个球面面积的，则这两个圆锥中，体积较小者的高与体积较大者的高的比值为_____16【解析】设圆锥底面半径为 r ，球的半径为R ，则由n 2 - 4 n F 2，知r^-R 2 .16 4根据球的截面的性质可知两圆锥的高必过球心 0,点，因此PB _QB .设 PO =x , QO = y ，则 x y = 2R .— n-r rt-r F 、丄:.EH = 1. v 在 Rt △ OEH 中，F = 仝 +12 ,2丿又△PO B s^ BO Q，知r2 = O B2二xy .即xy = r2= —R2.4由及x.y可得X=|R,_R -则这两个圆锥中，体积较小者的高与体积较大者的高的比为1故答案为丄.3三、解答题【2017, 18】如图，在四棱锥P-ABCD中，AB // CD，且乙BAP £CDP = 90 .(1)证明：平面PAB _ 平面PAD ； ( 2)若PA = PD = AB 二DC,/ APD =90，且四棱锥8P -ABCD 的体积为？，求该四棱锥的侧面积.3【解法】(1) 丁BAP =CDP =90, . AB _ AP, CD _ DP又.AB // CD . AB _ DP又AP 平面PAD , DP 平面PAD，且AP门DP = P . AB _平面PAD AB u平面PAB ,所以平面PAB丄平面PAD(2)由题意：设PA = PD二AB = DC二a，因为/ APD= 90 ，所以PAD为等腰直角三角形即AD= , 2a取AD中点E，连接PE，则PE a , PE _ AD .2又因为平面PAB —平面PAD所以PE _平面ABCD 且两圆锥的顶因为AB丄平面PAD , AB // CD所以AB — AD , CD —AD又AB 二DC =a所以四边形ABCD为矩形所以V P^BCD J/BADpE 2a=[a3=8所以 3 3 2 3 3即a = 211 一S侧= 2 2 3+ 2 . 26=6+2 .32 2【2016, 18】如图所示，已知正三棱锥P - ABC的侧面是直角三角形，PA = 6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E •连结PE并延长交AB于点G .(1)求证：G是AB的中点；2)在题图中作出点E在平面PAC内的正投影F (说明作法及理由)，并求四面体PDEF的体积.解析：(1)由题意可得△ ABC为正三角形，故PA = PB=PC=6. 因为P在平面ABC内的正投影为点D，故PD —平面ABC • 又AB 平面ABC，所以AB _ PD .因为D在平面PAB内的正投影为点E ,故DE _平面PAB .又AB 平面PAB，所以AB _ DE .因为AB _ PD , AB _ DE , PD「| DE 二D , PD, DE 平面PDG , 所以AB _平面PDG •又PG 平面PDG，所以AB _ PG .因为PA二PB，所以G是AB的中点.(2)过E作EF // BP交PA于F，则F即为所要寻找的正投影.理由如下，因为 PB _ PA , PB// EF ，故EF _ PA •同理EF _ PC , 又 PA n PC = P , PA,PC 平面 PAC ，所以 EF _ 平面 PAC , 故F 即为点E 在平面PAC 内的正投影.11所以 V D _PEFS A PEF DE PF EF DE . 3 6在厶PDG 中，PG =3.2 , DG=、、6 , PD =2；3，故由等面积法知 DE =2 .由勾股定理知PE 二2、、2，由△ PEF 为等腰直角三角形知 PF =EF =2，故V D 』EF【2015, 18】如图四边形 ABCD^菱形，G 为AC 与 BD 交点,(I )证明：平面 AEC L 平面BED(n )若/ ABC 120°, AEL EC 三棱锥 E- ACD解：(I ) •/ BEL 平面 ABCD ： BEL AC•/ ABCD^ 菱形，••• BD L AC••• ACL 平面BED 又AC 平面AEC •平面 AECL 平面 (n )设 AB=x 在菱形 ABCD^，由/ AB(=120° 可得，AG=GC=3 X在 Rt △ AEC 中，可得 EG=22由 BA=BD=B 可得 AE= ED=EC=6 .•••△ AEC 的面积为3,A EAD 勺面积与厶ECD 勺面积均为,5 .C所以三棱锥E-ACD 勺侧面积为3+2- 5 .…12分的体积为—，求该三棱锥的侧面积.3•••在Rt △ EBG 为直角三角形，可得BE=l x .2…V E /CD1AC GD BE 6x 3224解得x =2 .18.解析 (1)因为BE _平面ABCD，所以BE _ AC . 又ABCD为菱形，所以AC _ BD .又因为BD^BE B , BD , BE 二平面BED ,所以AC —平面BED .又AC二平面AEC，所以平面AEC _平面BED .(2)在菱形ABCD 中，取AB 二BC 二CD 二AD 二2x ,又ABC = 120，所以AG 二GC =：；3x，BG 二GD = x .在厶AEC 中，AEC=90_，所以EG AC 〜3x ,2所以在Rt △ EBG 中，BE h：$EG2 - BG2「hm2x ,所以V EJkCD =- - 2x 2x sin120：'迈x 6x3 6，解得x=1.3 2 3 3在Rt△ EBA , Rt△ EBC , Rt△ EBD 中，可得AE 二EC 二ED 二6 .1 1 J—所以三棱锥的侧面积S侧二2 2 6 、6 = 3 • 2、5.2 2【2014,19】如图，三棱柱ABC-ABQ中，侧面BB1C1C为菱形，B1C的中点为O，且AO _平(2)若AC _ AB, CBB^ =60 ,BC =1,求三棱柱ABC-ABG 的高.证明：(I )连接BC,则O为BC与BC的交点，••• AC L平面BBCC.二AOL BC, …2 分因为侧面BBGC为菱形，••• BG丄BC,-4分••• BG丄平面ABC，：AB 平面ABC,故BC丄AB …6分(II)作ODL BC 垂足为D,连结AD ••• AOL BC,二BC丄平面AOD 又BC平面ABC二平面ABCL 平面AOD交线为AD,作OH L AD,垂足为H ,二OH L平面ABC …9分•••/ CBB=60°,所以△ CBB为等边三角形,又BC=1 ,可得O[= '3,41 1 t面BB C C .(1)证明：BQ _ AB;由于AC L AB , ••• OA B1C ,二AD h^OD2 OA22 2由OHAD=ODOA 可得OH=W ，又0为BC 的中点，所以点B 到平面ABC 的距离为 1 ,14 7所以三棱柱ABC-ABG 的高高为。

2011年—2018年新课标全国卷(1卷、2卷、3卷)文科数学试题分类汇编—8.三角函数、解三角形2011年—2018年新课标全国卷Ⅰ文科数学分类汇编7.三角函数、解三角形一、选择题2018年新课标Ⅰ文8题：已知函数$f(x)=2\cos x-\sin x+2$，则$f(x)$的最小正周期为$\pi$，最大值为3.2018年新课标Ⅰ文11题：已知角$\alpha$的顶点为坐标原点，始边与$x$轴的非负半轴重合，终边上有两点$A(1,0)$，$B(2,b)$，且$\cos2\alpha=\frac{1}{5}$，则$a-b=\frac{1}{5}$。

2018年新课标Ⅱ文7题：在$\triangle ABC$中，$\cos C=\frac{5}{\sqrt{26}}$，$BC=1$，$AC=5$，则$AB=5\sqrt{2}$。

2018年新课标Ⅱ文10题：若$f(x)=\cos x-\sin x$在$[0,a]$是减函数，则$a$的最大值是$\frac{3\pi}{4}$。

2018年新课标Ⅲ文4题：若$\sin \alpha=\frac{1}{\sqrt{8}}$，则$\cos 2\alpha=-\frac{7}{8}$。

2018年新课标Ⅲ文6题：函数$f(x)=\frac{\tan x}{1+\tan^2 x}$的最小正周期为$\pi$。

2018年新课标Ⅲ文11题：triangle ABC$的内角$A$，$B$，$C$的对边分别为$a$，$b$，$c$。

若$\triangle ABC$的面积为$4$，则$\cosC=\frac{3}{4}$。

2017年新课标Ⅰ文11题：triangle ABC$的内角$A$、$B$、$C$的对边分别为$a$、$b$、$c$。

已知$\sin B+\sin A(\sin C-\cos C)=\frac{3}{2}$，$a=2$，$c=2$，则$C=\frac{\pi}{3}$。

《2018年高考文科数学分类汇编》、选择题1.【2018全国一卷7】在厶ABC 中，AD 为BC 边上的中线,D .押 4A C2 .【2018全国二卷4】已知向量a , b 满足|a | =1 , a b = -1，则a (2a-b )二n4.【2018浙江卷9】已知a, b, e 是平面向量，e 是单位向量.若非零向量a 与e 的夹角为-， 3 向量b 满足b 2- 4e - b +3=0，则|a - b |的最小值是、填空题 1.【2018全国三卷13】已知向量a = 1,2 , b = 2, -2 , c = 1,入.若c // 2a+b ，则■二2. ___________________________________________________________________________ 【2018 北京卷 9】设向量 a = (1,0) , b = (- 1,m )若 a - (m a -b )，贝V m= __________________3. 【2018江苏卷12】在平面直角坐标系 xOy 中，A 为直线I : y = 2x 上在第一象限内的点，T TB(5,0)，以AB 为直径的圆C 与直线l 交于另一点D .若AB CD = 0，则点A 的横坐标为 _______ .第五篇：平面向量A . 3AB 一1 AC 4 4 E 为AD 的中点，则B . 3C . 2D . 03.【2018天津卷8】在如图的平面图形中，已知 OM =1 , ON =2 , MON=120 , BM = 2MA,CN =2NA,则的值为A. -15B.-9C.-6D.0B . 3+1C . 24. 【2018上海卷8】在平面直角坐标系中，已知点 A (-1 , 0), B (2, 0), E, F是y轴上的两个动点，且I存i=2，贝y AE• BF的最小值为 ______ [参考答案一、选择题1.A2.B二、填空题11.2 3.C 4.A2. -13.34.一3。

2011—2019年高考真题全国卷1理科数学分类汇编——5.平面向量一、选择题【2019，7】已知非零向量,a b r r 满足2a b =r r ，且()a b b -⊥r r r ，则a r 与b r 的夹角为（ ）A.6π B.3π C.23π D.56π 【2018，6】在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB =u u u r （ ）A ．3144AB AC -u u u r u u u r B ．1344AB AC -u u u r u u u r C ．3144AB AC +u u u r u u u rD ．1344AB AC +u u u r u u u r 【2015，7】设D 为ABC ∆错误!未找到引用源。

所在平面内一点3BC CD =u u u r u u u r ，则（ ）A ．1433AD AB AC =-+u u u r u u u r u u u r B ．1433AD AB AC =-u u u r u u u r u u u r C ．4133AD AB AC =+u u u r u u u r u u u r D ．4133AD AB AC =-u u u r u u u r u u u r 【2011，10】已知a 与b 均为单位向量，其夹角为θ，有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈ ⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦ 其中的真命题是（ ）A ．14,P PB ．13,P PC ．23,P PD ．24,P P二、填空题【2017，13】已知向量a ，b 的夹角为60°，|a |=2， | b |=1，则| a +2 b |= ．【2016，13】设向量a )1,(m =，b )2,1(=，且|a +b ||2=a ||2+b 2|，则=m ．【2014，15】已知A ，B ，C 是圆O 上的三点，若1()2AO AB AC =+u u u r u u u r u u u r ，则AB u u u r 与AC uuu r 的夹角为 ． 【2013，13】已知两个单位向量a ，b 的夹角为60°，c ＝t a ＋(1－t )b ．若b ·c ＝0，则t ＝__________．【2012，13】已知向量a r ，b r 夹角为45°，且||1a =r ，|2|10a b -=r r ||b =r _________．5．平面向量（解析版）一、选择题【2019，7】已知非零向量,a b r r 满足2a b =r r ，且()a b b -⊥r r r ，则a r 与b r 的夹角为（ ）A.6π B.3π C.23π D.56π 【解析】设a r 与b r 的夹角为θ，∵()a b b -⊥r r r ∴2()cos a b b a b b θ-⋅=-r r r r r r =0∴1cos =2θ ∴=3πθ.选B【2018，6】在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB =u u u r （ ）A ．3144AB AC -uu u r uu u r B ．1344AB AC -u u u r u u u r C ．3144AB AC +u u u r u u u r D ．1344AB AC +u u u r u u u r【解析】选A【2015，7】设D 为ABC ∆错误!未找到引用源。

2011年—2018年新课标全国卷文科数学分类汇编11．解析几何一、选择题(2018·新课标Ⅰ，文4)已知椭圆C ：22214x y a +=的一个焦点为(20)，，则C 的离心率为（）A ．13B ．12C ．22D ．223(2018·新课标Ⅱ，文6)双曲线22221(0,0)x y a b a b-=>>的离心率为）A ．y =B ．y =C ．y x =D ．y =(2018·新课标Ⅱ，文11)已知1F ，2F 是椭圆C 的两个焦点，P 是C 上的一点，若12PF PF ⊥，且2160PF F ∠=︒，则C 的离心率为（）A ．312-B ．2C ．312D 1-(2018·新课标Ⅲ，文8)直线20x y ++=分别与x 轴，y 轴交于A ，B 两点，点P 在圆()2222x y -+=上，则ABP ∆面积的取值范围是（）A ．[]26，B ．[]48，C ．D ．⎡⎣(2018·新课标Ⅲ，文10)已知双曲线22221x y C a b-=：（00a b >>，，则点()40，到C 的渐近线的距离为（）A B ．2C ．322D ．(2017·新课标Ⅰ，文5)已知F 是双曲线22:13y C x -=的右焦点，P 是C 上一点，且PF 与x 轴垂直，点A 的坐标是(1,3)，则APF ∆的面积为（）A ．13B ．12C ．23D ．32(2017·新课标Ⅰ，文12)设A 、B 是椭圆C ：2213x y m+=长轴的两个端点，若C 上存在点M 满足∠AMB =120°，则m 的取值范围是()A ．(0,1][9,)+∞ B ．[9,)+∞ C ．(0,1][4,)+∞ D ．[4,)+∞ （2017·新课标Ⅱ，文5）若a ＞1，则双曲线2221-=x y a的离心率的取值范围是（）A.+∞）B.2）C. D.12（，）（2017·新课标Ⅱ，文12）过抛物线C ：y 2=4x 的焦点F ，C 于点M （M 在x 轴上方），l 为N 在MN ⊥l,则M NF ）A. B. C. D.(2017·新课标Ⅲ，文11)已知椭圆()2222:10x y C a b a b+=>>的左、右顶点分别为1A ，2A ，且以线段12A A 为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为（）A ．3B ．3C ．3D ．13(2016·新课标Ⅰ，文5)直线l 经过椭圆的一个顶点和一个焦点，若椭圆中心到l 的距离为其短轴长的14，则该椭圆的离心率为（）A ．13B ．12C ．23D ．34（2016·新课标Ⅱ，文5）设F 为抛物线C ：y 2=4x 的焦点，曲线y =kx(k >0)与C 交于点P ，PF ⊥x 轴，则k =A ．12B ．1C ．32D ．2（2016·新课标Ⅱ，文6）圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1，则a =（）A ．43-B ．34-C D ．2(2016·新课标Ⅲ，文12)已知O 为坐标原点，F 是椭圆2222:1(0)x y C a b a b+=>>的左焦点，A ，B 分别为C 的左，右顶点．P 为C 上一点，且PF x ⊥轴．过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E ．若直线BM 经过OE 的中点，则C 的离心率为()．A ．13B ．12C ．23D ．34(2015·新课标Ⅰ，文5)已知椭圆E 的中心为坐标原点，离心率为12，E 的右焦点与抛物线C :y 2=8x ，的焦点重合，A ,B 是C 的准线与E 的两个交点，则|AB |=()A ．3B ．6C ．9D ．12（2015·新课标Ⅱ，文7）已知三点)0,1(A ，)3,0(B ，)3,2(C ，则ABC ∆外接圆的圆心到原点的距离为A.53B.C.D.43(2014·新课标Ⅰ，文10)已知抛物线C ：y 2=x 的焦点为F ，A (x 0,y 0)是C 上一点，|AF |=054x ，则x 0=()A ．1B ．2C ．4D ．8(2014·新课标Ⅰ，文4)已知双曲线)0(13222>=-a y a x 的离心率为2，则a=()A ．2B ．26C ．25D ．1（2014·新课标Ⅱ，文10）设F 为抛物线C ：y 2=3x 的焦点，过F 且倾斜角为30°的直线交于C 于A 、B 两点，则|AB |=（）A B ．6C ．12D ．（2014·新课标Ⅱ，文12）设点M (x 0，1)，若在圆O ：x 2+y 2=1上存在点N ，使得∠OMN =45°，则x 0的取值范围是（）A ．[1,1]-B ．11[]22-，C ．[D ．[(2013·新课标Ⅰ，文4)已知双曲线C ：2222=1x y a b-(a ＞0，b ＞0)的离心率为52，则C 的渐近线方程为()A ．y ＝14x ±B ．y ＝13x ±C ．y ＝12x ±D ．y ＝±x(2013·新课标Ⅰ，文8)O 为坐标原点，F 为抛物线C ：y 2＝的焦点，P 为C 上一点，若|PF |＝则△POF 的面积为()A ．2B ．C ．D ．4（2013·新课标Ⅱ，文5）设椭圆2222:1x y C a b +=(0)a b >>的左、右焦点分别为12,F F ，P 是C 上的点，212PF F F ⊥，1230PF F ∠=，则C 的离心率为（）A ．6B ．13C ．12D ．3（2013·新课标Ⅱ，文10）设抛物线C :y 2=4x 的焦点为F ，直线l 过F 且与C 交于A ，B 两点.若|AF |=3|BF |，则l 的方程为（）A ．1y x =-或1yx =-+B ．(1)3y x =-或(1)3y x =--C ．1)y x =-或1)y x =-D ．(1)2y x =-或(1)2y x =--(2012·新课标Ⅰ，文4)设1F 、2F 是椭圆E ：2222x y a b +（0a b >>）的左、右焦点，P 为直线32ax =上一点，21F PF ∆是底角为30°的等腰三角形，则E 的离心率为（）A ．12B ．23C ．34D ．45(2012·新课标Ⅰ，文10)等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线216y x =的准线交于A ，B 两点，||AB =，则C 的实轴长为（）A B ．C ．4D ．8(2011·新课标Ⅰ，文4)椭圆221168x y +=的离心率为（）A ．13B ．12C ．3D ．2(2011·新课标Ⅰ，文9)已知直线l 过抛物线的焦点，且与C 的对称轴垂直，l 与C 交于A ，B 两点，12AB =，P 为C 的准线上一点，则ABP △的面积为（）．A ．18B ．24C ．36D ．48二、填空题(2018·新课标Ⅰ，文15)直线1y x =+与圆22230x y y ++-=交于A ，B 两点，则||AB =.(2016·新课标Ⅰ，文15)设直线2y x a =+与圆22:220C x y ay +--=相交于,A B 两点，若AB =，则圆C 的面积为．(2016·新课标Ⅲ，文15)已知直线:60l x -+=与圆2212x y +=交于A 、B 两点，过A 、B 分别作l的垂线与x 轴交于C 、D 两点，则CD =_________．(2015·新课标Ⅰ，文16)已知F 是双曲线C :2218y x -=的右焦点，P 是C 左支上一点，A ，当ΔAPF 周长最小时，该三角形的面积为．（2015·新课标Ⅱ，文15）已知双曲线过点，且渐近线方程为12y x =±，则该双曲线的标准方程为.三、解答题(2018·新课标Ⅰ，文20)设抛物线2:2C y x =，点()2,0A ，()2,0B -，过点A 的直线l 与C 交于M ，N两点.（1）当l 与x 轴垂直时，求直线BM 的方程；（2）证明：ABM ABN ∠=∠.(2018·新课标Ⅱ，文20)设抛物线24C y x =：的焦点为F ，过F 且斜率为(0)k k >的直线l 与C 交于A ，B 两点，||8AB =．（1）求l 的方程；（2）求过点A ，B 且与C 的准线相切的圆的方程．(2018·新课标Ⅲ，文20)已知斜率为k 的直线l 与椭圆22143x y C +=：交于A ，B 两点．线段AB 的中点为()()10M m m >，．（1）明：12k <-；⑵设F 为C 的右焦点，P 为C 上一点,且0FP FA FB ++= ．证明:2FP FA FB =+ ．(2017·新课标Ⅰ，文20)设A ，B 为曲线C ：24x y =上两点，A 与B 的横坐标之和为4．（1）求直线AB 的斜率；（2）设M 为曲线C 上一点，C 在M 处的切线与直线AB 平行，且BM AM ⊥，求直线AB 的方程．（2017·新课标Ⅱ，文20）设O 为坐标原点，动点M 在椭圆C ：2212x y +=上，过M 作x 轴的垂线，垂足为N ，点P 满足NP =（1）求点P 的轨迹方程；（2）设点Q 在直线x =-3上，且1OP PQ ⋅=.证明过点P 且垂直于OQ 的直线l 过C 的左焦点F.(2017·新课标Ⅲ，文20)在直角坐标系xOy 中，曲线2–2y x mx =+与x 轴交于A ，B 两点，点C 的坐标为()01，．当m 变化时，解答下列问题：（1）能否出现AC BC ⊥的情况？说明理由；（2）证明过A ，B ，C 三点的圆在y 轴上截得的弦长为定值．(2016·新课标Ⅰ，文20)在直角坐标系xOy 中，直线:(0)l y t t =≠交y 轴于点M ，交抛物线2:2(0)C y px p =>于点P ，M 关于点P 的对称点为N ，连结ON 并延长交C 于点H ．（1）求OHON；（2）除H 以外，直线MH 与C 是否有其他公共点？请说明理由．（2016·新课标Ⅱ，文21）已知A 是椭圆E :22143x y +=的左顶点，斜率为k (k >0)的直线交E 于A ，M 两点，点N 在E 上，MA ⊥NA .（Ⅰ）当|AM|=|AN|时，求△AMN 的面积；（Ⅱ）当|AM|=|AN|2k <<.(2016·新课标Ⅲ，文20)已知抛物线2:2C y x =的焦点为F ，平行于x 轴的两条直线1l ，2l 分别交C 于A ，B 两点，交C 的准线于P ，Q 两点．（1）若F 在线段AB 上，R 是PQ 的中点，证明//AR FQ ；（2）若PQF △的面积是ABF △的面积的两倍，求AB 中点的轨迹方程．(2015·新课标Ⅰ，文20)已知过点A (0,1)且斜率为k 的直线l 与圆C ：(x -2)2+(y -3)2=1交于M ,N 两点.(Ⅰ)求k 的取值范围；(Ⅱ)OM ON ⋅=12，其中O 为坐标原点，求|MN |.（2015·新课标Ⅱ，文20）已知椭圆C ：22221x y a b +=（a >b >0）的离心率为2，点（2）在C 上.（Ⅰ）求C 的方程；（Ⅱ）直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A 、B ，线段AB 的中点为M ，证明：直线OM 的斜率与直线l 的斜率的乘积为定值.(2014·新课标Ⅰ，文20)已知点)2,2(P ，圆C :0822=-+y y x ，过点P 的动直线l 与圆C 交于B A ,两点，线段AB 的中点为M ，O 为坐标原点.(1)求M 的轨迹方程；(2)当OM OP =时，求l 的方程及POM ∆的面积.（2014·新课标Ⅱ，文20）设F 1，F 2分别是椭圆C ：12222=+by a x （a >b >0）的左、右焦点，M 是C 上一点且MF 2与x 轴垂直，直线MF 1与C 的另一个交点为N .（Ⅰ）若直线MN 的斜率为43，求C 的离心率；（Ⅱ）若直线MN 在y 轴上的截距为2且|MN |=5|F 1N |，求a ，b .(2013·新课标Ⅰ，文21)已知圆M ：(x ＋1)2＋y 2＝1，圆N ：(x －1)2＋y 2＝9，动圆P 与圆M 外切并且与圆N 内切，圆心P 的轨迹为曲线C .(1)求C 的方程；(2)l 是与圆P ，圆M 都相切的一条直线，l 与曲线C 交于A ，B 两点，当圆P 的半径最长时，求|AB |.（2013·新课标Ⅱ，文20）在平面直角坐标系xoy 中，已知圆P 在x 轴上截得线段长为y 轴上截得线段长为（Ⅰ）求圆心P 的轨迹方程；（Ⅱ）若P 点到直线y x =的距离为22，求圆P 的方程.(2012·新课标Ⅰ，文20)设抛物线C ：py x 22=（0>p ）的焦点为F ，准线为l ，A 为C 上一点，已知以F 为圆心，FA 为半径的圆F 交l 于B ，D 两点。

2011年—2018年新课标全国卷文科数学分类汇编9．数列一、选择题(2015·新课标Ⅰ，文7)已知{a n }是公差为1的等差数列，S n 为{a n }的前n 项和，若S 8=4S 4，则a 10=()A ．172B ．192C ．10D ．12（2015·新课标Ⅱ，文5）设n S 是等差数列}{n a 的前n 项和，若3531=++a a a ，则=5S （）A.5B.7C.9D.11（2015·新课标Ⅱ，文9）已知等比数列}{n a 满足411=a ，)1(4453-=a a a ，则=2a （）A.2B.1C.21 D.81（2014·新课标Ⅱ，文5）等差数列{a n }的公差为2，若a 2，a 4，a 8成等比数列，则{a n }的前n 项S n =（）A ．(1)n n +B ．(1)n n -C ．(1)2n n +D ．(1)2n n -(2013·新课标Ⅰ，文6)设首项为1，公比为23的等比数列{a n }的前n 项和为S n ，则()．A ．S n ＝2a n －1B ．S n ＝3a n －2C ．S n ＝4－3a nD ．S n ＝3－2a n(2012·新课标Ⅰ，文12)数列{n a }满足1(1)21n n n a a n ++-=-，则{n a }的前60项和为（）A ．3690B ．3660C ．1845D ．1830二、填空题(2015·新课标Ⅰ，文13)数列{a n }中，a 1=2，a n +1=2a n ，S n 为{a n }的前n 项和，若S n =126，则n =．（2014·新课标Ⅱ，文16）数列}{n a 满足nn a a -=+111，2a =2，则1a =_________.(2012·新课标Ⅰ，文14)等比数列{}n a 的前n 项和为n S ，若3230S S +=，则公比q =_____．三、解答题(2018·新课标Ⅰ，文17)已知数列{}n a 满足11a =，()121n n na n a +=+，设nn a b n=．（1）求123b b b ，，；（2）判断数列{}n b 是否为等比数列，并说明理由；（3）求{}n a 的通项公式．(2018·新课标Ⅱ，文17)记n S 为等差数列{}n a 的前n 项和，已知17a =-，315S =-．（1）求{}n a 的通项公式；（2）求n S ，并求n S 的最小值．(2018·新课标Ⅲ，文17)等比数列{}n a 中，15314a a a ==，．（1）{}n a 的通项公式；⑵记n S 为{}n a 的前n 项和．若63m S =，求m ．(2017·新课标Ⅰ，文17)记n S 为等比数列{}n a 的前n 项和，已知22S =,36S =-．（1）求{}n a 的通项公式；（2）求n S ，并判断1n S +，n S ，2n S +是否成等差数列．（2017·新课标Ⅱ，文17）已知等差数列{a n }的前n 项和为S n ，等比数列{b n }的前n 项和为T n ，a 1=-1，b 1=1，a 2+b 2=2.（1）若a 3+b 3=5，求{b n }的通项公式；（2）若T 3=21，求S 3.(2017·新课标Ⅲ，文17)设数列{}n a 满足()123212n a a n a n +++-= ．（1）求{}n a 的通项公式；（2）求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和．(2016·新课标Ⅰ，文17)已知{}n a 是公差为3的等差数列，数列{}n b 满足12111==3n n n n b b a b b nb +++=1，，．（1）求{}n a 的通项公式；（2）求{}n b 的前n 项和．（2016·新课标Ⅱ，文17）等差数列{a n }中，a 3+a 4=4，a 5+a 7=6．（Ⅰ）求{a n }的通项公式；（Ⅱ）设b n =[lg a n ]，求数列{b n }的前10项和，其中[x ]表示不超过x 的最大整数，如[0.9]=0，[2.6]=2.(2016·新课标Ⅲ，文17)已知各项都为正数的数列{}n a 满足11a =，211(21)20n n n n a a a a ++---=．（1）求23,a a ；（2）求{}n a 的通项公式．(2014·新课标Ⅰ，文17)已知{}n a 是递增的等差数列，2a ，4a 是方程2560x x -+=的根。

2018年全国高考文科数学分类汇编——平面向量1.（浙江）已知，，是平面向量，是单位向量．若非零向量与的夹角为，向量满足﹣4•+3=0，则|﹣|的最小值是（）AA．﹣1 B．+1 C．2 D．2﹣【解答】解：由﹣4•+3=0，得，∴（）⊥（），如图，不妨设，则的终点在以（2，0）为圆心，以1为半径的圆周上，又非零向量与的夹角为，则的终点在不含端点O的两条射线y=（x＞0）上．不妨以y=为例，则|﹣|的最小值是（2，0）到直线的距离减1．即．故选：A．2. （天津）在如图的平面图形中，已知OM=1，ON=2，∠MON=120°，=2，=2，则的值为（）CA．﹣15 B．﹣9 C．﹣6 D．0【解答】解：不妨设四边形OMAN是平行四边形，由OM=1，ON=2，∠MON=120°，=2，=2，知=﹣=3﹣3=﹣3+3，∴=（﹣3+3）•=﹣3+3•=﹣3×12+3×2×1×cos120°=﹣6．故选：C．3. （上海）在平面直角坐标系中，已知点A （﹣1，0）、B （2，0），E 、F 是y 轴上的两个动点，且||=2，则的最小值为 ﹣3 ． 【解答】解：根据题意，设E （0，a ），F （0，b ）； ∴； ∴a=b +2，或b=a +2； 且； ∴； 当a=b +2时，； ∵b 2+2b ﹣2的最小值为； ∴的最小值为﹣3，同理求出b=a +2时，的最小值为﹣3． 故答案为：﹣3．4. （全国3卷）已知向量(1,2)=a ，(2,2)=-b ，(1,)λ=c ．若()2+c a b ，则λ=________．【解答】解：∵向量=（1，2），=（2，﹣2），∴=（4，2）， ∵=（1，λ），∥（2+），∴，解得λ=．故答案为：．5. （全国2卷）已知向量，满足||=1，=﹣1，则•（2）=（ ）B A ．4 B ．3 C ．2 D ．0【解答】解：向量，满足||=1，=﹣1，则•（2）=2﹣=2+1=3，故选：B ． 6. 在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则=（ ）AA ．﹣B ．﹣C ．+D ．+【解答】解：在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，=﹣=﹣ =﹣×（+）=﹣，故选：A ．7.（江苏）在平面直角坐标系xOy中，A为直线l：y=2x上在第一象限内的点，B（5，0），以AB为直径的圆C与直线l交于另一点D．若=0，则点A的横坐标为3．【解答】解：设A（a，2a），a＞0，∵B（5，0），∴C（，a），则圆C的方程为（x﹣5）（x﹣a）+y（y﹣2a）=0．联立，解得D（1，2）．∴=．解得：a=3或a=﹣1．又a＞0，∴a=3．即A的横坐标为3．故答案为：3．8. （北京）设向量=（1，0），=（﹣1，m）．若⊥（m﹣），则m=﹣1．【解答】解：向量=（1，0），=（﹣1，m）．m﹣=（m+1，﹣m）．∵⊥（m﹣），∴m+1=0，解得m=﹣1．故答案为：﹣1．。

一、选择题【2015，7】设D 为ABC ∆所在平面内一点3BC CD =，则（ ）A ．1433AD AB AC =-+ B ．1433AD AB AC =- C ．4133AD AB AC =+ D ．4133AD AB AC =- 【2011，10】已知a 与b 均为单位向量，其夹角为θ，有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈ ⎥⎝⎦ 3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是（ ）A ．14,P PB ．13,P PC ．23,P PD ．24,P P二、填空题【2017，13】已知向量a ，b 的夹角为60°，|a |=2， | b |=1，则| a +2 b |= ．【2016，13】设向量a )1,(m =，b )2,1(=，且|a +b ||2=a ||2+b 2|，则=m ．【2014，15】已知A ，B ，C 是圆O 上的三点，若1()2AO AB AC =+，则AB 与AC 的夹角为 ． 【2013，13】已知两个单位向量a ，b 的夹角为60°，c ＝t a ＋(1－t )b ．若b ·c ＝0，则t ＝__________．【2012，13】已知向量a ，b 夹角为45°，且||1a =，|2|10a b -=，则||b =_________．一、选择题【2015，7】设D 为ABC ∆所在平面内一点3BC CD =，则（ ）A ．1433AD AB AC =-+ B ．1433AD AB AC =- C ．4133AD AB AC =+ D ．4133AD AB AC =- 解析：11()33AD AC CD AC BC AC AC AB =+=+=+-=1433AB AC -+，选A ．. 【2011，10】已知a 与b 均为单位向量，其夹角为θ，有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈ ⎥⎝⎦ 3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是（ ）A ．14,P PB ．13,P PC ．23,P PD ．24,P P解析：1a b +==>得， 1cos 2θ>-，20,3πθ⎡⎫⇒∈⎪⎢⎣⎭．由1a b -==>得1cos 2θ<，,3πθπ⎛⎤⇒∈ ⎥⎝⎦． 选A ． 二、填空题 【2017，13】已知向量a ，b 的夹角为60°，|a |=2， | b |=1，则| a +2 b |= ． 【解析】()22222(2)22cos602a b a b a a b b+=+=+⋅⋅⋅︒+221222222=+⨯⨯⨯+444=++12=，∴212a b += 【法二】令2,c b =由题意得，2a c ==，且夹角为60，所以2a b a c +=+的几何意义为以,a c 夹角为60的平行四边形的对角线所在的向量，易得223a b a c +=+=；【2016，13】设向量a )1,(m =，b )2,1(=，且|a +b ||2=a ||2+b 2|，则=m ．【解析】由已知得：()1,3a b m +=+，∴()22222222213112a b a b m m +=+⇔++=+++，解得2m =-． 【2014，15】已知A ，B ，C 是圆O 上的三点，若1()2AO AB AC =+，则AB 与AC 的夹角为 .【解析】∵1()2AO AB AC =+，∴O 为线段BC 中点，故BC 为O 的直径，∴090BAC ∠=，∴AB 与AC 的夹角为090．【2013，13】已知两个单位向量a ，b 的夹角为60°，c ＝t a ＋(1－t )b .若b ·c ＝0，则t ＝__________.解析：∵c ＝t a ＋(1－t )b ，∴b ·c ＝t a ·b ＋(1－t )|b |2，又∵|a |＝|b |＝1，且a 与b 夹角为60°，b ⊥c ，∴0＝t |a ||b |cos 60°＋(1－t )，0＝12t ＋1－t ，∴ t ＝2. 【2012，13】已知向量a ，b 夹角为45°，且||1a =，|2|10a b -=，则||b =_________． 【解析】由已知||2245cos ||||=︒⋅⋅=⋅，因为|2|10a b -=，所以10||4||422=+⋅-， 即06||22||2=--b b ， 解得23||=b ．。

5．平面向量（含解析）一、选择题【2018,7】在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB =A ．3144AB AC - B ．1344AB AC - C ．3144AB AC + D ．1344AB AC + 【2015，2】2．已知点A (0,1)，B (3,2)，向量(4,3)AC =--，则向量BC =( )A ．(-7,-4)B ．(7,4)C ．(-1,4)D ．(1,4)【2014，6】设D ,E ,F 分别为ΔABC 的三边BC ,CA ,AB 的中点，则=+( )A ．ADB ．AD 21 C ．BC 21 D ．BC 二、填空题 【2017，13】已知向量()1,2a =-，(),1b m =，若向量a b +与a 垂直，则m = ．【2016，13】设向量()1x x +,a =，()12,b =，且⊥a b ，则x = ．【2013，13】已知两个单位向量a ，b 的夹角为60°，c ＝ta ＋(1－t )b ．若b ·c ＝0，则t ＝______．【2012，15】15．已知向量a ，b 夹角为45°，且||1a =，|2|10a b -=，则||b =_________．【2011，13】 已知a 与b 为两个不共线的单位向量，k 为实数，若向量+a b 与向量k -a b 垂直，则k = ．5．平面向量（解析版）一、选择题【2018,7】在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB =A ．3144AB AC - B ．1344AB AC - C ．3144AB AC + D ．1344AB AC + 解：2121+=+= )(21)(2121-++⨯⨯=4143-= 故选A 【2015，2】2．已知点A (0,1)，B (3,2)，向量(4,3)AC =--，则向量BC =( )A ．(-7,-4)B ．(7,4)C ．(-1,4)D ．(1,4)解：(3,1),AB BC AC AB =∴=-=(-7,-4)，故选A【2014，6】设D ,E ,F 分别为ΔABC 的三边BC ,CA ,AB 的中点，则=+( )A ．B ．21 C ．21 D ． 解：+EB FC EC CB FB BC +=++=111()222AC AB AB AC AD +=+=,故选A 二、填空题【2017，13】已知向量()1,2a =-，(),1b m =，若向量a b +与a 垂直，则m = ．【解析】由题得(1,3)a b m +=-，因为()0a b a +⋅=，所以(1)230m --+⨯=，解得7m =；【2016，13】设向量()1x x +,a =，()12,b =，且⊥a b ，则x = ． 解析：23-．由题意()210x x ⋅=++=a b ，解得23x =-．故填23-． 【2013，13】已知两个单位向量a ，b 的夹角为60°，c ＝ta ＋(1－t )b ．若b ·c ＝0，则t ＝______． 解析：2． ∵b ·c ＝0，|a |＝|b |＝1，〈a ，b 〉＝60°，∴a ·b ＝111122⨯⨯=． ∴b ·c ＝[ta ＋(1－t )b ]·b ＝0，即ta ·b ＋(1－t )b 2＝0．∴12t ＋1－t ＝0． ∴t ＝2． 【2012，15】15．已知向量a ，b 夹角为45°，且||1a =，|2|10a b -=，则||b =_________．【解析】23． 由已知||2245cos ||||=︒⋅⋅=⋅． 因为|2|10a b -=，所以10||4||422=+⋅-b b a a ，即06||22||2=--b b ， 解得23||=b ．【2011，13】 已知a 与b 为两个不共线的单位向量，k 为实数，若向量+a b 与向量k -a b 垂直，则k = ． 【解析】因为a 与b 为两个不共线的单位向量，所以1==a b ．又k -a b 与+a b 垂直，所以()()0k +⋅-=a b a b ，即220k k +⋅-⋅-=a a b a b b ，所以10k k -+⋅-⋅=a b a b ，即1cos cos 0k k θθ-+-=．（θ为a 与b 的夹角）所以()()11cos 0k θ-+=，又a 与b 不共线，所以cos 1θ≠-，所以1k =．故答案为1．。

F 单元 平面向量F1 平面向量的概念及其线性运算7.F1[2018·全国卷Ⅰ] 在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB⃗⃗⃗⃗⃗ = ( )A . 34AB ⃗⃗⃗⃗⃗ -14AC ⃗⃗⃗⃗⃗ B . 14AB ⃗⃗⃗⃗⃗ -34AC ⃗⃗⃗⃗⃗ C . 34AB ⃗⃗⃗⃗⃗ +14AC ⃗⃗⃗⃗⃗ D . 14AB ⃗⃗⃗⃗⃗ +34AC ⃗⃗⃗⃗⃗ 7.A [解析] 如图,EB ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ -AE ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ -12AD ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ -12×12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )=34AB ⃗⃗⃗⃗⃗ -14AC ⃗⃗⃗⃗⃗ ,故选A .8.F1、F3[2018·天津卷]在如图1-2的平面图形中,已知OM=1,ON=2,∠MON=120°,BM ⃗⃗⃗⃗⃗⃗ =2MA ⃗⃗⃗⃗⃗⃗ ,CN ⃗⃗⃗⃗⃗ =2NA ⃗⃗⃗⃗⃗⃗ ,则BC ⃗⃗⃗⃗⃗ ·OM⃗⃗⃗⃗⃗⃗ 的值为 ( )图1-2A .-15B . -9C . -6D . 08.C [解析] 连接MN ,由BM ⃗⃗⃗⃗⃗⃗ =2MA ⃗⃗⃗⃗⃗⃗ ,CN ⃗⃗⃗⃗⃗ =2NA ⃗⃗⃗⃗⃗⃗ ,可得MN ∥BC ,且BC=3MN ,所以BC ⃗⃗⃗⃗⃗ =3MN ⃗⃗⃗⃗⃗⃗⃗ ,所以BC ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ =3MN ⃗⃗⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ =3(ON ⃗⃗⃗⃗⃗⃗ -OM ⃗⃗⃗⃗⃗⃗ )·OM ⃗⃗⃗⃗⃗⃗ =3(ON ⃗⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ -OM ⃗⃗⃗⃗⃗⃗ 2)=3×(1×2×cos 120°-12)=-6.故选C .F2 平面向量基本定理及向量坐标运算 13.F2[2018·全国卷Ⅲ] 已知向量a=(1,2),b=(2,-2),c=(1,λ),若c ∥(2a+b ),则λ= . 13.12[解析] 2a+b=(4,2),由c ∥(2a+b )可得14=λ2,即λ=12.20.H8,F2[2018·全国卷Ⅲ] 已知斜率为k 的直线l 与椭圆C :x 24+y 23=1交于A ,B 两点,线段AB 的中点为M (1,m )(m>0). (1)证明:k<-12;(2)设F 为C 的右焦点,P 为C 上一点,且FP ⃗⃗⃗⃗⃗ +FA ⃗⃗⃗⃗⃗ +FB ⃗⃗⃗⃗⃗ =0,证明:2|FP ⃗⃗⃗⃗⃗ |=|FA ⃗⃗⃗⃗⃗ |+|FB ⃗⃗⃗⃗⃗ |. 20.证明:(1)设A (x 1,y 1),B (x 2,y 2),则x 124+y 123=1,x 224+y 223=1.两式相减,并由y 1-y2x 1-x 2=k 得x 1+x 24+y 1+y 23·k=0.由题设知x 1+x 22=1,y 1+y 22=m ,于是k=-34m.由题设得0<m<32,故k<-12. (2)由题意得F (1,0).设P (x 3,y 3),则(x 3-1,y 3)+(x 1-1,y 1)+(x 2-1,y 2)=(0,0).由(1)及题设得x 3=3-(x 1+x 2)=1,y 3=-(y 1+y 2)=-2m<0.又点P 在C 上,所以m=34,从而P (1,-32),|FP ⃗⃗⃗⃗⃗ |=32. 于是|FA ⃗⃗⃗⃗⃗ |=√(x 1-1)2+y 12=√(x 1-1)2+3(1-x 124)=2-x12.同理|FB ⃗⃗⃗⃗⃗ |=2-x22. 所以|FA ⃗⃗⃗⃗⃗ |+|FB ⃗⃗⃗⃗⃗ |=4-12(x 1+x 2)=3. 故2|FP⃗⃗⃗⃗⃗ |=|FA ⃗⃗⃗⃗⃗ |+|FB ⃗⃗⃗⃗⃗ |. 12.F2,F4[2018·江苏卷] 在平面直角坐标系xOy 中,A 为直线l :y=2x 上在第一象限内的点,B (5,0),以AB 为直径的圆C 与直线l 交于另一点D.若AB ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ =0,则点A 的横坐标为 . 12.3 [解析] 因为点A 为直线l :y=2x 上在第一象限内的点,所以可设A (a ,2a )(a>0),则AB 的中点为Ca+52,a ,圆C 的方程为(x-5)(x-a )+y (y-2a )=0.由{(x -5)(x -a)+y(y -2a)=0,y =2x,得D (1,2),则AB ⃗⃗⃗⃗⃗ =(5-a ,-2a ),CD⃗⃗⃗⃗⃗ =-a -32,2-a ,又AB ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ =0,所以(5-a )·-a -32+(-2a )(2-a )=0,解得a=3或a=-1.又a>0,所以a=3,则点A 的横坐标为3.F3 平面向量的数量积及应用4.F3[2018·全国卷Ⅱ] 已知向量a ,b 满足|a|=1,a ·b=-1,则a ·(2a-b )= ( ) A . 4 B . 3C . 2D . 04.B [解析] a ·(2a-b )=2a 2-a ·b=2-(-1)=3,故选B .9.F3[2018·北京卷] 设向量a=(1,0),b=(-1,m ).若a ⊥(ma-b ),则m= .9.-1 [解析] ∵a=(1,0),b=(-1,m ),∴ma-b=(m+1,-m ),又∵a ⊥(ma-b ),∴a ·(ma-b )=m+1=0,即m=-1.8.F1、F3[2018·天津卷]在如图1-2的平面图形中,已知OM=1,ON=2,∠MON=120°,BM ⃗⃗⃗⃗⃗⃗ =2MA ⃗⃗⃗⃗⃗⃗ ,CN ⃗⃗⃗⃗⃗ =2NA ⃗⃗⃗⃗⃗⃗ ,则BC ⃗⃗⃗⃗⃗ ·OM⃗⃗⃗⃗⃗⃗ 的值为 ( )图1-2A . -15B . -9C . -6D . 08.C [解析] 连接MN ,由BM ⃗⃗⃗⃗⃗⃗ =2MA ⃗⃗⃗⃗⃗⃗ ,CN ⃗⃗⃗⃗⃗ =2NA ⃗⃗⃗⃗⃗⃗ ,可得MN ∥BC ,且BC=3MN ,所以BC ⃗⃗⃗⃗⃗ =3MN ⃗⃗⃗⃗⃗⃗⃗ ,所以BC ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ =3MN ⃗⃗⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ =3(ON ⃗⃗⃗⃗⃗⃗ -OM ⃗⃗⃗⃗⃗⃗ )·OM ⃗⃗⃗⃗⃗⃗ =3(ON ⃗⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ -OM ⃗⃗⃗⃗⃗⃗ 2)=3×(1×2×cos 120°-12)=-6.故选C .F4 单元综合 9.F4[2018·浙江卷] 已知a ,b ,e 是平面向量,e 是单位向量.若非零向量a 与e 的夹角为π3,向量b 满足b 2-4e ·b+3=0,则|a-b|的最小值是 ( ) A . √3-1 B . √3+1 C . 2 D . 2-√39.A [解析] 建立平面直角坐标系,设e=(1,0),向量a 与e 的夹角为π3,则向量a 的终点在射线y=√3x (x>0)上.设向量b=(x ,y ),则x 2+y 2-4x+3=0,即(x-2)2+y 2=1,则|a-b|表示圆上任意一点P 到射线y=√3x (x>0)上任意一点A 的距离,显然当A ,P ,C 三点在同一条直线上,即AC 垂直于射线y=√3x (x>0)时,|a-b|取得最小值,最小值为|AC|-1=√3-1,故选A .12.F2,F4[2018·江苏卷] 在平面直角坐标系xOy 中,A 为直线l :y=2x 上在第一象限内的点,B (5,0),以AB 为直径的圆C 与直线l 交于另一点D.若AB ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ =0,则点A 的横坐标为 . 12.3 [解析] 因为点A 为直线l :y=2x 上在第一象限内的点,所以可设A (a ,2a )(a>0),则AB 的中点为Ca+52,a ,圆C 的方程为(x-5)(x-a )+y (y-2a )=0.由{(x -5)(x -a)+y(y -2a)=0,y =2x,得D (1,2),则AB ⃗⃗⃗⃗⃗ =(5-a ,-2a ),CD⃗⃗⃗⃗⃗ =-a -32,2-a ,又AB ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ =0,所以(5-a )·-a -32+(-2a )(2-a )=0,解得a=3或a=-1.又a>0,所以a=3,则点A 的横坐标为3.1.[2018·莱芜期末] 在平行四边形ABCD 中,∠A=60°,AB=2,AD=1,若M ,N 分别是边BC ,CD 上的点(包括端点),且满足|BM⃗⃗⃗⃗⃗⃗⃗ ||BC ⃗⃗⃗⃗⃗⃗ |=|CN⃗⃗⃗⃗⃗⃗ ||CD ⃗⃗⃗⃗⃗⃗ |,则AM ⃗⃗⃗⃗⃗ ·AN ⃗⃗⃗⃗⃗ 的取值范围是 ( )A .[1,3]B .[1,5]C .[2,4]D .[2,5] 1.D[解析] 设|BM⃗⃗⃗⃗⃗⃗⃗⃗ ||BC⃗⃗⃗⃗⃗⃗ |=|CN⃗⃗⃗⃗⃗⃗⃗ ||CD⃗⃗⃗⃗⃗⃗⃗ |=λ,λ∈[0,1],则AM ⃗⃗⃗⃗ ·AN ⃗⃗⃗⃗ =(AB ⃗⃗⃗ +BM ⃗⃗⃗⃗ )·(AD ⃗⃗⃗ +DN ⃗⃗⃗⃗ )=(AB⃗⃗⃗ +λAD ⃗⃗⃗ )·[AD ⃗⃗⃗ +(1-λ)AB ⃗⃗⃗ ]=(1-λ)AB ⃗⃗⃗ 2+λAD⃗⃗⃗ 2+(1+λ-λ2)AB ⃗⃗⃗ ·AD ⃗⃗⃗ =4(1-λ)+λ+12(1+λ-λ2)×2×1=-λ2-2λ+5∈[2,5],故选D .2.[2018·衡阳八中月考] 设向量a=(1,cos θ)与向量b=(-1,2cos θ)垂直,则sin (5π2+2θ)=( )A . √22B . 1C . 0D . -1 2.C[解析] ∵a ⊥b ,∴-1+2cos 2θ=0,即cos 2θ=12,则sin(5π2+2θ)=cos2θ=2cos 2θ-1=2×12-1=0,故选C . 3.[2018·广元期末] 在△ABC 中,AB=2AC=6,BA ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ 2,若点P 是△ABC 所在平面内一点,则当PA ⃗⃗⃗⃗ 2+PB⃗⃗⃗⃗⃗ 2+PC ⃗⃗⃗⃗ 2取得最小值时,AP ⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗ = . 3.-9 [解析] ∵BA⃗⃗⃗ ·BC ⃗⃗⃗ =BA ⃗⃗⃗ 2,∴BA ⃗⃗⃗ ·BC ⃗⃗⃗ -BA ⃗⃗⃗ 2=BA ⃗⃗⃗ ·(BC ⃗⃗⃗ -BA ⃗⃗⃗ )=BA ⃗⃗⃗ ·AC ⃗⃗⃗ =0,∴BA ⃗⃗⃗ ⊥AC ⃗⃗⃗ .以A 为坐标原点,AB ,AC 所在直线分别为x 轴,y 轴建立如图所示的平面直角坐标系,则B (6,0),C (0,3).设P (x ,y ),则PA ⃗⃗⃗ 2+PB ⃗⃗⃗ 2+PC⃗⃗⃗ 2=x 2+y 2+(x-6)2+y 2+x 2+(y-3)2=3x 2-12x+3y 2-6y+45=3[(x-2)2+(y-1)2+10],∴当x=2,y=1时,PA⃗⃗⃗ 2+PB⃗⃗⃗ 2+PC⃗⃗⃗ 2取得最小值,此时AP⃗⃗⃗ ·BC⃗⃗⃗ =(2,1)·(-6,3)=-9.。

一．基础题组 1. 【2011全国1，文3】【答案】B2. 【2008全国1，文5】在ABC △中，AB c =，AC b =．若点D 满足2BD DC =，则AD =（ ） A ．2133b c + B ．5233c b -C ．2133b c - D ．1233b c +【答案】A3. 【2007全国1，文3】已知向量(5,6)a =-，(6,5)b =，则a 与b （ ）A.垂直B.不垂直也不平行C.平行且同向D.平行且反向 【答案】：A【解析】：∵(5)6650a b •=-⨯+⨯=，∴a b ⊥.4. 【2013课标全国Ⅰ，文13】已知两个单位向量a ，b 的夹角为60°，c ＝t a ＋(1－t )b .若b ·c＝0，则t ＝______. 【答案】：2【解析】：∵b ·c ＝0，|a |＝|b |＝1，〈a ，b 〉＝60°，∴a ·b ＝111122⨯⨯=. ∴b ·c ＝[t a ＋(1－t )b ]·b ＝0，即t a ·b ＋(1－t )b 2＝0.∴12t ＋1－t ＝0.∴t ＝2. 5. 【2015高考新课标1，文2】已知点(0,1),(3,2)A B ，向量(4,3)AC =--，则向量BC =( )（A ） (7,4)-- （B ）(7,4) （C ）(1,4)- （D ）(1,4) 【答案】A【解析】∵AB OB OA =-=（3,1），∴BC =AC AB -=(-7,-4)，故选A. 【考点定位】向量运算6.【2016新课标1文数】设向量a =(x ，x +1)，b =(1，2)，且a ⊥b ，则x = . 【答案】23-【考点】向量的数量积及坐标运算【名师点睛】全国卷中向量大多以客观题的形式出现,属于基础题.解决此类问题既要准确记忆公式,又要注意运算的准确性.本题所用到的主要公式是：若()()1122,,,x y x y ==a b ,则1122x y x y ⋅=+a b .二．能力题组1. 【2014全国1，文6】设F E D ,,分别为ABC ∆的三边AB CA BC ,,的中点，则=+FC EBA. B. 21 C. 21D. 【答案】A【解析】根据平面向量基本定理和向量的加减运算可得：在BEF ∆中，12EB EF FB EF AB =+=+，同理12FC FE EC FE AC =+=+，则11111()()()()22222EB FC EF AB FE AC AB AC AB AC AD+=+++=+=+=． 2. 【2009全国卷Ⅰ,文8】设非零向量a 、b 、c 满足|a |=|b |=|c |,a+b =c ,则〈a,b 〉=( )A.150°B.120°C.60°D.30° 【答案】:B 【解析】:如图所示.∵|a |=|b |=|c |,∴△OAB 是正三角形. ∴〈a,b 〉=120°.3. 【2011新课标，文13】已知a 与b 为两个不共线的单位向量,k 为实数,若向量a b +与向量ka b -垂直,则k = . 【答案】1三．拔高题组1. 【2012全国1，文9】△ABC 中，AB 边的高为CD ．若CB ＝a ，CA ＝b ，a ·b ＝0，|a |＝1，|b |＝2，则AD ＝( ) A ．1133-a b B ．2233-a b C ．3355-a b D ．4455-a b 【答案】D【解析】∵a ·b ＝0，∴a ⊥b . 又∵|a |＝1，|b |＝2，∴||5AB=.∴||5CD==.∴2||2AD ==∴4544445()5555AD AB AB===-=-a b a b.2.【2010全国1，文11】已知圆O的半径为1，PA、PB为该圆的两条切线，A、B为两切点，那么PA·PB的最小值为( )A．－4B．－3C．－4＋ D．－3＋【答案】：D3.【2005全国1，文11】点O是三角形ABC所在平面内的一点，满足⋅=⋅=⋅，则点O是ABCOA OB OB OC OC OA∆的（A）三个内角的角平分线的交点（B）三条边的垂直平分线的交点（C）三条中线的交点（D）三条高的交点【答案】B【解析】。

2011—2020年新课标全国卷高考数学试卷分类汇编—平面向量（含全国Ⅰ卷、Ⅱ卷、Ⅲ卷、新高考Ⅰ卷、新高考Ⅱ卷，共 8 套全国卷）一、选择题1、( 20 20 ·全国卷Ⅱ，文 5 ) 已知单位向量 a ， b 的夹角为 60°，则在下列向量中，与 b 垂直的是（）A ． a +2 bB ． 2 a + bC ． a –2 bD ． 2 a – b2、(20 20 ·新高考Ⅰ， 7 ) 已知 P 是边长为 2 的正六边形 ABCDEF 内的一点，则的取值范用是（）A ．B ．C ．D ．3、 (20 20 ·全国卷Ⅲ，理 5 ) 已知向量 a ， b 满足，，，则（）A ．B ．C ．D ．4、(2019·全国卷Ⅰ，理 7 ) 已知非零向量 a ， b 满足，且b ，则 a 与 b 的夹角为（）A ．B ．C ．D ．5、( 2019 ·全国卷Ⅰ，文 8 ) 已知非零向量 a ， b 满足 = 2 ，且（ a - b ） b ，则 a 与 b 的夹角为（）A ．B ．C ．D ．6、 (2019·全国卷Ⅱ，理 3 ) 已知，，，则 = （）A ．B ．C ． 2D ． 37、( 2019 ·全国卷Ⅱ，文3 ) 已知向量，则（）A ．B ． 2C ． 5D ． 508、 (2018·新课标Ⅰ，理 6) 在中，为边上的中线，为的中点，则（）A ．B ．C ．D ．9、(2018·新课标Ⅰ，文 7 ) 在中，为边上的中线，为的中点，则（）A ．B ．C ．D ．10、（ 201 8 ·新课标Ⅱ，理 4 ）已知向量，满足，，，则（）A ． 4B ． 3C ． 2D ． 011、(2018·新课标Ⅱ，文 4 ) 已知向量，满足，，则（）A ． 4B ． 3C ． 2D ． 012、（ 2017 ·新课标Ⅱ， 1 2 理）已知是边长为 2 的等边三角形， P 为平面 ABC 内一点，则的最小值是（）A. B. C. D.13、（ 201 7 ·新课标Ⅱ，文 4 ）设非零向量，满足则（）A ．⊥ B. C. ∥ D.14、（ 2017 ·新课标Ⅲ， 12 ）在矩形中，，，动点在以点为圆心且与相切的圆上．若，则的最大值为（）A ． 3B ．C .D ． 215、（ 2016·新课标Ⅱ， 3 ）已知向量，且，则 m = （）A ． -8B ． -6C ． 6D ． 816、（ 2016·新课标Ⅲ， 3 理，文 3 ）已知向量，，则（）A ．B ．C ．D ．17、（ 201 5 ·新课标Ⅰ， 7 理）设为所在平面内一点，则（）A ．B ．C ．D ．18、(201 5 ·新课标Ⅰ，文 2 ) 已知点 A (0,1) ， B (3,2) ，向量，则向量 ( )A ． (-7,-4)B ． (7,4)C ． (-1,4)D ． (1,4)19、（ 201 5 ·新课标Ⅱ，文 4 ）向量 a = (1 ， - 1) ， b = ( - 1 ， 2) ，则 ( 2a +b ) · a = （）A. - 1B. 0C. 1D. 220、(201 4 ·新课标Ⅰ，文 6 ) 设 D , E , F 分别为Δ ABC 的三边 BC , CA , AB 的中点，则( )A ．B ．C ．D ．21、（ 2014·新课标Ⅱ， 3 理）设向量满足，，则 = （）A ． 1B ． 2C ． 3D ． 522、（ 201 4 ·新课标Ⅱ，文 4 ）设向量满足，，则（）A ． 1B ． 2C ． 3D ． 5。