第三章晶格振动和晶体的热学性质

晶格振动与晶体的热学性质关系综述晶格振动是晶体中原子或分子在平衡位置周围的微小振动。

它是晶体内部热学性质的基础，与晶体的热导率、热膨胀系数、比热容等热学性质密切相关。

本文将综述晶格振动与晶体热学性质的关系，并探讨晶格振动在材料科学中的应用。

晶体的热学性质与晶格振动的频率、波矢以及振幅有密切关系。

一般来说，晶格振动频率高、振幅小的晶体热导率会较高，热膨胀系数较小。

这是因为晶格振动频率高意味着晶格中原子或分子之间的相互作用强，能量传递效率高；而振幅小意味着原子或分子振动的范围小，不易导致晶格的漂移，从而减小了热膨胀系数。

晶格振动与晶体的比热容也存在一定的关系。

在低温下，晶格振动对比热容的贡献为Debye模型所描述的三维声子气模型。

而在高温下，由于激发了大量的非谐振动模式，晶格振动对比热容的贡献将显著增加。

除了热学性质，晶格振动还与晶体的光学性质相关。

例如，晶体的红外吸收谱在一定程度上反映了晶格振动的特点。

由于不同模式的晶格振动对应不同的波矢和能量，因此红外光谱可以提供关于晶体结构和振动特性的重要信息。

在材料科学中，晶格振动也被广泛应用于热电材料和热障涂层等领域。

通过调控晶格振动，可以实现材料的热导率和电导率之间的解耦，从而提高材料的热电性能。

例如，通过引入杂质、界面掺杂或纳米结构等手段，可以有效散射晶格振动，降低热导率，进而提高材料的热电效率。

总之，晶格振动与晶体的热学性质密切相关。

研究晶格振动对于深入理解晶体的热学行为、优化材料的热学性能具有重要意义。

随着计算模拟和实验技术的发展，进一步研究晶格振动与热学性质的关系将有助于推动材料科学和能源领域的进展。

这篇文章主要综述了晶格振动与晶体的热学性质的关系，并探讨了晶格振动在材料科学中的应用。

通过调控晶格振动频率、波矢和振幅等参数，可以实现热导率、热膨胀系数和比热容等热学性质的调控。

此外，晶格振动还与晶体的光学性质相关，并被广泛应用于热电材料和热障涂层等领域。

固体物理第三章班级成绩学号Chapter 3 晶格振动与晶体的热学性质姓名(lattice vibration and its heat characteristics)⼀、简要回答下列问题(answer the following questions):1、在晶格常数为a 的⼀维单原⼦晶格中，波长λ=8a 和波长λ=8a/5的格波所对应的原⼦振动状态有⽆不同? 试画图加以说明。

［答］对于⼀维单原⼦链，由q=2π／λ知，λ＝8a 时，q ＝π／4a ，λ＝8a ／5时，q ＝5π／4a ，⼆者的aq 相差π，不是2π的整数倍，因此，两个格波所对应的原⼦振动状态不同。

如上图，当两个格波的位相差为2π的整数倍时，则它们所对应的原⼦的振动状态相同。

2、什么叫简正振动模式？简正振动数⽬、格波数⽬或格波振动模式数⽬是否是⼀回事？［答］在简谐振动下，由N 个原⼦构成的晶体的晶格振动，可等效成3N 个独⽴的谐振⼦的振动，每⼀个谐振⼦的振动模式称为简正振动模式。

格波振动通常是这3N 个简正振动模式的线性叠加。

简正振动数⽬、格波数⽬或格波振动模式数⽬是是⼀回事，其数⽬等于晶体中所有原⼦的⾃由度之和，即等于3N 。

3、晶体中声⼦数⽬是否守恒？在极低温下，晶体中的声⼦数与温度T 之间有什么样的关系？［答］频率为ωi 的格波的平均声⼦数为： 11)(/-=Tk i B en ωω即每⼀个格波的声⼦数都与温度有关，因此晶体中的声⼦数⽬不守恒，它随温度的改变⽽改变。

以德拜模型为例。

晶体中的声⼦数⽬为ωωωωd g n N D)()('0=其中令 T k x B ω= 则 123'2/033233-=x TB e dxx C T k V N D θπ在极低温度下，θD ／T →∞，于是 331332332033233)2(23123'T nC T Vk e dx x C T k V N n B x B ∑∞=∞=-=ππ即在温度极低时，晶体中的声⼦数⽬与T 3成正⽐。

第三章晶体振动和晶体的热学性质3.1相距为某一常数（不是晶格常数）倍数的两个原子，其最大振幅是否相同？解答：（王矜奉3.1.1，中南大学3.1.1）以同种原子构成的一维双原子分子链为例, 相距为不是晶格常数倍数的两个同种原子, 设一个原子的振幅A, 另一个原子振幅B, 由《固体物理学》第79页公式，可得两原子振幅之比(1)其中m原子的质量. 由《固体物理学》式（3-16）和式（3-17）两式可得声学波和光学波的频率分别为, (2). (3)将(2)(3)两式分别代入(1)式, 得声学波和光学波的振幅之比分别为, (4). (5)由于=，则由(4)(5)两式可得,1B A=. 即对于同种原子构成的一维双原子分子链, 相距为不是晶格常数倍数的两个原子, 不论是声学波还是光学波, 其最大振幅是相同的.3.2 试说明格波和弹性波有何不同？解答：晶格中各个原子间的振动相互关系3.3 为什么要引入玻恩-卡门条件？解答：（王矜奉3.1.2，中南大学3.1.2）（1）方便于求解原子运动方程.由《固体物理学》式（3-4）可知, 除了原子链两端的两个原子外, 其它任一个原子的运动都与相邻的两个原子的运动相关. 即除了原子链两端的两个原子外, 其它原子的运动方程构成了个联立方程组. 但原子链两端的两个原子只有一个相邻原子, 其运动方程仅与一个相邻原子的运动相关, 运动方程与其它原子的运动方程迥然不同. 与其它原子的运动方程不同的这两个方程, 给整个联立方程组的求解带来了很大的困难.（2）与实验结果吻合得较好.对于原子的自由运动, 边界上的原子与其它原子一样, 无时无刻不在运动. 对于有N 个原子构成的的原子链, 硬性假定的边界条件是不符合事实的. 其实不论什么边界条件都与事实不符. 但为了求解近似解, 必须选取一个边界条件. 晶格振动谱的实验测定是对晶格振动理论的最有力验证(《固体物理学》§3.1与§3.6). 玻恩卡门条件是晶格振动理论的前提条件. 实验测得的振动谱与理论相符的事实说明, 玻恩卡门周期性边界条件是目前较好的一个边界条件.3.4 试说明在布里渊区的边界上()/q π=a ，一维单原子晶格的振动解n x 不代表行波而代表驻波。

固体物理第三章晶格振动与晶体热学性质第三章晶格振动与晶体的热学性质晶格振动是描述原子在平衡位置附近的振动，由于晶体内原子间存在着相互作用力，各个原子的振动也不是孤立的，而是相互联系的，因此在晶体内形成各种模式的波。

只有当振动微弱时，原子间非谐的相互作用可以忽略，即在简谐近似下，这些模式才是独立的。

由于晶格的周期性条件，模式所取的能量值不是连续的而是分立的。

对于这些独立而又分立的振动模式，可以用一系列独立的简谐振子来描述。

和光子的情形相似，这些谐振子的能量量子称为声子。

这样晶格振动的总体就可以看成声子系综。

若原子间的非谐相互作用可以看作微扰项，则声子间发生能量交换，并且在相互作用过程中，某些频率的声子产生，某些频率的声子湮灭。

当晶格振动破坏了晶格的周期性，使电子在晶格中的运动受到散射而电阻增加，可以看作电子受到声子的碰撞，晶体中的光学性质也与晶格振动有密切关系，在很大程度上可以看作光子与声子的相互作用乃至强烈耦合。

晶格振动最早是用于研究晶体的热学性质，其对晶体的电学性质、光学性质、超导电性、磁性、结构相变等一系列物理问题都有相当重要的作用，是研究固体宏观性质和微观过程的重要基础。

ωη§3-1 简谐近似和简正坐标由原子受力和原子间距之间的关系可以看出，若离开平衡位置的距离在一定限度，原子受力和该距离成正比。

这时该振动可以看成谐振动.用n μϖ表示原子偏离平衡位置（格点）位移矢量，对于三维空间，描述N 个原子的位移矢量需要3N 个分量，表为)3,,2,1(N i i Λ=μ将体系的势函数在平衡位置附近作泰勒展开:高阶项+∑⎪⎪⎭⎫ ⎝⎛∂∂∂+∑∂∂+===j i N j i j i i N i i V V V V μμμμμμ031,2031021)(第一项为平衡位置的势能，可取为零，第二项为平衡位置的力，等于零。

若忽略高阶项，因为势能仅和位移的平方成正比，即为简谐近似。

23121i N i i m T μ&∑==引入合适的正交变换，将动能和势能用所谓的简正坐标表示成仅含平方∑==N j j ij i i Q a m 31μ项而没有交叉项，即：由分析力学，基本形式的拉格朗日方程为：)32,1(,N i q Q T Q T dt d i i i Λ&==∂∂-⎪⎪⎭⎫ ⎝⎛∂∂其中)32,1(,1N i q f q i j N j j i Λϖϖ=∂∂⋅∑==μ朗日方程：)32,1(,0N i Q L Q L dt d i i Λ&==∂∂-⎪⎪⎭⎫ ⎝⎛∂∂则正则方程为：)3,2,1(,02N i Q Q i i i Λ&&==+ω其解为：)sin(δω+=t A Q i i 当考察某一个j Q 时，则：)sin(δωμ+=t A m a j i iji 晶体参与的振动，且它们的振动频率相同。

黄昆固体物理习题解答第三章晶格振动与晶体的热学性质3.1 已知一维单原子链，其中第j个格波，在第个格点引起的位移为，μ= anj j sin(ωj_j+ σj) ，σj为任意个相位因子，并已知在较高温度下每个格波的平均能量为，具体计算每个原子的平方平均位移。

解：任意一个原子的位移是所有格波引起的位移的叠加，即μn= ∑ μnj=∑ a j sin(ωj t naq j+σj)j j（1）μ2 n =⎛⎜⎝∑μjnj⎞⎛⎟⎜⎠⎝∑μj*nj⎞⎟⎠= ∑μj2nj+ ∑ μ μnj*nj′j j′由于μ μnj⋅nj数目非常大的数量级，而且取正或取负几率相等，因此上式得第2 项与第一项μ相比是一小量，可以忽略不计。

所以2= ∑ μ 2njn j由于μnj是时间的周期性函数，其长时间平均等于一个周期内的时间平均值为μ 2 = 1 T∫0 2 ω+σ 1 2j aj sin( t naqjj j)dt a=j（2）T0 2已知较高温度下的每个格波的能量为KT，μnj的动能时间平均值为1 L T ⎡1 ⎛dμ⎞2 ⎤ρw a2 T 1= ∫ ∫dx0⎢ρnj⎥= j j∫0 2 ω+ σ= ρ 2 2 T⎜⎟dt L a sin( t naq)dt w Lanj T0 0 0 ⎢ 2 ⎝dt⎠⎥2T0 j j j j 4 j j其中L 是原子链的长度，ρ 使质量密度，T0为周期。

1221所以Tnj= ρ w La j j=KT（3）4 2μKT因此将此式代入（2）式有nj2 = ρ ωL 2 jμ所以每个原子的平均位移为2== ∑ μ 2= ∑KT= KT∑1n njρ ωL2ρLω2j j j j j3.2 讨论 N 个原胞的一维双原子链（相邻原子间距为 a），其 2N 格波解，当 M=m 时与一维单原子链的结果一一对应.解答（初稿）作者季正华- 1 -黄昆固体物理习题解答解：如上图所示，质量为M 的原子位于2n-1，2n+1，2n+3 ……质量为m 的原子位于2n，2n+2，2n+4 ……牛顿运动方程：..mμ2n= −β μ(22n−μ2n+1 −μ2n−1)..Mμ2n+1 = −β μ(22n+1 −μ2n+2 −μ2n)体系为N 个原胞，则有2N 个独立的方程i na q方程解的形式：iμ2n=Ae[ωt−(2 ) ] μ2n+1=Be[ω−(2n+1)aq]na qμ=将μ2n=Ae[ωt−(2 ) ]2n+1 Be i[ωt−(2n+1) aq]代回到运动方程得到若A、B 有非零的解，系数行列式满足：两种不同的格波的色散关系：——第一布里渊区解答（初稿）作者季正华- 2 -第一布里渊区允许 q 的数目黄昆 固体物理 习题解答对应一个 q 有两支格波：一支声学波和一支光学波。

第三章 晶格振动与晶体的热学性质1。

什么是简谐近似？解:当原子在平衡位置附近作微小振动时，原子间的相互作用可以视为与位移成正比的虎克力，由此得出原子在其平衡位置附近做简谐振动。

这个近似即称为简谐近似。

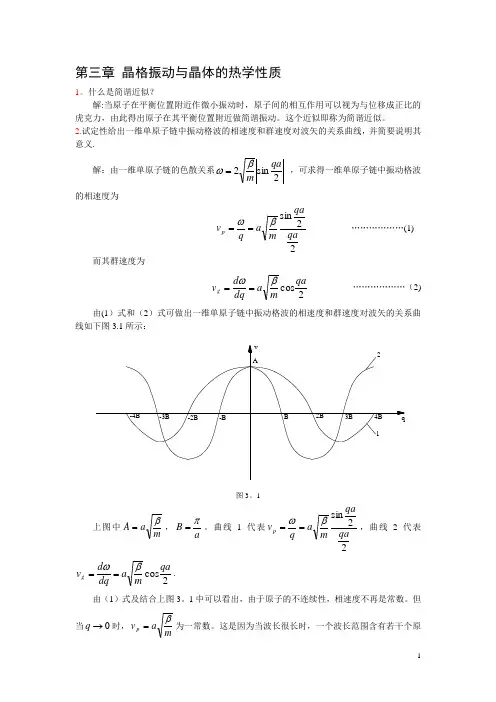
2.试定性给出一维单原子链中振动格波的相速度和群速度对波矢的关系曲线，并简要说明其意义.解：由一维单原子链的色散关系2sin2qamβω= ，可求得一维单原子链中振动格波的相速度为22sinqa qamaqv p βω== (1)2cos qam a dq d v g βω==. 由（1）式及结合上图3。

1中可以看出，由于原子的不连续性，相速度不再是常数。

但当0→q 时，mav p β=为一常数。

这是因为当波长很长时，一个波长范围含有若干个原子，相邻原子的位相差很小，原子的不连续效应很小，格波接近与连续媒质中的弹性波。

由（2）式及结合上图3。

1中可以看出，格波的群速度也不等于相速度.但当0→q ，mav v p g β==，体现出弹性波的特征，当q 处于第一布区边界上，即aq π=时，0=g v ,而mav p βπ2=，这表明波矢位于第一布里渊区边界上的格波不能在晶体中传播，实际上它是一种驻波。

3。

周期性边界条件的物理含义是什么？引入这个条件后导致什么结果?如果晶体是无限大,q 的取值将会怎样？解：由于实际晶体的大小总是有限的,总存在边界，而显然边界上原子所处的环境与体内原子的不同，从而造成边界处原子的振动状态应该和内部原子有所差别。

考虑到边界对内部原子振动状态的影响,波恩和卡门引入了周期性边界条件.其具体含义是设想在一长为Na 的有限晶体边界之外，仍然有无穷多个相同的晶体，并且各块晶体内相对应的原子的运动情况一样，即第j 个原子和第j tN +个原子的运动情况一样，其中t ＝1,2，3…。

引入这个条件后，导致描写晶格振动状态的波矢q 只能取一些分立的不同值。

如果晶体是无限大,波矢q 的取值将趋于连续。

第三章晶体振动和晶体的热学性质（12学时）晶体内的原子并非在各自的平衡位置上固定不动，而是围绕其平衡位置作振动，并且由于原子之间存在着相互作用力，因而各个原子的振动是相互联系着的，这样在晶体中就形成了各种模式的机械波。

晶格振动对固体的比热、热膨胀、热导等性质有重要的影响。

本章将向大家介绍晶格振动的一般性质。

基本要求：掌握一维晶体振动模式的色散关系，晶格振动的量子化、声子的概念。

爱因斯坦模型和德拜模型解释固体的比热性质。

了解非谐效应，确定振动谱的实验方法以及晶格的自由能。

基本内容：1、一维原子链的振动，色散关系、格波2、晶格振动的量子化、声子，长波近似3、固体比热，爱因斯坦模型和德拜模型4、非简谐效应5、确定振动谱的实验方法，晶格的自由能重点：一维晶体振动模式的色散关系，晶格振动的量子化、声子的概念，爱因斯坦模型和德拜模型。

难点：晶格振动的量子化、声子的概念。

§3.1 一维原子链的振动晶格振动最简单的情形就是一维晶格的振动，本节将介绍一维原子链的振动情况及其色散关系。

通过简单情形的讨论，把所得的一些主要结论和主要方法加以推广，应用到复杂的三维晶格的振动。

一、一维简单格子的情形1、一维简单格子的振动晶体内的原子围绕其平衡位置在不停地振动，由于原子间存在着相互作用力，各个原子之间的振动相互关联，从而在晶体中形成了各种模式的机械波。

（1）、简谐近似和最近邻近似一维简单格子是最简单的情形，考虑一个一维原子链，每个原子具有相同的质量m，平衡时原子间距为a。

由于热运动各原子离开了平衡位置，用x n代表第n个原子离开平衡位置的位移，第n个和第n+1个原子间的相对位移就为x n+1-x n，和第n-1个原子间的相对位移就为x n-x n-1。

只考虑最近邻原子间的简谐相互作用，其恢复力常数为 。

（2）、运动方程对第n 个原子进行受力分析，列牛顿定律方程可得运动方程为:)()(1122-+---=n n n n nx x x x dtx d m ββ )2(1122n n n nx x x dtx d m -+=-+β（n=1、2、…、N ） 式中β为原子间简谐相互作用的恢复力常数。