连续时间信号傅里叶变换及调制定理

αt
1
单边指数函数e-αt; (b) e-αt
的幅度谱
o
(b)
F(j) f(t)ejtdt etejtdt
01 02 e(j)t (j)
01j
1
ja rcta n
ea
a22
其振幅频谱及相位频谱分
解
别为
F ( ) 1
2 2
( ) arctan
例 2.4-3 求图 2.43(a)所示 双边指数 函数的频 谱函数。
02 或
2
B
2(rad/s)
1
Bf
(Hz)
周期信号的能量是无限的，而其平均功率是有界的， 因而周期信号是功率信号。为了方便，往往将周期信 号在1Ω电阻上消耗的平均功率定义为周期信号的功率。 显然，对于周期信号f(t)， 无论它是电压信号还是电
流信号，其平均功率均为 T
12 2
P f (t)dt 2.3.3 周期信号的功率T T2
( )
02
－
4
－
2
o
门函数； (b) 门函数的频谱；－ 4(c)－幅2 度谱； (d) 相位谱
o 2 4
2 4
－
(c)
(d )
f
(t)
e at
0
f (t)
例 2.4-2 求指数函数f(t)
的1频 谱 函 数 。 e－t (＞0)
o
t
(a)
t 0 ( 0)
t 0
图 2.4-2 单边指F(数)函数e-
性。
2.2 周期信号的连续时间傅里叶级数
f (t) Fnejnt
2.2.1 指数形式的傅里叶级数 n
满足Dirichlet条件的周期函数可以展成复指数形式的傅里叶级数:

√ √ √ √
时域周期冲激序列 δ T1 (t ) =
t − ( )2
n =−∞
∑ δ (t − nT1 ) ↔ ω1 ∑ δ (ω − nω1 ) = δω (ω ) 频域周期冲激序列
n =−∞
1
+∞
+∞
√
钟形脉冲 e
τ
钟形脉冲 πτ e
τ ⎡
2⎢ ⎣ Sa
−(
ωτ
2
)2
矩形调幅 cos ω0t ⎡u(t +τ ) −u(t −τ )⎤ ⎢ ⎥
√ √ √ √
F (t ) ↔ 2πf (−ω ) f (t )e jω0 t (− jt ) f (t ) πf (0)δ (t ) + f (t ) p(t ) f (t ) − jt F (ω − ω 0 ) F '(ω )
f (t − t 0 ) f '(t )
F (ω )e− jωt0 jω F (ω ) πF (0)δ (ω ) + F (ω ) jω
jω0 t
√ √ √ √ √
⎧ 1, t > 0 ⎪ 符号 sgn(t ) = ⎨ 0, t = 0 ⎪−1, t < 0 ⎩
冲激延时 δ (t − t 0 ) 余弦 cos(ω0 t ) 正弦 sin(ω0 t )
⎧− j, ω > 0 ⎪ F (ω ) = ⎨ 0, ω = 0 ⎪ ⎩ j, ω < 0
(n + 1)a n u (n) (n + 1)! a n u ( n) (n + k − 1)!k !
z , z > a z−a
z , z > a ( z − a) 2 z2 , z > a ( z − a) 2 z k +1 , z > a ( z − a ) k +1

（3）周期信号的傅里叶变换；
（4）频域分析法分析系统；
（5）系统的无失真传输；
（6）理想低通滤波器；
（7）系统的物理可实现性；
3.3本章的内容摘要
3.3.1信号的正交分解
两个矢量 和 正交的条件是这两个矢量的点乘为零，即：
如果 和 为相互正交的单位矢量，则 和 就构成了一个二维矢量集，而且是二维空间的完备正交矢量集。也就是说，再也找不到另一个矢量 能满足 。在二维矢量空间中的任一矢量 可以精确地用两个正交矢量 和 的线性组合来表示，有
条件1：在一周期内，如果有间断点存在，则间断点的数目应是有限个。
条件2：在一周期内，极大值和极小值的数目应是有限个。
条件3:在一周期内，信号绝对可积，即
（5）周期信号频谱的特点
第一：离散性，此频谱由不连续的谱线组成，每一条谱线代表一个正弦分量，所以此谱称为不连续谱或离散谱。
第二：谐波性，此频谱的每一条谱线只能出现在基波频率 的整数倍频率上。
(a)周期、连续频谱； (b)周期、离散频谱；
(c)连续、非周期频谱； (d)离散、非周期频谱。
答案：(d)
题7、 的傅里叶变换为
答案：
分析：该题为典型信号的调制形式
题8、 的傅里叶变换为
答案：
分析：根据时移和频移性质即可获得
题9、已知信号 如图所示，且其傅里叶变换为
试确定：
(1)
(2)
(3)
解：
(1)将 向左平移一个单位得到
对于奇谐函数，满足 ，当 为偶数时， ， ；当 为奇数时， ， ，即半波像对称函数的傅里叶级数展开式中只含奇次谐波而不含偶次谐波项。
（4）周期信号傅里叶级数的近似与傅里叶级数的收敛性
一般来说，任意周期函数表示为傅里叶级数时需要无限多项才能完全逼近原函数。但在实际应用中，经常采用有限项级数来代替无限项级数。无穷项与有限项误差平方的平均值定义为均方误差，即 。式中， ， 。研究表明， 越大， 越小，当 时， 。

F( j)
πF (0)
()
若信号不存在直流分量即F(0)=0
则t
f
( )d
F
1
j
F( j)
18
例3 试利用积分特性求图示信号f(t)的频谱函数。
f(t) 1
y(t)=p(t0.5) 1
t
0
1
t
0
1
解： f (t) = t p(t 0.5)dt = t y(t)dt
由于 p(t 0.5) F Y ( j) = Sa (0.5)e j0.5
F F1 ( j)
1 Sa (0.5)e j0.5 j
利用修正的微分特性，可得
F( j) = π( f () f ()) () F1 ( j) j
= 3π () 1 Sa (0.5)ej0.5 j
与例4结果 一致！ 24
23
10. 频域微分积分特性
若f (t) F( j)
则( jt)n f (t) F (n) ( j)
由上式利用时域微分特性，得
2
F[ f '(t)] = (j)F(j) = A 2jsin( )
2
因此有
F( j) = 2A sin( ) = ASa( )
2
2
21
20
例6 试利用微分特性求图示信号f(t)的频谱函数。
f(t) 2 1
f '(t) 1
t
0
1
t
0
1
解： f '(t) = p(t 0.5) F Sa(0.5)e j0.5
f1(t) d n f (t
f )
2 (t) F F ( j)
1
2π n
[F1( j) F( j)

（1） 在调用函数fourier( )及ifourier( )之前， 要用syms命令对所有需要用到的变量 （如t,u,v,w） 等进行说明，即要将这些变量说明成符号变量。对fourier( )中的f及ifourier( )中的F也要用符 号定义符sym将其说明为符号表达式。 （2） 采用fourier( )及fourier( )得到的返回函数， 仍然为符号表达式。 在对其作图时要用ezplot( ) 函数，而不能用plot()函数。 （3）fourier( )及fourier( )函数的应用有很多局限性，如果在返回函数中含有δ(ω)等函数，则 ezplot( )函数也无法作出图来。另外，在用fourier( )函数对某些信号进行变换时，其返回函数 如果包含一些不能直接表达的式子，则此时当然也就无法作图了。这是fourier( )函数的一个 局限。另一个局限是在很多场合，尽管原时间信号f(t)是连续的，但却不能表示成符号表达 式，此时只能应用下面介绍的数值计算法来进行傅氏变换了，当然，大多数情况下，用数值 计算法所求的频谱函数只是一种近似值。 例 求门函数 f (t ) = ε (t + 1) − ε (t − 1) 的傅里叶变换，并画出幅度频谱图
调制器 调制波 已调波
所示
f (t )
载 波
y ( t ) = f ( t ) cos ω 0 t
cos ω 0 t
从频域上看，已调制信号y(t )的频谱为原调制信号f (t)的频谱搬移到 ±w0 处，幅 度降为原F( jw)的 1/2，即
1 f (t ) cos ω0t ↔ [ F (ω + ω0 ) + F (ω − ω0 )] 2
（2）、傅里叶变换的数值计算实现法 严格说来，如果不使用 symbolic 工具箱，是不能分析连续时间信号的。采用数值计算 方法实现连续时间信号的傅里叶变换，实质上只是借助于 MATLAB 的强大数值计算功能， 特别是其强大的矩阵运算能力而进行的一种近似计算。 傅里叶变换的数值计算实现法的原理 如下： 对于连续时间信号 f(t)，其傅里叶变换为：

• 直到19世纪末，制造出电容器。20世纪初，谐振电路、滤波
器、正弦振荡器等一系列问题的解决为正弦函数与傅里叶分 析的在通信系统中的应用开辟了广阔的前景。 • 从此，在通信与控制系统的理论研究和实际应用之中，采用 频率域（频域）的分析方法比经典的时间域（时域）方法有 许多突出的优点。 • 当今，傅里叶分析方法已成为信号分析与系统设计不可缺少 的重要工具。 • 20世纪70年代，出现的各种二值正交函数（沃尔什函数）， 它对通信、数字信号处理等技术领域的研究提供了多种途径 和手段。使人们认识到傅里叶分析不是信息科学与技术领域 中唯一的变换域方法。
nw1 nw1

0
w
nw1
w1 0 w1
nw1
w
正、负频率相应项成对合并，才是实际频谱函数。
4.周期信号的功率特性
—时域和频域能量守恒定理
周期信号的平均功率P：在一个周期内求平方再求积分。
1 t0 T1 2 f (t )dt P f (t ) t T1 0 1 1 2 2 2 2 2 a0 ( an bn ) c0 cn 2 n 1 2 n 1
其傅里叶级数三角展开式中 仅含基波和奇次谐波
例子
例如：奇谐函数
f (t )
E 2
T1 2
f (t )
E 2
T 1 2
0
E 2
T1 2
t
0
E 2
T1 2
t
sin( w1t )
E 2
f (t )
E 2
T1 2 T 1 2 T1 2
f (t )
0
E 2
t

0
E 2
T1 2

0 21
/4
/2
(b)相位图
图2.1-2例2.1-2的频谱图
二、指数形式的傅里叶级数
利用欧拉公式将三角形式的傅里叶级数，表示为 复指数形式的傅氏级数
其中
f t F n1 e jn1t
n
F n1
1 T
t0 T t0
f t e jn1tdt
F n1 是复常数，通常简写为 Fn 。
21t
5
4
2
sin
1t
1 2
sin
31t
解：将 f t 整理为标准形式
f
(t)
1
2cos 1t来自4cos 21t
5
4
1 2
cos
31t
2
1
2
cos
1t
4
cos
21t
4
1 2
cos
31t
2
振幅谱与相位谱如图2-1所示。
cn
2
1
1
1/2
0 1 21 31
(a) 振幅图
n
/4
31
第二章 连续时间信号与系统的频域分析 ——Fourier变换
2. 1 周期信号的傅里叶级数分析 2. 2 非周期信号的频谱--傅里叶变换 2. 3 傅里叶变换的性质及定理 2. 4 系统的频域分析方法 2. 5 无失真传输系统与滤波
LTI系统分析的一个基本任务，是求解系统对任意 激励信号的响应，基本方法是将信号分解为多个基本信 号元。
一、三角形式傅里叶级数
周期信号: f t f t nT
其中
T
是信号的最小重复时间间隔，f1
1 是信号的基波频率。 T
若 f t 满足狄里赫利条件，则 f t 可以展开为三角形

FT x(t ) ←⎯→ X ( jΩ )
FT x ( t ) e jΩ 0 t ← ⎯→ X [ j ( Ω − Ω 0 )]
ℱ x ( t ) e jΩ 0 t
{
} = ∫ x (t ) e
−∞
∞
∞
jΩ 0 t
e − j Ω t dt =
−∞
∫
x ( t ) e − j ( Ω − Ω 0 ) t dt
19
设
X ( jΩ) = X ( jΩ) e jϕ( Ω ) = X R (Ω) + jX I (Ω)
X * ( jΩ) = X ( jΩ) e − jϕ( Ω ) = X R (Ω) − jX I (Ω)
于是
X * (− jΩ) = X (− jΩ) e − jϕ( − Ω ) = X R (−Ω) − jX I (−Ω)
jtx ( t ) e
− jΩ t
dt
dX ( j Ω ) tx ( t ) ← ⎯→ j dΩ
FT
例如： du ( t )
dt
= δ (t )
对应的傅里叶变换
jΩ 1 = j 0 ⋅ πδ ( Ω ) + =1 δ(t ) ←⎯→ jΩ[πδ(Ω) + ] jΩ jΩ
FT
再例如：
1 d [πδ ( Ω ) + ] 1 jΩ FT ′ = jπ δ ( Ω ) − 2 tu ( t ) ← ⎯→ j Ω dΩ
x(t )
1
τ −2 τ 2
τ
X ( jΩ )
t
2π τ
Ω
τ
X ( jt )
x (Ω )
2π
若x(t)是偶对称的，则
FT X ( jt ) ←⎯→ 2πx(Ω)

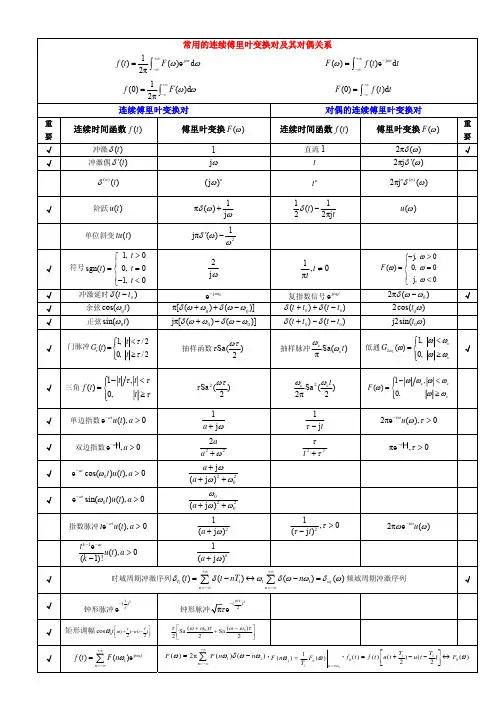
傅里叶变换调制定理公式傅里叶变换调制定理公式是一个重要的信号处理公式，在通信系统中起着关键作用。

它是傅里叶变换和调制原理的结合，能够帮助我们理解信号在频域中的特性以及信号的传输和解调过程。

本文将详细解释傅里叶变换调制定理公式的含义、应用和相关概念。

傅里叶变换调制定理公式是指在信号的频域中，调制操作等效于在时域中信号与载波进行频谱平移的操作。

它的数学表达式为：s(t) = Re{F^(-1)[S(f) · e^(j2πf_ct)]}其中，s(t)表示调制后的信号，在时域中表示；F^(-1)表示傅里叶逆变换；S(f)表示信号在频域中的频谱；e^(j2πf_ct)表示频率为f_c的载波；Re表示取复数的实部。

这个公式表明，调制信号可以通过将信号的频谱与载波频谱进行乘积，并根据需要对结果进行频谱平移得到。

傅里叶变换调制定理公式是基于调制原理和傅里叶变换的基本性质推导而来的。

通过将信号与载波相乘，可以将信号的频谱平移到载波频率附近，并实现在频域中的调制操作。

这个操作在通信系统中非常重要，比如调幅调制（AM）、调频调制（FM）和调相调制（PM）等。

在通信系统中，调制操作是将基带信号转换为适合传输的高频信号的过程。

傅里叶变换调制定理公式可以帮助我们理解调制的原理和特性。

通过对信号在频域中的变换和平移操作，我们可以获得调制后的信号，从而实现信号的传输、解调和恢复。

除了理解调制的原理和特性，傅里叶变换调制定理公式还可以应用于信号分析和系统设计等领域。

在信号分析中，我们可以利用该公式对信号的频谱进行研究，了解信号的频域特性。

在系统设计中，我们可以利用该公式进行信号处理和频谱设计，从而优化系统性能。

此外，傅里叶变换调制定理公式还与其他傅里叶变换性质和定理有着密切的关系。

例如，与时域和频域的对称性相关的奇偶性定理、线性性质和卷积定理等，都与傅里叶变换调制定理有着相互联系。

这些定理和性质共同构成了傅里叶变换理论的重要组成部分，在信号处理领域具有广泛的应用。

连续信号的傅里叶变换一、引言连续信号的傅里叶变换是信号处理领域中非常重要的一部分。

它可以将时域上的连续信号转换为频域上的频谱，从而方便我们对信号进行分析和处理。

在本文中，我们将详细介绍连续信号的傅里叶变换的相关概念、公式以及应用。

二、连续信号与傅里叶变换1. 连续信号在信号处理领域中，连续信号是指在时间上是连续的函数。

它可以表示为：f(t) = A*cos(ωt + φ)其中，A表示振幅，ω表示角频率，φ表示相位。

2. 傅里叶变换傅里叶变换是一种将时域上的函数转换为频域上函数的方法。

对于一个连续信号f(t)，它的傅里叶变换F(ω)可以表示为：F(ω) = ∫f(t)*exp(-jωt)dt其中，j为虚数单位。

3. 傅里叶变换公式对于一个实数函数f(t)，其傅里叶变换F(ω)和反变换f(t)可以表示为：F(ω) = ∫f(t)*exp(-jωt)dtf(t) = (1/2π)∫F(ω)*exp(jωt)dω4. 傅里叶变换的性质傅里叶变换具有许多重要的性质，包括线性性、平移性、卷积定理等。

这些性质使得傅里叶变换在信号处理中得到了广泛的应用。

三、连续信号的频域表示1. 频谱对于一个连续信号f(t)，它的频谱是指在频域上表示该信号的振幅和相位信息。

通常情况下，我们将频谱表示为F(ω)或S(ω)，其中F(ω)为傅里叶变换结果，S(ω)为傅里叶变换结果的幅度谱。

2. 幅度谱和相位谱对于一个连续信号f(t)，它的频谱可以分解为振幅和相位两个部分。

振幅谱指的是在不同频率下该信号振动的强度大小，而相位谱则表示不同频率下该信号振动相对于某个参考点所处的相位差。

四、应用举例1. 语音信号处理语音信号是一种典型的连续信号，在语音处理领域中，傅里叶变换被广泛应用于声学特征提取、语音识别等方面。

通过对语音信号的傅里叶变换，我们可以得到该信号在不同频率下的频谱信息，从而方便我们进行特征提取和分类。

2. 图像处理图像信号也是一种连续信号，在图像处理领域中，傅里叶变换被广泛应用于图像滤波、图像增强等方面。

调制过程
在调制过程中，原始信号的频谱被搬移到载波的频率上，形成调制信号的频谱。 调制方式的不同会导致频谱形状和带宽的变化。
解调过程
在解调过程中，调制信号的频谱被还原为原始信号的频谱。解调方式的不同会 影响还原的准确性和信噪比。
滤波器设计与应用
滤波器类型
滤波器应用
根据滤波器的频率响应特性，可分为 低通、高通、带通和带阻滤波器等类 型。
滤波器在通信系统中具有广泛的应用， 如去除噪声、分离信号、实现特定频 带内的信号传输等。
滤波器设计
滤波器设计需要考虑滤波器的类型、 截止频率、通带波纹、阻带衰减等参 数，可采用窗函数法、频率采样法等 方法进行设计。
PART 03
离散时间信号傅立叶变换
离散时间信号频谱分析
频谱概念
频谱是频率域中对信号进行描述 的一种方式，表示信号在不同频
数字滤波器设计与应用
数字滤波器类型
包括低通、高通、带通和带阻滤波器等，不同类型的滤波器具有不 同的频谱特性。
数字滤波器设计方法
基于窗函数法、频率采样法和优化算法等进行设计，实现所需的滤 波功能。
数字滤波器应用
在通信系统中用于滤除噪声和干扰，提高信号质量；在图像处理中用 于平滑图像和锐化边缘等；在音频处理中用于实现音效和降噪等。
实验目的和要求
01
02
03
04
掌握傅立叶变换的基本原理和 性质；
熟悉傅立叶变换在通信原理中 的应用；
学会使用相关设备和软件进行 傅立叶变换实验；
分析实验结果，加深对傅立叶 变换的理解。
实验环境和设备配置
01
02
03
04
计算机
配置有MATLAB或Python等 数学计算软件；

信号与系统常用公式信号与系统是现代电子信息工程学科中的重要基础课程，它涉及到了信号的产生、传输和处理等方面的知识。

在学习和应用信号与系统的过程中，我们经常会使用到一些公式和定理。

本文将为大家介绍一些信号与系统中常用的公式和定理，希望能对大家的学习和工作有所帮助。

一、信号的基本性质：1.基本信号及其性质：矩形信号：rect(t/T) =1，-T/2≤t≤T/20，其他三角信号：tri(t/T) =1-，t/T，-T≤t≤T0，其他正弦信号：sin(ωt) = （e^jωt - e^(-jωt))/(2j)余弦信号：cos(ωt) = （e^jωt + e^(-jωt))/22.对称性：奇对称信号：如果s(t)=-s(-t)，则s(t)是奇对称信号。

偶对称信号：如果s(t)=s(-t)，则s(t)是偶对称信号。

3.平均功率：平均功率：P = lim(T→∞)1/T ∫_(T/2)^(T/2) ，s(t)，^2 dt4.交流分量：交流分量：s_AC=1/2*[s(t)-s_DC]二、线性时不变系统的基本性质：1.线性时不变系统的定义：线性性：s_1(t)+s_2(t)—>LTI—>s_1(t)+s_2(t)时不变性：s(t-t_0)—>LTI—>s(t-t_0)2.系统的冲激响应：系统的冲激响应：h(t) = d(s(t))/dt，其中d是微分算子。

3.系统的单位阶跃响应：系统的单位阶跃响应：H(t)=∫_(-∞)^th(τ)dτ4.线性卷积定理：线性卷积定理：s_1(t)*s_2(t)—>LTI—>S_1(ω)*S_2(ω)三、频域分析：1.傅里叶级数：傅里叶级数：s(t)=∑_(n=-∞)^∞C_n*e^(jω_nt)，其中C_n是频谱系数，ω_n是频率。

2.傅里叶变换：傅里叶变换：S(ω) = ∫_(-∞)^∞ s(t) * e^(-jωt) dt3.周期信号的频谱：周期性信号的频谱：S(ω)=∑_(k=-∞)^∞(1/T)*S(kω_0)*δ(ω-kω_0)，其中S(kω_0)是周期频谱系数。

傅立叶变换的原理、意义和应用1概念：编辑傅里叶变换是一种分析信号的方法，它可分析信号的成分，也可用这些成分合成信号。

许多波形可作为信号的成分，比如正弦波、方波、锯齿波等,傅里叶变换用正弦波作为信号的成分.参考《数字信号处理》杨毅明著p.89，机械工业出版社2012年发行。

定义f(t）是t的周期函数，如果t满足狄里赫莱条件:在一个周期内具有有限个间断点，且在这些间断点上，函数是有限值；在一个周期内具有有限个极值点;绝对可积。

则有下图①式成立。

称为积分运算f(t）的傅里叶变换,②式的积分运算叫做F（ω)的傅里叶逆变换。

F（ω）叫做f(t）的像函数，f(t）叫做F(ω）的像原函数。

F(ω)是f（t）的像。

f（t）是F（ω)原像。

①傅里叶变换②傅里叶逆变换中文译名Fourier transform或Transformée de Fourier有多个中文译名，常见的有“傅里叶变换”、“付立叶变换"、“傅立叶转换”、“傅氏转换”、“傅氏变换"、等等。

为方便起见，本文统一写作“傅里叶变换”。

应用傅里叶变换在物理学、电子类学科、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用（例如在信号处理中，傅里叶变换的典型用途是将信号分解成幅值谱——显示与频率对应的幅值大小）。

相关* 傅里叶变换属于谐波分析.* 傅里叶变换的逆变换容易求出，而且形式与正变换非常类似；＊正弦基函数是微分运算的本征函数，从而使得线性微分方程的求解可以转化为常系数的代数方程的求解.在线性时不变的物理系统内，频率是个不变的性质,从而系统对于复杂激励的响应可以通过组合其对不同频率正弦信号的响应来获取;*卷积定理指出：傅里叶变换可以化复杂的卷积运算为简单的乘积运算,从而提供了计算卷积的一种简单手段;* 离散形式的傅立叶变换可以利用数字计算机快速地算出（其算法称为快速傅里叶变换算法（FFT))。

由时不变性： δ(t -τ)
h(t -τ)
由齐次性： f (τ)δ(t -τ)
f (τ) h(t -τ)
由叠加性：

f
()(t
)
d


f
()h(t
)d
‖
‖
f (t)
yf(t)
yf (t)
f()h(t)d卷积积分，要理解

第2-16页
■
连续时间信号与系统的频域分析
信号与系统 电子教案
4.4 傅里叶变换
非周期信号的频谱—傅里叶变换
一、傅里叶变换
非周期信号f(t)可看成是周期T→∞时的周期信号。 前已指出当周期T趋近于无穷大时，谱线间隔趋 近于无穷小，从而信号的频谱变为连续频谱。各频率 分量的幅度也趋近于无穷小，不过，这些无穷小量之 间仍有差别。 为了描述非周期信号的频谱特性，引入频谱密度的 概念。令
第4-33页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 • 幅度调制的例子
第4-34页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.5 傅里叶变换的性质
四.能量定理（帕斯瓦尔关系）
(Parseval’s Relation for Aperiodic Signals)
F(j)T l i m 1F /T n T l i m FnT (单位频率上的频谱）
称F(jω)为频谱密度函数。
第4-22页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
• 对密度的理解例子 • 设粉笔的质量为M，均匀地分布在体积V上，将体
积V分成许多体积为ΔV的小单元，每个小单元质 量为ΔM，当ΔV→0时，ΔM→0.于是定义密度

傅里叶变换的基本性质（一）傅里叶变换建立了时间函数和频谱函数之间转换关系。

在实际信号分析中，经常需要对信号的时域和频域之间的对应关系及转换规律有一个清楚而深入的理解。

因此有必要讨论傅里叶变换的基本性质，并说明其应用。

一、线性傅里叶变换是一种线性运算。

若则其中a和b均为常数，它的证明只需根据傅里叶变换的定义即可得出。

例3-6利用傅里叶变换的线性性质求单位阶跃信号的频谱函数。

解因由式(3-55)得二、对称性若则证明因为有将上式中变量换为x，积分结果不变，即再将t用代之，上述关系依然成立，即最后再将x用t代替，则得所以证毕若是一个偶函数，即，相应有，则式(3-56)成为可见，傅里叶变换之间存在着对称关系，即信号波形与信号频谱函数的波形有着互相置换的关系，其幅度之比为常数。

式中的表示频谱函数坐标轴必须正负对调。

例如：例3-7若信号的傅里叶变换为试求。

解将中的换成t，并考虑为的实函数，有该信号的傅里叶变换由式(3-54)可知为根据对称性故再将中的换成t，则得为抽样函数，其波形和频谱如图3-20所示。

三、折叠性若则四、尺度变换性若则证明因a＞0，由令，则，代入前式，可得函数表示沿时间轴压缩(或时间尺度扩展)a倍，而则表示沿频率轴扩展(或频率尺度压缩)a倍。

该性质反映了信号的持续时间与其占有频带成反比，信号持续时间压缩的倍数恰好等于占有频带的展宽倍数，反之亦然。

例3-8已知,求频谱函数。

解前面已讨论了的频谱函数，且根据尺度变换性，信号比的时间尺度扩展一倍，即波形压缩了一半，因此其频谱函数两种信号的波形及频谱函数如图3-21所示。

五、时移性若则此性质可根据傅里叶变换定义不难得到证明。

它表明若在时域平移时间，则其频谱函数的振幅并不改变，但其相位却将改变。

例3-9求的频谱函数。

解:根据前面所讨论的矩形脉冲信号和傅里叶变换的时移性，有六、频移性若则证明证毕频移性说明若信号乘以，相当于信号所分解的每一指数分量都乘以，这就使频谱中的每条谱线都必须平移，亦即整个频谱相应地搬移了位置。

信号与系统常用公式汇总_1.傅里叶级数公式：信号x(t)的周期为T时，它的傅里叶级数展开式为：x(t) = a0 + Σ(an*cos(nω0t) + bn*sin(nω0t))，其中n为整数，ω0 = 2π/T，an和bn为傅里叶系数。

2.傅里叶变换公式：连续时间信号x(t)的傅里叶变换为：X(ω) = ∫( -∞到+∞ ) x(t)*e^(-jωt)dt。

3.逆傅里叶变换公式：连续频率信号X(ω)的逆傅里叶变换为：x(t)=(1/2π)*∫(-∞到+∞)X(ω)*e^(jωt)dω。

4.傅里叶变换对称性：X(-ω)=X(ω)*，即傅里叶变换对称于原点。

5.卷积定理：连续时间卷积的傅里叶变换等于信号的傅里叶变换之积，即：x(t)*h(t)的傅里叶变换为X(ω)*H(ω)。

6.系统频率响应：系统的频率响应H(ω)是指系统对频率为ω的输入信号的增益和相位的影响。

7.系统单位冲激响应：系统对单位冲激信号δ(t)的响应称为系统的单位冲激响应h(t)。

8.系统的冲激响应和频率响应的关系：系统的冲激响应h(t)和频率响应H(ω)满足傅里叶变换的关系：H(ω) = ∫( -∞到+∞ ) h(t)*e^(-jωt)dt。

9.系统的传递函数：系统的传递函数H(ω)是频率响应H(ω)的傅里叶变换。

10.系统的单位阶跃响应：系统对单位阶跃信号u(t)的响应称为系统的单位阶跃响应s(t)。

11.傅里叶变换的线性性质：对于信号x(t)和y(t)和常数a和b，有以下性质：a*x(t)+b*y(t)的傅里叶变换为a*X(ω)+b*Y(ω)。

12.傅里叶变换的时移性质：对于信号x(t)，有以下性质：x(t-t0)的傅里叶变换为e^(-jωt0)*X(ω)。

13.周期信号的傅里叶变换：周期信号x(t)的傅里叶变换可以通过傅里叶级数的频谱乘以δ函数的序列得到。

14.采样定理：若连续时间信号x(t)的带宽为BHz，则它的采样频率应大于2BHz，以避免采样失真。

信号频谱计算公式一、信号频谱的概念与意义在信号处理中，信号频谱表示信号在不同频率下的幅度和相位信息。

通过信号频谱，我们可以了解信号的频率成分，以及各频率成分的幅度和相位关系。

信号频谱对于通信、音频处理、图像处理等领域具有重要意义，因为它能帮助我们分析信号的特性，为后续的处理和设计提供依据。

二、傅里叶变换与信号频谱计算傅里叶变换是计算信号频谱的核心方法。

对于连续时间信号x(t)，其傅里叶变换X(f)定义为：X(f) = ∫x(t) * e^(-j2πft) dt其中，f表示频率，j为虚数单位。

通过傅里叶变换，我们可以将时域信号转换到频域，得到信号的频谱。

对于离散时间信号x[n]，我们通常使用离散傅里叶变换（DFT）计算其频谱：X[k] = ∑x[n] * e^(-j2πkn/N)其中，k表示频率索引，N为信号长度。

DFT是计算离散信号频谱的基础工具，但其计算复杂度较高。

为提高计算效率，人们发展了快速傅里叶变换（FFT）算法，极大地减少了计算量。

三、信号频谱分析与应用1.通信领域：在通信系统中，信号频谱用于分析信道的频率响应，以及信号的调制和解调。

通过信号频谱，我们可以设计滤波器、均衡器等器件，优化通信性能。

2.音频处理：音频信号的频谱分析可以帮助我们了解声音的频率成分，实现音频的压缩、降噪、均衡等处理。

例如，MP3压缩算法就利用了人耳对音频频谱的感知特性，实现了高压缩比下的音质保持。

3.图像处理：图像可以看作二维信号，因此信号频谱分析方法也可用于图像处理。

在图像处理中，频谱分析可用于图像的压缩、去噪、增强等操作。

例如，JPEG压缩算法就利用了图像的频谱特性，实现了图像的高效压缩。

四、信号频谱计算的注意事项1.窗函数选择：在实际的信号频谱计算中，为减小泄漏效应和提高频谱分辨率，通常需要选择合适的窗函数对信号进行加窗处理。

常用的窗函数有矩形窗、汉宁窗、海明窗等。

2.采样定理：在计算信号频谱时，需要遵循采样定理，确保采样频率高于信号最高频率的两倍，以避免频谱混叠。