材料力学习题第六章应力状态分析答案详解
- 格式:docx
- 大小:957.25 KB
- 文档页数:28

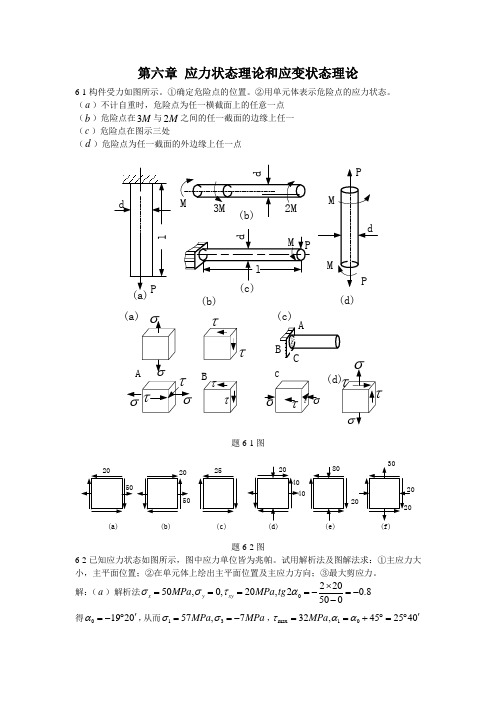
第6章 应力状态分析一、选择题1、对于图示各点应力状态,属于单向应力状态的是(A )。
20(MPa )20d(A )a 点;(B )b 点;(C )c 点;(D )d 点 。
2、在平面应力状态下,对于任意两斜截面上的正应力αβσσ=成立的充分必要条件,有下列四种答案,正确答案是( B )。
(A ),0x y xy σστ=≠;(B ),0x y xy σστ==;(C ),0x y xy σστ≠=;(D )x y xy σστ==。
3、已知单元体AB 、BC 面上只作用有切应力τ,现关于AC 面上应力有下列四种答案,正确答案是( C )。
(A )AC AC /2,0ττσ==; (B )AC AC /2,/2ττσ==;(C )AC AC /2,/2ττσ==;(D )AC AC /2,/2ττσ=-=。
4、矩形截面简支梁受力如图(a )所示,横截面上各点的应力状态如图(b )所示。
关于它们的正确性,现有四种答案,正确答案是( D )。
(b)(a)(A )点1、2的应力状态是正确的;(B )点2、3的应力状态是正确的;(C )点3、4的应力状态是正确的;(D )点1、5的应力状态是正确的。
5、对于图示三种应力状态(a )、(b )、(c)之间的关系,有下列四种答案,正确答案是( D )。
τ(a)(b)(c)(A )三种应力状态均相同;(B )三种应力状态均不同;(C )(b )和(c )相同; (D )(a )和(c )相同;6、关于图示主应力单元体的最大切应力作用面有下列四种答案,正确答案是( B )。
(A)(B)(D)(C)解答:max τ发生在1σ成45的斜截面上7、广义胡克定律适用范围,有下列四种答案,正确答案是( C )。
(A )脆性材料;(B )塑性材料;(C )材料为各向同性,且处于线弹性范围内;(D )任何材料;8、三个弹性常数之间的关系:/[2(1)]G E v =+ 适用于( C )。


第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( ) 1.2 内力只作用在杆件截面的形心处。
( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( ) 1.4 确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ) 1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ) 1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。
( ) 1.8 同一截面上各点的正应力σ必定大小相等,方向相同。
( ) 1.9 同一截面上各点的切应力τ必相互平行。
( ) 1.10 应变分为正应变ε和切应变γ。
( ) 1.11 应变为无量纲量。
( ) 1.12 若物体各部分均无变形,则物体内各点的应变均为零。
( ) 1.13 若物体内各点的应变均为零,则物体无位移。
( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( )1.15 题1.15图所示结构中,AD 杆发生的变形为弯曲与压缩的组合变形。
( ) 1.16 题1.16图所示结构中,AB 杆将发生弯曲与压缩的组合变形。
( )二、填空题1.1 材料力学主要研究 受力后发生的 ,以及由此产生的 。
1.2 拉伸或压缩的受力特征是 ,变形特征是 。
1.3 剪切的受力特征是 ,变形特征是 。
1.4 扭转的受力特征是 ,变形特征是 。
B题1.15图题1.16图1.5 弯曲的受力特征是 ,变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 , 和 三个方面。
1.8 所谓 ,是指材料或构件抵抗破坏的能力。
所谓 ,是指构件抵抗变形的能力。
所谓 ,是指材料或构件保持其原有平衡形式的能力。
1.9 根据固体材料的性能作如下三个基本假设 , , 。


材料力学性能课后习题答案第一章单向静拉伸力学性能1、解释下列名词。
1弹性比功:金属材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
2.滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
3.循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
4.包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
5.解理刻面:这种大致以晶粒大小为单位的解理面称为解理刻面。
6.塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
脆性:指金属材料受力时没有发生塑性变形而直接断裂的能力韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。
7.解理台阶:当解理裂纹与螺型位错相遇时,便形成一个高度为b的台阶。
8.河流花样:解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。
是解理台阶的一种标志。
9.解理面:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似,故称此种晶体学平面为解理面。
10.穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
11.韧脆转变:具有一定韧性的金属材料当低于某一温度点时,冲击吸收功明显下降,断裂方式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变2、说明下列力学性能指标的意义。
答:E 弹性模量 G 切变模量 r σ规定残余伸长应力 2.0σ屈服强度 gt δ金属材料拉伸时最大应力下的总伸长率 n 应变硬化指数 P15 3、 金属的弹性模量主要取决于什么因素?为什么说它是一个对组织不敏感的力学性能指标?答:主要决定于原子本性和晶格类型。
合金化、热处理、冷塑性变形等能够改变金属材料的组织形态和晶粒大小,但是不改变金属原子的本性和晶格类型。
1. 有一拉伸试样,横截面为40mm 5mm ⨯的矩形。
在与轴线成45α︒=角的面上切应力150MPa τ=时,试样上将出现滑移线。
求试样所受的轴向拉力F 的数值。
(C) 解:1). 轴向拉伸杆任意斜截面上切应力公式0sin 2sin 222F Aασταα==2). 求轴向拉力F()6220.040.00515010sin 2sin 24(N)5 60000N=60kNA F ατα︒⨯⨯⨯⨯==⨯=yτA 2解:1).根据单元体上已知应力作应力圆,可得122x yx yOC CE CA σσσσ+=--==2). 求E 点坐标所对应的截面上的正应力和切应力()()cos2 cos222sin2sin22x yx yx yOF OC CF OC CE EF CE αασασσσσασσταα=-=--=--+-=+-===3. 试用应力圆的几何关系求图示悬臂梁距离自由端为0.72m 的截面上,在顶面以下40mm 的一点处的最大及最小主应力,并求最大主应力与x 轴之间的夹角。
解:1). 求目标A 点处的正应力A 点处的弯矩:100.727.2kN m M =⨯=3367.2100.04120.080.16 10.5510Pa=10.55MP P a(a)x z M y I σ⨯⨯⨯⨯==⨯=⨯ A 点处的正应力为拉应力,方向见单元体图=10.55MPax2). 求目标A 点处的切应力A 点处的剪力:10kN S F =(方向向上)23222361010120.160.0424420.080.16 0.8810Pa=0.88MPa(Pa)S xy z F h y I τ⎛⎫⎛⎫⨯⨯=-=⨯- ⎪ ⎪⨯⨯⎝⎭⎝⎭=⨯ (根据单元体上切应力的符号规定,该切应力是逆时针,为负) 3). 根据A 点处的单元体绘制应力圆,并求最大、最小主应力作应力圆(注:单元体上右侧面上的切应力为0.88MPa xy τ=-)。
材料⼒学习题第六章应⼒状态分析答案详解第6章应⼒状态分析⼀、选择题1、对于图⽰各点应⼒状态,属于单向应⼒状态的是(A )。
20(MPa )20d20(A )a 点;(B )b 点;(C )c 点;(D )d 点。
2、在平⾯应⼒状态下,对于任意两斜截⾯上的正应⼒αβσσ=成⽴的充分必要条件,有下列四种答案,正确答案是( B )。
(A ),0x y xy σστ=≠;(B ),0x y xy σστ==;(C ),0x y xy σστ≠=;(D )x y xy σστ==。
3、已知单元体AB 、BC ⾯上只作⽤有切应⼒τ,现关于AC ⾯上应⼒有下列四种答案,正确答案是( C )。
(A )AC AC /2,0ττσ==;(B )AC AC /2,/2ττσ==;(C )AC AC /2,/2ττσ==;(D )AC AC /2,/2ττσ=-=。
4、矩形截⾯简⽀梁受⼒如图(a )所⽰,横截⾯上各点的应⼒状态如图(b )所⽰。
关于它们的正确性,现有四种答案,正确答案是( D )。
(b)(a)(A)点1、2的应⼒状态是正确的;(B)点2、3的应⼒状态是正确的;(C)点3、4的应⼒状态是正确的;(D)点1、5的应⼒状态是正确的。
5、对于图⽰三种应⼒状态(a)、(b)、(c)之间的关系,有下列四种答案,正确答案是( D )。
τ(a) (b)(c)(A)三种应⼒状态均相同;(B)三种应⼒状态均不同;(C)(b)和(c)相同;(D)(a)和(c)相同;6、关于图⽰主应⼒单元体的最⼤切应⼒作⽤⾯有下列四种答案,正确答案是( B )。
(A) (B) (D)(C)解答:maxτ发⽣在1σ成45o的斜截⾯上7、⼴义胡克定律适⽤范围,有下列四种答案,正确答案是( C )。
(A)脆性材料;(B)塑性材料;(C)材料为各向同性,且处于线弹性范围内;(D)任何材料;8、三个弹性常数之间的关系:/[2(1)]G E v =+ 适⽤于( C )。
第6章 应力状态分析一、选择题1、对于图示各点应力状态,属于单向应力状态的是(A )。
(A )a 点;(B )b 点;(C )c 点;(D )d 点 。
2、在平面应力状态下,对于任意两斜截面上的正应力αβσσ=成立的充分必要条件,有下列四种答案,正确答案是( B )。
(A ),0x y xy σστ=≠;(B ),0x y xy σστ==;(C ),0x y xy σστ≠=;(D )x y xy σστ==。
3、已知单元体AB 、BC 面上只作用有切应力τ,现关于AC 面上应力有下列四种答案,正确答案是( C )。
(A )AC AC /2,0ττσ==; (B)AC AC /2,/2ττσ==; (C)AC AC /2,/2ττσ==;(D)AC AC /2,/2ττσ=-=。
4、矩形截面简支梁受力如图(a )所示,横截面上各点的应力状态如图(b )所示。
关于它们的正确性,现有四种答案,正确答案是( D )。
(A )点1、2的应力状态是正确的;(B )点2、3的应力状态是正确的;(C )点3、4的应力状态是正确的;(D )点1、5的应力状态是正确的。
5、对于图示三种应力状态(a )、(b )、(c )之间的关系,有下列四种答案,正确答案是( D )。
(A )三种应力状态均相同;(B )三种应力状态均不同; (C )(b )和(c )相同; (D )(a )和(c )相同;6、关于图示主应力单元体的最大切应力作用面有下列四种答案,正确答案是( B )。
解答:max τ发生在1σ成45的斜截面上7、广义胡克定律适用范围,有下列四种答案,正确答案是( C )。
(A )脆性材料;(B )塑性材料;(C )材料为各向同性,且处于线弹性范围内;(D )任何材料; 8、三个弹性常数之间的关系:/[2(1)]G E v =+ 适用于( C )。
(A )任何材料在任何变形阶级; (B )各向同性材料在任何变形阶级; (C )各向同性材料应力在比例极限范围内;(D )任何材料在弹性变形范围内。
解析:在推导公式过程中用到了虎克定律,且G 、E 、v 为材料在比例极限内的材料常数,故适应于各向同性材料,应力在比例极限范围内9、点在三向应力状态中,若312()σνσσ=+,则关于3ε的表达式有以下四种答案,正确答案是( C )。
(A )3/E σ;(B )12()νεε+;(C )0;(D )12()/E νσσ-+。
解析: 10、图示单元体处于纯剪切应力状态,关于045α=方向上和线应变,现有四种答案,正确答案是2(1)E G v =+2(1)EG v =+()()()()3312312312121,10v v E v v E εσσσσσσεσσσσ=-+=+⎡⎤⎣⎦∴=+-+=⎡⎤⎣⎦( C )。
(A )等于零;(B )大于零;(C )小于零;(D )不能确定。
解析:11、图示应力状态,现有四种答案,正确答案是( B )。
(A )0z ε>;(B )0z ε=;(C )0z ε<;(D )不能确定 。
解析: 12、某点的应力状态如图所示,当x σ、y σ、z σ,xy τ增大时,关于z ε值有以下四种答案,正确答案是( A )。
(A )不变;(B )增大;(C )减小;(D )无法判断。
解析: 与xy τ无关13、在图示梁的A 点测得梁在弹性范围内的纵横方向的线应变x ε、y ε后,所能算出的材料常数有( D )。
(A )只有E ;(B )只有 v ;(C )只有G ;(D )E 、v 和G 均可算出。
解析:中间段为纯弯曲,A 点为单向拉伸,则 14、纯剪应力状态下,各向同性材料单元体的体积改变有四种答案,正确答案是( C )。
(A )变大;(B )变小;(C )不变;(D )不一定 。
解析:因纯剪应力状态: 体积改变比能 二、填空题 1、图示单元体属于 单向(拉伸 ) 应力状态。
2、图示梁的A 、B 、C 、D 四点中,单向应力状态的点是 A 、B ,纯剪应力状态的点是 D ,在任何截面上应力均为零的点是 C 。
三、计算题1、求图示单元体的主应力,并在单元体上标出其作用面的位置。
解答:确定1σ 确定3σ2、已知应力状态如图。
试求主应力及其方向角,并确定最大切应力值。
解答:确定1σ 所以090α+确定3σ3、图示单元体,求:(1)指定斜截面上的应力:(2)主应力大小,并将主平面标在单元体图上。
解答:()33121110xy xy xy vv v E E Eεσσστττ+⎡⎤=-+=--=<⎡⎤⎣⎦⎣⎦()2312110()0z xy xy v v E E εεσσσττ⎡⎤==-+=--=⎡⎤⎣⎦⎣⎦()1z z x y v E εσσσ⎡⎤=-+⎣⎦,2(1)y x X x x zv Fa yE I EG v εεσσε=-∙===+()123123,0,1212(0)0600r r v v V E E V V VV στσστσσσττ===---∴=++=+-=∆∴==∴∆=60200,200,300,604001cos 2sin 20cos120300sin120200300159.82222x y xy x yx yxy x yMpa Mpa Mpa σστασσσσσατασσ==-=-=+-=+-=++=-∙+=-确定1σ 所以090α+确定3σ4、用解析法求图示单元体ab 面上的应力(030α=),并求max τ及主应力。
解答:5、试求图示单元体主应力及最大切应力,并将主平面在单元体上标出。
解答:0α∴确定1σ,090α+确定3σ6、 物体内某一点,载荷系统Ⅰ和载荷系统Ⅱ单独作用时产生的应力状态分别如图(a )和(b )所示。
试求两载荷系统同时作用时(仍处于弹性小变形)的主单元体和主应力。
解答:7、构件上某点处的应力状态如图所示。
试求该点处的主应力及最大切应力之值,并画出三向应力状态的应力圆。
解答:8、图示单元体,已知40MPa =及该点的最大主应力1120MPa σ=。
求该点的另外两个主应力2σ、3σmax 解答:9、试确定图示单元体的最大切应力,以及图示斜截面上的正应力和切应力。
解答:10、已知受力构件某处的640010x ε-=⨯,50MPa y σ=,40MPa z σ=-,材料的E =200GPa ,v =0.3。
试求该点处的y ε、z ε。
解答:11、图示拉杆,F 、b 、h 以及材料的弹性常数E 、v 均为已知。
试求线段AB 的正应变和转角。
解答:12、求图示梁1—1截面B 点与水平方向成045角方向的线应变045ε。
已知F =10kN ,l =4m ,h =2b=200mm ,E =1×104MPa ,v =0.25。
解答:从s F 、M 图知,由于B 点在中性轴上,故为纯剪应力状态,对于纯剪应力状态,有: 13、空心圆轴外径D =8cm ,内径d =6cm ,两端受外力偶矩m 作用。
测得表面上一点沿045方向的线应变53410ε-=-⨯。
材料弹性模量E =2×105MPa ,泊松比v =0.3,求外力偶矩m 。
解答: 纯剪应力状态,则:14、一个处于二向应力状态下的单元体,材料E =200GPa ,v =0.3,170MPa σ=,370MPa σ=-。
求最大切应变max γ。
解答:15、圆轴直径为d ,材料的弹性模量为E ,泊松比为v ,为了测得轴端的力偶m 之值,但只有一枚电阻片。
试设计电阻片粘贴的位置和方向;若按照你所定的位置和方向,已测得线应变为0ε,则m =?()max min77.77.7123max 13}{277.7,7.7,30153.92x y MpaMpaMpa Mpa Mpaσσσσσσστσσ-+=∴==-=-=-=()()245245454545454545cos cos 452cos cos 4521112222122x AB AB v v F v EbhAB AB v F bh AB AB σσσασσσσασσεσσσεεαε--∴==∙===∙-=--⎡⎤=-+=∙=∙⎣⎦∆=⨯⨯∆-====∙()max 34161xy mD ττπα==-解答:(1)电阻片沿图示45方向粘贴于轴的表面,设max ττ= (2)取单元体如图, 16、如图所示,薄壁圆筒受扭矩和轴向力作用。
已知圆筒外径D =52mm ,壁厚t =2mm ,外力偶矩m =600N m ⋅,拉力F =20kN 。
试用单元体表示出D 点的应力状态;求出与母线AB 成030角的斜截面上的应力;求出该点的主应力与主平面位置(并在单元体上画出)。
解答:17、一体积为10×10×10mm 3的立方铝块,将其放入宽为10mm 的刚性槽中,已知v (铝)=0.33,求铝块的三个主应力。
解答:18、外径为D 、内径为d 的空心圆轴受扭转时,若利用一电阻应变片作为测力片,用补偿块作为温度补偿,采用半桥接线。
问:(1)此测力电阻片如何粘贴可测出扭矩;(2)圆轴材料的E 、v 均为已知,ε为测得的应变值,写出扭矩计算式。
解答:(1)电阻片贴在与轴线成沿45方向,设max ττ= (2)取单元体如图,19、一平均半径为R ,壁厚为t (t ≤R /10)的薄壁圆球受内压力p 作用。
已知球体材料的E 、v ,求圆球半径的改变量。
解答:取图示分离体,由经向平衡条件:20、图示单元体,已知材料的弹性模量E =200GPa ,泊松比v =0.25。
求:(1)体积应变;(2)体积改变比能(应变能密度)。
解答: (1) 体积应变 (2) 体积改变比能 21、已知某点的650010x ε-=⨯、640010y ε-=-⨯、620010xy γ-=⨯。
求:(1)与x ε成060面上的060ε;(2)该点的主应变。
解答: 孙书: 李书、刘书: 主应变:第7章 强度理论及其应用一、选择题()()12301123030,0,1111116P v v v E E E E vE d m T w v στσστεεσσστττετεπτ===-+∴==-+=--=∙⎡⎤⎡⎤⎣⎦⎣⎦∴=+∴===∙+()12323124sin 2,021R d Rd t pRd Rd pR tvpR R R R v E Et θσθθθσσσσεσσσ⎛⎫∙∙=∙ ⎪⎝⎭∴====∆==∙-+=-⎡⎤⎣⎦()66412120.253010751020010x y z v E θσσσ---⨯=++=⨯⨯=⨯⨯1、图示应力状态,按第三强度理论校核,强度条件有以下四种答案,正确答案是( D )。