材料力学习题第六章应力状态答案详解.

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。

( ) 1.2 内力只作用在杆件截面的形心处。

( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。

( ) 1.4 确定截面内力的截面法，适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。

( ) 1.5 根据各向同性假设，可认为材料的弹性常数在各方向都相同。

( ) 1.6 根据均匀性假设，可认为构件的弹性常数在各点处都相同。

( ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。

( ) 1.8 同一截面上各点的正应力σ必定大小相等，方向相同。

( ) 1.9 同一截面上各点的切应力τ必相互平行。

( ) 1.10 应变分为正应变ε和切应变γ。

( ) 1.11 应变为无量纲量。

( ) 1.12 若物体各部分均无变形，则物体内各点的应变均为零。

( ) 1.13 若物体内各点的应变均为零，则物体无位移。

( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。

( )1.15 题1.15图所示结构中，AD 杆发生的变形为弯曲与压缩的组合变形。

( ) 1.16 题1.16图所示结构中，AB 杆将发生弯曲与压缩的组合变形。

( )二、填空题1.1 材料力学主要研究 受力后发生的 ，以及由此产生的 。

1.2 拉伸或压缩的受力特征是 ，变形特征是 。

1.3 剪切的受力特征是 ，变形特征是 。

1.4 扭转的受力特征是 ，变形特征是 。

B题1.15图题1.16图1.5 弯曲的受力特征是 ，变形特征是 。

1.6 组合受力与变形是指 。

1.7 构件的承载能力包括 ， 和 三个方面。

1.8 所谓 ，是指材料或构件抵抗破坏的能力。

所谓 ，是指构件抵抗变形的能力。

所谓 ，是指材料或构件保持其原有平衡形式的能力。

1.9 根据固体材料的性能作如下三个基本假设 ， ， 。

材料力学课后习题答案欢迎大家来到大学网，小编搜集整理了材料力学课后习题答案供大家查阅，希望大家喜欢。

1、解释下列名词。

1弹性比功：金属材料吸收弹性变形功的能力，一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。

2.滞弹性：金属材料在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象称为滞弹性，也就是应变落后于应力的现象。

3.循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。

4.包申格效应：金属材料经过预先加载产生少量塑性变形，卸载后再同向加载，规定残余伸长应力增加;反向加载，规定残余伸长应力降低的现象。

5.解理刻面：这种大致以晶粒大小为单位的解理面称为解理刻面。

6.塑性：金属材料断裂前发生不可逆永久(塑性)变形的能力。

韧性：指金属材料断裂前吸收塑性变形功和断裂功的能力。

7.解理台阶：当解理裂纹与螺型位错相遇时，便形成1个高度为b 的台阶。

8.河流花样：解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。

是解理台阶的1种标志。

9.解理面：是金属材料在一定条件下，当外加正应力达到一定数值后，以极快速率沿一定晶体学平面产生的穿晶断裂，因与大理石断裂类似，故称此种晶体学平面为解理面。

10.穿晶断裂：穿晶断裂的裂纹穿过晶内，可以是韧性断裂，也可以是脆性断裂。

沿晶断裂：裂纹沿晶界扩展，多数是脆性断裂。

11.韧脆转变：具有一定韧性的金属材料当低于某一温度点时，冲击吸收功明显下降，断裂方式由原来的韧性断裂变为脆性断裂，这种现象称为韧脆转变12.弹性不完整性：理想的弹性体是不存在的，多数工程材料弹性变形时，可能出现加载线与卸载线不重合、应变滞后于应力变化等现象,称之为弹性不完整性。

弹性不完整性现象包括包申格效应、弹性后效、弹性滞后和循环韧性等决定金属屈服强度的因素有哪些?答：内在因素：金属本性及晶格类型、晶粒大小和亚结构、溶质元素、第二相。

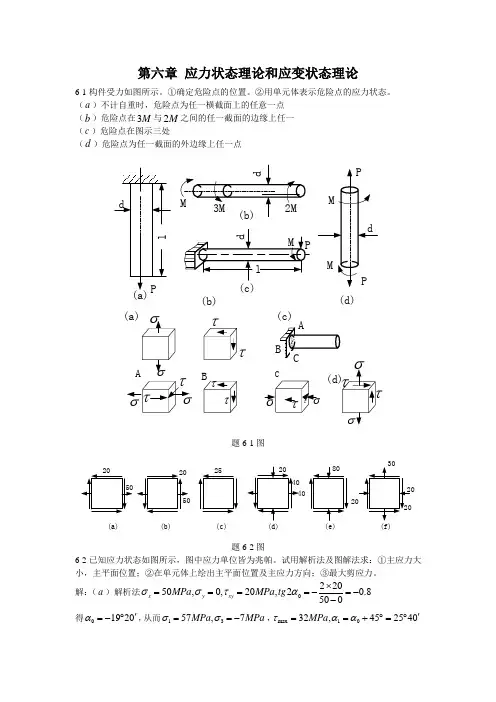
1. 有一拉伸试样，横截面为40mm 5mm ⨯的矩形。

在与轴线成45α︒=角的面上切应力150MPa τ=时，试样上将出现滑移线。

求试样所受的轴向拉力F 的数值。

(C) 解：1). 轴向拉伸杆任意斜截面上切应力公式0sin 2sin 222F Aασταα==2). 求轴向拉力F()6220.040.00515010sin 2sin 24(N)5 60000N=60kNA F ατα︒⨯⨯⨯⨯==⨯=yτA 2解：1).根据单元体上已知应力作应力圆，可得122x yx yOC CE CA σσσσ+=--==2). 求E 点坐标所对应的截面上的正应力和切应力()()cos2 cos222sin2sin22x yx yx yOF OC CF OC CE EF CE αασασσσσασσταα=-=--=--+-=+-===3. 试用应力圆的几何关系求图示悬臂梁距离自由端为0.72m 的截面上，在顶面以下40mm 的一点处的最大及最小主应力，并求最大主应力与x 轴之间的夹角。

解：1). 求目标A 点处的正应力A 点处的弯矩：100.727.2kN m M =⨯=3367.2100.04120.080.16 10.5510Pa=10.55MP P a(a)x z M y I σ⨯⨯⨯⨯==⨯=⨯ A 点处的正应力为拉应力，方向见单元体图=10.55MPax2). 求目标A 点处的切应力A 点处的剪力：10kN S F =(方向向上)23222361010120.160.0424420.080.16 0.8810Pa=0.88MPa(Pa)S xy z F h y I τ⎛⎫⎛⎫⨯⨯=-=⨯- ⎪ ⎪⨯⨯⎝⎭⎝⎭=⨯ (根据单元体上切应力的符号规定，该切应力是逆时针，为负) 3). 根据A 点处的单元体绘制应力圆，并求最大、最小主应力作应力圆(注：单元体上右侧面上的切应力为0.88MPa xy τ=-)。

材料⼒学习题第六章应⼒状态分析答案详解第6章应⼒状态分析⼀、选择题1、对于图⽰各点应⼒状态，属于单向应⼒状态的是（A ）。

20（MPa ）20d20（A ）a 点；（B ）b 点；（C ）c 点；（D ）d 点。

2、在平⾯应⼒状态下，对于任意两斜截⾯上的正应⼒αβσσ=成⽴的充分必要条件，有下列四种答案，正确答案是（ B ）。

（A ）,0x y xy σστ=≠；（B ）,0x y xy σστ==；（C ）,0x y xy σστ≠=；（D ）x y xy σστ==。

3、已知单元体AB 、BC ⾯上只作⽤有切应⼒τ，现关于AC ⾯上应⼒有下列四种答案，正确答案是（ C ）。

（A ）AC AC /2,0ττσ==；（B ）AC AC /2,/2ττσ==；（C ）AC AC /2,/2ττσ==；（D ）AC AC /2,/2ττσ=-=。

4、矩形截⾯简⽀梁受⼒如图（a ）所⽰，横截⾯上各点的应⼒状态如图（b ）所⽰。

关于它们的正确性，现有四种答案，正确答案是（ D ）。

(b)(a)（A）点1、2的应⼒状态是正确的；（B）点2、3的应⼒状态是正确的；（C）点3、4的应⼒状态是正确的；（D）点1、5的应⼒状态是正确的。

5、对于图⽰三种应⼒状态（a）、（b）、（c）之间的关系，有下列四种答案，正确答案是（ D ）。

τ(a) (b)(c)（A）三种应⼒状态均相同；（B）三种应⼒状态均不同；（C）（b）和（c）相同；（D）（a）和（c）相同；6、关于图⽰主应⼒单元体的最⼤切应⼒作⽤⾯有下列四种答案，正确答案是（ B ）。

(A) (B) (D)(C)解答：maxτ发⽣在1σ成45o的斜截⾯上7、⼴义胡克定律适⽤范围，有下列四种答案，正确答案是（ C ）。

（A）脆性材料；（B）塑性材料；（C）材料为各向同性，且处于线弹性范围内；（D）任何材料；8、三个弹性常数之间的关系：/[2(1)]G E v =+ 适⽤于（ C ）。

材料力学(金忠谋)第六版答案第06章(总27页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2弯曲应力6-1 求图示各梁在m －m 截面上A 点的正应力和危险截面上最大正应力。

题 6-1图解：（a ）m KN M m m ⋅=-5.2 m KN M ⋅=75.3max 48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ （压）3 MPa 2.38108.4901051075.3823max =⨯⨯⨯⨯=--σ （b ）m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ （压） MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ （c ）m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ （压） MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D ＝6 cm 的圆轴，其外伸段为空心，内径d ＝4cm ，求轴内最大正应力。

4解：)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。

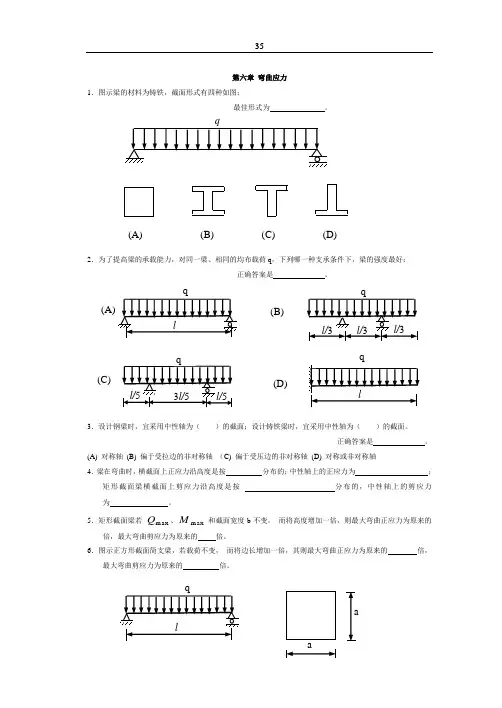
第六章 弯曲应力1．图示梁的材料为铸铁，截面形式有四种如图：最佳形式为 。

2．为了提高梁的承载能力，对同一梁、相同的均布载荷q ，下列哪一种支承条件下，梁的强度最好： 正确答案是 。

3．设计钢梁时，宜采用中性轴为（ ）的截面；设计铸铁梁时，宜采用中性轴为（ ）的截面。

正确答案是 。

(A) 对称轴 (B) 偏于受拉边的非对称轴 （C) 偏于受压边的非对称轴 (D) 对称或非对称轴4．梁在弯曲时，横截面上正应力沿高度是按 分布的；中性轴上的正应力为 ；矩形截面梁横截面上剪应力沿高度是按 分布的，中性轴上的剪应力为 。

5．矩形截面梁若max Q 、m ax M 和截面宽度b 不变， 而将高度增加一倍，则最大弯曲正应力为原来的倍，最大弯曲剪应力为原来的 倍。

6．图示正方形截面简支梁，若载荷不变， 而将边长增加一倍，其则最大弯曲正应力为原来的 倍，最大弯曲剪应力为原来的 倍。

(A) (B) (C) (D)(C)(B)(D)7．下图所示的梁跨中截面上A 、B 两点的应力A σ= ；A τ= ；B τ= 。

8．图示T 字形截面梁。

若已知A —A 截面上、下表面处沿x 方向的线应变分别是0004.0-='ε，0002.0=''ε，则此截面中性轴位置=c y h （C 为形心）9．铸铁丁字形截面梁的许用应力分别为：许用拉应力 [t σ] = 50MPa ，许用压应力[c σ] = 200 MPa 。

则上下边缘距中性轴的合理比值为 21/y y 为多少？（C 为形心）10．⊥形截面铸铁悬臂梁，尺寸及载荷如图所示。

若材料的拉伸许用应力[]MPa l 40=σ，压缩许用应力[]MPa c 160=σ，截面对形心轴z c的惯性矩410180cm zc=I ，cm h 64.91=，试计算该梁的许可载荷P 。

11．正方形截面简支梁，受有均布载荷作用如图，若[σ] = 6 [τ] ，证明当梁内最大正应力和最大剪应力同时达到许用应力时，l / a = 6xA-ABc12．铸铁制梁的尺寸及所受载荷如图所示。

材料力学课后答案材料力学是研究材料内部力学性质和行为的学科，它是材料科学与工程学的重要基础课程之一。

通过学习材料力学，我们可以了解材料的力学性能和行为，为材料的设计、加工和应用提供理论基础和指导。

在课堂学习之外，课后习题是巩固知识、提高能力的重要途径。

下面是一些材料力学课后习题的答案，希望能对大家的学习有所帮助。

1. 什么是应力？应变？它们之间的关系是什么？答，应力是单位面积上的力，通常用σ表示，其公式为σ=F/A，其中F为作用在物体上的力，A为物体的受力面积。

应变是物体单位长度的形变，通常用ε表示，其公式为ε=ΔL/L0，其中ΔL为长度变化量，L0为原始长度。

应力和应变之间的关系由杨氏模量E来描述，公式为σ=Eε。

2. 什么是弹性模量？它有哪些类型？答，弹性模量是描述材料在弹性阶段的刚度和变形能力的物理量。

常见的弹性模量包括杨氏模量、剪切模量、泊松比等。

3. 什么是拉伸、压缩、剪切？答，拉伸是指物体在外力作用下沿着其长度方向发生的形变；压缩是指物体在外力作用下沿着其长度方向发生的缩短形变；剪切是指物体在外力作用下沿着其平面内部发生的相对位移形变。

4. 什么是胶性变形？塑性变形？答，胶性变形是指材料在受力作用下发生的可逆形变，即在去除外力后，材料可以恢复到原来的形状；塑性变形是指材料在受力作用下发生的不可逆形变，即在去除外力后，材料无法完全恢复到原来的形状。

5. 什么是材料的疲劳破坏？有哪些影响因素？答，材料的疲劳破坏是指在交变应力作用下，材料在循环载荷下发生的破坏。

影响因素包括应力幅值、载荷次数、材料的强度和韧性等。

以上是对材料力学课后习题的部分答案，希望能够帮助大家更好地理解和掌握材料力学的知识。

在学习过程中，要多做习题、多思考、多讨论，相信通过努力，一定能够取得好成绩。

习 题第六章 拉伸与压缩变形6-1 试求图6-32所示各杆横截面1-1、2-2、3-3上的轴力，并画出轴力图。

(a)解：01=N F , KN F N 22= , KN F N 33-=(b)解：KN F N 501=, KN F N 102= , KN F N 203-=(c)解：KN F N 21=, KN F N 62=(d)解：01=N F , F F N 42= , F F N 33=6-2 如图6-33所示，一正中开槽的直杆，承受轴向载荷F=40kN 的作用。

已知h=30mm ，h 0=10mm b=25mm 。

试求杆内1—1、2—2截面上的应力。

解：（1）求各截面的轴力：KN F F F N N 4021-=-==（压力）（2）求各截面的面积：217503025.mm h b A =⨯==202500)1030(25)(mm h h b A =-⨯=-=（3）求各截面上的应力：MPa A F N 3.5375010403111=⨯==σ（压应力）MPa A F N 8050010403222=⨯==σ（压应力）6-3 如图6-34所示支架，在节点B 处悬挂一重量G=20kN 的重物，杆AB 及BC 均为圆截面铅制件。

已知杆AB 的直径为d 1=20mm ,杆BC 的直径为d 2=40mm ，杆的许用应力[σ]=160MPa 。

试校核支架的强度。

解：（1）求两杆内力用截面法，将AB 、BC 杆截开，AB 杆内力为1N F ，BC 杆内力为2N F ，取B 为研究对象，由KN G G F N 40230sin 02===（压力） KN F F N N 64.34866.04030cos 021=⨯=⋅=（拉力）（2）求两杆横截面面积2221131442014.34mm d A =⨯=⋅=π 22222125644014.34mm d A =⨯=⋅=π （3）求两杆应力MPa A F N 1103141064.343111=⨯==σ（拉应力） MPa A F N 8.31125610403222=⨯==σ（压应力） （4）校核两杆强度因1σ＜[]σ ， 2σ＜[]σ所以两杆强度均足够。

第六弯曲应力第六章答案6.1钢丝直径d=0.4mm, 弹性模量E=200GPa, 若将钢丝弯成直径D=400mm 的圆弧时，试求钢丝横截面上的最大弯曲正应力。

（200MPa ） 解：钢丝的弯矩和中性层曲率半径之间的关系为：EIM =ρ1则： ρEIM =，由弯曲正应力公式得ρσmaxmax My ==ρmaxEy ，钢丝弯成圆弧后，产生的弯曲变形，其中性层的曲率半径22Dd D ≈+=ρ 2)2(maxD dE =σ==D Ed MPa 2004004.0102003=⨯⨯6.2 矩形截面梁如图所示。

b = 8cm, h =12cm, 试求危险截面上a 、c 、d 三点的弯曲正应力。

（20.8MPa, 10.4MPa, 0） 解：由平衡方程0)(=∑F M A得到： KN F F B A 44221=⨯⨯== 危险截面在梁的中点处：KNm ql M 442818122max =⨯⨯==I z =1212h b ⨯⨯=44310115212080121mm ⨯=⨯⨯MP a I My MPa I MyI My z d d z c c za a 83.201011526010442.101011523010404646=⨯⨯⨯===⨯⨯⨯====σσσA F BF s F MM机械土木6.3 从直径为d 的圆木中截取一矩形截面梁，试根据强度观点求出所截取的矩形截面的最合理的高h 和宽b 。

(h=d 36, b=d 33) 解：最大弯曲正应力：zz W My I M m a x m a x m a x m a x ==σ h/b 的最佳值应应使梁的抗弯截面系数为最大。

抗弯截面系数： )(61)(616132222b b d b d b bh W -=-==为b 为自变量的函数。

由 06322=-=b d dt dW 36 333222db d h d d b =-===6.4 图示两根简支梁，其跨度、荷载及截面面积都相同。

材料力学 分析与思考题集第一章 绪论和基本概念一、选择题1.关于确定截面内力的截面法的适用范围，有下列四种说法：【D.适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普通情况。

2.关于下列结论的正确性：【C 1.同一截面上正应力τσ与剪应力必须相互垂直3.同一截面上各点的剪应力必相互平行。

】3.下列结论中那个是正确的：【B.若物体各点均无位移，则该物体必定无变形】4.根据各向同性假设，可认为构件的下列量中的某一种量在各方向都相同：【B 材料的弹性常数】5.根据均匀性假设，可认为构件的下列量中的某个量在各点处都相同：【C 材料的弹性常数】6.关于下列结论：【C 1.应变分为线应变ε和切应变γ 2.应变为无量纲量 3.若物体的各部分均无变形，则物体内各点的应变均为零】7.单元体受力后，变形如图虚线所示，则切应变γ为【B 2α】二、填空题1.根据材料的主要性能作如下三个基本假设 连续性假设 ， 均匀性假设 和 各向同性假设 。

2.构件的承载能力包括强度、刚度和稳定性三个方面。

3.图示结构中，杆1发生轴向拉伸变形，杆2发生轴向压缩变形，杆3发生弯曲变形。

4.图示为构件内A 点处取出的单元体，构件受力后单元体的位置为虚线表示，则称dx du /为A 点沿x 方向的线应变，dy dv /为【A 点沿y 方向的线应变】，)(21a a +为【A 在xy 平面内的角应变】。

5.认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为连续性假设。

根据这一假设，构件的应力、应变和位移就可以用坐标的连续性函数来表示。

6.在拉（压）杆斜截面上某点处分布内力集度称为应力(或全应力），它沿着截面法线方向的分量称为正应力，而沿截面切线方向的分量称为切应力。

第二章 杆件的内力分析一、选择题1.单位宽度的薄壁圆环受力如图所示，p 为径向压强，其n-n 截面上的内力N F 有四个答案：【B 2/pD 】2.梁的内力符号与坐标系的关系是：【B 剪力、弯矩符号与坐标系无关】3.梁的受载情况对于中央截面为反对称（如图）。