材料力学习题第六章应力状态分析答案详解

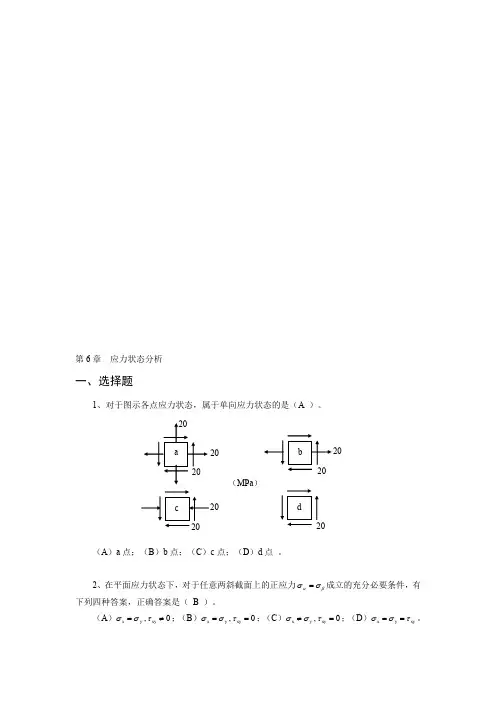
第6章 应力状态分析一、选择题1、对于图示各点应力状态，属于单向应力状态的是（A ）。

20（MPa ）20d（A ）a 点；（B ）b 点；（C ）c 点；（D ）d 点 。

2、在平面应力状态下，对于任意两斜截面上的正应力αβσσ=成立的充分必要条件，有下列四种答案，正确答案是（ B ）。

（A ）,0x y xy σστ=≠；（B ）,0x y xy σστ==；（C ）,0x y xy σστ≠=；（D ）x y xy σστ==。

3、已知单元体AB 、BC 面上只作用有切应力τ，现关于AC 面上应力有下列四种答案，正确答案是（ C ）。

（A ）AC AC /2,0ττσ==； （B ）AC AC /2,/2ττσ==；（C ）AC AC /2,/2ττσ==；（D ）AC AC /2,/2ττσ=-=。

4、矩形截面简支梁受力如图（a ）所示，横截面上各点的应力状态如图（b ）所示。

关于它们的正确性，现有四种答案，正确答案是（ D ）。

(b)(a)（A ）点1、2的应力状态是正确的；（B ）点2、3的应力状态是正确的；（C ）点3、4的应力状态是正确的；（D ）点1、5的应力状态是正确的。

5、对于图示三种应力状态（a ）、（b ）、（c）之间的关系，有下列四种答案，正确答案是（ D ）。

τ(a)(b)(c)（A ）三种应力状态均相同；（B ）三种应力状态均不同；（C ）（b ）和（c ）相同； （D ）（a ）和（c ）相同；6、关于图示主应力单元体的最大切应力作用面有下列四种答案，正确答案是（ B ）。

(A)(B)(D)(C)解答：max τ发生在1σ成45的斜截面上7、广义胡克定律适用范围，有下列四种答案，正确答案是（ C ）。

（A ）脆性材料；（B ）塑性材料；（C ）材料为各向同性，且处于线弹性范围内；（D ）任何材料；8、三个弹性常数之间的关系：/[2(1)]G E v =+ 适用于（ C ）。

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。

( ) 1.2 内力只作用在杆件截面的形心处。

( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。

( ) 1.4 确定截面内力的截面法，适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。

( ) 1.5 根据各向同性假设，可认为材料的弹性常数在各方向都相同。

( ) 1.6 根据均匀性假设，可认为构件的弹性常数在各点处都相同。

( ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。

( ) 1.8 同一截面上各点的正应力σ必定大小相等，方向相同。

( ) 1.9 同一截面上各点的切应力τ必相互平行。

( ) 1.10 应变分为正应变ε和切应变γ。

( ) 1.11 应变为无量纲量。

( ) 1.12 若物体各部分均无变形，则物体内各点的应变均为零。

( ) 1.13 若物体内各点的应变均为零，则物体无位移。

( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。

( )1.15 题1.15图所示结构中，AD 杆发生的变形为弯曲与压缩的组合变形。

( ) 1.16 题1.16图所示结构中，AB 杆将发生弯曲与压缩的组合变形。

( )二、填空题1.1 材料力学主要研究 受力后发生的 ，以及由此产生的 。

1.2 拉伸或压缩的受力特征是 ，变形特征是 。

1.3 剪切的受力特征是 ，变形特征是 。

1.4 扭转的受力特征是 ，变形特征是 。

B题1.15图题1.16图1.5 弯曲的受力特征是 ，变形特征是 。

1.6 组合受力与变形是指 。

1.7 构件的承载能力包括 ， 和 三个方面。

1.8 所谓 ，是指材料或构件抵抗破坏的能力。

所谓 ，是指构件抵抗变形的能力。

所谓 ，是指材料或构件保持其原有平衡形式的能力。

1.9 根据固体材料的性能作如下三个基本假设 ， ， 。

材料力学性能课后习题答案第一章单向静拉伸力学性能1、解释下列名词。

1弹性比功：金属材料吸收弹性变形功的能力，一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。

2．滞弹性：金属材料在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象称为滞弹性，也就是应变落后于应力的现象。

3．循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。

4．包申格效应：金属材料经过预先加载产生少量塑性变形，卸载后再同向加载，规定残余伸长应力增加；反向加载，规定残余伸长应力降低的现象。

5．解理刻面：这种大致以晶粒大小为单位的解理面称为解理刻面。

6．塑性：金属材料断裂前发生不可逆永久（塑性）变形的能力。

脆性：指金属材料受力时没有发生塑性变形而直接断裂的能力韧性：指金属材料断裂前吸收塑性变形功和断裂功的能力。

7.解理台阶：当解理裂纹与螺型位错相遇时，便形成一个高度为b的台阶。

8.河流花样：解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。

是解理台阶的一种标志。

9.解理面：是金属材料在一定条件下，当外加正应力达到一定数值后，以极快速率沿一定晶体学平面产生的穿晶断裂，因与大理石断裂类似，故称此种晶体学平面为解理面。

10.穿晶断裂：穿晶断裂的裂纹穿过晶内，可以是韧性断裂，也可以是脆性断裂。

沿晶断裂：裂纹沿晶界扩展，多数是脆性断裂。

11.韧脆转变：具有一定韧性的金属材料当低于某一温度点时，冲击吸收功明显下降，断裂方式由原来的韧性断裂变为脆性断裂，这种现象称为韧脆转变2、说明下列力学性能指标的意义。

答：E 弹性模量 G 切变模量 r σ规定残余伸长应力 2.0σ屈服强度 gt δ金属材料拉伸时最大应力下的总伸长率 n 应变硬化指数 P15 3、 金属的弹性模量主要取决于什么因素？为什么说它是一个对组织不敏感的力学性能指标？答：主要决定于原子本性和晶格类型。

合金化、热处理、冷塑性变形等能够改变金属材料的组织形态和晶粒大小，但是不改变金属原子的本性和晶格类型。

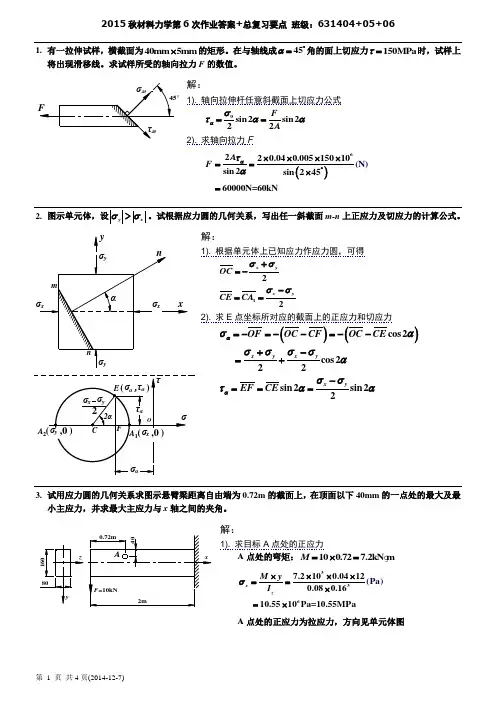
1. 有一拉伸试样，横截面为40mm 5mm ⨯的矩形。

在与轴线成45α︒=角的面上切应力150MPa τ=时，试样上将出现滑移线。

求试样所受的轴向拉力F 的数值。

(C) 解：1). 轴向拉伸杆任意斜截面上切应力公式0sin 2sin 222F Aασταα==2). 求轴向拉力F()6220.040.00515010sin 2sin 24(N)5 60000N=60kNA F ατα︒⨯⨯⨯⨯==⨯=yτA 2解：1).根据单元体上已知应力作应力圆，可得122x yx yOC CE CA σσσσ+=--==2). 求E 点坐标所对应的截面上的正应力和切应力()()cos2 cos222sin2sin22x yx yx yOF OC CF OC CE EF CE αασασσσσασσταα=-=--=--+-=+-===3. 试用应力圆的几何关系求图示悬臂梁距离自由端为0.72m 的截面上，在顶面以下40mm 的一点处的最大及最小主应力，并求最大主应力与x 轴之间的夹角。

解：1). 求目标A 点处的正应力A 点处的弯矩：100.727.2kN m M =⨯=3367.2100.04120.080.16 10.5510Pa=10.55MP P a(a)x z M y I σ⨯⨯⨯⨯==⨯=⨯ A 点处的正应力为拉应力，方向见单元体图=10.55MPax2). 求目标A 点处的切应力A 点处的剪力：10kN S F =(方向向上)23222361010120.160.0424420.080.16 0.8810Pa=0.88MPa(Pa)S xy z F h y I τ⎛⎫⎛⎫⨯⨯=-=⨯- ⎪ ⎪⨯⨯⎝⎭⎝⎭=⨯ (根据单元体上切应力的符号规定，该切应力是逆时针，为负) 3). 根据A 点处的单元体绘制应力圆，并求最大、最小主应力作应力圆(注：单元体上右侧面上的切应力为0.88MPa xy τ=-)。

材料⼒学习题第六章应⼒状态分析答案详解第6章应⼒状态分析⼀、选择题1、对于图⽰各点应⼒状态，属于单向应⼒状态的是（A ）。

20（MPa ）20d20（A ）a 点；（B ）b 点；（C ）c 点；（D ）d 点。

2、在平⾯应⼒状态下，对于任意两斜截⾯上的正应⼒αβσσ=成⽴的充分必要条件，有下列四种答案，正确答案是（ B ）。

（A ）,0x y xy σστ=≠；（B ）,0x y xy σστ==；（C ）,0x y xy σστ≠=；（D ）x y xy σστ==。

3、已知单元体AB 、BC ⾯上只作⽤有切应⼒τ，现关于AC ⾯上应⼒有下列四种答案，正确答案是（ C ）。

（A ）AC AC /2,0ττσ==；（B ）AC AC /2,/2ττσ==；（C ）AC AC /2,/2ττσ==；（D ）AC AC /2,/2ττσ=-=。

4、矩形截⾯简⽀梁受⼒如图（a ）所⽰，横截⾯上各点的应⼒状态如图（b ）所⽰。

关于它们的正确性，现有四种答案，正确答案是（ D ）。

(b)(a)（A）点1、2的应⼒状态是正确的；（B）点2、3的应⼒状态是正确的；（C）点3、4的应⼒状态是正确的；（D）点1、5的应⼒状态是正确的。

5、对于图⽰三种应⼒状态（a）、（b）、（c）之间的关系，有下列四种答案，正确答案是（ D ）。

τ(a) (b)(c)（A）三种应⼒状态均相同；（B）三种应⼒状态均不同；（C）（b）和（c）相同；（D）（a）和（c）相同；6、关于图⽰主应⼒单元体的最⼤切应⼒作⽤⾯有下列四种答案，正确答案是（ B ）。

(A) (B) (D)(C)解答：maxτ发⽣在1σ成45o的斜截⾯上7、⼴义胡克定律适⽤范围，有下列四种答案，正确答案是（ C ）。

（A）脆性材料；（B）塑性材料；（C）材料为各向同性，且处于线弹性范围内；（D）任何材料；8、三个弹性常数之间的关系：/[2(1)]G E v =+ 适⽤于（ C ）。

材料力学(金忠谋)第六版答案第06章(总27页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2弯曲应力6-1 求图示各梁在m －m 截面上A 点的正应力和危险截面上最大正应力。

题 6-1图解：（a ）m KN M m m ⋅=-5.2 m KN M ⋅=75.3max 48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ （压）3 MPa 2.38108.4901051075.3823max =⨯⨯⨯⨯=--σ （b ）m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ （压） MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ （c ）m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ （压） MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D ＝6 cm 的圆轴，其外伸段为空心，内径d ＝4cm ，求轴内最大正应力。

4解：)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。

材料力学习题册答案第六章材料力学习题册答案第六章材料力学作为工程力学的一个重要分支，研究材料在受力作用下的力学性能和变形行为。

在学习过程中，习题册是一个很好的辅助工具，能够帮助我们巩固所学的知识。

本文将为大家提供材料力学习题册第六章的答案，希望能够对大家的学习有所帮助。

第六章主要涉及材料的应变和应力分析，包括平面应变和平面应力的分析方法。

在这一章中，我们将学习如何计算材料在受力作用下的应变和应力分布，以及如何通过应变和应力分布来判断材料的强度和稳定性。

在第六章的习题中，我们会遇到一些典型的问题，例如平面应变和平面应力的计算，应变和应力的变换关系，以及应力的主方向和主应力的计算等。

以下是一些典型问题的答案，供大家参考：1. 一个长方形钢板的尺寸为20cm×30cm，厚度为5mm。

当该钢板受到拉伸力为5000N时，求钢板上的应力分布。

答案：首先计算钢板的截面积，即20cm×30cm=600cm²=0.06m²。

然后应力等于受力除以截面积，即5000N/0.06m²=83333.33Pa。

因此钢板上的应力分布为83333.33Pa。

2. 一个正方形钢材的尺寸为10cm×10cm，厚度为2mm。

当该钢材受到压力为2000N/m²时，求钢材上的应变分布。

答案：首先计算钢材的截面积，即10cm×10cm=100cm²=0.01m²。

然后应变等于受力除以截面积，即2000N/m²/0.01m²=200000。

因此钢材上的应变分布为200000。

3. 一个矩形钢板的尺寸为30cm×40cm，厚度为5mm。

当该钢板受到拉伸力为10000N时，求钢板上的最大应力和最小应力。

答案：首先计算钢板的截面积，即30cm×40cm=1200cm²=0.12m²。

然后最大应力等于受力除以截面积，即10000N/0.12m²=83333.33Pa。

材料力学 分析与思考题集第一章 绪论和基本概念一、选择题1.关于确定截面内力的截面法的适用范围，有下列四种说法：【D.适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普通情况。

2.关于下列结论的正确性：【C 1.同一截面上正应力τσ与剪应力必须相互垂直3.同一截面上各点的剪应力必相互平行。

】3.下列结论中那个是正确的：【B.若物体各点均无位移，则该物体必定无变形】4.根据各向同性假设，可认为构件的下列量中的某一种量在各方向都相同：【B 材料的弹性常数】5.根据均匀性假设，可认为构件的下列量中的某个量在各点处都相同：【C 材料的弹性常数】6.关于下列结论：【C 1.应变分为线应变ε和切应变γ 2.应变为无量纲量 3.若物体的各部分均无变形，则物体内各点的应变均为零】7.单元体受力后，变形如图虚线所示，则切应变γ为【B 2α】二、填空题1.根据材料的主要性能作如下三个基本假设 连续性假设 ， 均匀性假设 和 各向同性假设 。

2.构件的承载能力包括强度、刚度和稳定性三个方面。

3.图示结构中，杆1发生轴向拉伸变形，杆2发生轴向压缩变形，杆3发生弯曲变形。

4.图示为构件内A 点处取出的单元体，构件受力后单元体的位置为虚线表示，则称dx du /为A 点沿x 方向的线应变，dy dv /为【A 点沿y 方向的线应变】，)(21a a +为【A 在xy 平面内的角应变】。

5.认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为连续性假设。

根据这一假设，构件的应力、应变和位移就可以用坐标的连续性函数来表示。

6.在拉（压）杆斜截面上某点处分布内力集度称为应力(或全应力），它沿着截面法线方向的分量称为正应力，而沿截面切线方向的分量称为切应力。

第二章 杆件的内力分析一、选择题1.单位宽度的薄壁圆环受力如图所示，p 为径向压强，其n-n 截面上的内力N F 有四个答案：【B 2/pD 】2.梁的内力符号与坐标系的关系是：【B 剪力、弯矩符号与坐标系无关】3.梁的受载情况对于中央截面为反对称（如图）。

第六弯曲应力第六章答案6.1钢丝直径d=0.4mm, 弹性模量E=200GPa, 若将钢丝弯成直径D=400mm 的圆弧时，试求钢丝横截面上的最大弯曲正应力。

（200MPa ） 解：钢丝的弯矩和中性层曲率半径之间的关系为：EIM =ρ1则： ρEIM =，由弯曲正应力公式得ρσmaxmax My ==ρmaxEy ，钢丝弯成圆弧后，产生的弯曲变形，其中性层的曲率半径22Dd D ≈+=ρ 2)2(maxD dE =σ==D Ed MPa 2004004.0102003=⨯⨯6.2 矩形截面梁如图所示。

b = 8cm, h =12cm, 试求危险截面上a 、c 、d 三点的弯曲正应力。

（20.8MPa, 10.4MPa, 0） 解：由平衡方程0)(=∑F M A得到： KN F F B A 44221=⨯⨯== 危险截面在梁的中点处：KNm ql M 442818122max =⨯⨯==I z =1212h b ⨯⨯=44310115212080121mm ⨯=⨯⨯MP a I My MPa I MyI My z d d z c c za a 83.201011526010442.101011523010404646=⨯⨯⨯===⨯⨯⨯====σσσA F BF s F MM机械土木6.3 从直径为d 的圆木中截取一矩形截面梁，试根据强度观点求出所截取的矩形截面的最合理的高h 和宽b 。

(h=d 36, b=d 33) 解：最大弯曲正应力：zz W My I M m a x m a x m a x m a x ==σ h/b 的最佳值应应使梁的抗弯截面系数为最大。

抗弯截面系数： )(61)(616132222b b d b d b bh W -=-==为b 为自变量的函数。

由 06322=-=b d dt dW 36 333222db d h d d b =-===6.4 图示两根简支梁，其跨度、荷载及截面面积都相同。