下载文档原格式
第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( ) 1.2 内力只作用在杆件截面的形心处。
( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( ) 1.4 确定截面内力的截面法，适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ) 1.5 根据各向同性假设，可认为材料的弹性常数在各方向都相同。
( ) 1.6 根据均匀性假设，可认为构件的弹性常数在各点处都相同。
( ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。
( ) 1.8 同一截面上各点的正应力σ必定大小相等，方向相同。
( ) 1.9 同一截面上各点的切应力τ必相互平行。
( ) 1.10 应变分为正应变ε和切应变γ。
( ) 1.11 应变为无量纲量。
( ) 1.12 若物体各部分均无变形，则物体内各点的应变均为零。
( ) 1.13 若物体内各点的应变均为零，则物体无位移。
( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( )1.15 题1.15图所示结构中，AD 杆发生的变形为弯曲与压缩的组合变形。
( ) 1.16 题1.16图所示结构中，AB 杆将发生弯曲与压缩的组合变形。
( )二、填空题1.1 材料力学主要研究 受力后发生的 ，以及由此产生的 。
1.2 拉伸或压缩的受力特征是 ，变形特征是 。
1.3 剪切的受力特征是 ，变形特征是 。
1.4 扭转的受力特征是 ，变形特征是 。
B题1.15图题1.16图1.5 弯曲的受力特征是 ，变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 ， 和 三个方面。
1.8 所谓 ，是指材料或构件抵抗破坏的能力。
所谓 ，是指构件抵抗变形的能力。
所谓 ，是指材料或构件保持其原有平衡形式的能力。
1.9 根据固体材料的性能作如下三个基本假设 ， ， 。
注册土木工程师（港口与航道工程）执业资格考试培训讲稿基础考试：上午4小时120道题每题1分其中材料力学15道题平均每道题用时2分钟。
01年结构考题：拉压2 剪切1 扭转2 截面性质3 弯曲内力2 弯曲正应力3 弯曲变形（含超）2 应力状态强度理论 1 组合变形 2 稳定 102年岩土考题：拉压3 剪切1 扭转2 截面性质2 弯曲内力2 弯曲正应力1 弯曲变形（含超）1 应力状态强度理论 2 组合变形 1 稳定 102年结构考题：拉压3 剪切1 扭转1 截面性质2 弯曲内力2 弯曲正应力2 弯曲变形（含超）1 应力状态强度理论 2 组合变形 1 稳定 2全部是选择题，计算量小根据考试特点复习时应：基本概念要清楚，基本公式和定义要记牢，解题方法要熟练，要培养快速反应能力一、基本概念内力：构件在外力作用下发生变形，引起构件内部各质点之间产生的附加内力（简称内力）。
应力：截面内一点处内力的分布集度。
单位是：N/m2（Pa）、N/mm2（MPa）等。
应力可分为正应力σ和剪应力τ（剪应力）。
位移：构件内任一点由其原来位置到其新位置的连线称为该点的线位移。
构件内某一线段（或平面）由原始位置所转过的角度称为该线段（或平面）的角位移。
变形：构件形状的改变。
应变：构件内任一点处的变形程度。
应变又可分为线应变ε和剪应变γ，均为无量纲量。
线应变ε表示变形前构件内任一点处的一条微线段,变形后的长度改变量与其原始长度之比。
剪应变γ表示过构件内任一点的两个互相垂直的微线段，变形后两个微线段的角度改变量。
例题0 单元体变形后的形状如图中虚线所示，则A点的剪应变是( )。
(A) O，2γ，２γ (B) γ，γ，２γ(C) γ，２γ，２γ (D) O，γ，２γ例题0图答案：D二、四种基本变形的内力、应力及强度、变形1、内力拉压内力：轴力N扭转内力M T弯曲内力Q、M关键点内力的正负号，内力图的画法重点弯曲内力（因拉压、扭转内力较简单）熟练利用剪力、弯矩与分布力的微分关系及其图形的规律判断内力图的正确性。
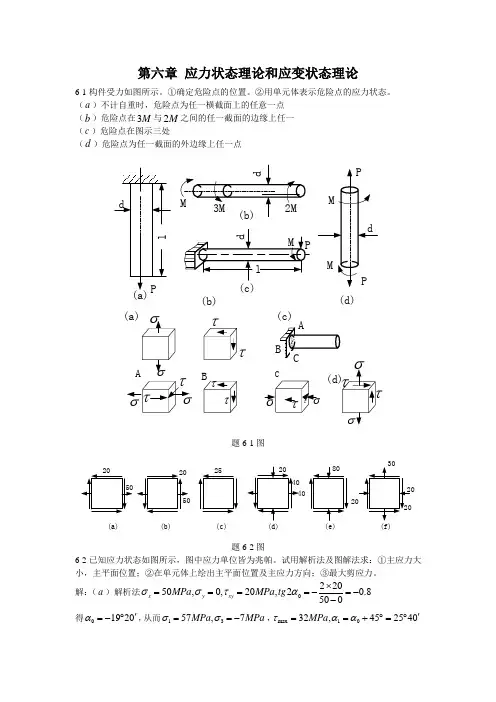
应力、应变状态分析典型习题解析1 已知矩形截面梁，某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。
绘出表示1、2、3及4点应力状态的微体，并求出各点的主应力。
b = 60 mm ，h = 100 mm 。
解题分析：从图中可分析1、4点是单向应力状态，2点在中性轴上为纯剪切应力状态，31取平行和垂直与梁横截面的六个平面，构成微体。
则各点处的应力状态如图示。
2、梁截面惯性矩为点微体上既有正应力又有切应力。
解：、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==）bh I z 1点处弯曲正应力（压应力）MPa 100Pa 10100m10500m 1050m N 101064833−=×=×××⋅×==−−z I My σ1点为单向压缩受力状态，所以021==σσ，MPa 1003−=σ2点为纯剪切应力状态，MPa 30Pa 1030m10100602N1012036263=×=×××××=−τ（向下）容易得到，MPa 301=σ，02=σ，MPa303−=σ3点为一般平面应力状态弯曲正应力MPa50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−z I My σ弯曲切应力σ14τ2F S =120 kN题图1中性轴324hστ25 mm 31b M =10 kN·mσ3150 mm 1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−zz bI S F τMPa6.8MPa6.58Pa)10522()2Pa 1050(2Pa 1050)2(22626622minmax −=×+×±×=+−±+=x y x yx τσσσσσσ所以 MPa 6.581=σ，02=σ，MPa 6.83−=σ4点为单向拉伸应力状态，拉伸正应力的大小与1点相等。
材料力学(金忠谋)第六版答案第06章(总27页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2弯曲应力6-1 求图示各梁在m －m 截面上A 点的正应力和危险截面上最大正应力。
题 6-1图解：（a ）m KN M m m ⋅=-5.2 m KN M ⋅=75.3max 48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ （压）3 MPa 2.38108.4901051075.3823max =⨯⨯⨯⨯=--σ （b ）m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ （压） MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ （c ）m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ （压） MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D ＝6 cm 的圆轴，其外伸段为空心，内径d ＝4cm ，求轴内最大正应力。
4解：)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
材料力学性能-课后答案-(时海芳-任鑫)第一章1.解释下列名词①滞弹性：金属材料在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象称为滞弹性，也就是应变落后于应力的现象。
②弹性比功：金属材料吸收弹性变形功的能力，一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
③循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
④包申格效应：金属材料经过预先加载产生少量塑性变形，卸载后再同向加载，规定残余伸长应力增加；反向加载，规定残余伸长应力降低的现象。
⑤塑性：金属材料断裂前发生不可逆永久（塑性）变形的能力。
⑥韧性：指金属材料断裂前吸收塑性变形功和断裂功的能力。
脆性：指金属材料受力时没有发生塑性变形而直接断裂的能力⑦加工硬化：金属材料在再结晶温度以下塑性变形时,由于晶粒发生滑移, 出现位错的缠结,使晶粒拉长、破碎和纤维化,使金属的强度和硬度升高,塑性和韧性降低的现象。
⑧解理断裂：解理断裂是在正应力作用产生的一种穿晶断裂，即断裂面沿一定的晶面（即解理面）分离。
2.解释下列力学性能指标的意义弹性模量）；（2）ζ p（规定非比例伸长应力）、ζ e（弹性极限）、ζ s（屈服强度）、ζ 0.2（屈服强度）；（3）ζ b（抗拉强度）；（4）n（加工硬化指数）; （5）δ （断后伸长率）、ψ （断面收缩率）4.常用的标准试样有5 倍和10倍，其延伸率分别用δ 5 和δ 10 表示，说明为什么δ 5>δ 10。
答：对于韧性金属材料，它的塑性变形量大于均匀塑性变形量，所以对于它的式样的比例，尺寸越短，它的断后伸长率越大。
5.某汽车弹簧，在未装满时已变形到最大位置，卸载后可完全恢复到原来状态；另一汽车弹簧，使用一段时间后，发现弹簧弓形越来越小，即产生了塑性变形，而且塑性变形量越来越大。
试分析这两种故障的本质及改变措施。
答：（1）未装满载时已变形到最大位置：弹簧弹性极限不够导致弹性比功小；（2）使用一段时间后，发现弹簧弓形越来越小，即产生了塑性变形，这是构件材料的弹性比功不足引起的故障，可以通过热处理或合金化提高材料的弹性极限（或屈服极限），或者更换屈服强度更高的材料。
第6章 应力状态分析一、选择题1、对于图示各点应力状态，属于单向应力状态的是（A ）。
20（MPa ）20d（A ）a 点；（B ）b 点；（C ）c 点；（D ）d 点 。
2、在平面应力状态下，对于任意两斜截面上的正应力αβσσ=成立的充分必要条件，有下列四种答案，正确答案是（ B ）。
（A ）,0x y xy σστ=≠；（B ）,0x y xy σστ==；（C ）,0x y xy σστ≠=；（D ）x y xy σστ==。
3、已知单元体AB 、BC 面上只作用有切应力τ，现关于AC 面上应力有下列四种答案，正确答案是（ C ）。
（A ）AC AC /2,0ττσ==； （B ）AC AC /2,/2ττσ==； （C ）AC AC /2,/2ττσ==；（D ）AC AC /2,/2ττσ=-=。
4、矩形截面简支梁受力如图（a ）所示，横截面上各点的应力状态如图（b ）所示。
关于它们的正确性，现有四种答案，正确答案是（ D ）。
(b)(a)（A）点1、2的应力状态是正确的；（B）点2、3的应力状态是正确的；（C）点3、4的应力状态是正确的；（D）点1、5的应力状态是正确的。
5、对于图示三种应力状态（a）、（b）、（c）之间的关系，有下列四种答案，正确答案是（ D ）。
τ(a)(b) (c)（A）三种应力状态均相同；（B）三种应力状态均不同；（C）（b）和（c）相同；（D）（a）和（c）相同；6、关于图示主应力单元体的最大切应力作用面有下列四种答案，正确答案是（ B ）。
(A) (B) (D)(C)解答：maxτ发生在1σ成45的斜截面上7、广义胡克定律适用围，有下列四种答案，正确答案是（ C ）。
（A）脆性材料；（B）塑性材料；（C）材料为各向同性，且处于线弹性围；（D）任何材料；8、三个弹性常数之间的关系：/[2(1)]G E v=+适用于（ C ）。
（A）任何材料在任何变形阶级；（B）各向同性材料在任何变形阶级；（C）各向同性材料应力在比例极限围；（D）任何材料在弹性变形围。
解析：在推导公式过程中用到了虎克定律，且G 、E 、v 为材料在比例极限的材料常数，故 适应于各向同性材料，应力在比例极限围9、点在三向应力状态中，若312()σνσσ=+，则关于3ε的表达式有以下四种答案，正确答案是（ C ）。
1σ（A ）3/E σ；（B ）12()νεε+；（C ）0；（D ）12()/E νσσ-+。
解析：10、图示单元体处于纯剪切应力状态，关于045α=方向上和线应变，现有四种答案，正确答案是（ C ）。
xy τ（A ）等于零；（B ）大于零；（C ）小于零；（D ）不能确定。
解析：11、图示应力状态，现有四种答案，正确答案是（ B ）。
xy τ（A ）0z ε>；（B ）0z ε=；（C ）0z ε<；（D ）不能确定 。
解析：12、某点的应力状态如图所示，当x σ、y σ、z σ，xy τ增大时，关于z ε值有以下四种答案，正确答案是（ A ）。
2(1)E G v =+2(1)E G v =+()()()()3312312312121,10v v E v v E εσσσσσσεσσσσ=-+=+⎡⎤⎣⎦∴=+-+=⎡⎤⎣⎦()33121110xy xy xy vv v E E Eεσσστττ+⎡⎤=-+=--=<⎡⎤⎣⎦⎣⎦()2312110()0z xy xy v v E E εεσσσττ⎡⎤==-+=--=⎡⎤⎣⎦⎣⎦xz σ（A ）不变；（B ）增大；（C ）减小；（D ）无法判断。
解析： 与xy τ无关13、在图示梁的A点测得梁在弹性围的纵横方向的线应变x ε、y ε后，所能算出的材料常数有（ D ）。
（A ）只有E ；（B ）只有 v ；（C ）只有G ；（D ）E 、v 和G 均可算出。
解析：中间段为纯弯曲，A 点为单向拉伸， 则14、纯剪应力状态下，各向同性材料单元体的体积改变有四种答案，正确答案是（ C ）。
（A ）变大；（B ）变小；（C ）不变；（D ）不一定 。
解析：因纯剪应力状态： 体积改变比能二、填空题()1z z x y v E εσσσ⎡⎤=-+⎣⎦,2(1)y xX x x zv Fa yE I EG v εεσσε=-•===+()123123,0,1212(0)060r r v v V E E V V VV στσστσσσττ===---∴=++=+-=∆∴==∴∆=1、图示单元体属于 单向（拉伸 ） 应力状态。
题1图2、图示梁的A 、B 、C 、D 四点中，单向应力状态的点是 A 、B ，纯剪应力状态的点是 D ，在任何截面上应力均为零的点是 C 。
题2图三、计算题1、求图示单元体的主应力，并在单元体上标出其作用面的位置。
80MPa解答：确定1σ确定3σmax 3min 1115.4455.4412360,0,8060}{22115.44,0,55.44x y xy x yMpaMpa Mpa MpaMpa Mpaσσσσσστσσσσσ-===+∴==∴===-00002280tan 2;34.726034.7290xy x y x y ταασσσσαα⨯=-=-=-->∴=-+2、已知应力状态如图。
试求主应力及其方向角，并确定最大切应力值。
解答：确定1σ 所以090α+确定3σ3、图示单元体，求：（1）指定斜截面上的应力：（2）主应力大小，并将主平面标在单元体图上。
解答：max3min 1102.6252.62123000100,50,2010050}{22102.62,0,52.622220tan 20.2667;7.46100507.46x y xy x yMpaMpaxyx yx y Mpa MpaMpa Mpa σσσσσστσσσσσταασσσσα-==-=+-∴====∴===-⨯=-=-=-=--+>∴=-13max 102.6252.6277.622Mpaσστ-+===max3min 60601200,200,300,604001cos 2sin 20cos120300sin120200300159.82222400sin 2cos 2sin120300cos12032.3222}2x y xy x y x y xy x y xy x yMpa Mpa Mpa Mpa σσσσσστασσσσσατασστατασσ==-=-=+-=+-=++=-•+=-=+=-=+∴==0360.56Mpa±=±确定1σ 所以090α+确定3σ4、用解析法求图示单元体ab 面上的应力（030α=），并求max τ及主应力。
a20MPa解答：5、试求图示单元体主应力及最大切应力，并将主平面在单元体上标出。
解答：max min12340,40,20}44.7244.7,0,44.7x y xy x yMpa Mpa MpaMpa Mpaσσσστσσσσσ==-=+∴=±∴===-max3min6060140,0,204040cos 2sin 2cos12020sin1207.32222240sin 2cos 2sin12020cos1207.322240}22x y xyx y x y xy x y xy x y Mpa MpaMpa Mpaσσσσσστσσσσσατασστατασσ=-==-+-=+-=--+=-=+=--=-+∴===-()8.348.3123max 138.3,0,48.3128.32Mpa MpaMpa Mpa Mpa σσστσσ-=∴===-=-=0α∴确定1σ，090α+确定3σ6、 物体某一点，载荷系统Ⅰ和载荷系统Ⅱ单独作用时产生的应力状态分别如图（a ）和（b ）所示。
试求两载荷系统同时作用时（仍处于弹性小变形）的主单元体和主应力。
(a)解答：7、构件上某点处的应力状态如图所示。
试求该点处的主应力及最大切应力之值，并画出三向应力状态的应力圆。
z解答：8、图示单元体，已知100MPa x σ=、40MPa y σ=及该点的最大主应力1120MPa σ=。
求该点的另外两个主应力2σ、3σ及最大切应力max τ。
()max 13144.72Mpaτσσ=-=()max min77.77.7123max 13}{277.7,7.7,30153.92x yMpaMpaMpa MpaMpa σσσσσσστσσ-+==∴==-=-=-=x解答：9、试确定图示单元体的最大切应力，以及图示斜截面上的正应力和切应力。
解答：10、已知受力构件某处的640010x ε-=⨯，50MPa y σ=，40MPa z σ=-，材料的E ＝200GPa ，v ＝0.3。
试求该点处的y ε、z ε。
解答：()max min4020123max 13}{2120,20,101552x yMpaMpaMpa MpaMpa σσσσσσστσσ+=∴====-=()123max1312303080,40,201502,,0cos 2sin 27022sin 2cos 217.322x y xy x yx yxy x yxy Mpa Mpa Mpaa Mpa MpaMpa σσστσσσσσστσσσσσατασστατα===-∴=-====+-∴=+-=-=+=()()()()()69666140010200100.3504010831185.5101399.510x x y z x x y z y y z x z z y x v E E v Mpav Ev E εσσσσεσσεσσσεσσσ---⎡⎤∴=-+⎣⎦=++=⨯⨯⨯+⨯+-⨯=⎡⎤⎣⎦⎡⎤∴=-+=⨯⎣⎦⎡⎤=-+=-⨯⎣⎦11、图示拉杆，F、b、h以及材料的弹性常数E、v均为已知。
试求线段AB的正应变和转角。
解答:12、求图示梁1—1截面B点与水平方向成045角方向的线应变045ε。
已知F＝10kN，l ＝4m，h＝2b＝200mm，E＝1×104MPa，v＝0.25。
/2/2解答：从sF、M图知，由于B点在中性轴上，故为纯剪应力状态，对于纯剪应力状态，有：()()245245454545454545cos cos452cos cos 4521112222122xABABv v FvE bhABAB v FbhAB ABσσσασσσσασσεσσσεεαε--∴==•===•-=--⎡⎤=-+=•=•⎣⎦∆=⨯⨯∆-====•[]123454535454545454545,0,33310100.37522240.20.11114.9610122B BSBB B BABABF FMpaA h bvv vE E EABAB v FbhAB ABσστσσσττεσστττεεαε---=====-⨯⨯====••⨯⨯⨯+⎡⎤=-=--=-•=-⨯⎣⎦∆=⨯⨯∆-====•13、空心圆轴外径D ＝8cm ，径d ＝6cm ，两端受外力偶矩m 作用。
