当前位置：文档之家 › 单值移动极差

单值移动极差

  • 格式：docx
  • 大小：18.83 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

电流发生器MSA单值-移动极差图

电流发生器MSA单值-移动极差图

移 动 极 差 计 算
mRAvg= 1/g×∑mRj ＝ 0.5172 UCLmR= D4mRAvg ＝ 1.69034 LCLmR= D3mRAvg ＝0
100
4.00 2.00 0.00 -2.00
0.5 1.7 0
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29
95 1 2 3 4 5 6 7 8 9 101112131415161718192021222324252627282930
11
101.2 100.1 100.65 0.20
12
101.1 99பைடு நூலகம்3 100.20 0.45
13
99.9 99.6 99.75 0.45
14
98.9 98.9 98.90 0.85
15
99.2 99.3 99.25 0.35
16
98.2 99.6 98.90 0.35
17
98.9 99.5 99.20 0.30
-4.00
判断准则
不能有点超出控制限
结论
控制图分析显示，测量过程是稳定的，因为没有点明显超过控制限
100±1(mA)
方法描述
因各种原因每次只能得到一个数据或希望尽快发现并消除异常因素时，使用单值移动极差图比较标绘点和控制限并查看趋势。 同一测量装置在每个时间周期从n≥30个样本中，每个样本测量m=1次或多次。 g (j) 1 2
101.2 99.9 100.55 0.40
3
102.1 99.3 100.70 0.15
25
102.1 99.60 100.85 0.85
26
101.5 99.6 100.55 0.30

单值-移动极差控制PPT精选文档

单值-移动极差控制PPT精选文档

4
怎样确定控制限
• X控制图
– 相当于n=2时的均值控制图 CL x MR UCL x 3 x 2.66MR d2 LCL x 3 MR x 2.66MR d2
5
怎样确定控制限
• MR控制图
– 相当于n=2时的极差控制图; – n=2时,D4=3.267,D3=0
CL MR UCL D4MR 3.267MR LCL D3MR 0
6
单值-移动极差控制图（X–MR）
1
单值-移动极差控制图（X–MR）
• 与均值-极差控制图的作用类似； • 不需多个测量值或样本是均匀的（如浓
度）； • 因为费用或时间的关； • 敏感性不强； • 用自动化检查，对产品进行全检时；
2
单值-移动极差图控制限
• 移动极差是指一个测定值 xi 与紧邻的测定 值xi+1 之差的绝对值，记作MR， MRi = | xi - xi+1 | （i=1,2,…,k-1)
– 其中：k为测定值的个数; – k个测定值有k-1个移动极差,每个移动极差值相
当与样本大小n=2时的极差值.
3
怎样确定控制限
• 计算总平均数:
xx1x2... ..x.k k
1k ki1xi
• 计算M R 移 动M 极1 差 平R M 均2 k数 R .1 : . .M ..k .1R k1 1k i 1 1M i R

I-MR(单值-移动极差)控制图解析

I-MR(单值-移动极差)控制图解析

第一个副标题之下。
④脚注 1：键入脚注，该脚注将显示在图形左下方。 ⑤脚注 2：键入第二个脚注，该脚注显示在第一个
脚注之下。
二、操作步骤
设置“标签”后出现的图形。
二、操作步骤
（3）I-MR选项 ①限值 a.标准差的这些倍数：输入一个或多个值，输入后 将在图中显示距离中心线±n个σ的控制限。 在“标准差的这些倍数”后依次输入“1”、“空
14
2 4 15 8
您可以通过更 改 K 值来自定 义特定检验。
二、操作步骤
“检验 1” 用于检测 单个不受 控制的点。 “检验 2” 用于检测 均值可能 出现的偏 移。
二、操作步骤
执行所有的特殊原因 检验：选择此项将进 行所有八项检验。
仅执行选定的特殊原因 不进行检验：选择此项将 检验：要指定八项检验 不执行任何特殊原因检验。 中的部分检验，请选择 此项，然后选中下面所 列检验中的任意几项。
c.设置移动极差控制图控制限的边界
控制限下界：选中此项为移动极差控
制图设置控制限下界，如果设置值大
于计算出的控制下限（LCL) ，会改为
在-3σ处绘制标为下限的水平线。 控制限上界： 选中此项为移动极差控 制图设置控制限上界，如果设置值小 于计算出的控制上限（UCL），会改为
在上+3σ处绘制标上限的水平线。
图中可以看出晶棒外圆直径的平均值为50.943mm，控制限为50.925-50.962mm（标准为50.91-
50.97mm），且样本1-9尺寸波动较大，应去产线查找原因采取措施，以提高产品尺寸的稳定性。
三、分析结果说明
4、在使用 I 控制图之前检查 MR 控制图，确保过程变异是稳定的。 I 控制图上的控制限制基于估计的过程变异（移动极差），如果此过程变 异不稳定，则 I 控制图上的控制限制可能无效。

单值和移动极差图 MR

单值和移动极差图 MR

n 2 3 4 5 6 7 8 9 10 D4 3.27 2.57 2.28 2.11 2.00 1.92 1.86 1.82 1.78 D3 * * * * * 0.08 0.14 0.18 0.22 E2 2.66 1.77 1.46 1.29 1.18 1.11 1.05 1.01 0.98 样本容量小于7时，没有极差的控制下限。 4 过程控制解释（同其他计量型管制图） 5 5 过程能力解释
单值和移动极差图（X—MR）
1、用途 测量费用很大时,(例如破坏性实验）或是当任何时刻点的输出 性质比 较一致时（例如：化学溶液的PH值）。
1-1 移动图的三中用法： a 单值 b 移动组 c 固定子组
2、数据收集（基本同X-R ） 2-1 在数据图上，从左到右记录单值的读数。 2-2 计 算 单 值 间 的 移 动 极 差 （ MR ） ， 通 常 是 记 录 每 对 连 续 读 数 间
的差值 。 2-3 单值图（X）图的刻度按下列最大者选取：
a 产品规范容差加上允许的超出规范的读数。 b 单值的最大值与最小值之差的1.5到2倍。 2-4 移动极差图（MR）的刻度间隔与 X 图一致。
3 计算控制限
USLMR=D4R LSLMR=D3R USLX=X+E2R LSLX=X-E2R
注：式中 R 为移动极差，X 是过程均值，D4、D3 、E2是随样本 容量变化的常数。见下表：
R 为移动极差的均值，d2是随样本容量变化的常数。见下表： n 2 3 4 5 6 7 8 9 10 d2 1.13 1.69 2.06 2.33 2.53 2.70 2.85 2.97 3.08
注： 只有过程受控，才可直接用δ的估计值来评价过程能力。

I-MR(单值-移动极差)控制图

I-MR(单值-移动极差)控制图
结合假设检验
通过假设检验对异常值进行进一步确认，提高控制图的检 测能力。
引入多元统计方法
对于多变量过程，可以采用多元统计方法，如主成分分析 （PCA）或偏最小二乘（PLS）等，对过程进行监控和诊 断。
结合时间序列分析
对于具有时间相关性的过程数据，可以采用时间序列分析 方法，如自回归移动平均（ARMA）模型等，对过程进行 预测和控制。
I-MR控制图假设数据服从正态分布或近似正态分布，若实际数据分布
与假设不符，可能导致控制图失效。
03
无法识别特殊原因的具体性质
当控制图发出异常信号时，I-MR控制图本身无法提供关于异常原因的
具体信息，需要结合其他工具和方法进行进一步分析。
06 I-MR控制图的改 进和发展趋势
结合其他统计方法进行改进
根据预定的公式和移动极差的平均值计算上控制 限。
3
下控制限（LCL）
同样根据预定公式和移动极差的平均值计算下控 制限。
标注数据点和异常情况
标注数据点
01
在控制图上标出每个单值数据点。
异常情况标注
02
如果数据点超出上控制限或下控制限，或者出现非随机的模式
，应标注为异常。
持续监控和更新
03
随着新数据的收集，不断更新控制图，并对异常情况进行跟踪
依据。
03 评估环境治理措施的效果，为政策制定和调整提 供数据支持。
金融市场波动性的研究
分析股票、期货、外 汇等金融市场的价格 波动情况。
辅助制定投资策略， 降低投资风险，提高 投资收益。
评估市场风险，为投 资者提供决策参考。
05 I-MR控制图的优 缺点分析
优点
灵敏度高
I-MR控制图对于过程中的小波动具有较高的灵敏 度，能够迅速发现并提示异常。

单值和移动极差图

单值和移动极差图

单值和移动极差图单值图和移动极差图是两种统计学中常用于探索数据的方法。

它们能够帮助分析人员识别出数据中的异常情况，进而判断某些特定数据是否需要进一步深入研究，以提高数据分析的准确性。

一、单值图单值图主要用于检查数据是否有明显的异常值，即与其他数据相差较大的值。

它通过将每个值单独的绘制在一个图表上进行展示。

这个图表通常包含一个垂直轴和横轴，其中垂直轴表示观测值，而横轴则表示每个观测值对应的编号或时间。

一般来说，单值图呈U型或V型，U型通常表示数据逐渐递减或递增，V型通常表示数据的值在样本中有两个峰值。

单值图可以发现大多数情况下比移动极差图更容易发现数据的异常情况。

如果数据集中的一个观测值与其他观测值差异很大，那么这个值将成为单值图中的异常值，这种情况通常是由数据输入错误、系统故障或人为操作误导等原因引起的。

单值图也可以用于检查数据的分布情况，例如，在数据中是否有噪声，是否具有正态分布的特点等。

二、移动极差图移动极差图则是一种更加普遍使用的方法，它可以用于检查数据是否存在特别高或特别低的变异性。

它通过计算两个连续观测值的极差大小来检查每个数据点的变异性。

移动极差通常在一张图表中显示，其中x轴表示时间或样本点的编号，y轴表示每个移动极差的大小。

一般来说，移动极差图通常呈波浪形状，因为一般移动极差很难完全平滑。

移动极差图通常能够发现数据中的连续或随机变异性，帮助找到数据中的异常情况。

通常，当数据在移动极差图中显示一个很高的峰值，或者当移动极差趋向于在整个样本中变得异常大或异常小，那么这些情况就可能代表了样本中的异常值。

总之，在数据分析中，单值图和移动极差图是常用的探索性方法，可以帮助分析人员识别数据中可能存在的异常情况。

这些方法通常用于前期数据整理、清洗和探索性分析，将帮助构建更加精准和有效的数据分析模型，提高数据分析的准确性。

I-MR(单值-移动极差)控制图


14
2 4 15 8
您可以通过更 改 K 值来自定 义特定检验。
二、操作步骤
“检验 1” 用于检测 单个不受 控制的点。 “检验 2” 用于检测 均值可能 出现的偏 移。
二、操作步骤
执行所有的特殊原因 检验：选择此项将进 行所有八项检验。
仅执行选定的特殊原因 不进行检验：选择此项将 检验：要指定八项检验 不执行任何特殊原因检验。 中的部分检验，请选择 此项，然后选中下面所 列检验中的任意几项。
算出的控制下限（LCL) ，会改为在3σ处绘制标为下限的水平线。 控制限上界：选中此项为单值控制图 设置控制限上界,如果设置值小于计 算出的控制上限（UCL），会改为在 从严显示
如果控制限 上限设置为 50.96＜ UCL(50.962), 则显示为控 制限上限。
+3σ处绘制标为上限的水平线。
二、操作步骤
5、只有在过程变化时才估计新的控制限制。
通常在项目早期阶段的基线分析过程中建立控制限制，如果在项目期间更
改了过程，基线控制限制将不再有效，您必须通过从数据重新估计新的控
制限制来建立它们。建立了控制限制后，它们必须保持固定才能才需要重新估计控制限制，而不 是每次收集新数据时重新估计。
度位置显示网格线。
二、操作步骤
选择“网格线”后出现的图形， 便于查看数据点对应序号或标记。
二、操作步骤
①标题：键入标题，该标题将替换默认标题并在图
（2）标签
形上方居中对齐。
②副标题 1：键入副标题，该副标题显示在标题之 下。如果添加副标题但不添加标题，则副标题会显 示在 Minitab 的默认标题之下。 ③副标题 2：键入第二个副标题，该副标题显示在
图中可以看出晶棒外圆直径的平均值为50.943mm，控制限为50.925-50.962mm（标准为50.91-

I-MR(单值-移动极差)控制图

①时间： 索引：选择此项将用整数标记 X 轴（依次为1、2、3…）。 标记：选择此项可用≤3个标记 列（包含日期/时间、数字或文 本尺度值中的值，首先为最内层） 来标记 X 轴。
选择“索引”后出现的图 形
在“标记”下选择数据对应的日期列，即出 现右图。
②网格线
Y 主刻度：选中此项将在 Y 轴主刻 度位置显示网格线。 Y 小刻度：选中此项将在 Y 轴小刻 度位置显示网格线。 X 主刻度：选中此项将在 X 轴主刻 度位置显示网格线。
不进行检验：选择此项将 不执行任何特殊原因检验。
4、根据需要进行以上设置后，点击“确定”，即生成控制图及会话框。
控制图
会话框
1、上图为单值控制图， Xbar为数据的平 均值。 2、下图为移动极差控制图，每点数据为相 邻数据差的绝对值，MR为各个绝对值的平 均值。 3、1SL、2SL分别为1倍标准差控制限、2倍 标准差控制限，UCL控制上限（3倍标准 差），LCL控制下限（3倍标准差）。
图中可以看出晶棒外圆直径的平均值为50.943mm，控制限为50.925-50.962mm（标准为50.9150.97mm），且样本1-9尺寸波动较大，应去产线查找原因采取措施，以提高产品尺寸的稳定性。
4、在使用 I 控制图之前检查 MR 控制图，确保过程变异是稳定的。 I 控制图上的控制限制基于估计的过程变异（移动极差），如果此过程变 异不稳定，则 I 控制图上的控制限制可能无效。 5、只有在过程变化时才估计新的控制限制。 通常在项目早期阶段的基线分析过程中建立控制限制，如果在项目期间更 改了过程，基线控制限制将不再有效，您必须通过从数据重新估计新的控 制限制来建立它们。建立了控制限制后，它们必须保持固定才能监控过程 或评估过程控制。只有在过程发生变化时才需要重新估计控制限制，而不 是每次收集新数据时重新估计。

单值-移动极差控制..

– 其中：k为测定值的个数; – k个测定值有k-1个移动极差,每个移动极差值相 当与样本大小n=2时的极差值.
怎样确定控制限
• 计算总平均数:
x1 + x2 + ...... + xk 1 k x= = ∑ xi k k i =1
• 计算移动极差平均数: + MR MR1 + MR 2 + ...... k −1
MR = k −1
1 k −1 = ∑ MRi k − 1 i =1
怎样确定控制限
• X控制图
– 相当于n=2时的均值控制图
CL = x MR UCL = x + 3 = x + 2.66MR d2 MR LCL = x − 3 = x − 2.66 MR d2
怎样确定控制限
• MR控制图
– 相当于n=2时的极差控制图; – n=2时,D4=3.267,D3=0
单值-移动极差控制图（X–MR）
单值-移动极差控制图（X–MR）
• 与均值-极差控制图的作用类似； • 不需多个测量值或样本是均匀的（如浓 度）； • 因为费用或时间的关系，过程只有一个测 量值（如破坏性实验）； • 敏感性不强； • 用自动化检查，对产品进行全检时；
单值-移动极差图控制限
• 移动极差是指一个测定值 xi 与紧邻的测定 值xi+1 之差的绝对值，记作MR， MRi = | xi - xi+1 | （i=1,2,…,k-1)
CL = M R UCL = D 4 M R =

单值-移动极差控制

单值-移动极差控制
• 引言 • 单值-移动极差控制原理 • 应用场景 • 案例分析 • 结论
01
引言
目的和背景
目的
单值-移动极差控制是一种用于监测和控制系统动态特性的技术。通过该技术， 可以检测系统的异常行为，并及时采取措施进行纠正。
背景
随着工业自动化和智能化的发展，对系统的稳定性和可靠性要求越来越高。单 值-移动极差控制作为一种有效的监测和控制方法，在许多领域得到了广泛应用。
数据分析
时间序列分析
单值-移动极差可用于时间序列数 据的分析，以揭示数据随时间变 化的趋势和周期性模式。
数据清洗和预处理
在数据分析之前，单值-移动极差 可用于识别和剔除异常值，为后 续的数据分析和建模提供更准确 的数据基础。
数据探索和可视化
结合单值-移动极差分析结果，可 以使用各种可视化工具（如箱线 图、小提琴图等）来展示数据的 分布和变化规律。
VS
局限性
该方法主要适用于具有明显趋势性变化的 过程，对于非线性、时变或随机波动的过 程，单值-移动极差控制可能无法准确反 映过程的真实变化。
对未来研究的建议
进一步优化
01
研究更先进的算法和计算技术，以提高单值-移动极差控制的准
确性和实时性。
扩展应用范围
02
探索单值-移动极差控制在其他领域的应用可能性，如生物过程
04
案例分析
案例一：生产线的质量控制
总结词：有效监控
详细描述：单值-移动极差控制图在生产线质量控制中发挥了重要作用。通过对每个产品进行检查并记录结果，可以及时发现 异常波动，确保产品质量稳定。
案例二：金融市场的数据分析
总结词：风险预警
详细描述：在金融市场数据分析中，单值-移动极差控制图用于监测市场趋势和波动。通过分析数据点 在控制图上的位置和变化趋势，可以预测潜在的市场风险，为投资者提供预警。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第4节
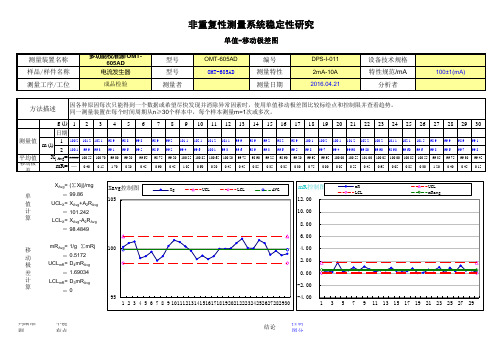
单值和移动极差图（X—MR）
在某些情况下，有必要用单位而不是子组来进行过程控制，在这样的情况下，子组内的变差实际上为0，这种情况通常发生在测量费用很大时（例如破坏性试验），或是当在任何时刻点的输出性质比较一致时（例如：化学溶液的pH值）。

在这些情况下，可按下面介绍的方法绘制单值控制图，但要注意下面4点：
•单值图在检查过程变化时不如X—R图敏感；
•如果过程的分布不是对称的，则在解释单值控制图时要非常小心；
•单值控制图不能区分过程的零件间重复性，因此，在很多情况下，最好还是使用常规的子组样本容量较小（2到4）的X—R控制图，尽管在子组间都要求较长的时间；
•由于每一子组仅有一个单值，X和σ值会有较大的变异性，（即过程是稳定的）直到子组数达到100以上为止。

单值控制图的详细介绍与X—R图有些相同，不同之处如下：A．收集数据（见图27）
（见本章第1节A部分，不同之处如下）
•在数据图上从左至右记录单值读数（X）。

•计算单值间的移动极差（MR）。

通常最好是记录每对连续读数间的差值（例如：第一和第二个读数点的差，第二和第三个读数间的差等）。

这样移动极差的个数比单值读数的个数少一个（25个读数可得到24个移动极差）。

在很少的情况下，可在较大的移动组（例如3或4个（或固定的子组（例如所有的读数均在一个班上读取）的基础上计算移动极差。

注意，尽管测量是单独抽样的，但是读数的个数形成移动极差的成组（例如，2、3或4）决定了各义样本容量n，当查系数表时必须考虑该值；
•单值图（X图）的刻度按下列最大者选取（a）产品的规范容差加上超过规范的读数的允许值，或（b）最大单值读数与最小单值读数之差的1.5到2倍。

移动极差（MR）图的刻度间隔与X图一致。

B．计算控制图
（见本章第1节B部分，不同之处如下）
•计算并描绘过程均值（单值读数之和除以读数的个数，按常规记为X，见附录珠术语，并计算平均极差（R），注意对于样本容量为
2的移动极差，其移动极差（MR）的个数比单值读数的个数少1；
图28 单值和移动极差图的解释（略）
•计算控制限：
UCL MR =D4R
LCL MR=D3 R
UCL X=X+E2R
LCL X=X—E2R
式中：R为移动平均极差，X是过程均值，D4、D3和E2是用来对计算移动极差进行分组，并随样本容量变化的常数，见下面从附录E的表：
注：当R大于中位数极差R时（这种情况常见），另一种计算控制限的方法是，使用样本容量为2的
移动极差的中位数极差，按下式计算控制限（见附录H，参考文献23）：
UCL MR =3.865R̃；LCL MR=0
UCL X=X+3.14R̃；LCL X=X—3.14R
A．过程控制解释（见图28）
（见本章第1节C部分，不同之处如下）
•审查移动极差图中超出控制限的点，这是存在特殊原因的信号。

记住连续的移动极差间是有联系的，因为它们至少有一点是共同的。

由于这个原因，在解释趋势时要特别注意。

对于趋势的解释可能要请教统计学家；
•可用单值图分析超出控制子的点，在控制限内点的分布，以及趋势或图形。

但是这需要注意，如果过程分布不是对称的，用前面所述的用于X图的规则来解释时，可能会给出实际上不存在的特殊原因的信号。

D．过程能力解释
（见本章第1节D部分，不同之处如下）
•与X—R图一样，可用下式估计过程的标准差：
ˆ
σ = R/d2 =σR/d2
式中：R为移动极差的均值，d2是用于对移动极差分组的随样本容量n而变化的常数，见下面从附录E摘录的部分表：
•如果过程处于正态分布，只要过程处于统计控制状态，就可直接用σ的估计值业评价过程能力。