5-3频率域稳定判据
- 格式:ppt
- 大小:671.00 KB
- 文档页数:26


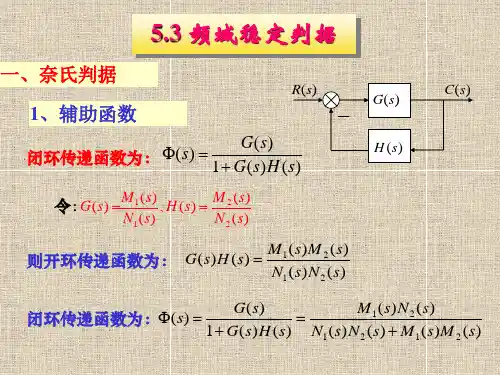




第五章频率域方法频率稳定判据(1)频率稳定判据两种频率稳定判据:奈奎斯特(Nyquist)稳定判据和对数频率稳定判据。
奈奎斯特判据是利用系统的开环幅相特性曲线判断闭环系统稳定性的一种方法,而对数频率稳定判据是利用系统的开环对数频率特性判断闭环系统的稳定性,两种方法本质上没有区别。
频率稳定判据是建立在幅角原理的基础上的,因此,下面先介绍有关幅角原理的内容。
设F(s)是复变量s 的单值函数,例如1212()()()=()()()()s z s z F s F s F s s p s p −−=∠−−1z 2z 1p 2p 0sjs 平面SΓ0F)(s F ∠jFΓF 平面设是s 平面上的一条封闭的轨线,且不经过F(s)的任何一个零点或极点。
对于上的任意一点,通过F(s)的映射,可以在F 平面上确定一个对应的点,称为的象,若沿顺时针移动一周,则对应的象在F 平面上形成一条封闭曲线。
S ΓF ΓS ΓS Γs F s s 12,z z 零点:12,p p 极点:1z 2z 1p 2p 0sjs 平面SΓ幅角原理若s 平面上的包围了F(s)的Z 个零点和P 个极点,则当点沿顺时针移动一周时,在F 平面上闭合曲线逆时针绕原点的圈数R 为P 和Z 之差,即R=P-Z若R<0,则表示顺时针方向绕原点的圈数。
S ΓS ΓF Γs 0F)(s F ∠jFΓF 平面12,z z 零点:12,p p 极点:(注意不能经过F(s)的任何一个零点和极点)S Γ)(s G )(s H 闭环121212()()()()=1()()()()()()M s N s G s s G s H s N s N s M s M s Φ=++11()()()M s G s N s =前向22()()()M s H s N s =反向开环1212()()()()()()M s M s G s H s N s N s =辅助函数121212()()()()()=1+()()()()N s N s M s M s F s G s H s N s N s +=辅助函数1122(),(),(),()M s N s M s N s 均为s 的实系数多项式开环特征多项式闭环特征多项式=)(s F F(s)的极点是开环的极点,F(s)的零点是闭环的极点。