当前位置：文档之家 › 自动控制原理第13讲(奈氏稳定判据)

自动控制原理第13讲(奈氏稳定判据)

  • 格式：ppt
  • 大小：1.68 MB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

奈氏判据教案(lx教案)

奈氏判据教案(lx教案)

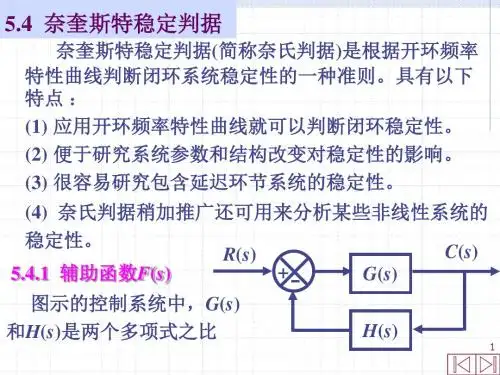
N1 ( s ) N 2 ( s ) M 1 ( s ) M 2 ( s ) F ( s) 1 G( s) H ( s) N1 ( s ) N 2 ( s )
考虑到物理系统中 , 开环传递函数分子的最高次幂必小于 分母的最高次幂N(S)大于M(S) ,
G( s) H ( s) M1 ( s) M 2 ( s) N1 ( s ) N 2 ( s )
2

2
0 0

若开环传递函数G(s)H(s)包含虚轴上的极点 ,
虚轴稍作变动 , 使其不过此极点 . 例如G(s)H(s)
包含积分环节时 , 习惯上以半径 趋于零的半 圆在原点右侧绕过这一极点 。 虚轴作这样的改变后，小半圆通过G(s)H(s)映 射到G(s)H(s)平面的象是半径趋于无穷的半圆。
0 0
n n : ( ) : 0 v

2


2
开环系统在虚轴上有极点情况 这时应将奈氏路径做相应的改变。如下图： 以极点为圆心，做半径为无穷小的右半圆， 使奈氏路径不通过虚轴上极点。


0 0
虚轴作这样的改变后，小半圆通过G(s)H(s)映射 到G(s)H(s)平面的象是半径趋于无穷的半圆。
由于 F (s) 1 G(s)H (s) 相差常数项1,所以 F(S) 包围原点的圈数也既是G(S)H(S)包围 (-1,j0)的圈数.
假设：S右半平面有P个开环极点， S右半平面有Z个闭环极点：

1G( j)H ( j)
:0

( j zi ) ( j pi )
相角由0变化到 v 2
开环系统在虚轴上有极点情况 这时应将奈氏路径做相应的改变。如下图： 以极点为圆心，做半径为无穷小的右半圆， 使奈氏路径不通过虚轴上极点。

自动控制原理奈氏判据共28页文档

自动控制原理奈氏判据共28页文档

Байду номын сангаас
谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人，越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智，自知者明。胜人者有力，自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
1、不要轻言放弃，否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人，常是愿意 去做，并愿意去冒险的人。“稳妥”之船，从未能从岸边走远。-戴尔．卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡，喝起来是苦涩的，回味起来却有 久久不会退去的余香。
自动控制原理奈氏判据 4、守业的最好办法就是不断的发展。 5、当爱不能完美，我宁愿选择无悔，不管来生多么美丽，我不愿失 去今生对你的记忆，我不求天长地久的美景，我只要生生世世的轮 回里有你。

(第13讲) 第五章 乃魁斯特(Nyquist)稳定性判据

(第13讲) 第五章 乃魁斯特(Nyquist)稳定性判据

在控制系统应用中，由
F (s) 1 G (s)H (s)
很容易确定
的P数。因此，如果， F (s )
的轨迹图中确定了R，则s平面上封闭曲线内的零点数
很容易确定。
开环传递函数与闭环传递函数的关系：
06-7-20
控制系统系统的稳定性分析
14
R(s)
C(s) G (s )
G (s)
B1 ( s ) A1 ( s )
06-7-20
控制系统系统的稳定性分析
3
奈奎斯特稳定判据(Nyquist Stability Criterion) 闭环传递函数
C (s) R (s) G (s)
R(s) G (s )
C(s)
H(s )
1 H ( s )G ( s )
图5-4-1 闭环系统 结构图
1 H ( s )G ( s ) 0
例如：考虑下列开环传递函数：
06-7-20 控制系统系统的稳定性分析 6
G (s)H (s)
6 ( s 1)( s 2 )
其特征方程为：
6
F (s) 1 G (s)H (s) 1
( s 1)( s 2 )

( s 1 . 5 j 2 . 4 )( s 1 . 5 j 2 . 4 ) ( s 1)( s 2 )
控制系统系统的稳定性分析 11
如果在s平面上曲线包围k个零点和k个极点(k=0,1,2…)，
即包围的零点数与极点数相同，则在 F ( s ) 平面上，
相应的封闭曲线不包围
F (s)
平面上的原点。
上述讨论是映射定理的图解说明，奈奎斯特稳 定判据正是建立在映射定理的基础上。

自动控制原理第13讲(奈氏稳定判据)

自动控制原理第13讲(奈氏稳定判据)
精选.
奈氏曲线图
10
Im
0 -1 0
(c)由于ν＝2，从 0 点逆时针
＝0 补画半径为无穷大的半园。
Re
P=0, N=-1
Z=2
该闭环不系统稳定。
0
Im
K Gc(S)S2(TS1)
Gd
(S)
10 S(TS1)
(d)ν=1,从 0 点逆时针
？
补画半径为无穷大的1/4园。
0
＝0
Z P R P 2N
GH( j )
K*
K 180
(s p1 )(s p2 )(s p3 ) 0 270
R: s 绕奈氏路径一周时，F(j)包围[F]平面(0, j0)点的圈数
N: 开环幅相曲线精G选.H(j)包围[G]平面(-1, j0)点的圈数
5
N的确定方法
开环幅相曲线包围(-1,j0)点的圈数，仅仅与幅相曲线
C
B
-1 A
0
Re
c
10 20 40
c
lg
100 200 400 01000
rad s
ZP2N
NN N
-90
-180
c
b
-270
精选.
a
lg rad
s
12
P205 5.12 Ti 0,K0, 判断闭环系统是否
题 开环 号 极点
穿越负实轴次数
奈氏判据 闭环极点
闭环 系统
(1) P=0 (2) P=0 (3) P=0 (4) P=0 (5) P=0 (6) P=0 (7) P=0 (8) P=1 (9) P=1 (10) P=1
精选.
8
(2)开环传递函数含ν 个积分环节 ν型系统

奈氏稳定判据课件

奈氏稳定判据课件
0
F
F (s)平面
8
1 、 奈氏判据数学基础…
j
z1
s
p1
0
z2
p2
s平面
s F(s) 映射
j F(s)
F(s)
0
F
F (s)平面
幅角原理: R=P-Z Z — s平面闭合曲线Γ包围F(s)的零点个数 P — s平面闭合曲线Γ包围F(s)的极点个数 R — 当s沿Γ顺时针运动一周，F(s)平面上闭合曲线гF 逆时针包围原点的圈数。
G( j0 )H( j0 )
14
1 、 奈氏判据数学基础…
3)G(S)H(S)含等幅振荡环节:
G(s)H (s)
(s2
1
2 n
)1
G1 ( s)
G(s)H (s) s jn e j
1
(2 jne j 2e2 j )1
G1( jn
e j )
j
jn
e j
e j( 90o )v1
(2n )v1
G1(
z1 )( s p1 )( s
z2 ) p2 )
F (s) s z1 s z2 s p1 s p2
F (s) s z1 s z2 s p1 s p2
2 0 (2 ) (2 ) 2
j
j
F(s)
z1
s
p1
0
z2
p2
s平面
s F(s) 映射
F(s)
重点回顾
幅相曲线绘制三要素
（1）开环幅相曲线的起点（ 0）和终点( )
（2）开环幅相曲线与实轴的交点
交点处的频率 x -------穿越频率
x : Im[G( jx )H ( jx )] 0 或 (x ) G( jx )H ( jx ) k , k 0,1,2 交点处坐标 Re[G( jx )H ( jx )]

奈奎斯特稳定判据

奈奎斯特稳定判据

s jw
w 0
F(s)平面上的映射是这样得到的：
① 以 s = jw 代入F(s)，令w 从0→∞变化，得第一部分的映射；
② 以 s=R·ej 代入F(s)，令R→∞， :
，得第二部分的映射；
22
③ 以 s = jw 代入F(s)，令w从－∞→0 ，得第三部分的映射。
得到映射曲线后，就可由柯西辐角定理计算 N = Z－P，式中Z、P是F(s)在s右 半平面的零点数和极点数。
令： G(s) M1(s) , H (s) M 2 (s)
N1 ( s)
N2 (s)
R(s)
C(Hale Waihona Puke )G(s)H (s)
则开环传递函数为：
闭环传递函数为：
16
Gk
(s)
M1(s)M 2 (s) N1(s)N2 (s)
(s) M1N2 M1M 2 N1N2
…………… (a) …………… (b)
将闭环特征式与开环特征式之比构成一个复变函数，得：
j 1
j 1
向量的幅值为
m
K s1 zi
F(s1)
i 1 n
s1 p j
5 j1
向量的相角为
m
n
F(s1) (s1 zi ) (s1 p j )
i1
j1
Im S平面
•
Re
6
Im
•
F(s)
(s)
F(s)平面 Re
当S平面上动点s从s1经过某曲线CS到达s2，映射到F(s)平面上也将是一段曲线CF ，该 曲线完全由F(s)表达式和s平面上的曲线CS决定。若只考虑动点s从s1到达s2相角的变 化量，则有
22
[奈奎斯特稳定判据]：若系统的开环传递函数在右半平面上有P个极点，且开环频率

自动控制原理-5.4奈氏判据


稳定性。
5.4.1 辅助函数F(s)
R(s)
+﹣
图示的控制系统中，G(s)
C(s) G(s)
和H(s)是两个多项式之比
H(s)
1
G(s) M1(s)
N 开环传递函数为：
1
(
s)
H(s) M2(s) N2(s)
Gk (s) G(s)H(s) 闭环传递函数为：

M1(s)M2(s) N1(s)N2(s)
（1）0型系统(开环没有串联积分 0 环节的系统)
s为包s围平虚面轴s 和整个右映半射平面。F(s)
正虚轴 j (:0)
F(j) ( : 0)
s
负虚轴 j (: 0)
F(j) ( : 0)
半径的半圆
( 1, j0)点
5
F(j)和G(j)H(j)只相差常数1。 F(j)包围原点就 是G(j)H(j)包围(-1，j0)点。
R=2 z = p R = 2
kT1T2
T1 T2
1
∴ 闭环系统是不稳定的 。
当 kT1T2 > 1 T1 T2
R=0
z = p R= 0
=0+
∴ 闭环系统是稳定的 。
Im

0
Re
增补线
16
(3) 由奈氏判据判稳的实际方法
用奈氏判据判断系统稳定性时，一般只须绘制从
j 1
F(s)曲线从B点开始，绕原点顺时针方向转了一圈。 4
幅角原理：如果封闭曲线内有Z个F(s)的零点， P个F(s)
的极点 ，则s 沿封闭曲线s 顺时针方向转一圈时，在F(s)
平面上，曲线F(s)绕其原点逆时针转过的圈数R为P和Z之

控制系统的奈氏图分析——自动控制原理


若N为正，则表示闭曲线C‘逆时针包围原点
的周数。
若N为负，则表示闭曲线C‘顺时针包围原点
的周数。
若N为零，则表示闭曲线C‘不包围原点Fs的零
点数
P——s平面上被封闭曲线C包围的Fs的极
点数
N ——F平面中封闭曲线C’包围原点的次数
j
C
s
(s+ZiII)
b）线的映射
2）映射定理 奈氏判据的理论基础是复变函数的映射定理。 定理：设F（S）：复变量S的单值解析函数， S平面 F（S）平面，它在S平面某一闭曲线C的内部共有P个极点和Z个零点，且 闭曲线C不通过F（S）的任一极点和零点。当S顺时针方向沿闭曲线变化一周时， 函数F（S）所取值一随之连续变化而在F平面上描出一个闭曲线C‘，曲线C‘称为C 的映射。 在上述情形下闭曲线C‘包围原点的周数N为
若增补奈氏曲线D
，当:逆时针包围, j0点的次数N等于
位于右半平面上开环极点数P。则闭环系统稳定，否则闭环系统不稳定。
增补奈氏轨迹映射出的奈氏轨迹分析*：
可见增补奈氏轨迹映射为半径的圆曲线变点相角变化从M90 M90 如 M=1， -M：90090
M=2时， -M：180 0 180
一型系统的奈氏曲线
二型系统的奈氏曲线
（-M：900 -90）
（-M：1800 -180）
=0-
=
=0+
=
=0+
GH平面
=0GH平面
例：设开环传函数
试用奈氏判据判定系统稳定性 解：作奈氏曲线考虑增补 当:顺时针 包围,j0点2次， N=2 P=0 Z=2 不稳定
=0-
= •
(-1,j0)
=0+

自动控制原理Nyquist稳定判据

(N = m － n , 若N≥ 1，n不会为负值，则必有m ≥1)
3.4，Nyquist稳定判据
例3.15已知开环传递函数 判断系统稳定性
G0 (
j
)
( T1
j
k 1 )( T2
j
1)
Nyquist图画法(示意图)
Im
G0( j ) G0( j )G0( j )
0 180 0
j
(1)特殊点
面上的Nyuist图顺时针包围原点N次。 n>m时
多数情况，当s从0 ± j∞ 时, G0(s) 0, F(s) = 1+G0(s) 0
3.4，Nyquist稳定判据
N=m― n
DC(s)=0的根 闭环极点
D0(s)的根 开环极点
(3)开环频率特性G0(jω )和Nyuist图
开环传递函数G0(s)，令s = jω ，即开环频率特性G0(jω )
3.4，Nyquist稳定判据
利用柯西复角原理判稳定的思路：
(1)使F(s)与系统传递函数相联系 (2)封闭曲线域为右半平面（或左半平面） (3)使封闭曲线为虚轴，与频率特性相联系
3.4，Nyquist稳定判据
2，D形围线和Nyquist图：
+
G(s)
-
H(s)
开环传递函数
G0( s ) G( s )H ( s )
例3.17 G0 (
j )( T1j来自1)( T2k( T01 j 1 )( T01 j 1 ) j 1)( T3 j 1)( T4 j 1)( T5
j 1)
T1 ,T2 ,T3 T01 ,T02 T4 ,T5
Im
-1
k Re
0
Nyquist判据： N=0，n=0，所以m=0 系统稳定

奈氏判据


P 2

S2
Z2

P 1
0

0
F (S1 )ຫໍສະໝຸດ ReS3Ls
(a )
(b)
LF
图4-36
S 和 F(s) 的映射关系
8
设 F (s) 在S平面上，除有限个奇点外，为单值的连续函 数，若在S平面上任选一封闭曲线 Ls ，并使 Ls不通过 F (s) 的奇点，则S平面上的封闭曲线 Ls映射到F(s)平面 上也是一条封闭曲线 LF 。当解析点s按顺时针方向沿 Ls 变化一周时，则在 F (s) 平面上，LF 曲线按逆时针方 向旋转的周数N（每旋转2弧度为一周），或 LF 按逆 时针方向包围 F(s)平面原点的次数，等于封闭曲线 Ls 内包含F(s)的极点数P与零点数Z之差。即
Im
GH
0 0
Im
1 0
GH
0
Im
GH

0 0
1
0
Re
Re 0
1
0
Re
T
(b)
T
(c )
T
稳定
图4-42 系统的奈氏曲线
1
0

(1)
F ( j)
LGH
G( j ) H ( j )

Ls
LF
（a）s平面的Nyquist轨迹 （b）［F］平面的奈氏曲线 （c）［GH］平面的奈氏曲线
图4-37
12
奈氏轨迹 Ls在GH平面上的映射LGH称为奈奎斯特曲线或奈氏曲线.
三、奈奎斯特稳定判据 闭环系统稳定的充分必要条件是，GH 平面上的奈奎斯
第四节
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

lg
c
b
a
rads
12
-270
P205 5.12 Ti 0, K 0 , 题 开环 号 极点 (1) P=0 (2) P=0 穿越负实轴次数
判断闭环系统是否稳定
奈氏判据 闭环 闭环极点 系统 Z=P-2N=2 不稳定 Z=P-2N=0 稳定
NN 1 1 N 0
所以，闭环系统稳定。
0

Re
K (TS 1) Gb ( S ) S2

奈氏曲线图
10
0 点逆时针 (c)由于ν＝2，从
0

Im -1 0
＝0
Re
补画半径为无穷大的半园。 P=0, N=-1 Z=2 该闭环不系统稳定。 K 10 Gc ( S ) 2 G ( S ) d S (TS 1) S (TS 1) (d)ν=1,从 0 点逆时针
§5.3 频域稳定判据
§5.3
频域稳定判据
§5.3 频域稳定判据
系统稳定的充要条件 — 全部闭环极点均具有负的实部 代数稳定判据 — Ruoth判据 由闭环特征多项式系数（不解根）判定系统稳定性 不能用于研究如何调整系统结构参数来改善系统稳定性及 性能的问题 频域稳定判据 —
Nyquist 判据 对数稳定判据

0

Im
？
＝0

0
Re
补画半径为无穷大的1/4园。 虚线的终端落在负实轴上 P=1, N=-1/2， Z=1-2(-1/2)=2
11
奈氏曲线图 非最小相位系统
N N N 该闭环系统不稳定。
3 在对数坐标图上应用奈奎斯特稳定性判据
L( ) 20 lg GH
40
G( j ) H ( j ) 1
个数相同
§5.3.1
奈奎斯特稳定判据
2 2 0
(3)
设F(s)在右半s平面有
Z个零点 (闭环极点) Z=2 P个极点 (开环极点) P=1
( s 1 )( s 2 )( s 3 ) F ( j ) ( s p1 )( s p2 )( s p3 ) 2 0 0
13
注意问题
1. 当[s]平面虚轴上有开环极点时，奈氏路径要从其右边
绕出半径为无穷小的圆弧；[G]平面对应要补充大圆弧
2. N 的最小单位为二分之一
0
3.
闭环系统不稳定 闭环系统稳定 有误！
Z
0
0
N 2
N 2
N N N 2 2 0
幅相曲线在负实轴(-.-1) 区间的正负穿越如图所示
- + - + -1 0
Re
6
稳定性分析举例 (1)开环传递函数不含积分环节（0型系统） 直接采用Z=P-2N的稳定性判据 例1 给出三个开环传递函数不含有积分环节的 奈氏曲线，试判断系统的稳定性。 K Im Ga (S ) (T1S 1)(T2 S 1)
( s )
D( s ) ( s 1 )( s 2 )( s 3 ) N ( s ) ( s p1 )( s p2 )( s p3 )
G( s ) 1 GH ( s )
F(s)的特点
零点 i : 闭环极点 ① F(s)的 极点 pi : 开环极点 ② F ( j ) 1 GH ( j )
Im

0
0
Re
所以，闭环系统稳定。
K Ga ( S ) S (TS 1)
0

奈氏曲线图
9
例2 给出含有两个积分环节的开环系统
幅相曲线，试判断系统的稳定性。
(b)由于ν＝2，从 0点逆时针 补画半径为无穷大的半园。 P=0, N=0 Z=0
Im -1

0
0
பைடு நூலகம்
0
P=0,
N=0
-1
0 K Re
Z=P-2N=0 该闭环系统稳定。

（a）P＝0 奈氏曲线
7
Im
0
(b) G (S) b
0
K (T1S 1)(T2S 1)(T3S 1)
-1
K Re
P=0,
NN 1 1 N 0

Im
Z=P-2N=2 闭环系统不稳定。
Im
dB
C B
G( j ) H ( j ) 1

-1
c
A
0
Re
20
c
0.1 0.4 1 2 4 10 20 40 100 200 400 0 1000
lg
0 -20
rad s
-40
Z P 2N
N N N
j ( )0
0 -90 -180
K* K * M ( s) GH ( s ) ( s p1 )( s p2 )( s p3 ) N ( s) G( s ) ( s ) 1 GH ( s )
§5.3.1
奈奎斯特稳定判据
(2)
构造辅助函数 F(s) F ( s ) 1 GH ( s )
K * M ( s) N ( s) K * M ( s) 1 N ( s) N ( s) ( s p1 )( s p2 )( s p3 ) K * M ( s ) ( s p1 )( s p2 )( s p3 )
s 绕奈氏路径转过一周， F(j)绕[F]平面原点转过的角度jF()为
F ( j ) 2 ( Z P ) 2 ( P Z ) 2R
Z P R P 2N
K* GH ( j ) ( s p1 )( s p2 )( s p3 )
K 180 0 270
0
0 K -1

Re
K (c) Gc (S) (TS 1)
1 1 N N N 0 P=1, 2 2

奈氏曲线图
Z=P-2N=0 闭环系统稳定。
8
(2)开环传递函数含ν 个积分环节
ν型系统
绘制开环幅相曲线后，应从频率0+对应的点 开始，逆时针补画ν/4个半径无穷大的圆。 －900ν 例2 给出含有1个积分环节的开环系统幅相曲线， 试判断系统的稳定性。 (a)ν=1,从 0 点逆时针 补画半径为无穷大的1/4园。 -1 P=0, N=0 Z=0
NN 00 N 0 1 1 Z=P-2N=2 不稳定 (3) P=0 NN N 0 00 Z=P-2N=0 稳定 (4) P=0 NN N 0 (5) P=0 NN 1 1 Z=P-2N=2 不稳定 N 0 (6) P=0 NN 110 Z=P-2N=0 稳定 N 1 10 Z=P-2N=0 稳定 (7) P=0 NN N 1 1 N 0 (8) P=1 NN 稳定 2 2 Z=P-2N=0 00 Z=P-2N=1 不稳定 (9) P=1 NN N 0 1 1 N N N 0 2 2 (10) P=1 Z=P-2N=2 不稳定
R: s 绕奈氏路径一周时，F(j)包围[F]平面(0, j0)点的圈数 N: 开环幅相曲线GH(j)包围[G]平面(-1, j0)点的圈数
N的确定方法
开环幅相曲线包围(-1,j0)点的圈数，仅仅与幅相曲线 穿越实轴区间(-,-1)的次数有关。 把自上向下(逆时针)穿越这个区间的次数表示为 N 把自下向上(顺时针)穿越这个区间的次数表示为 N Im 注意：若穿越时从这个区间的实轴上开始时 记为半次正(半次负)穿越。 右图中
由开环频率特性直接判定闭环系统的稳定性 可研究如何调整系统结构参数改善系统稳定性及性能问题
§5.3.1
奈奎斯特稳定判据
奈奎斯特稳定判据
K ( T1 s 1) ( T2 s 1 )( T3 s 1 )
(1)
§5.3.1
解释 设
Z P 2N
G( s)
说明
设
K1 Z P 2 N 1 2 0 1 不稳定 K 1 K 2 Z P 2 N 1 2 ( ) 2 不稳定 2 系统结构图如图所示