5.3用频域分析法分析系统的稳定性解析

控制系统的稳定性分析简介控制系统的稳定性是指系统在受到干扰时，能够保持从初始状态返回到稳定的平衡状态的能力。

稳定性是控制系统设计和分析的重要指标之一，对于确保系统正常运行具有重要意义。

在本文档中，我们将探讨控制系统的稳定性分析方法。

稳定性概念在控制系统中，稳定性可以分为两种类型：绝对稳定和相对稳定。

1.绝对稳定：当系统在受到干扰后能够恢复到初始的平衡状态并保持在该状态时，我们称系统是绝对稳定的。

2.相对稳定：当系统在受到干扰后能够恢复到新的平衡状态并保持在该状态时，我们称系统是相对稳定的。

稳定性分析方法为了评估控制系统的稳定性，我们通常使用以下几种分析方法：1. 传递函数分析传递函数分析是一种常用的稳定性分析方法，它通过将控制系统转化为传递函数的形式，进行频域和时域的分析。

在频域分析中，我们可以使用频率响应函数（Bode图）来评估系统的稳定性。

Bode图由幅度曲线和相位曲线组成，通过分析这两个曲线可以判断系统是否稳定。

在时域分析中，我们可以使用单位斯蒂文斯响应函数来评估系统的稳定性。

单位斯蒂文斯响应函数是指控制系统对于单位阶跃输入的响应。

2. 决策稳定性分析决策稳定性分析方法是一种直观的稳定性评估方法，它通过观察控制系统的反馈回路来判断系统的稳定性。

如果控制系统的反馈回路中存在零点或极点位于右半平面，则系统将是不稳定的。

另外，如果控制系统的相位裕度和增益裕度分别小于零和一，则系统也将是不稳定的。

3. 根轨迹分析根轨迹分析是一种图形化的稳定性分析方法，它通过绘制系统传递函数的根轨迹来评估系统的稳定性。

根轨迹是表示系统极点随控制参数变化的轨迹图，它可以直观地显示系统的稳定性和响应特性。

如果根轨迹上的所有极点都位于左半平面，则系统是稳定的。

4. Nyquist稳定性判据Nyquist稳定性判据是一种基于频域分析的稳定性判据，它利用开放式系统的频率响应来评估系统的稳定性。

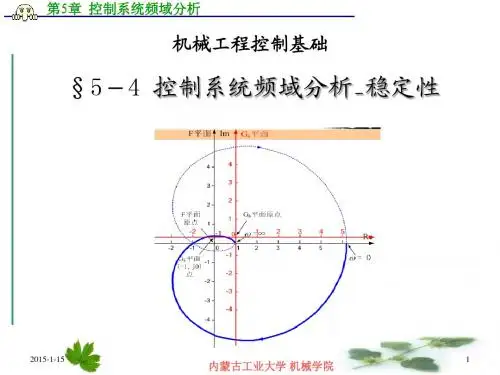
Nyquist稳定性判据通过绘制控制系统的开环频率响应曲线，并计算曲线绕原点的圈数来判断系统是否稳定。

自动控制系统的稳定性分析自动控制系统在现代工程中起着至关重要的作用。

稳定性是评价自动控制系统性能的一个重要指标，系统稳定性的分析对于系统设计、调试和优化至关重要。

本文将对自动控制系统的稳定性进行分析，并探讨常用的稳定性分析方法。

1. 引言自动控制系统的稳定性是指在外部扰动或参数变化的情况下，系统能够保持稳定的能力。

稳定性分析是评价系统的关键特性之一，它决定了系统的可靠性和性能。

稳定性分析的目的是通过研究系统的传递函数或状态方程，确定系统的稳定性边界并评估系统的稳定性。

2. 稳定性的判据用于判断自动控制系统稳定性的最常见方法是分析系统的极点位置。

极点是系统传递函数或状态方程的特征根，它们的位置决定了系统的稳定性。

常见的判据有：- 实部均小于零：当系统的所有极点的实部都小于零时，系统是稳定的。

- 实部均小于等于零：当系统的所有极点的实部都小于等于零时，系统是边界稳定的。

- 实部均小于一：当系统的所有极点的实部都小于一时，系统是渐进稳定的。

- Nyquist稳定判据：通过绘制系统开环传递函数的Nyquist曲线，判断曲线与负实轴的交点个数来确定系统的稳定性。

3. 稳定性分析方法3.1 根轨迹法根轨迹法是一种图形化分析方法，通过绘制系统极点随参数变化的轨迹，可以直观地了解系统的稳定性边界。

根轨迹图能够反映了系统参数变化时的稳定性情况，并通过分析轨迹与虚轴的交点个数来判断系统的稳定性。

3.2 频率响应法频率响应法是一种以频域为基础的稳定性分析方法，它通过研究系统在不同频率下的响应特性来判断系统的稳定性。

常用的频率响应法包括振荡器法、相频曲线法和伯德图等。

这些方法通过测量输入输出之间的幅度和相位差来评估系统的稳定性。

3.3 状态空间法状态空间法是一种基于系统的状态方程进行稳定性分析的方法。

通过将系统的状态方程转化为特征方程，可以分析特征根的位置来判断系统的稳定性。

状态空间法具有较强的灵活性，可以应用于复杂的多变量系统。

控制系统稳定性分析在控制系统的设计和应用中，稳定性是一个至关重要的指标。

控制系统的稳定性分析能够帮助工程师确定系统是否能够在各种工况下保持平稳运行，并避免产生不稳定或振荡的现象。

本文将介绍控制系统稳定性分析的基本概念和方法。

一、稳定性概述稳定性是指在系统受到扰动或干扰的情况下，系统能够在一定的范围内保持平衡或恢复到平衡状态的能力。

对于控制系统来说，稳定性是一个必要条件，只有具备了稳定性，系统才能够实现准确、可靠的控制任务。

二、时域稳定性分析方法时域稳定性分析方法主要通过观察系统的响应和特征方程的性质来判断系统的稳定性。

其中，常用的方法包括：1. 判据法：通过判断系统的极点位置来确定稳定性。

当系统所有极点的实部都小于零时，系统是稳定的。

2. 力学振荡器法：将系统等效为一个力学振荡器进行分析，通过计算振荡器的振荡周期和阻尼比等参数来判断系统的稳定性。

3. Lyapunov稳定性分析法：利用离散或连续的Lyapunov函数来刻画系统的稳定性，通过判断Lyapunov函数的增减性来确定系统是否稳定。

三、频域稳定性分析方法频域稳定性分析方法通过对系统传递函数进行频谱分析，利用频率响应特性来判断系统的稳定性。

常用的频域稳定分析方法包括：1. Bode图法：将系统的传递函数表示为极形式，并将其转化为幅频特性和相频特性的曲线来分析系统的稳定性。

2. Nyquist图法：通过将系统的开环传递函数在复平面上绘制出极坐标图，根据图形上的奇点个数来判断系统的稳定性。

3. Nichols图法：将系统的开环传递函数在奈氏图上绘制出闭环频率响应曲线，通过曲线的形状和位置来判断系统的稳定性。

四、数值稳定性分析方法数值稳定性分析方法是利用计算机仿真和数值模拟的手段来分析系统的稳定性。

通过将系统的差分方程或微分方程转化为数值算法，然后利用数值方法求解方程，观察系统的响应和稳定性指标来分析系统的稳定性。

五、稳定性分析的实际应用控制系统的稳定性分析在实际工程中具有重要的应用价值。

自动控制原理稳定性分析知识点总结自动控制原理是现代控制理论中的基础学科，稳定性分析是其中重要的一部分。

稳定性分析主要研究控制系统中信号的稳定性，即系统输出响应是否会收敛或发散。

本文将对自动控制原理稳定性分析的知识点进行总结。

1. 稳定性的概念稳定性是描述控制系统中输入与输出之间关系的一个重要性质。

一个稳定的控制系统能够在一定范围内抑制干扰和噪声，保持输出信号在一定精度范围内的波动。

稳定性可以分为绝对稳定和相对稳定两种情况。

2. 稳定性分析方法稳定性分析方法主要包括代数稳定性判据、频域稳定性判据和时域稳定性判据三种。

2.1 代数稳定性判据代数稳定性判据通过分析系统的特征值或者判别函数来判断系统的稳定性。

其中，常用的代数稳定性判据有判别函数法、判别方程法和位置根判据法等。

2.2 频域稳定性判据频域稳定性判据是通过绘制系统的频率响应曲线来分析系统的稳定性。

常见的频域稳定性判据包括Nyquist稳定性判据和Bode稳定性判据等。

2.3 时域稳定性判据时域稳定性判据是通过分析系统的状态方程或传递函数的时域响应曲线来判断系统的稳定性。

常见的时域稳定性判据有极点位置法、根轨迹法和奈奎斯特判据等。

3. 稳定性的分类根据系统特征值的位置，稳定性可以分为绝对稳定、相对稳定和不稳定三种情况。

3.1 绝对稳定当系统的所有特征值都位于负半平面时，系统被称为绝对稳定。

绝对稳定的系统具有良好的稳定性，能够有效地抑制干扰和噪声。

3.2 相对稳定当系统的部分特征值位于负半平面，而部分特征值位于零轴或者正半平面上时，系统被称为相对稳定。

相对稳定的系统在一定的条件下可以保持输出的稳定性。

3.3 不稳定当系统的特征值中存在正实部或者纯虚部的特征值时，系统被称为不稳定。

不稳定的系统输出会发散或者产生不稳定的振荡。

4. 稳定性分析的应用范围稳定性分析在控制系统设计和优化中起到了重要的作用。

通过稳定性分析，可以评估系统的抗干扰能力和控制性能，为系统设计提供理论依据。

控制系统的稳定性分析与评估控制系统是现代工程中的重要组成部分，其稳定性对于系统的正常运行至关重要。

在控制系统设计和维护中，稳定性的分析与评估是必不可少的步骤。

本文将介绍控制系统稳定性分析的方法和评估的指标，并探讨其在工程实践中的应用。

一、稳定性分析方法稳定性分析是控制系统设计的基础，常用的稳定性分析方法有时域法、频域法和根轨迹法。

时域法是基于控制系统的时间响应进行分析。

通过计算系统的单位阶跃响应或脉冲响应，可以获取系统的稳定情况。

时域法能够提供系统的稳定性指标，如超调量、峰值时间和稳态误差等。

频域法是基于控制系统在频域上的特性进行分析。

通过对系统的频率响应进行采样和分析，可以得到幅频特性和相频特性。

频域法能够提供系统的增益裕度和相位裕度等指标，可以帮助判断系统的稳定性。

根轨迹法是基于控制系统传递函数的极点和零点分布进行分析。

通过绘制系统的根轨迹图，可以直观地观察系统的稳定性和响应特性。

根轨迹法可以帮助系统设计者调整参数，以达到所需的稳定性要求。

这些稳定性分析方法可以相互结合使用，以提供更全面、准确的稳定性评估结果。

二、稳定性评估指标稳定性评估是根据稳定性分析的结果，对控制系统的稳定性程度进行评估的过程。

常用的稳定性评估指标有阻尼比、杆塞尔稳定判据和奈奎斯特稳定判据等。

阻尼比是评估系统阻尼效果的指标，用于描述系统的衰减程度。

阻尼比为1时系统为临界稳定，大于1则系统为超阻尼，小于1则系统为欠阻尼。

杆塞尔稳定判据是基于系统极点的位置判断系统的稳定性。

系统所有极点的实部均小于零时，系统是稳定的。

杆塞尔稳定判据适用于分析线性时不变系统的稳定性。

奈奎斯特稳定判据是使用频域法进行稳定性评估时的重要指标。

奈奎斯特稳定判据通过绘制控制系统的奈奎斯特曲线，判断系统的稳定性。

奈奎斯特稳定判据可应用于分析非线性、时变以及传感器和执行器等带非线性特性的控制系统。

三、工程应用稳定性分析与评估在工程实践中具有重要的应用价值。

控制系统中的稳定性分析方法稳定性是控制系统设计和分析中至关重要的概念，它决定了系统的响应是否会随时间或外部干扰的变化而发散或者衰减。

稳定性分析是评估系统的稳定性并识别可能导致系统不稳定的因素的过程。

掌握稳定性分析方法对于设计和优化控制系统至关重要，本文将介绍几种常用的稳定性分析方法。

1. 时间域稳定性分析方法时间域稳定性分析方法是通过研究控制系统的时间响应来评估其稳定性。

其中，最常用的方法是研究系统的阶跃响应。

阶跃响应可以模拟当系统受到单位阶跃输入时的行为。

通过分析阶跃响应中的振荡和衰减情况，可以判断系统的稳定性。

常见的时间域稳定性分析方法包括：- 稳定性判据法：根据控制系统的特征方程的根在左半平面的个数确定系统的稳定性。

例如，系统的特征方程所有根的实部都小于零，则系统是稳定的。

- 跟踪法：通过分析阶跃响应的振荡情况，如超调量和调整时间，来评估系统的稳定性。

例如，当系统的超调量小于一定阈值并且调整时间满足要求时，可以认为系统是稳定的。

2. 频域稳定性分析方法频域稳定性分析方法是通过研究系统的频率响应来评估其稳定性。

频率响应可以揭示系统对不同频率信号的传递特性。

常用的频域稳定性分析方法包括：- Nyquist稳定性判据：根据系统的开环传输函数在复频域上的轨迹来判定系统的稳定性。

如果系统的开环传输函数的轨迹不绕复平面的-1点（-1+j0）（即Nyquist轨迹）或者经过-compensation的选择，可以判定系统是稳定的。

- 辐角判据：通过分析系统的相位频率特性曲线，判断系统的辐角是否满足稳定性条件。

如果系统的相位频率特性曲线满足一定的条件，例如相位频率特性曲线的最大幅值小于180度，则系统可以被认定为是稳定的。

3. Lyapunov稳定性分析方法Lyapunov稳定性分析方法是利用李雅普诺夫函数及其性质来评估系统的稳定性。

李雅普诺夫函数是一个具有良好性质的函数，可以确定系统状态的稳定性行为。

通过构建李雅普诺夫函数，并根据其形式和性质对系统进行分析，确定系统的稳定条件。

控制理论工程中频域分析与系统稳定性研究近年来，控制理论工程在工业自动化领域中发挥着越来越重要的作用。

频域分析与系统稳定性研究是其中的关键内容之一。

本文将介绍频域分析的基本概念，并探讨系统稳定性的研究方法与重要性。

频域分析是一种常用的工程控制方法，用于描述系统对不同频率信号的响应。

频域分析的核心是将时域信号转换成频域信号，通过分析频域特性来评估系统性能。

频域分析的基础工具为傅里叶变换，通过将信号分解成一系列不同频率的正弦和余弦函数，可以得到系统在不同频率下的幅频和相频特性。

在频域分析中，Bode图是最常用的工具之一。

Bode图由系统的幅频特性和相频特性组成，通过画出系统的频率响应曲线，我们可以直观地了解系统的增益和相位随频率的变化。

通过分析Bode图，我们可以判断系统的稳定性、带宽和相位裕度等重要性能指标。

在实际工程应用中，频域分析经常用于系统校准、控制回路设计和系统故障诊断等方面。

通过频域分析，我们可以确定系统的共振频率、稳态误差、相位余量等参数，从而更好地设计控制器和优化系统性能。

此外，频域分析还可以用于识别和解决系统中存在的不稳定性问题，从而确保系统的稳定运行。

系统稳定性是控制理论工程中至关重要的一个研究方向。

一个稳定的系统具有良好的动态响应特性，能够在外部扰动和参数变化的情况下保持稳定性。

稳定性的研究旨在设计控制策略并评估系统的性能。

稳定性研究中常用的方法包括极点分析和稳定裕度分析。

极点分析是通过分析系统的特征方程的根来判断系统的稳定性。

稳定裕度分析是通过计算系统的增益和相位裕度来评估系统的稳定性。

这些方法可以帮助我们预测系统的稳定性边界，从而指导控制器设计和系统调整。

系统稳定性研究对于工程实践具有重要的意义。

一个稳定的系统能够在复杂的环境下保持预期的性能，有效地控制工业过程，并提高系统的可靠性和安全性。

稳定性研究还可以帮助我们预测系统的动态行为、防止系统不稳定或振荡等问题的发生，从而减少设备损坏和安全事故的风险。

线性系统的时域与频域稳定性分析研究一、线性系统的定义及时域稳定性分析线性系统是指系统的输出与输入之间存在线性关系的系统，可以表示为y(t)=Ax(t)，其中A为系统的矩阵，x(t)为输入信号，y(t)为输出信号。

时域稳定性是指系统在时域的响应是否具有稳定性，即系统长时间内是否会趋于平衡状态。

对于线性系统而言，只需要分析系统的特征方程即可进行稳定性分析。

通过特征方程的根，判断系统的稳定性，具体的方法有如下两种：1. 系统稳定的充要条件是其特征方程的所有根都是复平面的左半部分，即实部小于零。

2. 如果特征方程的根中存在于虚轴上的根，那么对于系统的稳定性分析需要进行更为详细的分析。

二、线性系统的频域稳定性分析方法由于傅里叶变换的普遍性，线性系统的频域稳定性更加普遍。

频域稳定性是指系统对于所有输入信号都具有稳定性。

通常情况下，我们使用拉普拉斯变换来分析系统的频域稳定性。

对于系统输入信号X(s)，系统输出信号Y(s)，系统传递函数为H(s)，则系统的稳定性可以通过传递函数的零点和极点来分析。

通常情况下，稳定系统的传递函数H(s)的所有极点都在复平面的左半部分。

三、线性系统的稳定性分析实例为了更好地说明线性系统稳定性分析的具体方法，我们在此举一个实例来说明。

假设我们现在有一个系统，其传递函数为：H(s)=s+3 / s^2+5s+6我们需要分析该系统在时域和频域中的稳定性。

（1）时域稳定性分析由于该系统的特征方程为s^2+5s+6=0，其特征方程的根为-2,-3，均为负实数，因此该系统为时域稳定的。

（2）频域稳定性分析该系统传递函数的分母为(s+2)(s+3)，因此其极点分别为-2,-3。

由于这些极点均位于左半部分，因此该系统为频域稳定的。

四、结论线性系统的稳定性是系统分析和控制中的基础问题。

通过以上实例和方法的介绍，我们可以清晰地了解线性系统的时域与频域稳定性分析的基本步骤，这对于我们理解和掌握系统分析和控制具有重要的意义。