§3.3 纯剪切§3.4圆轴扭转时的应力

圆轴扭转时的应力与强度条件扭转是杆件的基本变形形式之一。

工程中有些杆件，因承受作用平面垂直于杆轴线的力偶作用，而发生扭转变形。

通常将这种杆件称为轴，如传动轴等。

本讲主要分析圆截面杆的扭转。

非圆截面杆受扭时，不能用材料力学的理论求解。

图1 圆轴的扭转扭转变形和受力特点：杆件受到大小相等、方向相反且作用平面垂直于杆件轴线的力偶作用，杆件的横截面绕轴线产生相对转动。

● 外力特征：力偶矩矢平行于杆的轴线。

力偶矩矢方向按右手螺旋法则确定。

● 力偶变形特点：各轴线仍为直线，杆件的任意两个横截面发生绕轴线的相对转动。

一、圆轴扭转的应力图2 圆轴扭转的剪应力分布图图2中，tW T=max τ （1） 式（1）中，t W 为抗扭截面模量，是仅与横截面尺寸有关的量。

实心圆轴163D W n π=，空心圆轴Dd D W n16)(44-=π。

二、扭转强度分析为了保证圆轴安全可靠地工作，应使轴内的最大剪应力不超过材料的许用剪应力[]τ，即A Bm axm τ][max ττ≤=tW T（9-7） 根据圆轴扭转的强度条件，可以进行强度校核、截面设计和确定许可载荷等三大类强度计算问题。

例：传动轴上有三个齿轮，齿轮2为主动轮，齿轮1和齿轮3输出扭矩分别为N.m 3.391=m 和N.m 1553=m 。

若轴的材料为45钢，[]a MP 40=τ。

根据强度确定轴的直径。

解: (1) 计算力偶距m 2 。

m N m m m .3.194312=+=（2）画扭矩图。

（3）根据强度条件计算直径。

从扭矩图上可以看出，齿轮2与3 间的扭矩绝对值最大。

][163maxmax max τπτ≤==DT W T t []m 0272.0104014.31551616363max=⨯⨯⨯=≥τπT D1231m 2m 3m 0.30.4mxT155N.m39.3N.m。

直升机的旋转轴
电机每秒输入功：外力偶作功完成：
×
=P W
M W
e
⋅
=
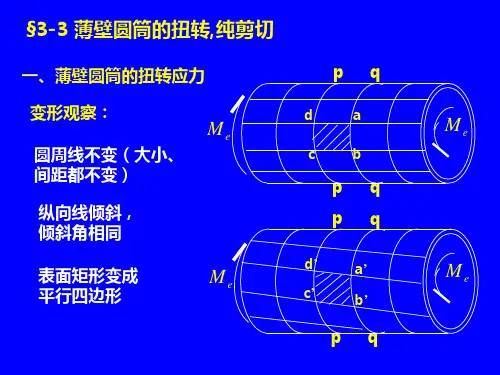
形状、大小、间距不变，各圆周线只是绕轴线转动了一个角度。

倾斜了同一个角度，小方格变成了平行四边形。

τdα
τ
l
ϕ
做薄壁圆筒的扭转试验可得
l
是材料的一个弹性常数，称为剪切弹性模量，G的量纲各向同性材料，三个弹性常数之间的关系：
ρργγtg ≈x
d d d ′=x d d ϕρ⋅=O 1O 2ABCD 为研究对象
D’
微段扭转变形d dx Rd dx DD tg ϕγγ==≈'d ϕ/ d x －扭转角沿x 轴的变化率
扭转变形计算式
O d A ρTρ⋅
（实心截面）
1、横截面上角点处，切应力为零；
2、横截面边缘各点处，切应力
3、切应力沿横截面周边形成与
4、横截面周边长边中点处，切应力最大。

有关，见教材P93 之表3.2。

圆轴扭转时的应力计算公式在我们学习力学的过程中，圆轴扭转时的应力计算公式可是个相当重要的家伙。

咱们今天就来好好唠唠它！先来说说啥是圆轴扭转。

想象一下，你手里拿着一根棍子，然后像拧麻花一样去转动它，这时候棍子内部就会产生应力。

圆轴扭转就是类似这样的情况啦。

那圆轴扭转时的应力计算公式到底是啥呢？它就是：τ = Tρ / Ip 。

这里的τ 表示的是扭转切应力，T 是扭矩，ρ 是所求应力的点到圆心的距离，Ip 则是极惯性矩。

咱们来仔细瞅瞅这个公式。

扭矩 T 就好比是你拧棍子的那个力气，力气越大，应力也就越大。

而ρ 呢，距离圆心越远，应力也就越大，就像离圆心远的地方更“吃力”。

极惯性矩 Ip 则反映了圆轴抵抗扭转的能力，它越大，应力就相对越小。

我记得之前在给学生们讲这个知识点的时候，有个小同学瞪着大眼睛问我：“老师，这公式咋来的呀？”我就给他举了个例子。

咱们把圆轴想象成是由好多好多层薄圆环组成的。

当圆轴扭转时，每一层薄圆环都会发生相对的滑动，就像是在互相“拉扯”。

通过对这种“拉扯”的分析和计算，咱们就得出了这个公式。

在实际应用中，这个公式可太有用了。

比如说在机械设计里，要设计一根传动轴，就得先算出它在工作时扭转产生的应力，看看是不是在材料能承受的范围内。

要是应力太大，轴就可能会断掉，那可就出大问题啦！再比如，在一些工程结构中，像桥梁的支撑柱，如果受到扭转力的作用，也得用这个公式来算算应力，保证结构的安全稳定。

咱们在解题的时候，一定要搞清楚每个参数的含义和单位，千万别马虎。

有一次考试，就有同学因为把单位搞错了，结果整个答案都错了，那叫一个可惜哟！总之，圆轴扭转时的应力计算公式虽然看起来有点复杂，但只要咱们认真理解，多做几道题练练手，就一定能掌握它，让它成为我们解决问题的有力工具。

怎么样，同学们，这回对圆轴扭转时的应力计算公式是不是更清楚啦？加油，相信大家都能学好这部分知识！。

圆轴纯扭转时横截面上的正应力研究圆轴纯扭转时横截面上的正应力研究圆轴纯扭转是一种常见的力学现象，它在工程领域中得到广泛应用。

在圆轴纯扭转时，横截面上的正应力是一个重要的研究对象。

本文将介绍圆轴纯扭转时横截面上的正应力的研究。

圆轴纯扭转的基本概念圆轴纯扭转是指在轴线方向施加一个扭矩，使得轴发生扭转变形的过程。

在圆轴纯扭转时，轴的横截面上会产生正应力和剪应力。

其中，正应力是指垂直于横截面的应力，剪应力是指平行于横截面的应力。

圆轴纯扭转时横截面上的正应力在圆轴纯扭转时，横截面上的正应力可以通过以下公式计算：σ = T*r/J其中，σ是横截面上的正应力，T是施加在轴上的扭矩，r是横截面上的半径，J是横截面的极惯性矩。

从上述公式可以看出，横截面上的正应力与扭矩成正比，与半径成反比，与极惯性矩成反比。

因此，在圆轴纯扭转时，如果扭矩增大，横截面上的正应力也会增大；如果半径增大，横截面上的正应力会减小；如果极惯性矩增大，横截面上的正应力也会减小。

圆轴纯扭转时横截面上的正应力分布在圆轴纯扭转时，横截面上的正应力分布是一个圆周分布。

具体来说，横截面上的正应力最大值出现在轴的中心，随着半径的增大逐渐减小，最终趋于零。

这种分布规律可以通过以下公式表示：σ = T*rmax/J * (1-r^2/rmax^2)其中，σ是横截面上的正应力，T是施加在轴上的扭矩，r是横截面上的半径，rmax是横截面的最大半径，J是横截面的极惯性矩。

从上述公式可以看出，横截面上的正应力分布与半径的平方成反比，与最大半径的平方成正比。

因此，在圆轴纯扭转时，如果最大半径增大，横截面上的正应力分布会变得更加平均；如果半径增大，横截面上的正应力分布会变得更加集中。

结论圆轴纯扭转时，横截面上的正应力是一个重要的研究对象。

它与扭矩、半径和极惯性矩等因素密切相关，其分布规律是一个圆周分布。

研究圆轴纯扭转时横截面上的正应力，可以为工程设计和实际应用提供重要的参考依据。

圆轴受扭转变形时,最大剪应力
圆轴受扭转变形时的最大剪应力是指圆轴扭转变形，使得其轴线材料在分布式外侧受力方向上出现最大的剪应力。

总体说来，这一剪应力主要取决于圆轴转角及周围环境物理参数的变化。

一般情况下，当圆轴扭转变形时，随着轴线材料离心力的增加，其受力的剪应力会随之增加。

而随着转角的增大，轴线材料从它的中心到远离它的外面，其处在不同的位置处的剪应力也会随之增大，从而最终使得其外侧的剪应力达到最大值。

因此，圆轴受扭转变形时的最大剪应力取决于轴线材料受力的离心力和转角的大小。

此外，圆轴受扭转变形时的最大剪应力还受到材料本身的物理参数变化的影响。

例如，材料的弹性模量、拉伸强度、屈服强度都可以对应影响圆轴受扭转变形时的最大剪应力。

当材料弹性模量增大时，圆轴受扭转变形时的最大剪应力会降低；当材料拉伸强度增加时，受力的剪应力也会增大；当材料的屈服强度增大时，圆轴受扭转变形时的最大剪应力也会增加。

总之，圆轴受扭转变形时的最大剪应力是由轴线材料的受力离心力及转角的大小以及材料的物理参数变化来决定的。

这一剪应力的大小对于设计工程的安全性及质量有着重要的意义，因此，在进行设计工程之前，应当对这一剪应力进行准确评估，以确保工程的安全性及质量。

130一、讨论圆轴扭转时的应力状态，并分析铸铁试件受扭时的破坏现象。

解 根据第十九章讨论，圆轴扭转时，在横截面的边缘处剪应力最大，其数值为:n n W M=τ (e )在圆轴的最外层，按图22-5(a )，所示方式取出单元体ABCD ，单元体各面上的应力如图22-5(b )所示。

在这种情况下，ττσσ===xy y x ，0 （f ）单元体侧面上只有剪应力作用，而无正应力作用的这种应力状态称为纯剪切应力状态。

把(f )式代入公式(22-6)得:min maxσσ ττσσσσ±=+-±+=22)2(2xy y x y x 由公式（22-5）：yx xytg σστα--=220 →∞-所以 2709020--=或α450-=α 或 1350-=α以上结果表明，从x 轴量起，由 450-=α(顺时针方向)所确定的主平面上的主应力为max σ；而由 1350-=α所确定的主平面上的主应力为min σ。

按照主应力的记号规定：τσσστσσ-=====min 32max 10所以，纯剪切是二向应力状态，两个主应力的绝对值相等，都等于剪应力τ，但一个为拉应力，一个为压应力。

圆截面铸铁试件扭转时，表面各点max σ所在的主平面联成倾角为︒45的螺旋面[图22-5（a ）]。

由于铸铁抗拉强度较低，试件将沿这一螺旋面因拉伸而发生断裂破坏，如(a )(c ) 图22-5131图22-5（c ）所示。

二、 图22-6（a ）所示为一横力弯曲下的梁，求得截面m －n 上的弯矩M 及剪力Q 后，算出截面上一点A 处弯曲正应力和剪应力分别为：MPa MPa 50,70=-=τσ[图22-6（b ）]试确定A 点处的主应力及主平面的方位，并讨论同一横截面上其它点处的应力状态。

解 把从A 点处截取的单元体放大如图22-6（c ）所示。

选定x 轴的方向垂直向上，则0=x σ MPa y 70-=σ MPa xy 50-=τ由公式（22-5）得： 429.1)70(0)50(2220=----=--=yx xytg σστα︒=5520α或︒235 ︒=5.270α或︒5.117从x 轴量起，按逆时针方向量取的角度︒5.27，确定max σ所在主平面，以同一方向量取的角度,5.117︒确定min σ所在的另一主平面。