圆轴扭转横截面上的应力

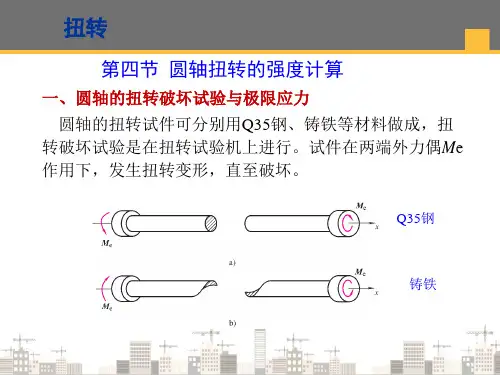
圆轴扭转的受力特点和变形特点
圆轴在受到扭矩作用时，其受力特点和变形特点与直轴不同。

下面我们来详细探讨一下圆轴扭转的受力特点和变形特点。

一、受力特点
在圆轴扭转过程中，受到的力主要是扭矩。

扭矩是使物体产生转动的力，其大小可以用公式T=FT*d来计算，其中T是扭矩，F是力，T是距离，d是轴的直径。

在圆轴扭转时，扭矩会使圆轴上的横截面产生剪切应力，剪切应力的大小与扭矩成正比。

二、变形特点
圆轴在受到扭矩作用时，会产生扭转变形。

这种变形主要表现为圆轴的各个横截面发生相对转动。

在圆轴扭转时，横截面之间的距离保持不变，因此不会出现拉伸或压缩变形。

同时，由于圆轴的刚度较大，所以扭转变形量相对较小。

三、影响圆轴扭转的因素
圆轴的扭转性能受到多种因素的影响，包括材料性质、截面形状、尺寸和边界条件等。

例如，圆轴的材料强度越高，其抵抗扭矩的能力就越强；截面形状和尺寸也会影响圆轴的扭转性能；边界条件如支撑条件和固定方式也会对圆轴的扭转性能产生影响。

四、圆轴扭转的应用
圆轴的扭转性能在机械工程中有着广泛的应用。

例如，在汽车和自行车中，车轴就是一种圆轴，它们需要承受来自轮子和车轮的扭矩。

在设计这些车轴时，需要考虑其受力特点和变形特点，以确保其具有足够的强度和刚度。

此外，在建筑工程和桥梁工程中，钢结构和钢筋混凝土结构的连接节点也需要利用圆轴的扭转性能来传递力和转矩。

130一、讨论圆轴扭转时的应力状态，并分析铸铁试件受扭时的破坏现象。

解 根据第十九章讨论，圆轴扭转时，在横截面的边缘处剪应力最大，其数值为:n n W M=τ (e )在圆轴的最外层，按图22-5(a )，所示方式取出单元体ABCD ，单元体各面上的应力如图22-5(b )所示。

在这种情况下，ττσσ===xy y x ，0 （f ）单元体侧面上只有剪应力作用，而无正应力作用的这种应力状态称为纯剪切应力状态。

把(f )式代入公式(22-6)得:min maxσσ ττσσσσ±=+-±+=22)2(2xy y x y x 由公式（22-5）：yx xytg σστα--=220 →∞-所以 2709020--=或α450-=α 或 1350-=α以上结果表明，从x 轴量起，由 450-=α(顺时针方向)所确定的主平面上的主应力为max σ；而由 1350-=α所确定的主平面上的主应力为min σ。

按照主应力的记号规定：τσσστσσ-=====min 32max 10所以，纯剪切是二向应力状态，两个主应力的绝对值相等，都等于剪应力τ，但一个为拉应力，一个为压应力。

圆截面铸铁试件扭转时，表面各点max σ所在的主平面联成倾角为︒45的螺旋面[图22-5（a ）]。

由于铸铁抗拉强度较低，试件将沿这一螺旋面因拉伸而发生断裂破坏，如(a )(c ) 图22-5131图22-5（c ）所示。

二、 图22-6（a ）所示为一横力弯曲下的梁，求得截面m －n 上的弯矩M 及剪力Q 后，算出截面上一点A 处弯曲正应力和剪应力分别为：MPa MPa 50,70=-=τσ[图22-6（b ）]试确定A 点处的主应力及主平面的方位，并讨论同一横截面上其它点处的应力状态。

解 把从A 点处截取的单元体放大如图22-6（c ）所示。

选定x 轴的方向垂直向上，则0=x σ MPa y 70-=σ MPa xy 50-=τ由公式（22-5）得： 429.1)70(0)50(2220=----=--=yx xytg σστα︒=5520α或︒235 ︒=5.270α或︒5.117从x 轴量起，按逆时针方向量取的角度︒5.27，确定max σ所在主平面，以同一方向量取的角度,5.117︒确定min σ所在的另一主平面。

圆轴扭转应力计算公式在我们的力学世界里，圆轴扭转应力计算公式可是个相当重要的家伙！这就好比是打开机械工程大门的一把神秘钥匙。

想象一下，你手里拿着一根长长的圆轴，就像那种汽车传动轴，当它开始扭转转动的时候，内部就会产生应力。

而我们要搞清楚这应力到底有多大，就得依靠圆轴扭转应力计算公式。

这个公式是：τ = Tρ / Ip 。

其中，τ 表示的是扭转切应力，T 是扭矩，ρ 是所求应力的点到圆心的距离，Ip 则是极惯性矩。

先来说说扭矩 T 。

假设你正在拧一个巨大的螺丝，你使的那个劲儿就是扭矩。

扭矩越大，圆轴扭转时产生的应力也就越大。

比如说，在工厂里的大型机器中，那些传递巨大动力的轴，就得承受巨大的扭矩，所以对它们的材料和设计要求就特别高。

再看ρ ，也就是点到圆心的距离。

这就像是在圆轴这个大舞台上，离圆心越远的地方，应力就越大。

就好比在旋转木马的外圈，你感受到的离心力是不是比在内圈大多了？极惯性矩 Ip 呢，它反映了圆轴横截面抵抗扭转的能力。

横截面形状和尺寸不同，极惯性矩也就不同。

比如说，一根实心的圆轴和一根空心的圆轴，在相同的扭矩作用下，空心的可能因为极惯性矩小，而更容易产生较大的应力。

我记得有一次去工厂参观，看到工人们在检修一台大型的旋转设备。

工程师拿着图纸，嘴里不停地念叨着圆轴扭转应力的计算数值，然后指挥着工人更换某个部件。

我凑过去一看，原来那个部件所在的圆轴位置，由于长期承受较大的扭矩和应力，已经出现了细微的裂纹。

如果不及时更换，可能会导致整个设备出现故障，影响生产进度。

在实际的工程应用中，圆轴扭转应力计算公式可帮了大忙。

从汽车的传动轴，到飞机发动机的轴，再到大型船舶的螺旋桨轴，都得依靠这个公式来确保它们在工作时能够安全可靠地运转。

所以啊，别小看这个公式，它虽然看起来有点复杂，但却是机械工程领域中不可或缺的重要工具。

我们通过它，能够更好地设计和制造各种机械部件，让我们的生活变得更加便捷和高效。

总之，圆轴扭转应力计算公式就像是一位默默守护着机械世界的卫士，时刻保障着各种旋转设备的正常运行。