第五讲 异方差和自相关.

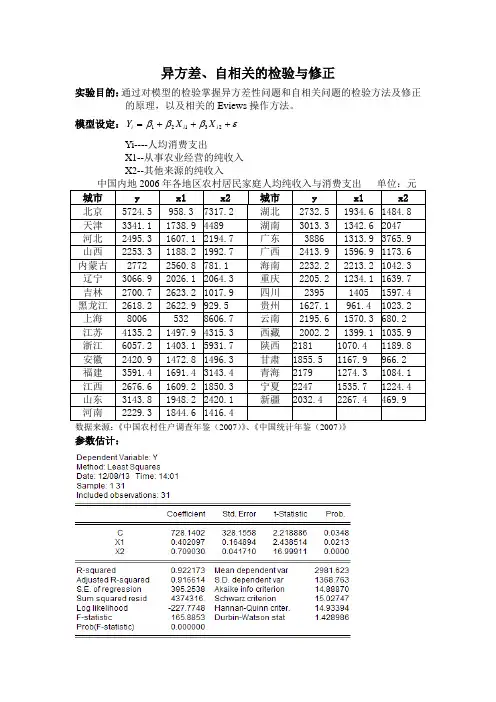
异方差、自相关的检验与修正实验目的：通过对模型的检验掌握异方差性问题和自相关问题的检验方法及修正的原理，以及相关的Eviews 操作方法。

模型设定：εβββ+++=23121i i i X X YYi----人均消费支出X1--从事农业经营的纯收入X2--其他来源的纯收入 中国内地2006年各地区农村居民家庭人均纯收入与消费支出 单位：元 城市 y x1 x2 城市 y x1 x2 北京 5724.5 958.3 7317.2 湖北 2732.5 1934.6 1484.8 天津 3341.1 1738.9 4489 湖南 3013.3 1342.6 2047 河北 2495.3 1607.1 2194.7 广东 3886 1313.9 3765.9 山西 2253.3 1188.2 1992.7 广西 2413.9 1596.9 1173.6 内蒙古 2772 2560.8 781.1 海南 2232.2 2213.2 1042.3 辽宁 3066.9 2026.1 2064.3 重庆 2205.2 1234.1 1639.7 吉林 2700.7 2623.2 1017.9 四川 2395 1405 1597.4 黑龙江 2618.2 2622.9 929.5 贵州 1627.1 961.4 1023.2 上海 8006 532 8606.7 云南 2195.6 1570.3 680.2 江苏 4135.2 1497.9 4315.3 西藏 2002.2 1399.1 1035.9 浙江 6057.2 1403.1 5931.7 陕西 2181 1070.4 1189.8 安徽 2420.9 1472.8 1496.3 甘肃 1855.5 1167.9 966.2 福建 3591.4 1691.4 3143.4 青海 2179 1274.3 1084.1 江西 2676.6 1609.2 1850.3 宁夏 2247 1535.7 1224.4 山东 3143.8 1948.2 2420.1 新疆 2032.4 2267.4 469.9 河南 2229.3 1844.6 1416.4 数据来源：《中国农村住户调查年鉴（2007）》、《中国统计年鉴（2007）》参数估计：估计结果如下：2709030.01402097.01402.728X X Y ++=Λ(2.218) (2.438) (16.999) 922173.02=R D.W.=1.4289 F=165.8853 SE=395.2538实验步骤：一、检查模型是否存在异方差1．图形分析检验(1)散点相关图分析分别做出X1和Y 、X2和Y 的散点相关图，观察相关图可以看出，随着X1、X2的增加，Y 也增加，但离散程度逐步扩大，尤其表现在X1和Y .这说明变量之间可能存在递增的异方差性。

自相关和异方差处理顺序引言自相关和异方差是时间序列分析中常见的两种问题，它们影响了模型的准确性和可靠性。

在进行时间序列建模时，需要处理这些问题，以确保模型的有效性。

本文将深入探讨自相关和异方差处理的顺序，并讨论不同处理顺序的影响。

什么是自相关和异方差自相关自相关是指时间序列中当前观测值与之前观测值之间的相关性。

它衡量的是时间序列中各个观测值之间的依赖关系。

自相关可以用自相关函数（ACF）图来表示，通过观察ACF图，可以判断时间序列是否存在自相关。

异方差异方差是指时间序列中方差不稳定的特征。

在时间序列中，方差可能随着时间的推移发生变化，这会导致模型的拟合不准确。

异方差可以用方差函数（VCF）图来表示，通过观察VCF图，可以判断时间序列是否存在异方差。

自相关和异方差处理的重要性自相关和异方差对时间序列建模的准确性和可靠性有重要影响，它们需要被处理以获得可靠的模型结果。

•自相关的存在会导致参数估计不准确，预测结果失真。

如果存在自相关，模型会无法捕捉到序列的真实动态，导致预测结果不准确。

•异方差使得模型的残差不符合正态分布，违背了建模的基本假设。

这会使得模型的显著性检验和置信区间估计不可靠，影响模型的有效性。

因此，为了获得可靠的模型结果，需要对自相关和异方差进行处理。

自相关和异方差处理顺序的影响自相关和异方差的处理顺序会对最终的模型结果产生影响。

不同的处理顺序可能导致不同的模型结构和参数估计。

先处理自相关后处理异方差如果先处理自相关再处理异方差，可能会导致如下影响：1.自相关处理可能会改变时间序列的动态特征。

当我们去除自相关时，可能会削弱序列中的一些重要信息，导致模型无法准确捕捉到序列的动态变化。

2.异方差处理可能会影响自相关的结构。

当我们对残差进行异方差处理时，可能会改变残差序列的结构，从而使得自相关的估计失真。

先处理异方差后处理自相关如果先处理异方差再处理自相关，可能会产生如下影响：1.异方差处理可能改变原始序列的动态特征。

七、 异方差与自相关一、背景我们讨论如果古典假定中的同方差和无自相关假定不能得到满足，会引起什么样的估计问题呢？另一方面，如何发现问题，也就是发现和检验异方差以及自相关的存在性也是一个重要的方面，这个部分就是就这个问题进行讨论。

二、知识要点1、引起异方差的原因及其对参数估计的影响2、异方差的检验（发现异方差）3、异方差问题的解决办法4、引起自相关的原因及其对参数估计的影响5、自相关的检验（发现自相关）6、自相关问题的解决办法 （时间序列部分讲解） 三、要点细纲1、引起异方差的原因及其对参数估计的影响原因：引起异方差的众多原因中，我们讨论两个主要的原因，一是模型的设定偏误，主要指的是遗漏变量的影响。

这样，遗漏的变量就进入了模型的残差项中。

当省略的变量与回归方程中的变量有相关关系的时候，不仅会引起内生性问题，还会引起异方差。

二是截面数据中总体各单位的差异。

后果：异方差对参数估计的影响主要是对参数估计有效性的影响。

在存在异方差的情况下，OLS 方法得到的参数估计仍然是无偏的，但是已经不具备最小方差性质。

一般而言，异方差会引起真实方差的低估，从而夸大参数估计的显著性，即是参数估计的t 统计量偏大，使得本应该被接受的原假设被错误的拒绝。

2、异方差的检验 （1）图示检验法由于异方差通常被认为是由于残差的大小随自变量的大小而变化，因此，可以通过散点图的方式来简单的判断是否存在异方差。

具体的做法是，以回归的残差的平方2i e 为纵坐标，回归式中的某个解释变量i x 为横坐标，画散点图。

如果散点图表现出一定的趋势，则可以判断存在异方差。

（2）Goldfeld-Quandt 检验Goldfeld-Quandt 检验又称为样本分段法、集团法，由Goldfeld 和Quandt 1965年提出。

这种检验的思想是以引起异方差的解释变量的大小为顺序，去掉中间若干个值，从而把整个样本分为两个子样本。

用两个子样本分别进行回归，并计算残差平方和。

1.5 假定条件的不成立用OLS 法得到的估计模型通过统计检验后，还要检验摸型是否满足假定条件。

由1.3 节知，只有模型的4个假定条件都满足时，用OLS 法得到的估计量才具有最佳线性无偏特性。

当一个或多个假定条件不成立时，OLS 估计量将丧失上述特性。

本节讨论当假定条件不成立时，对参数估计带来的影响以及相应的补救措施。

以下讨论都是在某一个假定条件被违反，而其他假定条件都成立的情况下进行。

分为5个步骤。

（1）回顾假定条件。

（2）假定条件不成立对模型参数估计带来的影响。

（3）定性分析假定条件是否成立。

（4）假定条件是否成立的检验（定量判断）。

（5）假定条件不成立时的补救措施。

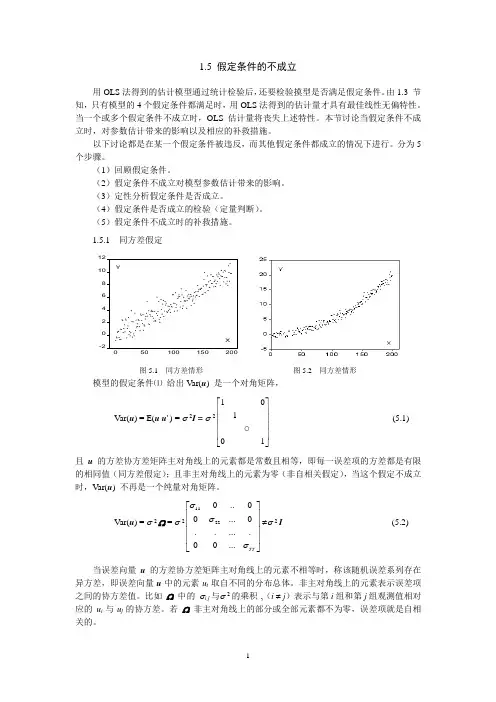
1.5.1 同方差假定-224681012050100150200XY图5.1 同方差情形 图5.2 同方差情形模型的假定条件⑴ 给出V ar(u ) 是一个对角矩阵， Var(u ) = E(u u ' ) = σ 2I = σ 21011⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦(5.1) 且u 的方差协方差矩阵主对角线上的元素都是常数且相等，即每一误差项的方差都是有限的相同值（同方差假定）；且非主对角线上的元素为零（非自相关假定），当这个假定不成立时，Var(u ) 不再是一个纯量对角矩阵。

Var(u ) = σ 2 Ω = σ 211220..00...0 00...TT σσσ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦≠σ 2 I (5.2)当误差向量u 的方差协方差矩阵主对角线上的元素不相等时，称该随机误差系列存在异方差，即误差向量u 中的元素u t 取自不同的分布总体。

非主对角线上的元素表示误差项之间的协方差值。

比如 Ω 中的 σi j 与σ 2的乘积 ,（i ≠ j ）表示与第i 组和第j 组观测值相对应的u i 与 u j 的协方差。

若 Ω 非主对角线上的部分或全部元素都不为零，误差项就是自相关的。

本节讨论异方差。

下一节讨论自相关问题。

第五讲、自相关1、自相关的概念：古典线性回归中假设扰动项u i中不存在自相关，即E(u i u j)=0, i≠j这表明任一观察值的扰动项不受其他观察值的扰动项的影响。

但是如果存在E(u i u j) ≠0, i≠j表明存在自相关问题。

自相关通常与时间序列数据有关，但截面数据中也可能产生自相关的问题（空间相关），例如，某一家庭消费支出的增加可能影响不愿比别人逊色的另一家庭消费支出的影响。

图a-d表明扰动项u存在可辨别的模式（可能存在自相关），而图e则表明不存在系统模式（可能不存在自相关）。

2、导致自相关的因素：（1）在涉及时间序列数据的回归方程中，大多数经济时间序列数据的一个显著特征是“惯性”或“延迟性”。

如GDP、就业、货币供给等时间序列都呈现周期性，连续的观察值之间很可能存在相互依赖或是相关的。

（2）模型设定错误：应该包括在模型中的重要变量未包括进模型（过低设定）或模型选择了错误的函数形式，这时残差会呈现出系统模式。

（3）蛛网现象：即解释变量是时间滞后变量，即具有时间滞后效应。

如农产品供给模型中价格对供给的影响存在蛛网现象（滞后效应）。

这种情况下的扰动项不是随机的。

（4）数据加工：在实证研究中，通常原数据是要经过加工的。

例如季度数据的时间序列回归中，数据通常是由月度数据按季相加再平均得到，而这种“平滑”过程的本身可能导致扰动项的系统模式，从而产生自相关。

3、自相关的后果：（1）虽然最小二乘估计仍然是线性和无偏的，但不是有效的，即最小二乘估计量(OLS)不是最优线性无偏估计量(BLUE)。

（2）OLS估计量的方差是有偏的，计算OLS估计量的方差或标准差的公式可能严重低估真实的方差或标准差，从而导致常用的t检验和F检验是不可靠的。

（3）通常计算的R2也是不可靠的。

4、自相关的诊断自相关的诊断存在异方差诊断中的类似问题，即ui是无法观察的，而且也不知道其产生机制：我们通过OLS估计，仅仅得到的是ei，通过对ei的讨论来“了解”自相关是否存在。

自相关和异方差处理顺序在统计学和计量经济学中，自相关和异方差是两个常见的问题，需要进行相应的处理才能保证模型的准确性和可靠性。

本文将以人类的视角，采用准确的中文进行描述，详细介绍自相关和异方差的处理顺序及其重要性。

一、自相关处理自相关是指时间序列数据中观测值之间存在的相关性。

当序列中的观测值之间存在一定的相关性时，会导致统计模型的参数估计不准确，假设检验无效，预测结果不可靠。

因此，需要进行自相关的处理。

自相关处理的一种常见方法是使用自相关函数（ACF）和偏自相关函数（PACF）进行分析。

ACF表示观测值与不同滞后期的观测值之间的相关性，PACF表示观测值与滞后期观测值之间的相关性，探究观测值之间的相关性结构。

在进行自相关处理时，可以采取以下步骤：1. 绘制时间序列图，观察序列的趋势和波动性。

2. 进行序列的平稳性检验，确保序列满足平稳性的要求。

3. 绘制ACF和PACF图，分析观测值之间的相关性结构。

4. 根据ACF和PACF的图形特征，选择合适的自回归移动平均模型（ARMA模型）。

5. 估计模型参数，进行模型拟合。

6. 检验模型的残差序列是否存在自相关，如果存在，则返回第3步，重新选择模型。

通过以上步骤，可以有效地处理自相关问题，提高模型的准确性和可靠性。

二、异方差处理异方差是指随着自变量的变化，因变量的方差也发生变化。

当存在异方差时，会导致模型的参数估计不准确，假设检验无效，预测结果不可靠。

因此，需要进行异方差的处理。

异方差处理的一种常见方法是使用加权最小二乘法（Weighted Least Squares, WLS）。

WLS是一种在回归分析中常用的方法，通过对误差项进行加权，降低异方差对回归结果的影响。

在进行异方差处理时，可以采取以下步骤：1. 绘制残差图，观察残差的分布特征。

2. 进行异方差检验，判断是否存在异方差。

3. 如果存在异方差，可以使用加权最小二乘法进行回归估计。

4. 根据异方差的特点，选择合适的加权函数，对误差项进行加权。

【推荐】stata基本操作汇总——异方差、自相关、多重共线性前言：计量经济学服务中心为大家罗列汇总出了关于异方差、自相关、多重共线性相关的知识，推荐收藏。

●●●学术利剑Stata ：论文中数据分析的一把利剑学术论文分析利剑 Stata的简介异方差Stata检查是否存在异方差的方法：1、看残差图，模型回归之后使用即可rvfplot（残差与拟合值的散点图）rvpplot（残差与解释变量的的散点图）2、White检验其基本命令是在完成基本的OLS 回归之后，输入imtest， white如果输出的P-Value 显著小于0.05，则拒绝原假设，即不存在异方差性3、BP(Breusch and Pagan,1979)检验关于stata处理异方差问题的命令基本命令是：estat hettest var1 var2 var3其中，var1 var2 var3 分别为你认为导致异方差性的几个自变量。

是你自己设定的一个滞后项数量。

同样，如果输出的P-Value 显著小于0.05，则拒绝原假设，即不存在异方差性。

estat hettest（默认设置使用拟合值y_hat）estat hettest（使用方程邮编的解释变量，而不是y_hat）estat hettest varlist（指定使用某些解释变量）解决办法方法一：WLSWLS是GLS（一般最小二乘法）的一种，也可以说在异方差情形下的GLS就是WLS。

在WLS下，我们设定扰动项的条件方差是某个解释变量子集的函数。

之所以被称为加权最小二乘法，是因为这个估计最小化的是残差的加权平方和，而上述函数的倒数恰为其权重。

在stata中实现WLS的方法如下：reg （被解释变量）（解释变量1）（解释变量2）…… [aweight=变量名]其中，aweight后面的变量就是权重，是我们设定的函数。

一种经常的设定是假设扰动项的条件方差是所有解释变量的某个线性组合的指数函数。

在stata中也可以方便地实现：首先做标准的OLS回归，并得到残差项；reg （被解释变量）（解释变量1）（解释变量2）……predict r, resid生成新变量logusq，并用它对所有解释变量做回归，得到这个回归的拟合值，再对这个拟合值求指数函数；gen logusq=ln(r^2)reg logusq (解释变量1) （解释变量2）……predict g, xbgen h=exp(g)最后以h作为权重做WLS回归；reg （被解释变量）（解释变量1）（解释变量2）…… [aweight=h]如果我们确切地知道扰动项的协方差矩阵的形式，那么GLS估计是最小方差线性无偏估计，是所有线性估计中最好的。

自相关和异方差处理顺序自相关和异方差是统计学中常见的两个问题，它们在数据分析和建模中起着重要的作用。

在本文中，我们将讨论自相关和异方差的处理顺序，并介绍一些常用的方法和技巧。

一、自相关的处理自相关是指同一时间序列数据中不同时间点之间的相关性。

在时间序列分析中，我们经常会遇到自相关的问题，这会影响到模型的准确性和可靠性。

为了解决自相关问题，我们可以采取以下几种方法：1. 平稳化处理：对于非平稳的时间序列数据，我们可以通过差分、对数变换或者其他方法来使其变得平稳。

平稳化后的数据能够更好地满足模型的假设条件，从而减小自相关的影响。

2. 引入滞后项：在建立模型时，我们可以引入滞后项来考虑时间序列数据中不同时间点之间的相关性。

常用的方法有自回归（AR）模型和移动平均（MA）模型等。

3. 模型诊断：在建立模型后，我们需要对模型进行诊断，检验是否存在自相关。

常用的方法有自相关图和部分自相关图等。

如果发现存在自相关，我们可以进一步调整模型的参数或者引入其他变量来解决自相关问题。

二、异方差的处理异方差是指同一时间序列数据中不同时间点之间方差不相等的现象。

异方差会导致模型的预测结果不准确，因此需要进行处理。

以下是一些处理异方差的方法：1. 变换方法：对于存在异方差的数据，我们可以通过对数变换、平方根变换或者倒数变换等方法来使其变得更加稳定。

变换后的数据能够更好地满足模型的假设条件，从而减小异方差的影响。

2. 加权最小二乘法：在建立模型时，我们可以采用加权最小二乘法来解决异方差问题。

加权最小二乘法能够根据不同时间点的方差大小来调整模型的参数，从而减小异方差的影响。

3. 残差诊断：在建立模型后，我们需要对模型的残差进行诊断，检验是否存在异方差。

常用的方法有残差图和方差稳定性检验等。

如果发现存在异方差，我们可以进一步调整模型的参数或者引入其他变量来解决异方差问题。

自相关和异方差是统计学中常见的问题，它们在数据分析和建模中起着重要的作用。