PB y
31
第32页/共42页
a
mB g
mA mB mC 2
解 得
FT1
mA
mAmB g mB mC
2
FT2
(mA mC 2)mB g mA mB mC 2
A mA
mC 0时: FT1 FT2
32
第33页/共42页
C mC
mB B
FT1
mA
mAmB g mB mC
2
FT2
(mA mC 2)mB g mA mB mC 2
的角加速度和角速度. M J
35
第36页/共42页
36
解: 受力分析,力矩(O)分析
重力对O点的力矩
M mgd
J
d L sin
2
有: 1 mgl sin J
2
m,l
O
θ
FN
mg
d
式中 J 1 ml2 3
得 3g sin
2l
第37页/共42页
由角加速度的定义
dω dω dθ ω dω
F
F
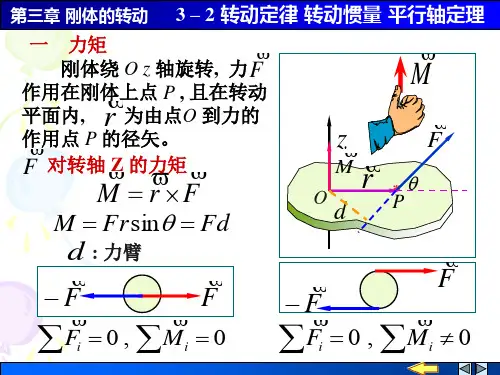
Fi 0 , Mi 0
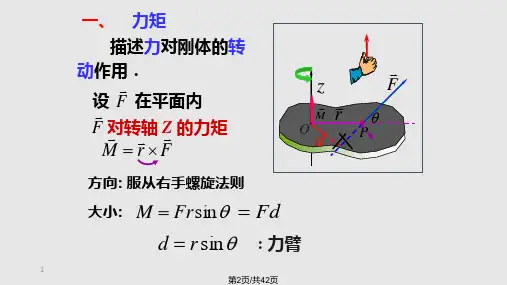
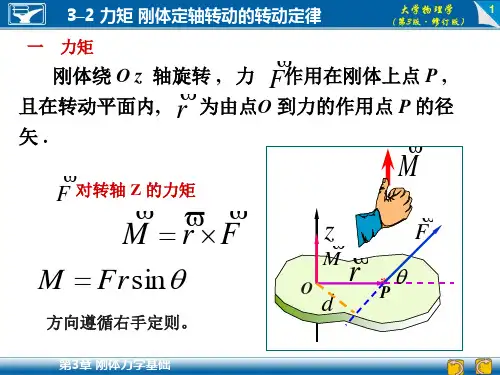
M rF
M Frsin Fd
3
第4页/共42页
4、一对力偶的力矩
M Fd
F
F
ol
F 0 M 0
F'
ro
F
F 0 M 0
M F l F l Fl
22
M Fr Fr 0
4
第5页/共42页
讨论
(1)若力 F 不在转动平面内,把力分
解为平行和垂直于转轴方向的两个分量
如令 mC 0 ,可得
A mA
FT1
FT2