大学物理-力矩、转动定律、转动惯量
- 格式:ppt
- 大小:886.00 KB
- 文档页数:30




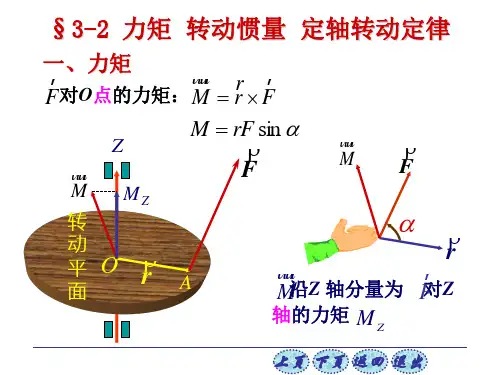





2-3 力矩转动定律转动惯量求摩擦力对y 轴的力矩解在定轴转动中,力矩可用代数值进行计算例如2. 刚体对定轴的转动定律在国际单位中k = 1刚体的转动定律讨论(2) 力矩相同,若转动惯量不同,产生的角加速度不同(3) 与牛顿定律比较:3. 转动惯量刚体绕给定轴的转动惯量J 等于刚体中每个质元的质量与该质元到转轴距离的平方的乘积之总和。
定义式质量不连续分布质量连续分布物理意义转动惯量是描述刚体在转动中的惯性大小的物理量。
它与刚体的形状、质量分布以及转轴的位置有关。
计算转动惯量的三个要素:(1)总质量;(2)质量分布;(3)转轴的位置(1) J 与刚体的总质量有关例如两根等长的细木棒和细铁棒绕端点轴转动惯量(2) J 与质量分布有关例如圆环绕中心轴旋转的转动惯量例如圆盘绕中心轴旋转的转动惯量(3) J 与转轴的位置有关4 平行轴定理例均匀细棒的转动惯量(2) (薄板)垂直轴定理x,y 轴在薄板内;z 轴垂直薄板。
例如求对圆盘的一条直径的转动惯量已知(3) 几种刚体的转动惯量下面给出了一些常见刚体的转动惯量。
请注意在转动惯量的计算中,转轴位置的重要性。
5. 转动定律的应用举例例一轻绳绕在半径r =20 cm 的飞轮边缘,在绳端施以F=98 N 的拉力,飞轮的转动惯量J=0.5 kg·m2,飞轮与转轴间的摩擦不计,(见图) 求(1) 飞轮的角加速度(2) 如以重量P =98 N的物体挂在绳端,试计算飞轮的角加速解例一根长为l ,质量为m 的均匀细直棒,可绕轴O 在竖直平面内转动,初始时它在水平位置解取一质元重力对整个棒的合力矩等于重力全部集中于质心所产生的力矩对一有限过程从上式看到:外力对刚体所作的功等于合力矩对角位移的积分,它是力做的功在刚体转动中的特殊表现形式。
讨论(1) 合力矩的功(2) 力矩的功就是力的功。
(3) 内力矩作功之和为零3. 转动动能定理——力矩功的效果对于一有限过程绕定轴转动刚体在任一过程中动能的增量,等于在该过程中作用在刚体上所有外力所作功的总和。
