m σ= 2 πR ds = rdrdθ dm = σ ds = σ rdrdθ
dN = gdm = σ rgdrdθ df = dN = σ rgdrdθ dM f = rdf = σ r gdrdθ
2
M f = ∫ dM f = σ g ∫ dθ ∫ r 2 dr
0 0
2π
R
2 = mgR 3 M f = jβ 1 mR 2 2 4 g β = 3R 3R j=
三 转动惯量
J = ∑ mi ri
2
2
如果刚体连续分布
m:质点惯性的量度 : J:刚体惯性的量度 : 转动惯量是描述刚体在转动中的惯性大小的物理量 几种常见刚体的转动惯量: 有关推导详见教材 有关推导详见教材P120) 几种常见刚体的转动惯量:(有关推导详见教材 细棒 细棒
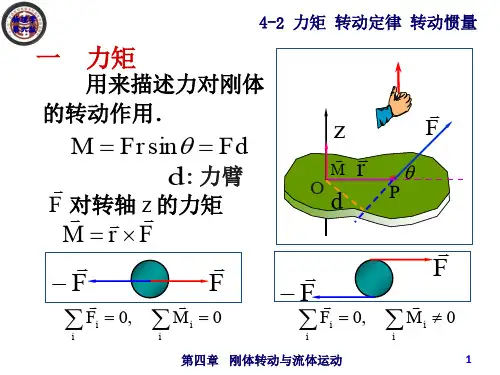
标量. 标量 J = ∫ r dm kg . m2,标量. r r 对比 F = m a M = Jβ
F2 =
r2
= j β = j dω dt cω = j dω dt dω = c dt ω j ω dω t c ∫ω0 ω =∫0 j dt
ct ω = ω0e j ct ω = ω0e j
M f = cω
练习18 练习
dθ = ω dt
t = c ln 2 j
= 1 ω0 2
jω0 c ln 2) (t = θ= j 2c θ = jω0 N= 2π 4π c
L m
1 J = mL2 + m1 L2 3
m1
质点 与刚 体组 合的 转动 惯量
R
m
r m1
1 J = mR 2 + m1 r 2 2
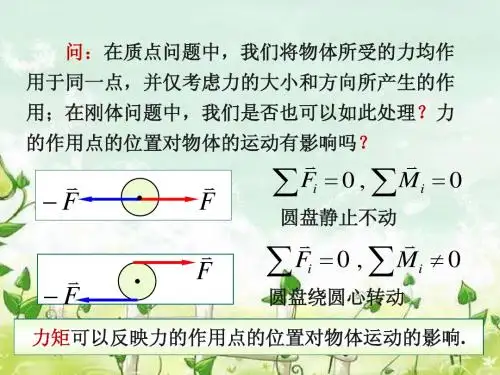
五,转动定律的应用 例1,一根轻绳跨过一定滑轮(滑轮 ,一根轻绳跨过一定滑轮( 视为圆盘), ),绳的两端分别 视为圆盘),绳的两端分别 悬有质量 为 m1 和 m2 的物体,m1 <m2 ,滑轮的 质量为 m ,半径为 R,所受的摩擦阻 , 绳与滑轮间无相对滑动. 力矩为 Mf ,绳与滑轮间无相对滑动. 试求:物体的加速度和绳的张力. 试求:物体的加速度和绳的张力. 已知: 已知: m1,m2 ,m, R ,Mf , 求: a , T1 , T2 解: 研究对象 m1 ,m2 ,m 建立坐标, 建立坐标,受力分析 如图 对m1 : 1 m1 g = m1a T 对m2: m 2 g T 2 = m 2 a