41转动惯量与转动定律

电机的转动惯量和转矩的关系
1 电机转动惯量和转矩的基本概念
电机的转动惯量指的是电机旋转时所表现出的惯性。

同样大小的
转动惯量会对不同大小的转矩产生不同的影响。

若转动惯量大，则给
定大小的转矩所产生的加速度就会小；而若转动惯量小，则同样大小
的转矩所产生的加速度就会大。

转矩指的是电机在旋转时对应用于轴上的力所产生的力矩。

一个
具有足够大的转矩的电机可以在一定程度上抵御阻力，而使旋转速度
不至于下降过快。

2 电机的转动惯量和转矩的关系
转动惯量和转矩之间的关系可以用牛顿第二定律来表示：F=ma。

其中，F为电机受到的作用力，m为电机的质量，a为加速度。

由于电
机受到的力是由转矩提供的，即F=T/r，其中T为转矩，r为轮子半径。

将电机的转动惯量记为J，则根据牛顿第二定律可得：
T = J * a / r
即，某一大小的转矩所产生的加速度与转动惯量成反比。

因此，
要在限制转矩的情况下增加电机的加速度，就需要减小电机的转动惯量。

另一方面，若要保持电机的加速度不变，可以通过增加转矩的大小来抵消转动惯量。

因此，一些需要较高加速度的机器人和机械装置通常使用低转动惯量的电机，同时加装较大转矩的减速器来调整其工作状态。

3 结语
转动惯量和转矩是电机中重要的机械参量，它们之间的关系对于电机的设计和性能优化具有重要的影响。

在实践应用中，需要根据具体的应用需求和工作环境来选择不同大小、不同类型的电机，以及相应的配套减速器、控制器等组件。

转动惯量定义转动惯量是物体旋转时的一个重要物理量，它描述了物体对于绕指定轴旋转的惯性大小。

在经典力学中，转动惯量通常用符号I表示。

转动惯量的定义是物体旋转时，质量分布对于绕轴旋转的惯性大小。

转动惯量的计算与物体的形状和质量分布有关。

对于具有规则形状的物体，可以通过简单的几何公式计算出转动惯量。

例如，对于一个围绕其对称轴旋转的均匀圆盘，其转动惯量可以通过公式I = 1/2MR^2计算，其中M是圆盘的质量，R是圆盘的半径。

类似地，对于其他规则形状的物体，也可以使用相应的几何公式来计算转动惯量。

然而，对于不规则形状的物体，计算转动惯量就变得更加复杂。

在这种情况下，可以使用积分来计算转动惯量。

通过将物体分解为无穷小的质量元，可以对每个质量元的转动惯量进行积分，并将所有质量元的转动惯量相加，从而得到整个物体的转动惯量。

转动惯量在物体旋转时起到了重要的作用。

根据牛顿第二定律，物体的转动惯量与物体所受的转动力矩之间存在着简单的关系。

转动力矩是物体在旋转过程中所受到的力矩，它可以通过 F = Iα来计算，其中F是力矩，I是转动惯量，α是物体的角加速度。

这个关系可以帮助我们理解物体在旋转中所受到的力矩大小与转动惯量的关系。

转动惯量还有许多实际应用。

在机械工程中，转动惯量是设计旋转部件和机械系统的重要参数。

通过准确计算转动惯量，可以确保机械系统的稳定性和性能。

在物理学中，转动惯量可以帮助我们理解刚体的旋转运动，以及天体运动中的转动规律。

转动惯量是描述物体旋转惯性大小的物理量。

它可以通过几何公式或积分计算得到，对于不同形状的物体有不同的计算方法。

转动惯量在物体旋转和力学系统设计中起着重要的作用，有助于我们理解和研究旋转运动的规律。

通过深入理解转动惯量的定义和计算方法，我们可以更好地理解旋转运动和力学系统的行为。

实验一转动定律和转动惯量平动和转动是物体的两种基本的机械运动。

转动定律是描述物体定轴转动的基本定律，转动惯量是反映物体改变转动状态的惰性程度。

转动惯量是刚体转动时惯性大小的量度，是表明刚体特性的一个物理量。

刚体转动惯量除了与物体质量有关外，还与转轴的位置和质量分布（即形状、大小和密度分布）有关。

如果刚体形状简单，且质量分布均匀，可以直接计算出它绕特定转轴的转动惯量。

对于形状复杂，质量分布不均匀的刚体，计算将极为复杂，通常采用实验方法来测定，例如机械部件、电动机转子和枪炮的弹丸等。

【一】实验目的1.加深对转动惯量的感性认识和对转动定律的理解。

2.用扭摆测定几种不同形状物体的转动惯量和弹簧的扭转常数，并与理论值进行比较。

3.用实验方法学习平行轴定理。

4.巩固用作图法处理实验数据。

【二】实验原理扭摆的构造如图（1）所示，在垂直轴1上装有一根薄片状的螺旋弹簧2，用以产生恢复力矩。

在轴的上方可以装上各种待测物体。

垂直轴与支座间装有轴承，以降低磨擦力矩。

3为水平仪，用来调整系统平衡。

将物体在水平面内转过一角度θ后，在弹簧的恢复力矩作用下物体就开始绕垂直轴作往返扭转运动。

根据虎克定律，弹簧受扭转而产生的恢复力矩M与所转过的角度θ成正比，即：θKM-=（l）式中，K为弹簧的扭转常数。

根据转动定律有：图（1）图（1）βI M =式中，I 为物体绕转轴的转动惯量，β为角加速度，由上式得：IM=β （2） 令2KIω=，忽略轴承的磨擦阻力矩，由（1）、（2）得： θωθθβ222-=-==I Kdtd上述方程表示扭摆运动具有角简谐振动的特性，角加速度与角位移成正比，且方向相反。

此方程的解为：)cos(φωθ+=t A式中，A 振动的角振幅，φ为初相位角，ω为角速度。

此谐振动的周期为：22T πω==可得：224πT K I = （3）由（3）可知，只要实验测得物体扭摆的摆动周期，并在I 和K 中任何一个量己知时即可计算出另一个量。

转动惯量的公式
转动惯量的公式是描述物体对转动运动的惯性大小的一个重要参数。

在物理学中，转动惯量通常用大写字母I表示，它与物体的质量分布以及物体对旋转轴的距离有关。

转动惯量的公式可以表示为I = Σmiri^2，其中Σ代表对所有质点求和，mi代表每个质点的质量，ri代表质点到旋转轴的距离。

转动惯量的公式对于描述物体在转动运动中的惯性特征非常重要。

通过计算转动惯量，我们可以了解物体对旋转的抵抗程度，即物体在转动过程中对外界施加的作用力所需的能量。

转动惯量的大小取决于物体的质量分布情况，质量分布越集中，转动惯量越小；质量分布越分散，转动惯量越大。

在实际应用中，转动惯量的公式可以帮助我们计算物体在转动运动中的角加速度、角速度以及角动量等物理量。

通过转动惯量的计算，我们可以更好地理解物体在转动运动中的行为规律，从而为工程设计和科学研究提供重要参考。

除了在理论物理中的应用，转动惯量的公式在工程领域也具有重要意义。

例如，在机械工程中，通过计算机械零件的转动惯量，可以帮助工程师设计出更加稳定和高效的机械系统。

在航天航空领域，转动惯量的计算也是设计飞行器和卫星轨道的重要依据之一。

总的来说，转动惯量的公式是描述物体对转动运动的惯性大小的重
要工具，它在物理学、工程学以及其他领域都具有广泛的应用价值。

通过深入理解转动惯量的公式，我们可以更好地认识物体在转动运动中的特性，为科学研究和工程实践提供有力支持。

转动惯量和转矩的关系转动惯量和转矩是刻画物体转动特性的重要物理量。

它们之间存在着密切的关系，转动惯量决定了转矩的大小和物体的转动加速度。

本文将从转动惯量和转矩的定义、计算公式、物理意义以及它们之间的关系等方面进行探讨。

一、转动惯量的定义和计算公式转动惯量是描述物体对转动运动的惯性大小的物理量。

它表示了物体绕某一轴旋转时，其质量分布对旋转的阻碍程度。

转动惯量的计算公式可以根据不同的几何形状和轴的位置来确定。

例如，对于质量均匀分布在轴上的细长杆，其转动惯量的计算公式为I=1/12 mL^2，其中m为杆的质量，L为杆的长度。

二、转矩的定义和计算公式转矩是描述物体受到外力作用时产生的转动效果的物理量。

它表示了物体受到外力作用时，绕某一轴发生转动的趋势。

转矩的大小等于力矩与力臂之积，力矩是力在垂直于力臂的方向上的分量，力臂是力的作用点到转轴的垂直距离。

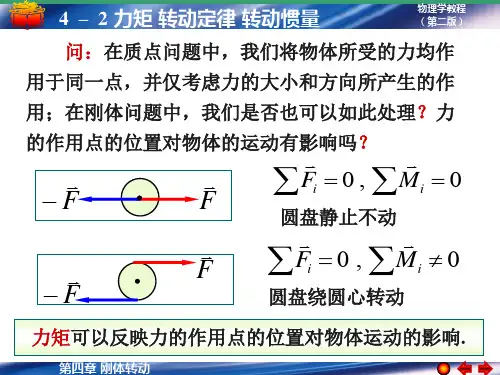
三、转动惯量和转矩的物理意义转动惯量和转矩都是描述物体转动特性的重要物理量，它们之间存在着密切的关系。

转动惯量表示了物体抵抗转动的能力，它越大，物体越不容易发生转动。

转矩则表示了物体受到外力作用时产生转动效果的大小，它越大，物体的转动越明显。

四、转动惯量和转矩的关系转动惯量和转矩的关系可以通过牛顿第二定律来描述。

根据牛顿第二定律，物体的转动加速度与作用在物体上的转矩成正比，与物体的转动惯量成反比。

具体而言，转矩等于转动惯量乘以转动加速度。

当物体所受的转矩为零时，根据转矩的定义可知，物体不会发生转动。

而当物体所受的转矩不为零时，根据牛顿第二定律可知，物体将产生转动加速度。

此时，转矩的大小与物体的转动惯量成反比，转动惯量越大，物体的转动加速度越小；转动惯量越小，物体的转动加速度越大。

转动惯量和转矩是描述物体转动特性的重要物理量，它们之间存在着紧密的关系。

转动惯量决定了物体对转动的抵抗程度，而转矩则表示了物体受到外力作用时产生的转动效果。

转动惯量和转矩之间的关系可以通过牛顿第二定律来描述，转矩等于转动惯量乘以转动加速度。

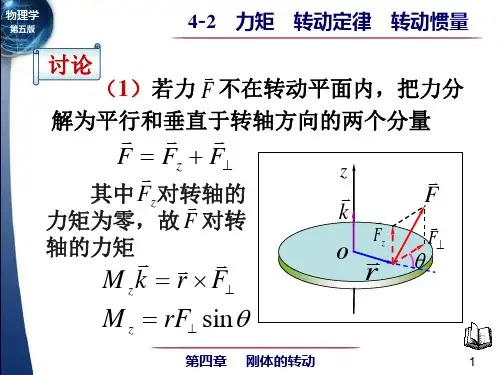
转动定律的推导 设刚体转动如图
作用在刚体上的外力为F ，取刚体上任一质量为m i 的小块。

把作用在该物块上的外力分解为两个方向上的力：径向力和切向力。

由于是刚体，物体不会发生形变，所以在径向不会产生运动。

忽略径向力的作用
对小物块运用牛顿第二定律有：ϕθsin cos i i i i it F F a m F ===
角标t 的含义为指明是作用中的切向力分量，
等号两边同乘r i ,有sin i i i it i Fr m a r ϕ=
将公式中的线量表达改写成角量，2sin i i i it i i i i i i Fr m a r m rr m r ϕββ===
其中sin i i Fr ϕ与力矩的定义吻合，所以公式可以改写为2i i i M m r β=
这是对刚体中的一个小质元的公式，考虑整个刚体，对上式两边求和有
2i i i
i i M m r β→∞→∞=∑∑ 公式左边为合外力矩。

令2i i mr J =∑，考虑到β与位置无关，上式改写为
M J β= ---1，
写为矢量形式 M J β= ---2
公式1，2即为刚体的转动定律，它是牛二定律在刚体转动问题上的变形。

∑∑∑∑===222222
12121r m r m m E i i i ik ωωv 22
1ωJ E k =。

实验 《利用刚体转动惯量实验仪验证转动定律》实验提要实验课题及任务物理实验室有多套刚体转动惯量实验仪，该实验设计有缺陷，实验误差较大，闲置多年不用。

在大学物理实验里，没有关于刚体定轴转动定律方面的实验。

为了使闲置仪器再次利用，同时填补刚体定轴转动定律方面的实验空白，要求学生设计一个“利用刚体转动惯量实验仪验证转动定律”的设计性实验。

本实验要求学生了解“刚体转动惯量实验仪实验”[参考附录]，利用实验室现有的气垫导轨实验用的A JSJ 3-型数字毫秒计及光电门，对刚体转动惯量实验仪进行改装，验证刚体定轴转动定律。

[提示：计算出合外力矩μM mgr M -='与β，当合外力矩μM mgr M -='与β成正比时，刚体定轴转动定律βI M =成立。

]学生根据自己所学的知识，并在图书馆或互联网上查找资料，设计出《利用刚体转动惯量实验仪验证转动定律》的整体方案，内容包括：（写出实验原理和理论计算公式，研究测量方法，写出实验内容和步骤），然后根据自己设计的方案，进行实验操作，记录数据，做好数据处理，得出实验结果，按要求写出完整的实验报告。

设计要求本实验要求学生自主完成四部分内容：一是完成刚体转动惯量实验仪的改装，二是自主设计实验原理及内容，三是估测阻力矩，四是验证刚体定轴转动定律。

实验仪器刚体转动惯量实验仪，A JSJ 3-型数字毫秒计，光电门 学时分配实验验收：3学时，在实验室内完成；教师指导(开放实验室)和开题报告：2学时。

提交整体设计方案时间学生自选题后2~3周内完成实验整体设计方案并提交。

提交整体设计方案，要求手写设计方案，字迹清晰，作图准确。

思考题如何才能提高实验的精确度？设计方案思路实验原理（很详细）一、如何验证刚体定轴转动定律1、刚体定轴转动定律：βI M =，有阻力矩μM 时：βμI M mgr =-2、如何验证刚体定轴转动定律成立：合外力矩为μM mgr M -='，若2121ββ≈''M M ，则刚体定轴转动定律成立。