第七章期权定价(金融工程学-中央财大,李磊宁)
- 格式:pptx
- 大小:528.20 KB
- 文档页数:35

金融学中的期权定价模型在金融学领域中,期权是一种金融工具,赋予持有人在未来某个特定时间以特定价格购买或出售标的资产的权利。
期权定价模型是为了确定期权合理价格的数学模型。
本文将介绍金融学中常用的期权定价模型,包括布莱克-斯科尔斯模型和风险中性定价模型。
布莱克-斯科尔斯模型(Black-Scholes Model)是最为著名和广泛使用的期权定价模型之一。
该模型于1973年由费舍尔·布莱克(Fisher Black)和米伦·斯科尔斯(Myron Scholes)共同提出,并获得了1997年诺贝尔经济学奖。
布莱克-斯科尔斯模型基于一系列假设,包括标的资产价格服从随机几何布朗运动、市场无摩擦、无交易成本等。
根据这些假设,该模型通过偏微分方程推导出了期权的定价公式。
该公式可以用来计算欧式期权的价格,在交易中发挥了重要的作用。
风险中性定价模型(Risk-Neutral Pricing Model)是另一种常用的期权定价模型。
该模型的基本原理是假设市场参与者对风险持中立态度,即市场对未来价格的期望值等于当前价格。
根据这个假设,风险中性定价模型通过建立与衍生品价格相关的风险中性测度,将期权的定价问题转化为风险中性测度下的期望值计算。
相对于布莱克-斯科尔斯模型,风险中性定价模型更加灵活,可以应用于更复杂的市场情况,并且可以解决了一些布莱克-斯科尔斯模型无法解决的问题。
除了布莱克-斯科尔斯模型和风险中性定价模型,金融学中还有其他的期权定价模型,如扩散模型、二叉树模型和蒙特卡洛模拟等。
这些模型都有各自的优势和适用范围,可以根据具体情况选择合适的模型进行期权定价。
需要注意的是,期权定价模型只是一种理论框架,模型的有效性和适用性需要在实践中进行验证。
实际应用中,投资者还需要考虑市场流动性、实际交易成本、波动率预测等因素,并结合自身的投资策略进行决策。
总结而言,金融学中的期权定价模型是为了计算期权的合理价格而设计的数学模型。

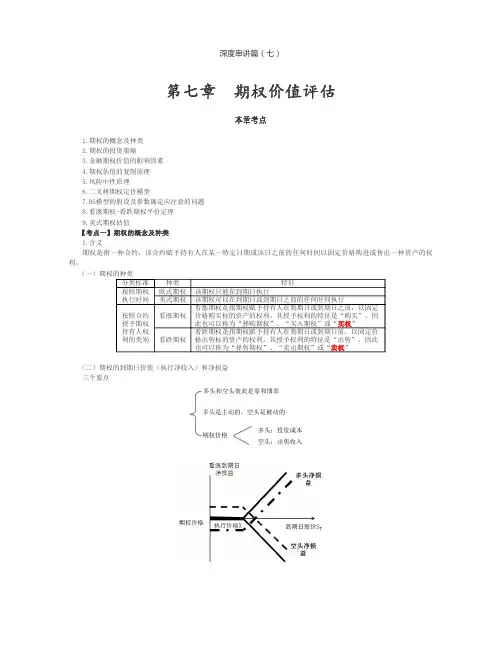
第七章期权价值评估(二)三、期权的投资策略(一)保护性看跌期权1.含义股票加看跌期权组合,称为保护性看跌期权。
是指购买1份股票,同时购买该股票1份看跌期权。
2.图示3.组合净损益组合净损益=执行日的组合收入-初始投资(1)股价<执行价格:执行价格-(股票投资买价+期权购买价格)(2)股价>执行价格:股票售价-(股票投资买价+期权购买价格)教材【例7-5】购入1股ABC公司的股票,购入价格S0=100元;同时购入该股票的1股看跌期权,执行价格X=100元,期权价格P=2.56元,1年后到期。
在不同股票市场价格下的净收入和损益,如表7-1和图7-5所示。
项目股价小于执行价格股价大于执行价格符号下降20%下降50%符号上升20%上升50%股票净收入S T8050S T120150期权净收入X-S T2050000组合净收入X100100S T120150股票净损益S T-S0-20-50S T-S02050期权净损益X-S T-P17.4447.440-P-2.56-2.56组合净损益X-S0-P-2.56-2.56S T-S0-P17.4447.444.特征锁定了最低净收入和最低净损益。
但是,同时净损益的预期也因此降低了。
【例题2·计算题】某投资人购入1份ABC公司的股票,购入时价格为40元;同时购入该股票的1份看跌期权,执行价格为40元,期权费2元,一年后到期。
该投资人预测一年股价变动幅度-20%-5%5%20%概率0.10.20.30.4要求:(1)判断该投资人采取的是哪种投资策略,其目的是什么?(2)确定该投资人的预期投资组合收益为多少?【答案】(1)股票加看跌期权组合,称为保护性看跌期权。
单独投资于股票风险很大,同时增加一个看跌期权,情况就会有变化,可以降低投资的风险。
(2)预期投资组合收益=0.1×(-2)+0.2×(-2)+0.3×0+0.4×6=1.8(元)。

期权定价理论知识期权定价理论是金融市场中重要的工具,它用于确定期权的合理价格。
期权是一种金融衍生品,它赋予持有者在未来某个时间点购买或卖出标的资产的权利,但并不强制执行。
期权的价格由多种因素决定,包括标的资产价格、行权价格、期权到期时间、标的资产的波动性以及无风险利率等。
在期权定价理论中,最著名的模型是布莱克-斯科尔斯期权定价模型(Black-Scholes Option Pricing Model)。
该模型是由费希尔·布莱克和米伦·斯科尔斯于1973年提出的,并且因此获得了诺贝尔经济学奖。
该模型基于一些假设,如市场是完全有效、无风险利率是恒定的等。
根据布莱克-斯科尔斯期权定价模型,期权的价格可以通过以下公式计算:C = S * N(d1) - X * e^(-rt) * N(d2)其中,C表示看涨期权价格,S表示标的资产价格,N(d1)和N(d2)分别是标准正态分布函数,X表示行权价格,r表示无风险利率,t表示期权到期时间。
公式中的d1和d2可以通过以下公式计算:d1 = (ln(S/X) + (r + (σ^2)/2)*t) / (σ * √t)d2 = d1 - σ * √t该模型通过考虑标的资产价格、行权价格、期权到期时间、标的资产的波动性和无风险利率等因素,来确定一个看涨期权的合理价格。
类似地,可以用类似的方法计算看跌期权的价格。
虽然布莱克-斯科尔斯期权定价模型是一个重要的理论框架,但它在实际应用中存在一些限制。
例如,该模型假设市场是完全有效的,但实际市场存在各种交易成本、税收和限制等,这些因素都可能影响期权的价格。
此外,该模型假设无风险利率是恒定的,但实际上利率是变化的。
因此,在实际应用中,需要根据实际情况进行调整和修正。
总之,期权定价理论是金融市场中重要的理论工具,它为期权的定价和交易提供了基础。
布莱克-斯科尔斯期权定价模型是其中最著名的模型之一,它通过考虑标的资产价格、行权价格、期权到期时间、标的资产的波动性和无风险利率等因素来确定期权的合理价格。




第七章期权价值评估(五)(二)二叉树期权定价模型1.单期二叉树定价模型(1)原理(风险中性原理的应用)(2)计算公式教材:期权价格=其中:上行概率=,下行概率=期权的价格=上行概率×C u/(1+r)+下行概率×C d/(1+r)教材【例7-10】假设ABC公司的股票现在的市价为50元。
有1股以该股票为标的资产的看涨期权,执行价格为52.08元,到期时间是6个月。
6个月以后股价有两种可能:上升33.33%,或者降低25%。
无风险利率为每年4%。
高顿财经CPA培训中心【例题11•计算题】假设甲公司的股票现在的市价为20元。
有1份以该股票为标的资产的看涨期权,执行价格为21元,到期时间是1年。
1年以后股价有两种可能:上升40%,或者降低30%。
无风险利率为每年4%。
要求:利用单期二叉树定价模型确定期权的价值。
【答案】期权价格=+==3.27(元)2.两期二叉树模型(1)基本原理:由单期模型向两期模型的扩展,不过是单期模型的两次应用。
教材【例7-11】继续采用[例7-10]中的数据,把6个月的时间分为两期,每期3个月。
变动以后的数据如下:ABC公司的股票现在的市价为50元,看涨期权的执行价格为52.08元,每期股价有两种可能:上升22.56%或下降18.4%;无风险利率为每3个月1%。
高顿财经CPA培训中心(2)方法:先利用单期定价模型,根据C uu和C ud计算节点C u的价值,利用C ud和C dd计算Cd的价值;然后,再次利用单期定价模型,根据C u和C d计算C0的价值。
从后向前推进。
3.多期二叉树模型(1)原理:从原理上看,与两期模型一样,从后向前逐级推进,只不过多了一个层次。
(2)股价上升与下降的百分比的确定:期数增加以后带来的主要问题是股价上升与下降的百分比如何确定问题。
期数增加以后,要调整价格变化的升降幅度,以保证年收益率的标准差不变。
高顿财经CPA培训中心把年收益率标准差和升降百分比联系起来的公式是:u=1+上升百分比=d=1-下降百分比=1/u其中:e=自然常数,约等于2.7183;标的资产连续复利收益率的标准差;T=以年表示的时段长度教材【例7-10】采用的标准差=0.4068u==1.3333该数值可以利用函数计算器直接求得,或者使用Excel的EXP函数功能,输入0.2877,就可以得到以e为底、指数为0.2877的值为1.3333.d=1/1.3333=0.75教材【例7-12】利用[例7-10]中的数据,将半年的时间分为6期,即每月1期。


