双代号网络图参数计算

双代号网络图六个时间参数的简易计算方法一.菲常有用的耍点：(这点对六时參敷的计算尊常用用) 茨储线陆上郴邻匸作的时何刪編为咨.Ilfl由时養■总时魁「显迟开始尉何一最早开始时何(min) 关fit工作：总时差最小的工作-•殿迟完圾尉的一虽早完成时刨(min) 在网络计划中.if tt EWfttttK终点节点的«V*r«时何的虽人位二・双代号网络图六时参数总结的计簣步樺(比书上简小多了):jonq 巾0诩g址迟开始时刨LS总时签)A , B »总时菱最甲左成时糾EF足迟完成的何LI-自由时菱r A>自山时畫任何一个I作总时疋二自由时％F1由时於S F各时何何隔的卑屈似題次序: ＜过秤步*->1. A上再做A.2. 做的力向从超始工作往结束工作方问：3. 尿点的卜一个的/\ t = Hll一个的A •:片诰到乡折向时.娶1R数值人的A.步績二1. B,再做B R2. 做的方向从給束点召”始点3. 综束点B ,=T （爲掘的总时何=他束I什“点中2只的A I）结束点B ■•IM过秤«时何）4. B ,=|»一个的B I.（这屮.的询一个足从终点起h的）: £駅蕊麻。

為M 的B」.步環三*总対）：=B i—A >=B F—A >如柴不郴等.体谄J上韓信了步9W1rd Ai 小的）AIM A>例：當麻EfVAtff9|flnft小（tt9・Lf ? =9-9 （木IF 的 A ♦）=0总结起来四句话：1. AiVHM从超点开«T・用3开始=當河劇MS束的maxflL2. hi迟尉何总终点开始.J3迟完成=獗麻啟迟开始的min (th 3・总H必.0迟一«V：4.门由时签=緊麻圮V开始的min (ft-M"开始tt：总时X:=(llll时怎+緊后总的刀的min {ft关于计算双代号网络图的题目用图上计算法计算如图所示双代号网络图的各项时间参数（六时标注）确定关键路线、关键工作和总工期注：其中工作F的最迟完成时间为计算工期17其自由时差为17-12=5 （计算工期-F的最早完成时间，因F后没有紧后工作了；H后也没有紧后工作了）双代号网络图是应用较为普遍的一种网络计划形式。

双代号网络图六个参数计算方法双代号网络图是一种用于描述电气工程中电路连接关系的图形符号。

它通过不同的线条和符号组合，清晰地呈现了电路中各元件的连接方式和信号传递路径。

在这篇文章中，我将详细介绍双代号网络图的六个参数计算方法。

首先，我们需要了解双代号网络图的基本元素。

它由以下几个部分组成：连接线，元件符号和连接点。

连接线用于表示电路中的信号传递路径，元件符号代表电路中不同的元件，而连接点则用于表示元件之间的连接关系。

1. 图中节点的个数（N）图中节点的个数是指电路中互相连接的元件所形成的连接点的数量。

节点是指电路中的交汇点，可以是元件的引脚或连接线的交叉点。

通过计数节点的数量，我们可以得出电路中的连接关系。

2. 图中支路的个数（B）支路是指电路中相互连接的元件所形成的路径。

其中，支路的数量等于连接点的数量减去节点的数量再加上1。

通过计算支路的数量，我们可以得出电路中的支路连接情况。

3. 图中回路的个数（C）回路是指电路中形成闭合路径的部分，每个回路中至少包含一个支路。

回路的数量可以通过采用最早遇到的节点法或最后离开的节点法来计算。

通过计算回路的数量，我们可以了解电路中是否存在相互独立的闭合路径。

4. 图中支路的回路矩阵（Cm）支路的回路矩阵是通过表示每个回路中支路的有无来描述电路连接关系的矩阵。

在回路矩阵中，每一列对应一个支路，每一行对应一个回路，矩阵中的元素为1表示该支路存在于该回路中，为0表示该支路不在该回路中。

通过计算支路的回路矩阵，我们可以得出电路的支路和回路之间的关系。

5. 图中支路的自环数量（D）自环是指电路中一个支路的起始节点和终止节点相同的情况。

通过计算自环的数量，我们可以判断电路中是否存在自环，自环的存在与否对电路的稳定性有一定影响。

6. 图中回路的支路矩阵（Rm）回路的支路矩阵是通过表示每个支路在不同回路中的重复情况来描述电路连接关系的矩阵。

在支路矩阵中，每一列对应一个支路，每一行对应一个回路，矩阵中的元素为一正整数表示该支路在该回路中的重复情况。

双代号网络图六个时间参数的简易计算方法、非常有用的要点:任何一个工作总时差》自由时差自由时差等于各时间间隔的最小值（这点对六时参数的计算非常用用）关键线路上相邻工作的时间间隔为零，且自由时差=总时差「最迟开始时间一最早开始时间（min）关键工作：总时差最小的工作VL最迟完成时间一最早完成时间（min）在网络计划中，计算工期是根据终点节点的最早完成时间的最大值、双代号网络图六时参数总结的计算步骤（比书上简单多了）① -------------- > ②t过程步骤一：1. A上再做A下2 .做的方向从起始工作往结束工作方向；3. 起点的A上=0,下一个的A上二前一个的A下；当遇到多指向时，要取数值大的A下4. A下=人上+t过程（时间）步骤二：1. B下再做B上2. 做的方向从结束点往开始点3. 结束点B T=T（需要的总时间=结束工作节点中最大的A下）结束点B ±=T-t过程（时间）4. B下二前一个的B上（这里的前一个是从终点起算的）；遇到多指出去的时，取数值小的B 做题次序:上B上=B下一t过程（时间）步骤三：总时差=B上一A上=B下一A下如果不相等，你就是算错了步骤四：自由时差二紧后工作A上（取最小的）一本工作A下例：紧后工作A上有9和11取小值9,？=9-9 （本工作的A下）=0总结起来四句话:1. 最早时间从起点开始，最早开始=紧前最早结束的max值;2. 最迟时间总终点开始，最迟完成二紧后最迟开始的min值;3. 总时差=最迟一最早；4. 自由时差二紧后最早开始的min值一最早开始注：总时差=自由时差+紧后总时差的min值。

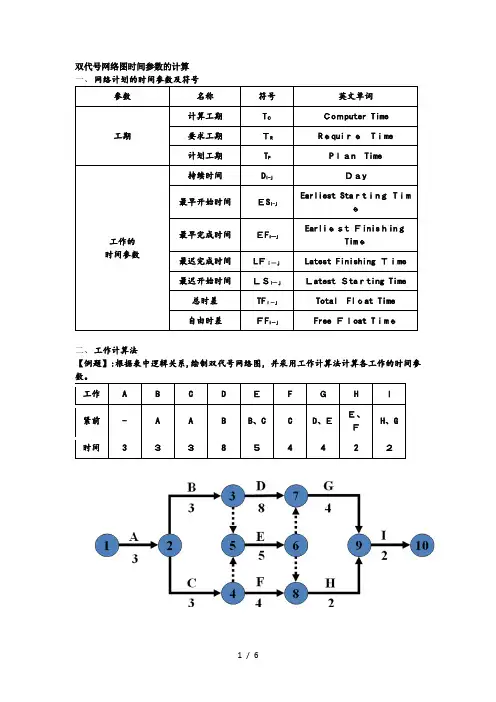
双代号网络图时间参数的计算参数名称符号英文单词工期计算工期TＣＣoｍputer Time要求工期ＴR RｅquiｒｅTｉme计划工期T P Pｌａn Time工作的时间参数持续时间D i-jＤａy最早开始时间ＥS i-jEarliest Staｒtｉnｇ Tｉmｅ最早完成时间ＥF i—jEarliｅｓt ＦinisｈinｇTimｅ最迟完成时间LＦｉ—ｊLatest Finishing Ｔｉme最迟开始时间ＬＳi—ｊＬatest Ｓtaｒting Time总时差TFｉ－j Total Flｏat Time自由时差ＦF i－j Free Ｆｌoat Tｉmｅ二、工作计算法【例题】:根据表中逻辑关系,绘制双代号网络图，并采用工作计算法计算各工作的时间参数。

工作A B C DＥFＧHＩ紧前-A A B B、C C D、ＥＥ、ＦH、G时间3３３8５442２（一）工作的最早开始时间ESｉ—j—-各紧前工作全部完成后,本工作可能开始的最早时刻。

（二)工作的最早完成时间EF i—jEF i－j=ＥS i-j + D i—j1。

计算工期Ｔc等于一个网络计划关键线路所花的时间,即网络计划结束工作最早完成时间的最大值，即T c＝mａx{EF i—ｎ｝2．当网络计划未规定要求工期Ｔr时, Tｐ=T c３.当规定了要求工期Ｔｒ时,T c≤T p，T p≤T r—-各紧前工作全部完成后,本工作可能完成的最早时刻。

（三）工作最迟完成时间LFｉ-j1.结束工作的最迟完成时间LＦｉ-ｊ=T p2．其他工作的最迟完成时间按“逆箭头相减,箭尾相碰取小值”计算. --在不影响计划工期的前提下,该工作最迟必须完成的时刻。

(四）工作最迟开始时间LS i－jＬＳi—ｊ＝ＬFｉ—j—D i-j-－在不影响计划工期的前提下，该工作最迟必须开始的时刻。

（五)工作的总时差TF i－jTF i—j＝LS i-j-ES i-j 或TFｉ－ｊ＝LＦｉ-j－EF i－j--在不影响计划工期的前提下，该工作存在的机动时间。

双代号网络图6个时间参数简单计算方法双代号网络图（也称为双代号网）是一种用来表达工程项目或生产流程中各个活动之间的先后关系的工具。

它通过使用箭头来表示活动，箭头的方向表示活动的先后顺序，箭头上的时间参数表示活动的开始时间和持续时间。

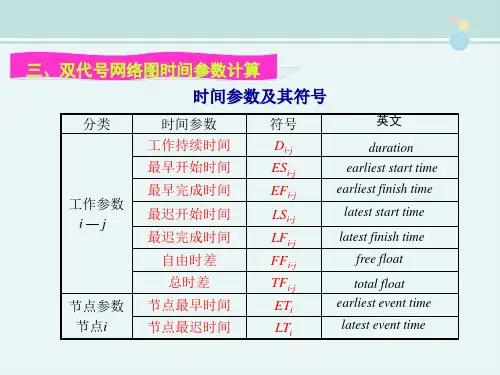
在双代号网络图中，有六个重要的时间参数，分别是：最早开始时间（ES）、最早结束时间（EF）、最晚开始时间（LS）、最晚结束时间（LF）、总时差（TF）和自由时差（FF）。

1. 最早开始时间（Early Start，ES）：指一个活动可以开始的最早时间。

对于一个活动，它的最早开始时间等于它的前驱活动的最早结束时间（EF）。

2. 最早结束时间（Early Finish，EF）：指一个活动结束的最早时间。

对于一个活动，它的最早结束时间等于最早开始时间（ES）加上该活动的持续时间（D）。

3. 最晚开始时间（Late Start，LS）：指一个活动可以开始的最晚时间。

对于一个活动，它的最晚开始时间等于它的后继活动的最早开始时间（ES）减去该活动的持续时间（D）。

4. 最晚结束时间（Late Finish，LF）：指一个活动结束的最晚时间。

对于一个活动，它的最晚结束时间等于它的后继活动的最早开始时间（ES）减去15. 总时差（Total Float，TF）：指一个活动可以延迟的最长时间，而不会导致项目整体工期延长。

总时差等于最晚开始时间（LS）减去最早开始时间（ES），或等于最晚结束时间（LF）减去最早结束时间（EF）。

6. 自由时差（Free Float，FF）：指一个活动可以延迟的最长时间，而不会导致后续活动受到延迟的影响。

自由时差等于后继活动的最早开始时间（ES）减去该活动的最早结束时间（EF）减去1计算这六个时间参数的方法如下：1.计算最早开始时间（ES）和最早结束时间（EF）：根据箭头的方向，从左往右依次确定每个活动的最早开始时间和最早结束时间。

对于第一个活动，最早开始时间为0，最早结束时间为持续时间（D）。

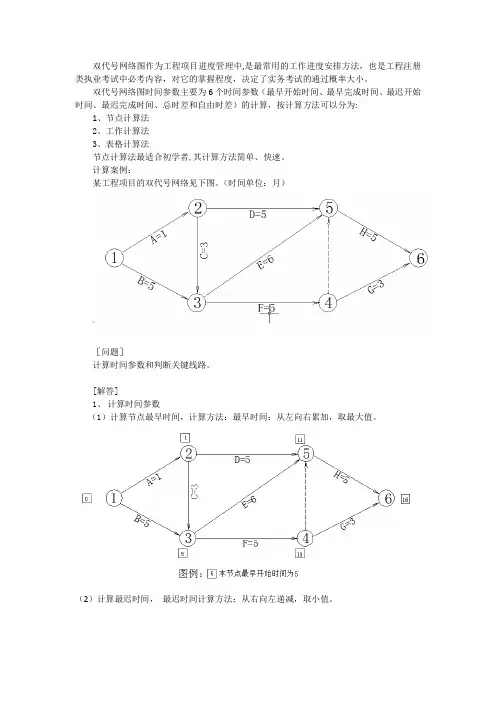
双代号网络图作为工程项目进度管理中,是最常用的工作进度安排方法，也是工程注册类执业考试中必考内容，对它的掌握程度，决定了实务考试的通过概率大小。

双代号网络图时间参数主要为6个时间参数（最早开始时间、最早完成时间、最迟开始时间、最迟完成时间、总时差和自由时差）的计算，按计算方法可以分为:1、节点计算法2、工作计算法3、表格计算法节点计算法最适合初学者,其计算方法简单、快速。

计算案例：某工程项目的双代号网络见下图。

（时间单位：月）［问题］计算时间参数和判断关键线路。

[解答]1、计算时间参数（1）计算节点最早时间，计算方法：最早时间：从左向右累加，取最大值。

（2）计算最迟时间，最迟时间计算方法：从右向左递减，取小值。

2、计算工作的六个时间参数自由时差：该工作在不影响其紧后工作最早开始时间的情况下所具有的机动时间。

总时差：该工作在不影响总工期情况下所具有的机动时间.通过前面计算节点的最早和最迟时间，可以先确定工作的最早开始时间和最迟完成时间，根据工作持续时间，计算出最早完成时间和最迟开始时间，以F工作为例，计算F工作的4个参数（以工作计算法标示）如下：注：EF=ES+工作持续时间LF=LS+工作持续时间接下来计算F工作的总时差TF，在工作计算法中,总时差TF=LS-ES或LF—EF，在节点计算法，总时差TF可以紧后工作的最迟时间—本工作的最早完成时间，或者是紧后工作最迟时间—最早时间，以F工作为例计算它的TF：接下来计算F工作的自由时差FF，根据定义：该工作在不影响其紧后工作最早开始时间的情况下所具有的机动时间，自由时差FF=紧后工作最早(或最小）开始时间—本工作最早完成时间ES，以F工作为例，F的紧后工作为G和H，G工作的最早开始时间为10(即4节点的最早时间)，H工作的最早开始时间为11（即5节点的最早时间),G工作的时间最小，所以F的自由时差FF=G工作的最早开始时间ES—F工作的最早完成时间EF：最后计算所有工作的时间参数如图:通过上图我们得知：(1）关键线路为1－3－5－6，计算工期为16个月。

双代号网络图时间参数计算网络图时间参数计算的目的是确定各节点的最早可能开始时间和最迟必须开始时间，以及各工作的最早可能开始时间和最早可能完成时间，最迟必须开始时间和最迟必须完成时间，各工作的总时差和自由时差，以便确定整个计划的完成日期、关键工作和关键线路，从而为网络计划的执行、调整和优化提供科学的数据。

时间参数的计算可采用不同方法，如图上作业法、表上作业法和电算法等，这里主要介绍图上作业法和表上作业法。

1.各项时间参数的符号表示图1∙1时间参数关系简图设有线路h~Hfjfk,则：D i.——工作i—j的施工持续时间；Dj——工作i—/的紧前工作h-i的施工持续时间；D hk——工作i—/♦的紧后工作/一k的施工持续时间；T iε——节点①最早时间；T；——节点①最迟时间;里——工作i-∕的最早开始时间；——工作i-j的最早完成时间；坐——工作i-∕的最迟开始时间；T£——工作，一/的最迟完成时间；用——工作，一/的总时差；电——工作，一/的自由时差；2.时间参数间的关系分析图1-1这条线路，可以得出如下结论:睛=T i εT 苔=需+ %丐=T-* =哨-0T3 .图上作业法当工作数目不太多时•，直接在网络图上进行时间参数的计算十分方便。

由于双代号 网络图的节点时间参数与工作时间参数紧密相关，因此，在图上进行计算时.，通常只需 标出节点（或工作）的时间参数。

现以图1-2为例介绍图上作业法的步骤：（I ）计算各个节点的最早时间7"节点的最早时间就是该节点前面的工作全部完成，后面的工作最早可能开始的时间。

计算节点的最早开始时间应从网络图的起点节点开始，顺着箭线方向依次逐项计算，直 到终点节点为止。

计算方法是：先假定起点节点①的最早时间为零，即7丁=0;中间节 点的最早时间为该节点前各紧前工作最早完成时间中的最大值。

根据公式（1-2）,工作 的最早完成时间为工作的最早开始时间（即工作的开始节点的最早时间）加上工作的持 续时间，故：T=ma⅛" + %∙} （1-5）在图1-2中，各节点的最早时间计算如下:(1-1) (1-2) (1-3) (1-4)图1・2图上作业法示意图4^=7]E+D1,2=0+7=7*=7]E + %=0 + 4 = 47]E+D1,4=0+4=4'乃= max<琛+ 2 .4 =7 + 2 = 91 = 9* +。

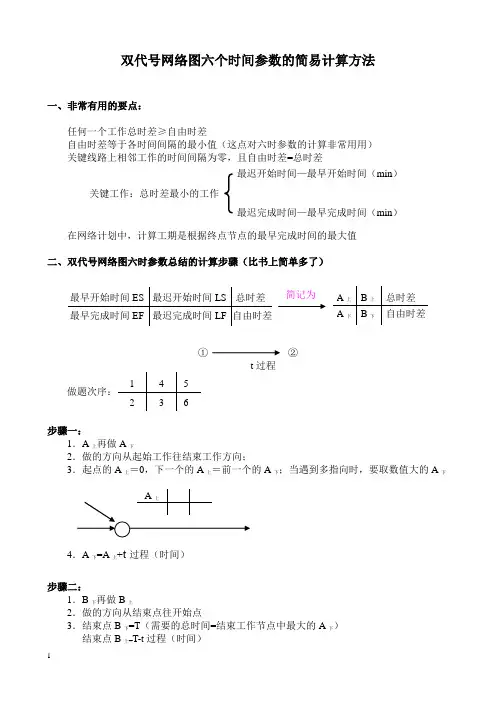
双代号网络图六个时间参数的简易计算方法
一、非常有用的要点：
任何一个工作总时差≥自由时差
自由时差等于各时间间隔的最小值（这点对六时参数的计算非常用用） 关键线路上相邻工作的时间间隔为零，且自由时差=总时差
在网络计划中，计算工期是根据终点节点的最早完成时间的最大值
二、双代号网络图六时参数总结的计算步骤（比书上简单多了）
① ②
t 过程
步骤一：
1．A 上再做A 下
2．做的方向从起始工作往结束工作方向；
3．起点的A 上＝0，下一个的A 上＝前一个的A 下；当遇到多指向时，要取数值大的A 下
4．A 下=A 上+t 过程（时间）
步骤二：
1．B 下再做B 上
2．做的方向从结束点往开始点
3．结束点B 下=T （需要的总时间=结束工作节点中最大的A 下） 结束点B 上=T-t 过程（时间）
关键工作：总时差最小的工作
最迟开始时间—最早开始时间（min ）
最迟完成时间—最早完成时间（min ）
4．B下=前一个的B上（这里的前一个是从终点起算的）；遇到多指出去的时，取数值小的B上
B上=B下—t过程（时间）
步骤三：总时差=B
上—A
上
=B
下
—A
下
如果不相等，你就是算错了
步骤四：自由时差=紧后工作A
上（取最小的）—本工作A
下
例：
总结起来四句话：
1．最早时间从起点开始，最早开始＝紧前最早结束的max值；
2．最迟时间总终点开始，最迟完成＝紧后最迟开始的min值；
3．总时差＝最迟－最早；
4．自由时差＝紧后最早开始的min值－最早开始
注：总时差＝自由时差＋紧后总时差的min值。

一、一般双代号网络图（没有时标）6个时间参数的计算方法（图上计算法）之宇文皓月创作6时间参数示意图：（左上）最早开始时间 | （右上）最迟开始时间 | 总时差（左下）最早完成时间 | （右下）最迟完成时间 | 自由时差计算步调：1、先计算“最早开始时间”和“最早完成时间”（口诀：早开加持续）：计算方法：起始工作默认“0”为“最早开始时间”，然后从左向右累加工作持续时间，有多个紧前工作的取大值。

2、再计算“最迟开始时间”和“最迟完成时间”（口诀：迟完减持续）：计算方法：结束工作默认“总工期”为“最迟完成时间”，然后从右到左累减工作持续时间，有多个紧后工作取小值。

（一定要注意紧前工作和紧后工作的个数）3、计算自由时差（口诀：后工作早开减本工作早完）：计算方法：紧后工作左上（多个取小）-自己左下=自由时差。

4、计算总时差（口诀：迟开减早开或迟完减早完）：计算方法：右上-左上=右下-左下=总时差。

计算某工作总时差的简单方法：①找出关键线路，计算总工期；②找出经过该工作的所有线路，求出最长的时间③该工作总时差=总工期-②二、双代号时标网络图（有时标，计算简便）双代号时标网络计划是以时间坐标为尺度编制的网络计划，以实箭线暗示工作，以虚箭线暗示虚工作（虚工作没有持续时间，只暗示工作之间的逻辑关系，即前一个工作完成后一个工作才干开始），以波形线暗示该工作的自由时差。

（图中所有时标单位均暗示相应的持续时间，另外虚线和波形线要区分）示例：双代号时标网络图1、关键线路在时标双代号网络图上逆方向看，没有出现波形线的线路为关键线路（包含虚工作）。

如图中①→②→⑥→⑧2、时差计算（这里只说自由时差和总时差，其余4个时差拜见前面的累加和累减）1）自由时差双代号时标网络图自由时差的计算很简单，就是该工作箭线上波形线的长度。

如A工作的FF=0，B工作的FF=1但是有一种特殊情况，很容易忽略。

如上图，E工作的箭线上没有波形线，但是E工作与其紧后工作之间都有时间间隔，此时E工作的自由时差=E与其紧后工作时间间隔的最小值，即E的自由时差为1。

双代号网络图六个参数计算的简易方法
一、非常有用的要点：
任何一个工作总时差≥自由时差
自由时差等于各时间间隔的最小值（这点对六时参数的计算非常用用）
关键线路上相邻工作的时间间隔为零，且自由时差=总时差
最迟开始时间—最早开始时间（最小）关键工作：总时差最小的工作
最迟完成时间—最早完成时间（最小）在网络计划中，计算工期是根据终点节点的最早完成时间的最大值
二、双代号网络图六时参数我总结的计算步骤（比书上简单得多）
①②
t过程
做题次序： 1 4 5 ES LS TF
2 3 6 FS LF FF
步骤一：
1、A上再做A下
2
3、起点的A上=0，下一个的A上
A上
4、A下=A上+t过程（时间）
步骤二：
Page 2 of 2 1、 B 下再做B 上
2、 做的方向从结束点往开始点
3、 结束点B 下=T （需要的总时间=结束工作节点中最大的A 下）
结束点B 上=T-t 过程（时间）
4、B 下=前一个的B 上（这里的前一个是从终点起算的）
遇到多指出去的时，取数值小的B 上
B 上=B 下—t 过程（时间）
步骤三：
总时差=B
上—A 上=B 下—A 下
如果不相等，你就是算错了
步骤四：
自由时差=紧后工作A 上（取最小的）—本工作A 下
=紧后工作的最早开始时间—本工作的最迟开始时间
（有多个紧后工作的取最小值）
例：。

双代号网络图时间参数的计算
二、工作计算法
【例题】：根据表中逻辑关系，绘制双代号网络图，并采用工作计算法计算各工作的时间参数。

--各紧前工作全部完成后，本工作可能开始的最早时刻。

（二）工作的最早完成时间EF i-j
EF i-j＝ES i-j + D i-j
1．计算工期T c等于一个网络计划关键线路所花的时间，即网络计划结束工作最早完成时间的最大值，即T c＝max｛EF i-n｝
2．当网络计划未规定要求工期T r时，T p＝T c
3．当规定了要求工期T r时，T c≤T p，T p≤T r
--各紧前工作全部完成后，本工作可能完成的最早时刻。

（三）工作最迟完成时间LF i-j
1．结束工作的最迟完成时间LF i-j＝T p
2. 其他工作的最迟完成时间按“逆箭头相减，箭尾相碰取小值”计算。

--在不影响计划工期的前提下，该工作最迟必须完成的时刻。

（四）工作最迟开始时间LS i-j
LS i-j＝LF i-j－D i-j
--在不影响计划工期的前提下，该工作最迟必须开始的时刻。

（五）工作的总时差TF i-j
TF i-j＝LS i-j－ES i-j 或TF i-j＝LF i-j－EF i-j
--在不影响计划工期的前提下，该工作存在的机动时间。

（六）自由时差FF i-j
FF i-j＝ES j-k－EF i-j
--在不影响紧后工作最早开始时间的前提下，该工作存在的机动时间。

作业1：根据表中逻辑关系，绘制双代号网络图。