第三章_动力学方程的三种基本形式
- 格式:ppt
- 大小:11.17 MB
- 文档页数:45




动力学方程1. 引言动力学方程是研究物体在运动中受到的力学作用的数学描述。
它是物理学中非常重要的概念,广泛应用于各个领域,包括经济学、工程学、生物学等。
本文将介绍动力学方程的基本概念、求解方法以及应用等方面的内容。
2. 动力学方程的定义动力学方程描述了物体在运动过程中所受到的力学作用。
一般来说,动力学方程可以分为牛顿第二定律和拉格朗日方程两种形式。
2.1 牛顿第二定律牛顿第二定律是描述质点运动的基本定律之一。
它的数学表达式为:F = ma其中,F表示物体所受的合力,m表示物体的质量,a表示物体的加速度。
根据牛顿第二定律,我们可以得到物体在受到外力作用下的运动方程。
2.2 拉格朗日方程拉格朗日方程是描述物体运动的另一种形式,它基于能量守恒的原理。
拉格朗日方程的数学表达式为:d/dt ( ∂L/∂(dq/dt) ) - ∂L/∂q = 0其中,L表示物体的拉格朗日函数,q表示广义坐标,t表示时间。
拉格朗日方程可以从运动的作用量原理推导得到,它可以描述多自由度、非洛加多力学系统的运动。
3. 动力学方程的求解方法求解动力学方程是研究物体运动的关键步骤之一。
常见的求解方法主要有解析解法和数值解法两种。
3.1 解析解法解析解法是通过数学计算的方法,求得动力学方程的精确解。
在一些简单的情况下,动力学方程可以直接求解得到解析解。
例如,简谐振动的运动方程可以通过解微分方程得到解析解。
3.2 数值解法数值解法是通过数值计算的方法,求得动力学方程的近似解。
数值解法通常采用数值求解微分方程的方法,例如欧拉法、龙格-库塔法等。
数值解法在复杂的情况下具有更好的适用性,但是精度相对较低。
4. 动力学方程的应用动力学方程广泛应用于各个领域,下面将简要介绍一些典型的应用。
4.1 经济学在经济学中,动力学方程可以用于描述经济系统的运动规律。
例如,经济增长模型可以通过动力学方程来描述经济发展的速度和方向,从而为经济政策制定提供理论依据。

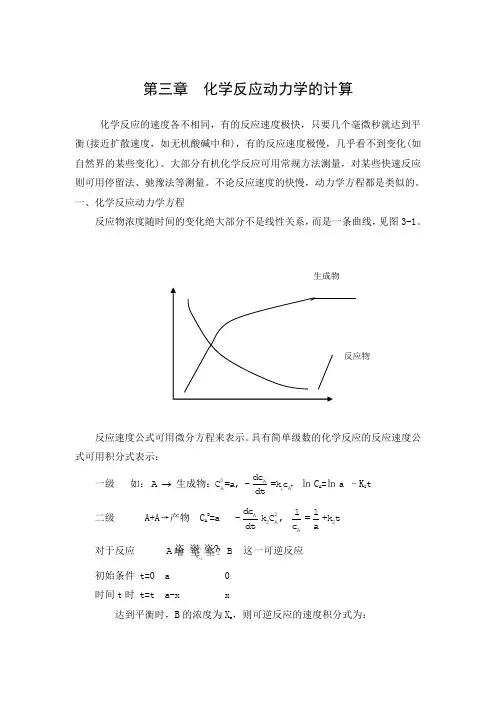
第三章 化学反应动力学的计算化学反应的速度各不相同,有的反应速度极快,只要几个毫微秒就达到平衡(接近扩散速度,如无机酸碱中和),有的反应速度极慢,几乎看不到变化(如自然界的某些变化)。
大部分有机化学反应可用常规方法测量,对某些快速反应则可用停留法、驰豫法等测量。
不论反应速度的快慢,动力学方程都是类似的。
一、化学反应动力学方程反应物浓度随时间的变化绝大部分不是线性关系,而是一条曲线,见图3-1。
反应速度公式可用微分方程来表示。
具有简单级数的化学反应的反应速度公式可用积分式表示:一级 如:0AA1Adc A C =a, -=k c dt 生成物:,㏑C A =㏑a –K 1t 二级 A+A →产物 C A 0=a 2A 2A 2A d c 11-k C , =+k t d t c a对于反应 1-1k k A B 这一可逆反应初始条件 t=0 a 0 时间t 时 t=t a-x x达到平衡时,B 的浓度为X e ,则可逆反应的速度积分式为: 级数:1-1 1-10k A A e e 1A -1B k 0e 0C =a dc x xA B=-k C +k C : =kt dt a x -xC =0ln 1-21-10Ak0A e e e B 1A -1B C k e e 0CC =a dc x ax +x(a-x )A B+C C =0=-k C +k C C : =kt dt 2a-x a(x -x)C =0ln 二、常微分方程的解化学反应动力学方程是用微分方程表示的,对于简单的反应,可直接求得微分方程的解。
微分方程:()(1)(,,,......)......(1)n n y f x y y y -'=在区间a<x<b 的解,是指()y x ϕ=,这样一个函数,在所述区间内存在导数()(),(),......()n x x x ϕϕϕ'''。
且对于区间a<x<b 内的每一个x ,等式(1)都成立。


Chapter 3 流体动力学基本方程例如求解定常均匀来流绕流桥墩时的桥墩受力问题:流场和桥墩表面受力由(边界条件+控制方程组)决定。
本章任务建立控制方程组,确定边界条件的近似描述和数学表达。
I 质量连续性方程(质量守恒方程) I-1方程的导出物质体(或系统)的质量恒定不变——质量守恒假设。
质量守恒假设对于很多流动问题是良好近似,分子热运动引起的系统与外界的物质交换可忽略不计。
在此假设下,对物质体τ有0dd dtτρτ=⎰。
根据输运定理,设t 时刻该系统所占控制体为CV ,对应控制面CS ,则有0CVCSd v ds tρτρ∂+⋅=∂⎰⎰⎰——质量守恒方程积分形式。
上式亦表明,CV 内单位时间内的质量减少=CS 上的质量通量。
由奥高公式得()CSCVv ds v d ρρτ⋅=∇⋅⎰⎰⎰,于是有()0CV v d t ρρτ∂⎡⎤+∇⋅=⎢⎥∂⎣⎦⎰。
考虑到τ的任意性,故有()0v t ρρ∂+∇⋅=∂,即 0d v dtρρ+∇⋅= ——质量守恒方程微分形式 I-2各项意义分析: 1)dt d ρ——流体微团密度随时间的变化率;定常流动0=∂∂t ρ;不可压缩流动0=dt d ρ;均质流体的不可压缩流动.const ρ=。
2)由0=dtmd δ(m δ为微团的质量)知11d d dt dt ρδτρδτ=-(δτ为该微团t 时刻体积),从而知v ∇⋅=流体微团体积随时间的相对变化率,即体膨胀率。
3)不可压缩流体0d dtρ=,故有 0v ∇⋅=。
由奥高公式有CVCSv ds vd τ⋅=∇⋅⎰⎰⎰,可见对于不可压缩流动,任意闭合曲面上有0CSv ds ⋅=⎰⎰。
不可压缩流动满足的0v ∇⋅=或0CSv ds ⋅=⎰⎰是对速度场的一个约束。
例1、1)定常流场中取一段流管,则由0CSv ds ⋅=⎰⎰易知:222111S V S V ρρ=;如为均质不可压缩流动,则1122V S V S =。


量子力学中的动力学方程量子力学是描述微观粒子行为的理论框架,其核心是动力学方程。
动力学方程描述了体系在时间演化中的规律,而量子力学的动力学方程则基于薛定谔方程和海森堡方程。
本文将探讨量子力学中的动力学方程及其应用。
1. 薛定谔方程薛定谔方程是量子力学中最重要的动力学方程之一,它描述了量子体系的时间演化。
薛定谔方程的一般形式为:iℏ∂Ψ/∂t = HΨ其中,i是虚数单位,ℏ是约化普朗克常数,Ψ是波函数,H是哈密顿算符。
薛定谔方程说明了波函数随时间的演化符合线性定律。
2. 海森堡方程与薛定谔方程不同,海森堡方程是描述量子体系的运动方程,它不涉及波函数。
海森堡方程的一般形式为:dA/dt = (1/iℏ) [A, H]其中,A是动力学变量的算符,H是哈密顿算符。
海森堡方程描述了算符随时间的演化。
3. 动力学方程的应用薛定谔方程和海森堡方程是量子力学中重要的基本方程,它们在各个领域的研究中被广泛应用。
3.1. 原子物理学在原子物理学中,动力学方程用于描述原子的能级结构和电子的行为。
通过求解薛定谔方程,可以得到原子的能级和波函数分布,进而理解光谱现象和原子之间的相互作用。
3.2. 凝聚态物理学在凝聚态物理学中,动力学方程被用于研究固体材料的电子结构和宏观性质。
通过薛定谔方程的数值解和近似方法,可以计算出电子的能带结构、磁性行为以及导电性等重要物理性质。
3.3. 量子计算与量子信息动力学方程在量子计算和量子信息领域起着关键作用。
通过研究量子系统的时间演化,可以实现量子计算中的逻辑操作和量子通信中的量子态传输。
4. 小结量子力学中的动力学方程,即薛定谔方程和海森堡方程,是描述量子体系时间演化的基本工具。
这些方程在原子物理学、凝聚态物理学以及量子计算与量子信息等领域中有着广泛的应用。
通过研究动力学方程,我们可以深入了解微观世界的规律,为实验验证和技术应用提供理论基础。
简而言之,“量子力学中的动力学方程”是研究量子体系时间演化的核心内容,薛定谔方程和海森堡方程是具体的数学表达式,它们在各个物理学领域中扮演着重要的角色。

物理学中的动力学方程动力学方程是物理学中非常重要的一个概念,因为它描述了物质在空间中的运动规律。
动力学方程运用了牛顿力学和微积分理论,用一种特殊的形式表达了物体受到的所有力的总和,从而描述了物体的运动。
牛顿第二定律和简单的机械系统牛顿第二定律是描述力和加速度之间关系的经典方程,它基于牛顿的三大定律。
根据牛顿第二定律,物体的加速度与物体所受合外力的大小成正比,与物体的质量成反比。
这个定律常常被写成如下的形式:F = ma其中,F代表受力的大小,m代表物体的质量,a代表物体的加速度。
这个公式非常基础,但它可以描述许多力学问题。
例如,如果有一个简单的弹簧振子,振子受到弹簧的拉力以及阻尼力的作用,则可以使用牛顿第二定律来描述振子的运动。
在这个情况下,弹簧拉力和阻尼力构成了振子所受的合外力,而振子运动的加速度可以用振幅和周期来确定。
非完整约束和拉格朗日力学但有些问题不那么简单。
例如,对于两个相互作用的物体,它们之间的力可能是垂直于它们之间的距离的,因此无法直接使用牛顿第二定律描述它们的运动。
这种约束被称为非完整约束。
拉格朗日力学则是一种针对非完整约束的运动方程描述方法。
它不依赖于特定的坐标系,而是将所有描述运动的坐标都视为等价的。
拉格朗日力学的关键是拉格朗日方程,也被称为运动方程。
它基于运动的的能量和拉格朗日函数,表示出了物体的运动性质。
拉格朗日方程的形式如下:L = T - V其中,T代表物体的动能,V代表物体所受的势能。
拉格朗日方程根据最小作用原理,描述了物体从初始状态到结束状态的运动轨迹。
这个方法被广泛应用于各种物理问题的求解中。
哈密顿力学和正则变量哈密顿力学是拉格朗日力学的另一种形式。
它基于哈密顿函数,而不是拉格朗日函数。
哈密顿函数表示物体的动量和能量之和。
哈密顿函数的形式如下:H = T + V其中,T代表物体的动能,V代表物体所受的势能。
哈密顿力学使用正则变量来描述系统的运动。
正则变量与系统的状态量形成了一种变换关系,使得能量和动量之间的关系更加清晰。
动力学方程与运动解析动力学方程是研究物体运动的一种重要工具,它描述了物体在运动过程中所受到的力和加速度之间的关系。
通过解析动力学方程,我们可以深入理解物体的运动规律和特性。
一、动力学方程的基本概念动力学方程是基于牛顿第二定律而建立的,它表达了物体的质量乘以加速度等于物体所受的合力。
这个方程可以用数学形式表示为:F = ma,其中F表示物体所受的合力,m表示物体的质量,a表示物体的加速度。
二、解析动力学方程的方法解析动力学方程的方法有很多种,下面我们来介绍一些常见的方法。
1. 分离变量法对于一些简单的动力学方程,我们可以通过分离变量的方法来求解。
首先将方程中的变量分离到等式两边,然后进行积分,最后得到解析解。
这种方法适用于一些具有特殊形式的动力学方程。
2. 变量替换法有时候,我们可以通过引入新的变量来简化动力学方程的求解过程。
通过合适的变量替换,可以将原方程转化为更简单的形式,从而更容易求解。
3. 迭代法对于一些复杂的动力学方程,我们可以采用迭代的方法来逼近解析解。
迭代法的基本思想是通过不断迭代,逐步逼近真实解。
这种方法虽然计算量较大,但可以得到较为精确的解析解。
三、动力学方程的应用动力学方程在物理学、工程学等领域有着广泛的应用。
下面我们来介绍一些典型的应用场景。
1. 自由落体运动自由落体是指物体在无外力作用下自由下落的运动。
通过解析动力学方程,我们可以推导出自由落体运动的加速度等于重力加速度,并得到物体的位置、速度与时间的关系。
这对于研究物体在重力场中的运动规律非常重要。
2. 弹性碰撞弹性碰撞是指两个物体在碰撞过程中能量守恒且动量守恒的碰撞。
通过解析动力学方程,我们可以推导出碰撞前后物体的速度和动量之间的关系,从而研究碰撞过程中的能量转化和物体的运动轨迹。
3. 摆动运动摆动运动是指物体在重力作用下以一定频率来回摆动的运动。
通过解析动力学方程,我们可以推导出摆动运动的周期和频率与摆长、重力加速度之间的关系,从而研究摆动运动的特性和规律。
第三章流体动力学基础本章是流体动力学的基础。
主要阐述了流体运动的两种描述方法,运动流体的基本类别与基本概念,用欧拉法解决运动流体的连续性微分方程、欧拉运动微分方程及N-S方程。
此外,还阐述了无旋流与有旋流的判别,引出了流函数与势函数的概念,并且说明利用流网与势流叠加原理可解决流体的诸多复杂问题。
第一节流体流动的基本概念1.流线(1)流线的定义流线(stream line)是表示某一瞬时流体各点流动趋势的曲线,曲线上任一点的切线方向与该点的流速方向重合。
图3-1为流线谱中显示的流线形状。
(2)流线的作法:在流场中任取一点(如图3-2),绘出某时刻通过该点的流体质点的流速矢量u1,再画出距1点很近的2点在同一时刻通过该处的流体质点的流速矢量u2…,如此继续下去,得一折线1234 …,若各点无限接近,其极限就是某时刻的流线。
流线是欧拉法分析流动的重要概念。
图3-1 图3-2(3)流线的性质(图3-3)a.同一时刻的不同流线,不能相交。
图3-3因为根据流线定义,在交点的液体质点的流速向量应同时与这两条流线相切,即一个质点不可能同时有两个速度向量。
b.流线不能是折线,而是一条光滑的曲线。
因为流体是连续介质,各运动要素是空间的连续函数。
c.流线簇的疏密反映了速度的大小(流线密集的地方流速大,稀疏的地方流速小)。
因为对不可压缩流体,元流的流速与其过水断面面积成反比。
(4)流线的方程(图3-4)根据流线的定义,可以求得流线的微分方程:图3-4设d s为流线上A处的一微元弧长:u为流体质点在A点的流速:因为流速向量与流线相切,即没有垂直于流线的流速分量,u和d s重合。
所以即展开后得到:——流线方程(3-1)(或用它们余弦相等推得)2.迹线(1)迹线的定义迹线(path line)某一质点在某一时段内的运动轨迹线。
图3-5中烟火的轨迹为迹线。
(2)迹线的微分方程(3-2)式中,u x,u y,u z均为时空t,x,y,z的函数,且t是自变量。
空气动力学方程包括三个基本方程,分别是连续性方程、动量方程和能量方程。
这些方程描述了空气在流动过程中的特性。
连续性方程:这是描述质量守恒的方程。
在不可压缩流动的假设下,它在形式上表现为流体在管道不同截面处流量相同的假设。
这个方程的形式是:
ρ1 * V1 = ρ2 * V2
其中,ρ是密度,V是速度,1和2分别表示不同的截面。
动量方程:这是描述动量守恒的方程。
它的形式是:
ρ* (dV/dt) = -∇* (μ* ∇V) + τ
其中,ρ是密度,dV/dt是速度的变化率,∇是拉普拉斯算子,μ是动力粘度,∇V是速度梯度,τ是表面张力项。
能量方程:这是描述能量守恒的方程。
它的形式是:
ρ* (d(ρE)/dt) = -∇* (ρq) + ∇* (μ* ∇V) + ∂(σ/∂t)
其中,ρE是包含密度和内能的变量,ρq是包含密度和总能量的变量,μ是动力粘度,∇V是速度梯度,σ是表面张力项。
这些方程都是在控制体和流体微团两种模型下推导出来的。
控制体是在空间中取一个有限的封闭容积,基本原理应用于控制体内的流体和跨过控制体表面的流体。
流体微团是在流体中取一无限小的流体元素,研究基本原理在其上的作用。