第七章动力学的基本方程

动力学方程1. 引言动力学方程是研究物体在运动中受到的力学作用的数学描述。

它是物理学中非常重要的概念，广泛应用于各个领域，包括经济学、工程学、生物学等。

本文将介绍动力学方程的基本概念、求解方法以及应用等方面的内容。

2. 动力学方程的定义动力学方程描述了物体在运动过程中所受到的力学作用。

一般来说，动力学方程可以分为牛顿第二定律和拉格朗日方程两种形式。

2.1 牛顿第二定律牛顿第二定律是描述质点运动的基本定律之一。

它的数学表达式为：F = ma其中，F表示物体所受的合力，m表示物体的质量，a表示物体的加速度。

根据牛顿第二定律，我们可以得到物体在受到外力作用下的运动方程。

2.2 拉格朗日方程拉格朗日方程是描述物体运动的另一种形式，它基于能量守恒的原理。

拉格朗日方程的数学表达式为：d/dt ( ∂L/∂(dq/dt) ) - ∂L/∂q = 0其中，L表示物体的拉格朗日函数，q表示广义坐标，t表示时间。

拉格朗日方程可以从运动的作用量原理推导得到，它可以描述多自由度、非洛加多力学系统的运动。

3. 动力学方程的求解方法求解动力学方程是研究物体运动的关键步骤之一。

常见的求解方法主要有解析解法和数值解法两种。

3.1 解析解法解析解法是通过数学计算的方法，求得动力学方程的精确解。

在一些简单的情况下，动力学方程可以直接求解得到解析解。

例如，简谐振动的运动方程可以通过解微分方程得到解析解。

3.2 数值解法数值解法是通过数值计算的方法，求得动力学方程的近似解。

数值解法通常采用数值求解微分方程的方法，例如欧拉法、龙格-库塔法等。

数值解法在复杂的情况下具有更好的适用性，但是精度相对较低。

4. 动力学方程的应用动力学方程广泛应用于各个领域，下面将简要介绍一些典型的应用。

4.1 经济学在经济学中，动力学方程可以用于描述经济系统的运动规律。

例如，经济增长模型可以通过动力学方程来描述经济发展的速度和方向，从而为经济政策制定提供理论依据。

第七章动力学1．化学反应速率对定容条件下的化学反应aA + dD →gG + hH化学反应速率2．化学反应速率方程（动力学方程）：对基元反应: a A + b B + ··· ···→产物质量作用定律a +b + ··· ------反应级数零级反应r=k ，k的量纲为mol.L-1.s-1一级反应r=kc，k的量纲为s-1；二级反应r=kc2 ，k的量纲为(mol·L -1)-1 ·s-13.经验速率方程复合反应a A + b B + ··· ···→产物经验速率方程k ---- 速率常数；有量纲。

nA、nB。

----- A物质、B物质的分级数。

n = nA + nB + ···----- 反应级数；4．简单级数反应的特征（重要）5. van’t Hoff 温度每升高10℃，反应速率大约增加2～4倍=2~4Arrhenius经验公式（1）. 微分形式（2）. 不定积分形式（3）. 定积分形式（4）. 指数形式C --- 积分常数 T ：KR = 8.314 J / K·mol E a ---- 活化能 (J / mol) ;A--- 指前因子或频率因子（与k 的单位相同） 6．--- 活化分子的平均能量；--- 反应物分子的平均能量; J / mol --- 1mol 具有平均能量的分子变成活化分子所需要的最低能量; J / mol复合反应及近似处理（作参考，会自己推导）一．对峙反应（可逆反应） 1-1级反应达平衡时A 、B 的平衡浓度：二．平行反应A 物质消耗的总反应速率为： 积分得：三．连串反应 反应四． 链反应。

*E rE a E。

第七章不可压缩流体动力学基础在询面的章节中，我们学习了理想流体和粘性流体的流动分析，按照水力学的 观点，求得平均量。

但是，很多问题需要求得更加详细的信息，如流速、压强等 流动参数在二个或三个坐标轴方向上的分布情况。

本章的容介绍流体运动的基本 规律、基本方程、定解条件和解决流体问题的基本方法。

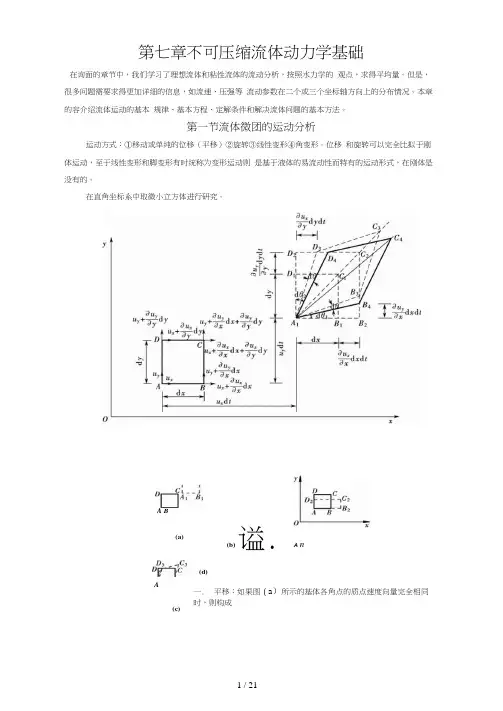
第一节流体微团的运动分析运动方式：①移动或单纯的位移（平移）②旋转③线性变形④角变形。

位移 和旋转可以完全比拟于刚体运动，至于线性变形和脚变形有时统称为变形运动则 是基于液体的易流动性而特有的运动形式，在刚体是没有的。

在直角坐标系中取微小立方体进行研究。

(b)谥.A n(d)一. 平移：如果图（a ）所示的基体各角点的质点速度向量完全相同时，则构成(c)A B(a)A了液体基体的单纯位移，其移动速度为心、®、“,。

基体在运动中可能沿直线也 可能沿曲线运动，但其方位与形状都和原来一样（立方基体各边的长度保持不 变）。

二、 线变形：从图（b ）中可以看出，由于沿y 轴的速度分量，B 点和C 点都比 A 点和D 点大了竺如 而比就代表〃y = l 时液体基体运动时，在单位时间沿勿dyy 轴方向的伸长率。

du x °"、. du : dxdydz三、 角变形（角变形速度）—BIA ■ dp -------------------------------- Jda-0 = dp + 00 =J"些+些k dz. dx四、旋转（旋转角速度）1O = —0 =—21勿du vdx—dx角变形:血 A那么，代入欧拉加速度表达式，得：du r du Tdu r八 八5=说=古叫 云+"卑+"0+-叭巴加、6仇 du Ya v = ----- = — + u v ---------- + U.0, +ii t a ）. -iLCoydt dt dy “'2 …加.du diL q 。

动力学方程的推导和解析动力学方程是研究物体运动规律的重要工具，在物理学和工程学等领域有着广泛的应用。

本文将从基本概念出发，介绍动力学方程的推导和解析方法，以帮助读者更好地理解和应用这一重要的物理学原理。

一、动力学方程的基本概念动力学方程描述了物体运动的规律，它是牛顿力学的基石。

在牛顿力学中，动力学方程可以用力的平衡原理来推导，即物体所受合力等于物体的质量乘以加速度。

这一原理可以表示为以下形式的方程：F = ma其中，F代表物体所受的合力，m代表物体的质量，a代表物体的加速度。

这个方程是动力学方程的基本形式，可以用来描述物体在给定力作用下的运动状态。

二、动力学方程的推导动力学方程的推导可以通过分析物体所受的力和质量之间的关系来实现。

首先，我们需要确定物体所受的力，这些力可以来自于重力、弹力、摩擦力等。

然后，根据力的平衡原理，将这些力相加得到物体所受的合力。

最后，将合力除以物体的质量，得到物体的加速度。

以一个简单的例子来说明动力学方程的推导过程。

假设有一个质量为m的物体，受到一个向下的重力作用，以及一个向上的弹力。

根据牛顿第二定律，物体所受的合力等于物体的质量乘以加速度。

因此，我们可以得到以下方程：mg - kx = ma其中，g代表重力加速度，k代表弹簧的劲度系数，x代表弹簧的伸长量。

这个方程描述了物体在重力和弹力作用下的运动规律。

三、动力学方程的解析解析动力学方程是指通过数学方法求解方程，得到物体在给定力作用下的运动规律。

一般情况下，动力学方程是一个微分方程，需要通过积分或其他数学方法来求解。

继续以前面的例子为基础，我们可以通过求解微分方程来得到物体的运动规律。

首先，将方程重写为标准形式：ma + kx = mg然后，我们可以使用数学方法来求解这个微分方程。

例如，我们可以假设物体的位移x是一个关于时间t的函数，即x = x(t)，然后将这个函数代入微分方程中，得到一个关于x和t的方程。

通过求解这个方程，我们可以得到物体的位移随时间变化的函数关系。

第七章 粘性流体动力学基础实际流体都具有粘性，而在研究粘性较小的流体的某些流动现象时，可将有粘性的实际流体近似地按无粘性的理想流体处理。

例如，粘性小的流体在大雷诺数情况下，其流速和压强分布等均与理想流体理论十分接近。

但在研究粘性小的流体的另一些问题时，与实际情况不符，如按照理想流体理论得到绕流物体的阻力为零。

产生矛盾的主要原因是未考虑实际流体所具有的粘性对流动的影响。

本章，首先建立具有粘性的实际流体运动微分方程，并介绍该方程的在特定条件下的求解。

由于固体边界对流体与固体的相互作用有重要的影响，本章后面主要介绍边界层的一些基本概念、基本原理和基本的分析方法。

§7.1 纳维—斯托克斯方程7.1.1 粘性流体的应力实际流体具有粘性，运动时会产生切应力，它的力学性质不同于理想流体，在作用面上的表面应力既有压应力，也有切应力。

在流场中任取一点M ，过该点作一垂直于z 轴的水平面，如图7-1 所示。

过M 点作用于水平面上的表面应力p n 在x 、y 、z 轴上的分量为一个垂直于水平面的压应力p zz 和两个与水平面相切的切应力τzx 、τzy 。

压应力和切应力的下标中第一个字母表示作用面的法线方向，第二个字母表示应力的作用方向。

显然，通过M 点在三个相互垂直的作用面上的表面应力共有九个分量，其中三个是压应力p xx 、p yy 、p zz ，六个是切应力τxy 、τxz 、τyx 、τyz 、τzx 、τzy ，将应力分量写成矩阵形式：图7-1 作用于水平面的表面应力⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧ττττττzz zyzxyz yy yxxz xy xx p p p (7-1) 九个应力分量中，由于τxy =τyx 、τyz =τzy 、τzx =τxz ，粘性流体中任意一点的应力分量只有6个独立分量，即τxy 、τyz 、τzx 、p xx 、p yy 、p zz 。

7.1.2 应力形式的运动方程在粘性流体的流场中，取一以点M 为中心的微元直角六面体，其边长分别为dx 、dy 、 dz 。

动力学方程简介动力学方程是描述物体或系统运动的数学表达式。

它基于牛顿第二定律，即力等于质量乘以加速度。

动力学方程在物理学、工程学、生物学等领域起着重要作用，可以用来研究运动的特性以及对系统的控制。

动力学方程的基本概念动力学方程由一组微分方程组成，描述了物体或系统随着时间的变化而发生的运动。

一般来说，动力学方程的形式为:m*a = ΣF其中，m表示物体的质量，a表示物体的加速度，ΣF表示作用在物体上的力的合力。

动力学方程的推导根据牛顿第二定律，物体的加速度与作用在物体上的力成正比。

根据这个基本原理，我们可以推导出物体的动力学方程。

首先，我们考虑一个简单的情况：只有一个力作用在物体上。

假设这个力的大小为F，方向与物体的加速度相同。

根据牛顿第二定律，我们可以得到: m*a = F这就是物体的动力学方程。

这个方程可以描述物体的运动情况。

当有多个力作用在物体上时，我们需要将所有力的大小和方向都考虑进去。

我们可以将所有力的合力表示为ΣF。

这样，物体的动力学方程可以表示为:m*a = ΣF这个方程可以描述物体在多个力作用下的运动情况。

动力学方程包括了物体的质量、加速度以及力的合力。

动力学方程的应用举例自由落体自由落体是动力学方程的一个重要应用。

假设一个物体在重力作用下自由下落。

根据牛顿第二定律，我们可以得到:m*a = m*g其中，m是物体的质量，g是重力加速度。

这个方程描述了物体在自由落体过程中的运动情况。

弹簧振子弹簧振子也是动力学方程的一个典型应用。

考虑一个质点通过弹簧与固定点相连，质点的运动受到弹簧的弹力作用。

假设质点的质量为m，弹簧的劲度系数为k，质点的位移为x，我们可以得到动力学方程:m*a = -k*x这个方程描述了弹簧振子在弹力作用下的运动情况。

当质点受到弹力作用时，它的加速度与位移成反比关系。

结论动力学方程是描述物体或系统运动的数学表达式，它基于牛顿第二定律。

动力学方程可以用来研究运动的特性以及对系统的控制。

第十一章 化学动力学§化学反应的反应速率及速率方程1.反应速率的定义非依时计量学反应: 若某反应不存在中间物，或虽有中间物，但其浓度甚微可忽略不计，则此类反应将在整个反应过程中符合一定的计量式。

那么，这类反应就称为非依时计量学反应 某反应的化学计量式：B B0B ν=∑对非依时计量学反应，反应进度ξ定义为：B B d d /n ξν=转化速率为：B B d /d (1/)(d /d )t n t ξξν==& 反应速率为：B B /(1/)(d /d )r V V n t ξν==& 即用单位时间单位体积内化学反应的反应进度来定义反应速率。

对非依时计量学反应，此定义与用来表示速率的物质B 的选择无关，与化学计量式的写法有关。

对于恒容反应，反应速率可表示为：B B (1/)(d /d )r c t ν= 对任何反应： E F G H e f g h +=+G E F Hd d d d 1111d d d d c c c c re tf tg th t=-=-==2.基元反应 定义：如果一个化学反应，反应物分子在碰撞中相互作用直接转化为生成物分子，这种反应称为基元反应。

基元反应为组成一切化学反应的基本单元。

例如：2222C +M =2C +M C +H =HC +H H +C =HC +C 2C +M =C +Mg g化学反应方程，除非特别注明，一般都属于化学计量方程，而不代表基元反应。

反应机理：反应机理又称为反应历程。

在总反应中，连续或同时发生的所有基元反应称为反应机理，在有些情况下，反应机理还要给出所经历的每一步的立体化学结构图。

3. 基元反应的速率方程--质量作用定律、反应分子数（1）反应分子数：基元反应方程式中各反应物分子个数之和，称为反应分子数。

（2）质量作用定律：对于基元反应，反应速率与反应物浓度的幂乘积成正比。

幂指数就是基元反应方程中各反应物的系数。

这就是质量作用定律，它只适用于基元反应。