九年级数学下册2.2.2第1课时圆周角定理与推论1试题(新版)湘教版

２0１7春九年级数学下册2.2.2 圆周角第1课时圆周角定理及其推论1学案(新版)湘教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方，但是任然希望（2０１７春九年级数学下册2.２.2 圆周角第1课时圆周角定理及其推论1学案(新版)湘教版)的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步，以下为20１7春九年级数学下册 2.2．2 圆周角第1课时圆周角定理及其推论１学案(新版）湘教版的全部内容。

第1课时圆周角定理及其推论１1．理解圆周角的概念,学会识别圆周角;2.在实际操作中探索圆的性质,了解圆周角与圆心角的关系,并能应用其进行简单的计算与证明;3.在探索过程中,体会观察、猜想的思维方法,在定理的证明过程中,体会化归和分类讨论的数学思想和归纳的方法.自学指导阅读课本P49~52,完成下列问题.知识探究1.顶点在圆上,角的两边都与圆相交的角叫作圆周角．２.圆周角的度数等于它所对弧上的圆心角度数的一半．3．在同圆（或等圆)中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等．自学反馈１。

如图所示，点A、Ｂ、C在圆周上,∠A＝65°，求∠D的度数.解:65°．2.如图所示,已知圆心角∠BOC=１０0°,点Ａ为优弧错误!上一点,求圆周角∠BAC的度数。

解：50°。

3。

如图所示,在⊙O中，∠AOB=100°,C为优弧错误!的中点，求∠CAＢ的度数．解：６５°。

活动1 小组讨论例１下列图形中的角是圆周角的是（Ｂ)例２如图，AB是⊙O的直径，Ｃ,Ｄ为圆上两点，∠AＯC＝130°,则∠Ｄ等于（A )A.25°Ｂ.30°C.35°Ｄ.５0°例3 如图，在⊙O中，错误!＝错误!，∠AOB＝５０°,则∠ADC的度数是( D ）A.5０°B.4０°C.30°D.25°本题考查的是圆周角定理,熟知在同圆或等圆中，同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键．活动2 跟踪训练1.如图，锐角△ABC的顶点Ａ，B,C均在⊙O上，∠ＯAC=２0°,求∠B的度数.解:∵ＯA=OC,∠OAＣ=20°，∴∠ＯＣA=∠OAC＝２0°.∴∠AＯC=180°—２∠OCA＝180°-2×2０°＝１40°．1∠AＯC＝70°．∴∠Ｂ=22。

第1课时圆周角定理及其推论11．理解圆周角的概念,学会识别圆周角；2．在实际操作中探索圆的性质，了解圆周角与圆心角的关系，并能应用其进行简单的计算与证明；3．在探索过程中,体会观察、猜想的思维方法,在定理的证明过程中，体会化归和分类讨论的数学思想和归纳的方法．自学指导阅读课本P49～52，完成下列问题.知识探究1．顶点在圆上，角的两边都与圆相交的角叫作圆周角．2．圆周角的度数等于它所对弧上的圆心角度数的一半．3．在同圆(或等圆)中,同弧或等弧所对的圆周角相等，相等的圆周角所对的弧也相等．自学反馈1。

如图所示，点A、B、C在圆周上，∠A=65°,求∠D的度数.解：65°.2.如图所示，已知圆心角∠BOC=100°，点A为优弧错误!上一点,求圆周角∠BAC的度数。

解：50°。

3。

如图所示，在⊙O中，∠AOB=100°,C为优弧错误!的中点,求∠CAB的度数.解：65°。

活动1 小组讨论例1下列图形中的角是圆周角的是（ B ）例2 如图，AB是⊙O的直径,C，D为圆上两点，∠AOC＝130°,则∠D等于( A )A．25° B．30°C．35° D．50°例3 如图，在⊙O中,错误!＝错误!，∠AOB＝50°,则∠ADC的度数是( D )A．50° B．40°C．30° D．25°本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．活动2 跟踪训练1.如图，锐角△ABC的顶点A,B,C均在⊙O上，∠OAC=20°，求∠B的度数．解:∵OA=OC ，∠OAC=20°，∴∠OCA=∠OAC=20°．∴∠AOC =180°—2∠OCA=180°-2×20°=140°．∴∠B=21∠AOC=70°． 2。

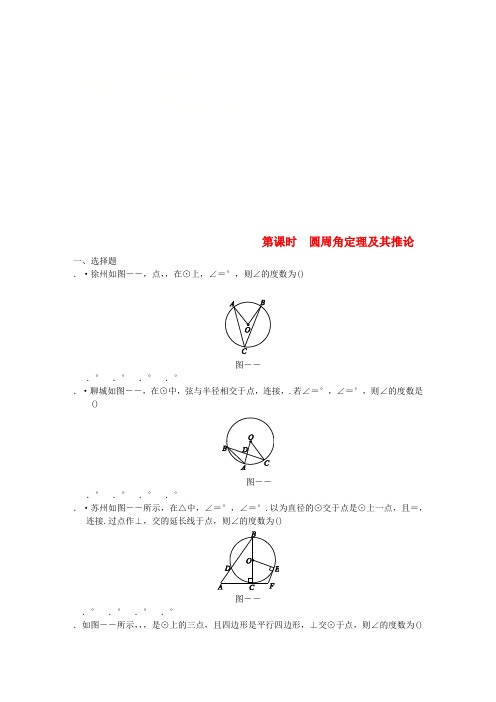
第课时圆周角定理及其推论一、选择题．·徐州如图－－，点，，在⊙上，∠＝°，则∠的度数为()图－－．° ．°．°．°．·聊城如图－－，在⊙中，弦与半径相交于点，连接，.若∠＝°，∠＝°，则∠的度数是()图－－．°．°．°．°．·苏州如图－－所示，在△中，∠＝°，∠＝°.以为直径的⊙交于点是⊙上一点，且＝，连接.过点作⊥，交的延长线于点，则∠的度数为()图－－．°．°．°．°．如图－－所示，，，是⊙上的三点，且四边形是平行四边形，⊥交⊙于点，则∠的度数为()图－－．°．°．°．°二、填空题．如图－－，弦，相交于点，连接，，在不添加辅助线的情况下，请在图中找出一对相等的角，它们是．图－－．如图－－，在⊙中，＝，∠＝°，则∠＝°.图－－．如图－－所示，点在⊙上，将圆心角∠绕点按逆时针方向旋转到∠′′，若∠＝°，∠′＝°，则∠′＝°.图－－．如图－－，经过原点的⊙与轴、轴分别交于点，，是劣弧上一点，∠＝°，则∠＝°，∠＝°.图－－．如图－－，在⊙中，弦＝，是圆上一点，且∠＝°，则⊙的半径＝．图－－三、解答题．如图－－，点，和都在⊙上，且∥，∥.()求证：四边形为菱形；()求∠的度数．图－－．如图－－，点，，在⊙上，弦平分∠交于点.求证：＝·.图－－．·长沙模拟如图－－，是⊙的一条弦，，是⊙上的两个动点，且在弦的异侧，连接.()已知＝，平分∠，求证：＝；()若∠＝°，⊙的半径为，求四边形的面积的最大值．图－－．如图－－，⊙是△的外接圆，是的中点，∥交的延长线于点，若＝，∠＝°，求的长．图－－素养提升新定义·探索性问题如图－－，为圆外一点，交⊙于点，，交⊙于点，，的度数为°，的度数为°.()求∠的度数；()如果我们把顶点在圆外，并且两边都和圆相交的角叫圆外角，请你仿照圆周角定理“圆周角的度数等于它所对弧的度数的一半”来概括出圆外角的性质；()请你定义“圆内角”，并概括圆内角的性质．图－－．．[解析] ∵∠＝°，∠＝°，∴∠＝∠－∠＝°－°＝°，∴∠＝∠＝×°＝°，∴∠＝∠－∠＝°－°＝°.．[解析] ∵∠＝°，∠＝°，∴∠＝°.∵＝，∴∠＝∠＝°.又∵∠＝∠＝°，∴∠＝°－°－°－°＝°.．[解析] 连接.∵四边形是平行四边形，∴＝.又∵＝＝，∴＝＝，∴△为等边三角形. ∵⊥，∥，∴⊥，∴∠＝∠＝°，由圆周角定理，得∠＝∠＝°.．本题答案不唯一，如∠＝∠．[答案][解析] ∵＝，∴＝，∴∠＝∠.又∵∠＝°，∴∠＝°.．[答案][解析] ∵∠′＝°，∴∠′＝∠′＝°.∵将圆心角∠绕点按逆时针方向旋转到∠′′，∴∠′′＝∠＝°，∴∠′＝∠′＋∠′′＝°.．．[答案][解析] ∵∠＝°，∴∠＝°.∵＝＝，∴＋＝( )，解得＝，故答案为.．解：()证明：∵∥，∥，∴四边形为平行四边形．又∵＝，∴四边形为菱形．()如图，连接.∵四边形为菱形，＝，∴△为等边三角形，∴∠＝°，同理∠＝°，∴∠＝°.．[解析] 欲证＝·，只需证＝，则只需证△∽△.由于平分∠，则∠＝∠.因为∠＝∠，所以∠＝∠.又由于∠为公共角，命题可证．证明：∵平分∠，∴∠＝∠.又∵∠＝∠，∴∠＝∠.又∵∠＝∠，∴△∽△，∴＝，即＝·.．解：()证明：∵＝，∴＝.∵平分∠，∴∠＝∠，∴＝，∴＝，∴＝.()∵四边形＝△＋△.设△和△的公共边上的高分别为，，则＋的最大值为⊙的直径，即当在劣弧的中点、在优弧的中点时，四边形的面积最大，如图，连接，，∵∠＝°，∴∠＝°.∵＝＝，∴＝，∴四边形＝(＋)＝××＝.．解：∵是的中点，∴＝.∵∠＝°，∠与∠是同弧所对的圆周角，∴∠＝°，∴△是等边三角形，∴∠＝∠＝°，∴∠＝∠＝°.∵∥，∴∠＝∠＝°，∴∠＝∠.∵∠＝∠＝°，∴△是等边三角形，∴＝.∵∠与∠是同弧所对的圆周角，∴∠＝∠.在△和△中，∠＝∠，∠＝∠，＝，∴△≌△()，∴＝＝.[素养提升]解：()如图①，连接.∵的度数为°，的度数为°，∴∠＝×°＝°，∠＝×°＝°，∴∠＝∠－∠＝°.图①图②()圆外角的性质：圆外角的度数等于它所对的较大弧的度数减去较小弧的度数所得差的一半．理由：如图①.∵圆周角的度数等于它所对弧的度数的一半，∴∠＝×的度数，∠＝×的度数，∴∠＝∠－∠＝(的度数－的度数)，∴圆外角的度数等于它所对的较大弧的度数减去较小弧的度数所得差的一半．()把顶点在圆内，并且两边都和圆相交的角叫圆内角，性质：圆内角的度数等于它和它的对顶角所对两弧的度数和的一半．证明：如图②，延长交⊙于点，延长交⊙于点，连接.∵∠是△的一个外角，∴∠＝∠＋∠.∵圆周角的度数等于它所对弧的度数的一半，∴∠＝×的度数，∠＝×的度数．∴∠＝∠＋∠＝×的度数＋×的度数＝(的度数＋的度数)．。

第2课时 圆周角定理与推论11.如图，已知圆心角∠BOC ＝78°，则圆周角∠BAC 的度数是( )[来源:]A ．156°B ．78°C ．39°D ．12°2.圆周角是24°，则它所对的弧是( )[来源:Z.xxA ．12°B ．24°C ．36D ．48°3.如图，在⊙O 中，若C 是»BD的中点，则图中与∠BAC 相等的角有（ ） A.1个 B.2 个 C.3个 D.4个4.如图，AB 、CD 是⊙O 的两条弦，连接AD 、BC ，若∠BAD=60°，则∠BCD 的度数为（ ）A.40°B.50°C.60°D.70°5.如图，在⊙O 中，∠AOB 的度数为m ，C 是ACB ︵上一点，D ，E 是AB ︵上不同的两点(不与A ，B 两点重合)，则∠D ＋∠E 的度数为()A ．mB ．180°－m 2C ．90°＋m 2D ．m 2[来源:学科网] 6.如图，AB 是 ⊙O 的直径，BC⌒ =BD ⌒ ,∠A=25°， 则∠BOD= . C· B D OAODCBA7.如图，已知点E是圆O上的点，B，C是AD︵的三等分点，∠BOC＝46°，则∠AED的度数为________．8.如图，在⊙O中，F，G是直径AB上的两点，C，D,E是半圆上的三点，如果弧AC的度数为60°，弧BE的度数为20°，∠CF A=∠DFB，∠DGA=∠EG B．求∠FDG的大小9.如图，以⊙O的直径BC为一边作等边△ABC,AB、AC交⊙O于D、E,求证：BD=DE=EC10.如图，在锐角△ABC中，AB＞AC，AD⊥BC于点D，以AD为直径的⊙O分别交AB，AC于点E，F，连接DE，DF.:学科网ZXXK](1)求证：∠EAF＋∠EDF＝180°.(2)已知P是射线DC上一个动点，当点P运动到PD＝BD时，连接AP，交⊙O于点G，连接DG.设∠EDG＝∠α，∠APB＝∠β，那么∠α与∠β有何数量关系？试证明你的结论(在探究∠α与∠β的数量关系时，必要时可直接运用(1)的结论进行推理与解答)．。