虚拟变量(哑变量)回归

logistic回归哑变量结果解读在进行logistic回归时，若自变量包含非连续变量，常常使用哑变量处理方法转换为数值型变量进行回归分析。

哑变量在结果解释中常常是一个重要的部分，以下是对哑变量结果的解读。

1. 哑变量及其一个水平的基准值。

哑变量是指将分类变量拆分成两个或多个虚拟变量。

例如，在分析某地区居住状态是否对健康的影响时，人们会将居住状态分为有房无贷、有房有贷、租房三类。

此时，需要将该分类变量转换成虚拟变量。

分别用两个虚拟变量来表示“有房有贷”和“租房”的情况，而“有房无贷”则成为基准值。

2. coefficients系数。

这是指logistic回归模型中哑变量所对应的系数值。

例如，在上例中，如果哑变量为“有房有贷”，一旦计算出回归系数后，可以得到如下方程：β0 + β1x1，其中x1是有没有房贷（0代表无房贷，1代表有房贷），β0是常数项，β1为有房贷的系数。

3. 每个水平与基准水平之间的比较。

利用上述方程，可以通过系数来判断每个水平与基准水平之间的比较。

在此例中，如果水平1是“有房有贷”，水平2是“租房”，那么如果得到的回归系数为β0 +β1x1，那么系数1 - 系数2 = β1，这表示“有房有贷”相对于“租房”有更高的健康风险，且差异很显著。

4. 对哑变量结果的显著性检验。

为了知道哑变量效果是否显著，可以使用检验，常常使用卡方检验。

如果显著性检验得到的p值小于0.05，则说明样本之间存在较大差异，在输出结果时需要特别关注。

在哑变量的结果解释中，需要注意的是哑变量是假设变量，所以哑变量的系数的解释需要谨慎。

而且，与其它因素相比，哑变量本身可能是一个较小的影响因素，因此在结果解释中需要用组合变量，即哑变量与其它变量的组合来进行解释。

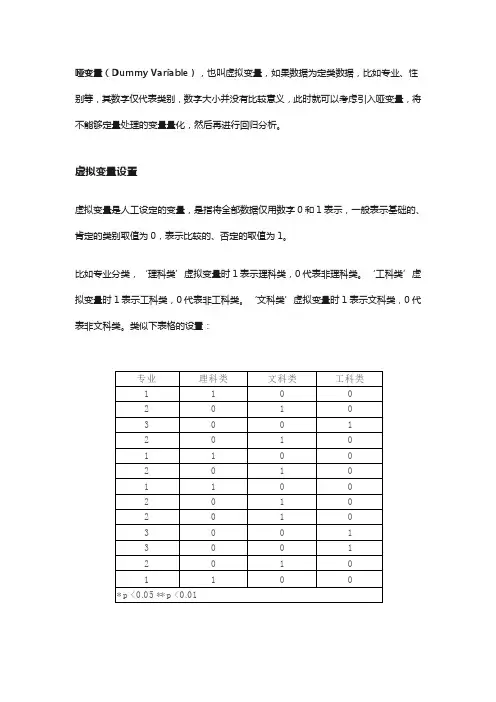
哑变量（Dummy Variable），也叫虚拟变量，如果数据为定类数据，比如专业、性别等，其数字仅代表类别，数字大小并没有比较意义，此时就可以考虑引入哑变量，将
上图中专业分为三类，因而需要设置3个虚拟变量(3列)，分别代表专业的3个类别。

需要特别注意的是，从数学角度来讲，如果专业对应的3个虚拟变量都放入模型，一定会出现‘多重共线性问题’。

原因在于：虚拟变量是数字0和1；0是对比参考项（比如‘相对其它专业即非理科类专业，理科类专业如何如何’）。

所以3个类别都放入了，就没有可参考类别了。

因此在做回归分析时，只需放入2个虚拟变量。

SPSSAU设置虚拟变量
理解虚拟变量的原理后，即可在SPSSAU中进行设置。

用户可在SPSSAU中的‘生成变量’功能可实现虚拟变量设置。

总结
●对于定类变量，进行分析时需要先转化为哑变量。

通常情况下，回归分析，逐步回
归，分层回归，二元Logit回归，多分类Logit回归分析这类影响关系研究的方法时，才可能涉及到虚拟变量设置。

其它分析方法并不会涉及。

●虚拟变量取“1”或“0”的原则，应从分析问题的目的考虑，“1”代表具有特征
的肯定的类别，“0”代表普遍的否定的类别。

●注意虚拟变量放入回归中分析，不能全部放入，会产生共线性问题。

一定要找好参
考对照项，少放入1个虚拟变量。

●如果虚拟变量为2个，比如性别分男和女；这种特殊情况也是类似的处理即可。

设计虚拟变量方法虚拟变量方法（Dummy Variable Method），也称为哑变量方法或指示变量法，是一种常用的统计方法，主要用于处理分类变量在数值分析中的应用问题。

本文将详细讨论虚拟变量方法的原理、应用及优缺点，并举例说明其具体操作步骤。

1. 虚拟变量方法原理虚拟变量方法的核心思想是将分类变量转换为二值的虚拟变量（dummy variable），以便在数值分析中使用。

对于具有n个类别的分类变量，虚拟变量方法将其转化为n个二值变量，每个二值变量代表一个类别。

如果样本属于某个类别，则对应的二值变量取1，否则为0。

2. 虚拟变量方法的应用虚拟变量方法主要应用于以下两个方面：2.1. 处理分类变量: 在回归分析中，通常只能处理数值型变量。

使用虚拟变量方法，我们可以将分类变量转化为虚拟变量，然后应用回归模型进行分析。

虚拟变量方法在社会科学和经济学等领域有广泛的应用，比如研究不同性别对工资的影响，通过将性别变量转化为虚拟变量，可以确定性别对工资的影响是否显著。

2.2. 建立交互作用: 虚拟变量方法还可以用于研究多个变量之间的关系及其交互作用。

通过将多个分类变量转化为虚拟变量，并进行交叉乘积运算，可以获取不同类别组合的效应差异，进而分析各个变量之间的关系。

3. 虚拟变量方法的步骤虚拟变量方法的操作步骤如下：3.1. 选择分类变量: 首先需要确定需要转化为虚拟变量的分类变量。

3.2. 创建虚拟变量: 对于n个类别的分类变量，创建n-1个虚拟变量。

其中，一个类别作为基准类别（reference category），在计算逻辑回归模型时作为参照。

3.3. 赋值: 对于样本中的每一个观测值，根据其所属类别，为相应的虚拟变量赋值。

如果某一样本属于某个类别，则对应的虚拟变量取1，否则为0。

3.4. 分析: 根据创建的虚拟变量，应用适当的统计方法进行分析。

可以使用回归模型、方差分析或卡方检验等方法。

4. 虚拟变量方法的优缺点虚拟变量方法具有以下优点：4.1. 解决了分类变量在数值分析中的应用问题: 虚拟变量方法允许我们在回归分析中使用分类变量，可以更全面地考虑分类变量对结果的影响。

虚拟变量回归
虚拟变量回归是指将一个分类变量转化为虚拟变量（也称为哑变量或指示变量），并将其作为解释变量在回归模型中使用。

虚拟变量是一种二元变量，其中一个变量用1表示某个类别，另一个变量用0表示不属于该类别。

例如，当一个分类变量有三个类别时，可以创建两个虚拟变量来表示这三个类别，分别是0-1变量A和0-1变量B，它们满足如下条件：
- 当分类变量属于A类时，变量A为1，变量B为0；
- 当分类变量属于B类时，变量A为0，变量B为1；
- 当分类变量属于C类时，变量A和变量B均为0。

在回归模型中使用虚拟变量可以使我们将分类变量的不同类别彼此对比，并推断它们对应的不同的回归系数，从而更好地解释和预测因变量。

虚拟变量回归在经济学、社会学、医疗保健等领域中很常见，可以用来研究诸如性别、种族、政治党派、行业等分类变量对某一因变量的影响。

回归模型中的哑变量是个啥？何时需要设置哑变量？在构建回归模型时，如果自变量X为连续性变量，回归系数β可以解释为：在其他自变量不变的条件下，X每改变一个单位，所引起的因变量Y的平均变化量；如果自变量X为二分类变量，例如是否饮酒（1=是，0=否），则回归系数β可以解释为：其他自变量不变的条件下，X=1（饮酒者）与X=0（不饮酒者）相比，所引起的因变量Y 的平均变化量。

但是，当自变量X为多分类变量时，例如职业、学历、血型、疾病严重程度等等，此时仅用一个回归系数来解释多分类变量之间的变化关系，及其对因变量的影响，就显得太不理想。

此时，我们通常会将原始的多分类变量转化为哑变量，每个哑变量只代表某两个级别或若干个级别间的差异，通过构建回归模型，每一个哑变量都能得出一个估计的回归系数，从而使得回归的结果更易于解释，更具有实际意义。

哑变量哑变量（Dummy Variable），又称为虚拟变量、虚设变量或名义变量，从名称上看就知道，它是人为虚设的变量，通常取值为0或1，来反映某个变量的不同属性。

对于有n个分类属性的自变量，通常需要选取1个分类作为参照，因此可以产生n-1个哑变量。

将哑变量引入回归模型，虽然使模型变得较为复杂，但可以更直观地反映出该自变量的不同属性对于因变量的影响，提高了模型的精度和准确度。

举一个例子，如职业因素，假设分为学生、农民、工人、公务员、其他共5个分类，其中以“其他职业”作为参照，此时需要设定4哑变量X1-X4，如下所示：X1=1，学生；X1=0，非学生；X2=1，农民；X2=0，非农民；X3=1，工人；X3=0，非工人；X4=1，公务员；X4=0，非公务员；那么对于每一种职业分类，其赋值就可以转化为以下形式：什么情况下需要设置哑变量1. 对于无序多分类变量，引入模型时需要转化为哑变量举一个例子，如血型，一般分为A、B、O、AB四个类型，为无序多分类变量，通常情况下在录入数据的时候，为了使数据量化，我们常会将其赋值为1、2、3、4。

多元逻辑斯蒂回归哑变量一、引言多元逻辑斯蒂回归（Multinomial Logistic Regression，MLR）是一种广泛用于分类问题的统计学习方法。

当自变量与因变量之间存在非线性关系或自变量之间的交互效应较强时，传统的线性回归模型可能无法准确地预测因变量，而多元逻辑斯蒂回归在这种情况下表现优异。

在多元逻辑斯蒂回归中，哑变量（Dummy Variables）是一种常见的处理分类变量的方法，它可以解决分类变量不能直接进入线性回归模型的问题。

二、多元逻辑斯蒂回归中的哑变量哑变量在多元逻辑斯蒂回归中起着至关重要的作用。

由于逻辑斯蒂回归是一个基于概率的二项式回归模型，因此无法直接使用分类自变量。

为了将分类自变量引入模型，需要将其转换为哑变量。

哑变量是一种虚拟变量，用于表示分类变量的不同类别。

通过将每个类别表示为一个虚拟变量，可以模拟分类变量与因变量之间的非线性关系。

三、哑变量的构造构造哑变量的基本步骤如下：1.确定分类变量的类别数量。

2.为每个类别创建一个虚拟变量。

3.将虚拟变量引入模型，并指定一个参考类别作为参照点。

4.为每个虚拟变量指定一个截距，以反映该类别的平均效应。

5.估计模型参数，以确定每个类别的相对风险或概率。

四、哑变量的解释在多元逻辑斯蒂回归中，哑变量的解释对于理解模型的输出至关重要。

以下是一些解释哑变量的要点：1.参照组选择：在逻辑斯蒂回归中，通常选择一个参照组作为基准类别。

该参照组在模型中通过截距项表示，所有其他类别的效应则通过与之比较的虚拟变量来解释。

因此，参照组的效应是所有其他类别的平均效应。

2.效应估计：通过估计每个虚拟变量的系数，可以了解各个类别相对于参照组的效应。

具体来说，系数的大小和符号可以揭示各个类别的风险或概率与参照组相比有何不同。

如果某个类别的系数为正数，则表示该类别的风险或概率高于参照组；如果系数为负数，则表示低于参照组。

3.交互效应：通过引入多个哑变量，可以模拟分类自变量之间的交互效应。

虚拟变量熵权法-回复什么是虚拟变量和熵权法，并介绍它们的应用。

在统计学和机器学习领域，虚拟变量（Dummy variable）和熵权法（Entropy weighting）是两个常用的概念和方法。

虚拟变量是一种在回归分析和实证研究中常用的数值表示方法，而熵权法是一种多指标综合评价方法。

下面将一步一步回答关于虚拟变量和熵权法的问题。

一、什么是虚拟变量？虚拟变量又称为哑变量或指示变量，在数学和统计学中，是用来表示分类变量的一种数值表示方法。

通常情况下，分类变量是离散的，比如性别、国籍等。

虚拟变量可以将这些分类变量编码为数值，用0和1表示。

虚拟变量的编码规则是，为每个分类变量设定一个虚拟变量，如果观测数据属于某一类别，则该虚拟变量取值为1，否则为0。

这种编码方式可以有效地将分类变量引入回归模型中。

虚拟变量的使用可以帮助解决回归分析中的一些问题，比如处理分类变量、多组比较和交互效应等。

在实际应用中，虚拟变量的使用非常广泛，比如用来研究不同性别对收入的影响、不同地区对销售额的影响等。

二、什么是熵权法？熵权法是一种多指标综合评价方法，用来确定多个指标的权重以及指标之间的重要性关系。

该方法基于信息熵原理，通过计算指标的信息熵来确定其权重。

熵是度量信息的不确定性的指标，表示了信息的平均信息量。

在熵权法中，先计算每个指标的熵值，然后根据熵值大小来确定其权重。

熵值越大，代表了指标的不确定性越高，权重越小；反之，熵值越小，代表了指标的不确定性越小，权重越大。

熵权法的优点是能够考虑到指标之间的相互影响和重要性关系，从而更准确地反映多指标下的综合评价结果。

该方法在决策分析、风险评估和投资评价等领域得到了广泛的应用。

三、虚拟变量和熵权法的应用虚拟变量和熵权法在不同领域有着各自的应用。

虚拟变量在回归分析中的应用很广泛。

通过将分类变量转化为虚拟变量，可以将其引入回归模型中，从而探究不同类别对因变量的影响。

比如，研究性别对工资的影响时，可以将性别编码为虚拟变量，然后用回归模型来解释工资与性别之间的关系。

逻辑回归是一种常用的统计建模方法，它经常用于预测二元变量的取值情况。

在逻辑回归中，有时候我们需要考虑一些非数值型的变量，这时候就需要使用哑变量进行编码，以便将非数值型变量转换为适合逻辑回归分析的数值型变量。

1. 什么是哑变量哑变量，又称虚拟变量或指示变量，是一种用来表示类别型数据的变量。

在逻辑回归中，我们需要将非数值型的变量转换为哑变量，以便用于模型的建立和预测。

2. 哑变量的变化方式在将非数值型变量转换为哑变量时，通常采用的方式是一对多或者多对多的编码方式。

一对多编码方式是将一个类别型变量转换为多个哑变量，每个哑变量对应该变量的一个类别。

多对多编码方式则是将一个类别型变量转换为多个哑变量，同时每个哑变量可以代表多个类别。

3. 哑变量的作用使用哑变量的目的主要包括两点：一是避免对类别型变量的错误排名，二是利用哑变量表示不同类别之间的差异。

4. 实例分析举例说明，假设有一个数据集包含了性莂这个变量，其中男性和女性用"男"和"女"表示。

为了将性莂转换为适合逻辑回归分析的数值型变量，我们可以采用一对多的编码方式。

具体做法是创建一个名为"性莂_男"的哑变量，当该样本为男性时，性莂_男等于1，否则为0；再创建一个名为"性莂_女"的哑变量，当该样本为女性时，性莂_女等于1，否则为0。

通过这种方式，我们成功地将性莂这一非数值型变量转换为了适合逻辑回归分析的数值型变量。

5. 哑变量的注意事项在进行逻辑回归分析时，需要注意以下几点：- 避免完全多重共线性：每一个哑变量都应该是完整的，不应该包含多余的信息。

- 避免虚构多重共线性：哑变量要避免陷入虚构多重共线性的误区，即一个哑变量的线性组合不能完全等于另一个哑变量。

- 寻找基准类别：在使用一对多的编码方式时，需要选择一个类别作为基准类别，其他类别相对于该基准类别进行编码，以避免虚构多重共线性的问题。

虚拟变量案例stata
1.定义
引入“虚拟变量（哑变量，dummy variable）”对定性数据或者分类数据，赋值0或者1。

例如，对东部、中部、西部产生虚拟变量，则需要2个。

因为east=1，表示东部；east=0，表示其他地区。

同样middle=1，表示中部；middle=0，表示其他地区。

那么east=0，且middle=0时，则表示west（西部）。

但是值得注意的是，（east=1的个数）+（middle=1的个数）+（表示west的数值）=全体分析样本数。

否则，在stata回归时不会自动检测到多重共线性，自动omit 其中一个变量。

2.设置参照组
下面例子中：east=1，表示东部；middle=1，表示中部；west= 1，表示西部。

目的是为了选择参照组。

"note:west omitted because of collinearity"：我把三个变量都放进去，所以stata检测到多重共线性，把west的变量忽略了，作为参照组（对比组）。

如果想把参照组设定为middle：
reg ln_min edu east west
如果想把参照组设定为east：
reg ln_min edu middle west
或者在回归中指定omit variable：。

虚拟变量陷阱名词解释计量经济学1.引言概述部分主要介绍虚拟变量陷阱的基本概念和背景信息。

以下是对概述部分内容的一种可能的编写方式：1.1 概述在统计学和经济学等领域中，虚拟变量是一种常用的数据处理技术，用于将非连续的定性变量转化为对应的哑变量或二进制变量。

虚拟变量的引入有助于通过回归分析研究变量之间的关系，并且常用于解释定性因素对于结果变量的影响程度。

然而，虚拟变量的应用也存在着一个潜在的问题，即虚拟变量陷阱。

虚拟变量陷阱（Dummy Variable Trap）指的是在回归分析中，由于自变量之间存在完全多重共线性，导致回归系数估计出现扭曲、不稳定甚至无意义的现象。

具体来说，虚拟变量陷阱会使得回归模型的解释变得困难，而且可能会对模型的预测能力产生负面影响。

通常情况下，虚拟变量陷阱会在引入全部虚拟变量作为自变量时出现。

这是因为当我们引入一个包含K个类别的定性变量时，一般会通过引入K-1个虚拟变量来表征不同的类别，其中一个类别作为基准类别。

然而，如果我们同时引入了全部K个虚拟变量，就会引入完全多重共线性，从而导致虚拟变量陷阱的发生。

在本文中，我们将详细探讨虚拟变量陷阱的概念、影响和避免方法。

通过了解虚拟变量陷阱的本质和原因，我们可以更准确地应用虚拟变量，并确保回归分析的结果可信、有效。

接下来的章节将从定义和作用开始，逐步展开对虚拟变量陷阱的解释和分析。

然后，我们将探讨虚拟变量陷阱可能产生的影响，并提供一些避免虚拟变量陷阱的实用经验和方法。

通过深入研究和论证，我们旨在为读者提供一个全面且实用的虚拟变量陷阱指南。

【1.2 文章结构】本文将分为以下几个部分来讨论虚拟变量陷阱，以帮助读者更好地理解和避免这个常见的统计分析问题。

首先，在引言部分，我们将概述文章的主题和目的。

然后，我们将介绍文章的整体结构，以指导读者对整篇文章的理解和阅读方式。

接下来，我们将进入正文部分。

首先，我们会对虚拟变量进行定义和解释其作用。

多分类逻辑回归设置哑变量哑变量在多分类逻辑回归中的应用在多分类逻辑回归中，哑变量是一种重要的数据处理方式。

本文将从什么是哑变量、哑变量在多分类逻辑回归中的作用以及如何使用哑变量进行数据处理等方面展开讨论。

一、什么是哑变量哑变量（Dummy Variable），也称为虚拟变量，是一种用来表示分类变量的技术。

在多分类逻辑回归中，我们常常需要处理具有多个类别的自变量。

为了能够在模型中使用这些类别变量，需要将其转换为数值变量。

而哑变量就是将类别变量转化为二进制变量的一种方法。

二、哑变量在多分类逻辑回归中的作用在多分类逻辑回归中，哑变量的作用是将具有多个类别的自变量进行编码，使得模型能够处理这些类别变量。

通过将类别变量转化为二进制变量，可以将每个类别都表示为一个单独的变量。

这样一来，模型就可以根据这些变量的取值来预测不同类别的概率。

三、如何使用哑变量进行数据处理使用哑变量进行数据处理主要包括两个步骤：变量编码和数据拆分。

1. 变量编码变量编码是将类别变量转化为哑变量的过程。

通常情况下，如果一个类别变量有k个不同的取值，那么就需要创建k-1个哑变量。

这是因为在多分类逻辑回归中，如果我们使用k个哑变量来表示k个类别，那么会存在多重共线性的问题。

因此，我们通常将其中一个类别作为参照类别，不创建对应的哑变量。

2. 数据拆分在将类别变量转化为哑变量后，我们需要将原始数据集拆分为训练集和测试集。

拆分的目的是为了在模型训练和验证时能够使用不同的数据集。

通常情况下，我们将大部分数据用于模型训练，少部分数据用于模型验证。

四、哑变量的优势与注意事项哑变量在多分类逻辑回归中具有以下优势：1. 提供了一种将类别变量转化为数值变量的方法，使得模型能够处理这些变量；2. 通过使用哑变量，可以更好地捕捉不同类别之间的差异，提高模型的预测能力。

然而，在使用哑变量时也需要注意以下事项：1. 每个类别变量都应该有足够的样本量，以确保每个类别的哑变量都能够提供有效的信息；2. 在创建哑变量时，应该选择一个合适的参照类别，以避免多重共线性问题。

stata分类变量哑变量cox回归-回复Stata中使用分类变量进行Cox回归分析的方法概述：在统计分析中，分类变量被广泛应用于Cox回归（一种生存分析方法），以探究分类变量对事件发生的影响。

而对于类似的分析，Stata是一个功能强大且常用的统计分析软件，它提供了丰富的功能来处理和分析生存数据。

在本文中，我们将以Stata中的分类变量和Cox回归模型为主题，讲解如何进行Cox回归分析。

1. 数据准备：首先，我们需要确保数据集应当具有以下两个要素：时间变量和事件变量。

时间变量描述了每个观察对象的时间点，并且事件变量表示了在该时间点是否发生了该事件。

这些数据可以是实际数据或是模拟数据。

2. 创建哑变量：在分类变量存在的情况下，我们需要将其转换为哑变量。

哑变量是指一个用二进制表示的虚拟变量，它表示了原始分类变量的每一类别。

在Stata 中，我们可以使用"tabulate"或"tab"命令来查看分类变量的频率分布情况，并基于这些结果来创建哑变量。

这里需要注意的是，在创建哑变量之前，我们需要为分类变量赋予正确的标签。

3. 转换为Cox回归可行的格式：在进行Cox回归分析之前，我们需要将数据集转换为Stata中可以接受的格式。

在这里，我们需要按照Stata的要求，确保数据集具有以下的格式：每一行表示一个观察对象，每一列表示一个变量，其中包括时间变量、事件变量和创建的哑变量。

4. 进行Cox回归分析：一旦数据集准备好了，我们就可以开始进行Cox回归分析。

在Stata中，可以使用"stcox"命令来执行Cox回归分析。

命令的常见参数包括时间变量、事件变量以及用于控制其他潜在影响因素的变量。

5. 回归结果的解释：在得到Cox回归结果之后，我们需要解释它们以获得有关分类变量和事件发生之间关系的信息。

对于每个哑变量，我们可以通过估计的回归系数（beta值）来衡量其影响，其中正值表示正向影响，负值表示负向影响，而系数为零表示没有影响。