第八章虚拟变量回归知识讲解

第八章虚拟变量模型1. 回归模型中引入虚拟变量的作用是什么?答:在模型中引入虚拟变量，主要是为了寻找某(些)定性因素对解释变量的影响。

加法方式与乘法方式是最主要的引入方式，前者主要适用于定性因素对截距项产生影响的情况，后者主要适用于定性因素对斜率项产生影响的情况。

除此外，还可以加法与乘法组合的方式引入虚拟变量，这时可测度定性因素对截距项与斜率项同时产生影响的情况。

2. 虚拟变量有哪几种基本的引入方式? 它们各适用于什么情况?答:在模型中引入虚拟变量的主要方式有加法方式与乘法方式，前者主要适用于定性因素对截距项产生影响的情况，后者主要适用于定性因素对斜率项产生影响的情况。

除此外，还可以加法与乘法组合的方式引入虚拟变量，这时可测度定性因素对截距项与斜率项同时产生影响的情况。

3．什么是虚拟变量陷阱？答：根据虚拟变量的设置原则，一般情况下，如果定性变量有m个类别，则需在模型中引入m-1个变量。

如果引入了m个变量，就会导致模型解释变量出现完全的共线性问题，从而导致模型无法估计。

这种由于引入虚拟变量个数与类别个数相等导致的模型无法估计的问题，称为“虚拟变量陷阱”。

4．在一项对北京某大学学生月消费支出的研究中，认为学生的消费支出除受其家庭的每月收入水平外，还受在学校中是否得到奖学金，来自农村还是城市，是经济发达地区还是欠发达地区，以及性别等因素的影响。

试设定适当的模型，并导出如下情形下学生消费支出的平均水平：(1) 来自欠发达农村地区的女生，未得到奖学金；(2) 来自欠发达城市地区的男生，得到奖学金；(3) 来自发达地区的农村女生，得到奖学金；(4) 来自发达地区的城市男生，未得到奖学金。

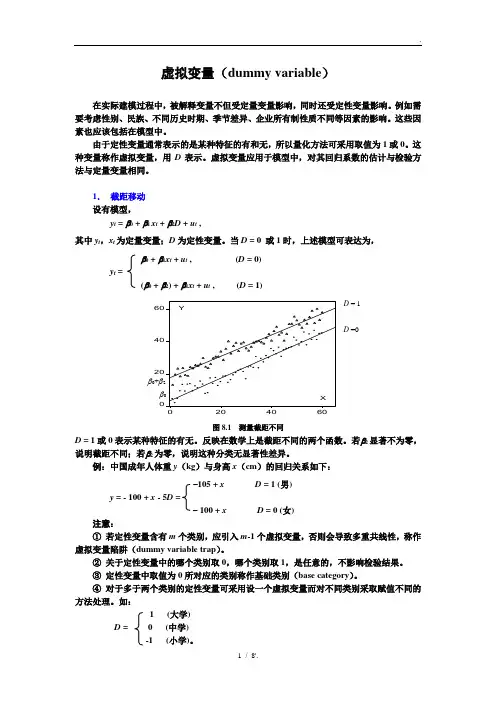
解答: 记学生月消费支出为Y，其家庭月收入水平为X，则在不考虑其他因素的影响时，有如下基本回归模型：Y i=β0+β1X i+μi有奖学金1 来自城市无奖学金0 来自农村来自发达地区 1 男性0 来自欠发达地区0 女性Y i=β0+β1X i+α1D1i+α2D2i+α3D3i+α4D4i+μi由此回归模型，可得如下各种情形下学生的平均消费支出：(1) 来自欠发达农村地区的女生，未得到奖学金时的月消费支出：E(Y i|= X i, D1i=D2i=D3i=D4i=0)=β0+β1X i(2) 来自欠发达城市地区的男生，得到奖学金时的月消费支出：E(Y i|= X i, D1i=D4i=1,D2i=D3i=0)=(β0+α1+α4)+β1X i(3) 来自发达地区的农村女生，得到奖学金时的月消费支出：E(Y i |= X i , D 1i =D 3i =1,D 2i =D 4i =0)=(β0+α1+α3)+β1X i (4) 来自发达地区的城市男生，未得到奖学金时的月消费支出： E(Y i |= X i ,D 2i =D 3i =D 4i =1, D 1i =0)= (β0+α2+α3+α4)+β1X i5. 研究进口消费品的数量Y 与国民收入X 的模型关系时，由数据散点图显示1979年前后Y 对X 的回归关系明显不同，进口消费函数发生了结构性变化：基本消费部分下降了，而边际消费倾向变大了。

stata虚拟变量的回归命令虚拟变量是用来表示分类变量的一种方法，它可以将分类变量转换为一系列二进制变量，每个二进制变量表示分类变量的一个类别。

这样，就可以使用回归模型来分析分类变量对因变量的影响。

stata中有多个回归命令可以用于分析虚拟变量，包括：•regress：这是最基本的回归命令，可以用于分析连续因变量和分类自变量之间的关系。

•logit：这是一个非线性回归命令，可以用于分析二分类因变量和分类自变量之间的关系。

•probit：这是一个非线性回归命令，可以用于分析二分类因变量和分类自变量之间的关系。

•poisson：这是一个非线性回归命令，可以用于分析计数因变量和分类自变量之间的关系。

在stata中使用虚拟变量回归命令时，需要特别注意以下几点：•虚拟变量的个数：分类变量的类别数决定了虚拟变量的个数。

例如，一个有3个类别的分类变量需要创建2个虚拟变量。

•虚拟变量的取值：虚拟变量的取值为0或1，其中0表示分类变量不属于该类别，1表示分类变量属于该类别。

•虚拟变量的解释：虚拟变量的系数表示分类变量的每个类别对因变量的影响。

例如，一个虚拟变量的系数为正，表示该类别对因变量有正向影响；一个虚拟变量的系数为负，表示该类别对因变量有负向影响。

下面是一个stata虚拟变量回归命令的例子：regress y x1 x2 x3logistic y x1 x2 x3poisson y x1 x2 x3在这个例子中，y是因变量，x1、x2和x3是分类自变量。

regress命令用于分析y和x1、x2、x3之间的线性关系，logistic命令用于分析y和x1、x2、x3之间的非线性关系，poisson命令用于分析y和x1、x2、x3之间的非线性关系。

虚拟变量回归命令是stata中非常重要的一个工具，它可以用于分析分类变量对因变量的影响。

在使用虚拟变量回归命令时，需要特别注意虚拟变量的个数、虚拟变量的取值和虚拟变量的解释。

对外经济贸易大学计量经济学I n t r o d u c t i o n t o E c o n o m e t r i c s导论虚拟变量的定义与含单个虚拟变量的回归定性信息在前面的章节中，我们见到的变量都是用来描述定量信息的，比如考试分数，生师比，工资，股本回报率等等；然而，在经济学研究中，往往有很多的定性信息，比如性别，地域，种族，是否实施某项政策等等。

在模型中引入定性信息需要用到虚拟变量。

虚拟变量虚拟变量是值为0或1的变量例1：Male i= 1如果工人i为男性0如果工人i为女性例2：South i= 1如果国家i为南方国家0如果国家i为北方国家因此，虚拟变量也叫二元变量 (Binary Variable)或者哑元变量（Dummy Variable）。

带定性变量的数据名称应反映编码值二元变量的名称应反映变量的定义。

例如，名为“性别”的变量不清楚哪一个是1，而变量名称“Female”则更清楚。

不同的定义方式有不同的解释。

两个组别的定性变量可以使用一个二元变量，多个组别的定性变量应该使用一组二元变量。

含有一个虚拟自变量的回归例：工资的性别差异定义一个虚拟变量femalewage= β0+β1edu+δ0femaleE wage edu,female=0=β0+β1eduE wage edu,female=1=(β0+δ0)+β1edu工资的性别差异δ0可视为给定教育水平的情况下，女性与男性的平均工资之差。

含有一个虚拟自变量的回归一般地，考虑一个带有一个连续变量（x）和一个虚拟（d）的简单模型。

y = b0 + d0d + b1x + uE y x,d=0=β0+β1xE y x,d=1=(β0+δ0)+β1x因此δ0=E y x,d=1−E y x,d=0可以解释成为两个组别的均值之差，其中d =0的组为基准组。

基准组与比较组在上述例子中，female i= 1如果工人i为女性0如果工人i为男性男性是基准组，女性是比较组，δ0可视为给定教育水平的情况下，女性与男性的平均工资之差。