虚拟变量(哑变量)回归

虚拟变量的名词解释在数据分析和统计学中，虚拟变量是一种常用的变量类型。

虚拟变量，也被称为哑变量或指示变量，通常用来表示分类变量的不同水平或类别。

虚拟变量在数据分析中起到了至关重要的作用。

通过将分类变量转化为虚拟变量，我们能够使用数值变量来表示不同的类别，并在统计模型中使用。

这样做的好处是可以将分类变量的影响纳入模型中，而不是简单地将其作为单一的类别。

虚拟变量通常采用二元编码方式来表示分类变量的不同类别。

举个例子，假设我们有一个分类变量是颜色，可能有红、蓝、绿三个类别。

我们可以使用两个虚拟变量来表示这三个类别，比如我们可以设定一个虚拟变量为红色，取值为1表示观测值为红色，取值为0表示观测值不是红色；另外一个虚拟变量设定为蓝色，同样取值为1或0。

这样，对于每个观测值，我们可以用两个二元变量表示其颜色。

虚拟变量在回归分析中特别有用。

通过将分类变量转化为虚拟变量后，我们可以将其纳入回归模型中进行分析。

以线性回归为例，如果我们的自变量包含一个虚拟变量，我们可以在回归模型中将其作为一个系数进行解释。

假设这个虚拟变量是性别，取值为1表示男性，取值为0表示女性。

在回归模型中，该虚拟变量的系数，即回归系数，可以解释男性和女性在因变量上的平均差异。

另一个常见的用途是在分类器和机器学习算法中。

虚拟变量可以作为输入特征，帮助机器学习算法区分不同的类别。

比如，在邮件垃圾分类器中，我们可以使用虚拟变量表示是否包含某个关键词，而分类器可以根据虚拟变量的取值来判断邮件是否是垃圾邮件。

此外，虚拟变量还可以消除分类变量之间的顺序关系。

有时候，分类变量之间存在不同的大小或顺序。

例如，季节变量可以表示春季、夏季、秋季和冬季。

如果我们简单地将这个分类变量用1、2、3、4来编码，模型可能会误认为这是一种连续变量，并对它们的大小加以解释。

为了消除这种顺序关系，我们可以将这个分类变量转化为三个虚拟变量，每个季节一个虚拟变量，使得其取值只能为0或1，而不再具有顺序性。

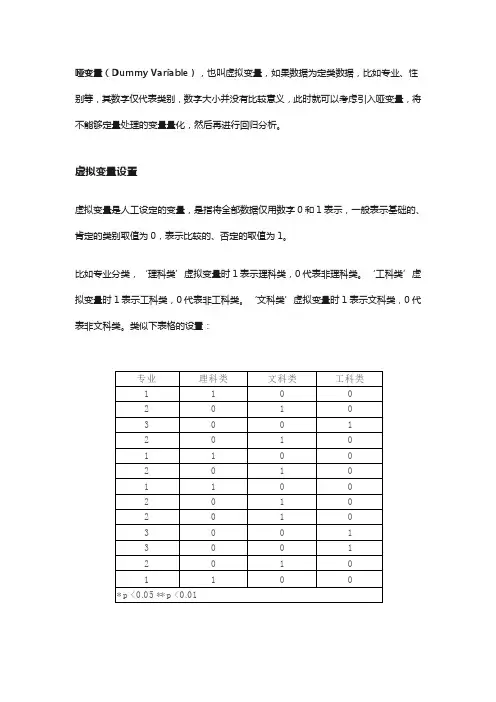
哑变量（Dummy Variable），也叫虚拟变量，如果数据为定类数据，比如专业、性别等，其数字仅代表类别，数字大小并没有比较意义，此时就可以考虑引入哑变量，将
上图中专业分为三类，因而需要设置3个虚拟变量(3列)，分别代表专业的3个类别。

需要特别注意的是，从数学角度来讲，如果专业对应的3个虚拟变量都放入模型，一定会出现‘多重共线性问题’。

原因在于：虚拟变量是数字0和1；0是对比参考项（比如‘相对其它专业即非理科类专业，理科类专业如何如何’）。

所以3个类别都放入了，就没有可参考类别了。

因此在做回归分析时，只需放入2个虚拟变量。

SPSSAU设置虚拟变量
理解虚拟变量的原理后，即可在SPSSAU中进行设置。

用户可在SPSSAU中的‘生成变量’功能可实现虚拟变量设置。

总结
●对于定类变量，进行分析时需要先转化为哑变量。

通常情况下，回归分析，逐步回
归，分层回归，二元Logit回归，多分类Logit回归分析这类影响关系研究的方法时，才可能涉及到虚拟变量设置。

其它分析方法并不会涉及。

●虚拟变量取“1”或“0”的原则，应从分析问题的目的考虑，“1”代表具有特征
的肯定的类别，“0”代表普遍的否定的类别。

●注意虚拟变量放入回归中分析，不能全部放入，会产生共线性问题。

一定要找好参
考对照项，少放入1个虚拟变量。

●如果虚拟变量为2个，比如性别分男和女；这种特殊情况也是类似的处理即可。

设计虚拟变量方法虚拟变量方法（Dummy Variable Method），也称为哑变量方法或指示变量法，是一种常用的统计方法，主要用于处理分类变量在数值分析中的应用问题。

本文将详细讨论虚拟变量方法的原理、应用及优缺点，并举例说明其具体操作步骤。

1. 虚拟变量方法原理虚拟变量方法的核心思想是将分类变量转换为二值的虚拟变量（dummy variable），以便在数值分析中使用。

对于具有n个类别的分类变量，虚拟变量方法将其转化为n个二值变量，每个二值变量代表一个类别。

如果样本属于某个类别，则对应的二值变量取1，否则为0。

2. 虚拟变量方法的应用虚拟变量方法主要应用于以下两个方面：2.1. 处理分类变量: 在回归分析中，通常只能处理数值型变量。

使用虚拟变量方法，我们可以将分类变量转化为虚拟变量，然后应用回归模型进行分析。

虚拟变量方法在社会科学和经济学等领域有广泛的应用，比如研究不同性别对工资的影响，通过将性别变量转化为虚拟变量，可以确定性别对工资的影响是否显著。

2.2. 建立交互作用: 虚拟变量方法还可以用于研究多个变量之间的关系及其交互作用。

通过将多个分类变量转化为虚拟变量，并进行交叉乘积运算，可以获取不同类别组合的效应差异，进而分析各个变量之间的关系。

3. 虚拟变量方法的步骤虚拟变量方法的操作步骤如下：3.1. 选择分类变量: 首先需要确定需要转化为虚拟变量的分类变量。

3.2. 创建虚拟变量: 对于n个类别的分类变量，创建n-1个虚拟变量。

其中，一个类别作为基准类别（reference category），在计算逻辑回归模型时作为参照。

3.3. 赋值: 对于样本中的每一个观测值，根据其所属类别，为相应的虚拟变量赋值。

如果某一样本属于某个类别，则对应的虚拟变量取1，否则为0。

3.4. 分析: 根据创建的虚拟变量，应用适当的统计方法进行分析。

可以使用回归模型、方差分析或卡方检验等方法。

4. 虚拟变量方法的优缺点虚拟变量方法具有以下优点：4.1. 解决了分类变量在数值分析中的应用问题: 虚拟变量方法允许我们在回归分析中使用分类变量，可以更全面地考虑分类变量对结果的影响。

虚拟变量回归
虚拟变量回归是指将一个分类变量转化为虚拟变量（也称为哑变量或指示变量），并将其作为解释变量在回归模型中使用。

虚拟变量是一种二元变量，其中一个变量用1表示某个类别，另一个变量用0表示不属于该类别。

例如，当一个分类变量有三个类别时，可以创建两个虚拟变量来表示这三个类别，分别是0-1变量A和0-1变量B，它们满足如下条件：
- 当分类变量属于A类时，变量A为1，变量B为0；
- 当分类变量属于B类时，变量A为0，变量B为1；
- 当分类变量属于C类时，变量A和变量B均为0。

在回归模型中使用虚拟变量可以使我们将分类变量的不同类别彼此对比，并推断它们对应的不同的回归系数，从而更好地解释和预测因变量。

虚拟变量回归在经济学、社会学、医疗保健等领域中很常见，可以用来研究诸如性别、种族、政治党派、行业等分类变量对某一因变量的影响。

解释哑变量回归中各参数的含义解释哑变量回归中各参数的含义在回归分析中，哑变量回归是一种常用的方法，特别适用于处理分类变量。

在使用哑变量回归时，我们通常会遇到一些参数，如截距项、系数等，这些参数都有着重要的含义和作用。

在本文中，我将从深度和广度的角度，全面解释哑变量回归中各参数的含义，并根据指定的主题文字，进行详细探讨。

1. 截距项在哑变量回归中，截距项是一个非常重要的参数。

它代表了在所有解释变量都为0时，因变量的均值或期望值。

具体来说，如果我们将分类变量转化为哑变量后，在回归模型中将会有一个截距项。

这个截距项的值代表了分类变量的参照组的均值或期望值。

如果我们以性别为分类变量，将其转化为哑变量后，得到性别为男的哑变量和性别为女的哑变量。

那么截距项代表的就是男性的均值或期望值。

2. 哑变量系数在哑变量回归中，每个分类变量的哑变量都会有一个系数与之对应。

这个系数代表了该分类变量对因变量的影响。

当哑变量取值为1时，该系数代表了相应分类变量的均值或期望值与参照组的均值或期望值的差异。

哑变量系数反映了分类变量对因变量的影响大小。

通过对系数的显著性检验，我们可以确定分类变量对因变量的确切影响情况。

3. 交互作用项除了截距项和哑变量系数外，有时我们还会在哑变量回归模型中加入交互作用项。

交互作用项是用来探讨两个或多个变量之间的相互作用关系的。

在哑变量回归中，我们可以使用交互作用项来探讨不同分类变量之间的影响是否相互影响，以及相互影响的程度如何。

通过交互作用项，我们可以更深入地了解分类变量之间的复杂关系。

4. 总结与回顾哑变量回归中的各参数都有着重要的含义和作用。

截距项代表了分类变量的参照组的均值或期望值；哑变量系数反映了分类变量对因变量的影响大小；交互作用项则用于探讨不同分类变量之间的相互影响关系。

这些参数的合理解释和应用，可以帮助我们更好地理解和分析分类变量对因变量的影响。

5. 个人观点在实际数据分析中，哑变量回归是非常常用的方法之一。

回归模型中的哑变量是个啥？何时需要设置哑变量？展开全文在构建回归模型时，如果自变量X为连续性变量，回归系数β可以解释为：在其他自变量不变的条件下，X每改变一个单位，所引起的因变量Y的平均变化量；如果自变量X为二分类变量，例如是否饮酒（1=是，0=否），则回归系数β可以解释为：其他自变量不变的条件下，X=1（饮酒者）与X=0（不饮酒者）相比，所引起的因变量Y 的平均变化量。

但是，当自变量X为多分类变量时，例如职业、学历、血型、疾病严重程度等等，此时仅用一个回归系数来解释多分类变量之间的变化关系，及其对因变量的影响，就显得太不理想。

此时，我们通常会将原始的多分类变量转化为哑变量，每个哑变量只代表某两个级别或若干个级别间的差异，通过构建回归模型，每一个哑变量都能得出一个估计的回归系数，从而使得回归的结果更易于解释，更具有实际意义。

哑变量哑变量（Dummy Variable），又称为虚拟变量、虚设变量或名义变量，从名称上看就知道，它是人为虚设的变量，通常取值为0或1，来反映某个变量的不同属性。

对于有n个分类属性的自变量，通常需要选取1个分类作为参照，因此可以产生n-1个哑变量。

将哑变量引入回归模型，虽然使模型变得较为复杂，但可以更直观地反映出该自变量的不同属性对于因变量的影响，提高了模型的精度和准确度。

举一个例子，如职业因素，假设分为学生、农民、工人、公务员、其他共5个分类，其中以“其他职业”作为参照，此时需要设定4哑变量X1-X4，如下所示：X1=1，学生；X1=0，非学生；X2=1，农民；X2=0，非农民；X3=1，工人；X3=0，非工人；X4=1，公务员；X4=0，非公务员；那么对于每一种职业分类，其赋值就可以转化为以下形式：什么情况下需要设置哑变量1. 对于无序多分类变量，引入模型时需要转化为哑变量举一个例子，如血型，一般分为A、B、O、AB四个类型，为无序多分类变量，通常情况下在录入数据的时候，为了使数据量化，我们常会将其赋值为1、2、3、4。

哑变量的多元线性回归分析
哑变量是多元线性回归分析中非常重要的一种方式，它可以帮助我们理解一个变量与另一个变量之间的关系。

在多元线性回归分析中，哑变量是一种表示独立变量的编码方式，用它可以更好地理解和解释变量之间的关系，从而有助于研究人员做出正确的决策。

哑变量的概念源于统计学中的“哑变量”模型，它是一种被应用于非线性模型的变量。

它的特点在于，它不会直接影响分析结果，而是通过加权和代入值的形式来影响结果。

换句话说，它是一种将一个变量中多个水平划分为N个独立变量，分别拟合每一个水平，从而检验模型中变量之间的关系。

哑变量的应用，主要是为了降低多元线性回归分析中出现的多重共线性，在实证分析中，可以使模型适应性更好。

它可以用来模拟变量之间的非线性关系，从而更好地描述变量之间的关系。

因此，在实际应用中，哑变量非常重要，它可以用来更好地刻画潜在变量之间的关系，从而更准确地估计参数，从而得出分析结果。

由于哑变量具有优异的性能，它被广泛应用于经济学、社会学和心理学等领域的实证分析中。

哑变量在多元线性回归分析中已经成为一种基本的分析技术，对许多经济问题的研究产生重要的影响。

哑变量的使用有其特定的方法，首先要确定独立变量，并根据变量的特点，将其分成N类，以表示不同的水平。

接下来，根据独立变量的水平，设定哑变量的系数，在拟合模型时，将哑变量的系数作为参数，用以表达变量之间的关系，最后进行模型诊断，对模型进行优
化，以得出最优结果。

总而言之，哑变量在多元线性回归分析中起着重要作用，它可以用来更准确地分析多元变量之间的关系，为研究人员提供更可靠的结果，从而帮助他们做出正确的决策。

逻辑回归是一种常用的统计建模方法，它经常用于预测二元变量的取值情况。

在逻辑回归中，有时候我们需要考虑一些非数值型的变量，这时候就需要使用哑变量进行编码，以便将非数值型变量转换为适合逻辑回归分析的数值型变量。

1. 什么是哑变量哑变量，又称虚拟变量或指示变量，是一种用来表示类别型数据的变量。

在逻辑回归中，我们需要将非数值型的变量转换为哑变量，以便用于模型的建立和预测。

2. 哑变量的变化方式在将非数值型变量转换为哑变量时，通常采用的方式是一对多或者多对多的编码方式。

一对多编码方式是将一个类别型变量转换为多个哑变量，每个哑变量对应该变量的一个类别。

多对多编码方式则是将一个类别型变量转换为多个哑变量，同时每个哑变量可以代表多个类别。

3. 哑变量的作用使用哑变量的目的主要包括两点：一是避免对类别型变量的错误排名，二是利用哑变量表示不同类别之间的差异。

4. 实例分析举例说明，假设有一个数据集包含了性莂这个变量，其中男性和女性用"男"和"女"表示。

为了将性莂转换为适合逻辑回归分析的数值型变量，我们可以采用一对多的编码方式。

具体做法是创建一个名为"性莂_男"的哑变量，当该样本为男性时，性莂_男等于1，否则为0；再创建一个名为"性莂_女"的哑变量，当该样本为女性时，性莂_女等于1，否则为0。

通过这种方式，我们成功地将性莂这一非数值型变量转换为了适合逻辑回归分析的数值型变量。

5. 哑变量的注意事项在进行逻辑回归分析时，需要注意以下几点：- 避免完全多重共线性：每一个哑变量都应该是完整的，不应该包含多余的信息。

- 避免虚构多重共线性：哑变量要避免陷入虚构多重共线性的误区，即一个哑变量的线性组合不能完全等于另一个哑变量。

- 寻找基准类别：在使用一对多的编码方式时，需要选择一个类别作为基准类别，其他类别相对于该基准类别进行编码，以避免虚构多重共线性的问题。

虚拟变量案例stata
1.定义
引入“虚拟变量（哑变量，dummy variable）”对定性数据或者分类数据，赋值0或者1。

例如，对东部、中部、西部产生虚拟变量，则需要2个。

因为east=1，表示东部；east=0，表示其他地区。

同样middle=1，表示中部；middle=0，表示其他地区。

那么east=0，且middle=0时，则表示west（西部）。

但是值得注意的是，（east=1的个数）+（middle=1的个数）+（表示west的数值）=全体分析样本数。

否则，在stata回归时不会自动检测到多重共线性，自动omit 其中一个变量。

2.设置参照组
下面例子中：east=1，表示东部；middle=1，表示中部；west= 1，表示西部。

目的是为了选择参照组。

"note:west omitted because of collinearity"：我把三个变量都放进去，所以stata检测到多重共线性，把west的变量忽略了，作为参照组（对比组）。

如果想把参照组设定为middle：
reg ln_min edu east west
如果想把参照组设定为east：
reg ln_min edu middle west
或者在回归中指定omit variable：。

逻辑回归的变量类型的处理方法-概述说明以及解释1.引言1.1 概述逻辑回归是一种常用的分类算法，可以用于预测二分类问题。

在应用逻辑回归之前，针对不同类型的变量，我们需要对其进行处理，以确保模型的准确性和可靠性。

本文将详细介绍逻辑回归中变量类型的处理方法。

在进行逻辑回归之前，我们首先需要了解不同变量类型的分类。

变量可以分为两大类：连续变量和离散变量。

连续变量是在一个范围内有无限多个可能值的变量，例如年龄、身高等。

而离散变量则是只有有限个可能值的变量，例如性别、学历等。

针对连续变量，我们通常采取的处理方法是进行归一化或者标准化。

归一化可以将变量的取值范围缩放到0-1之间，而标准化则是将变量的取值转化为均值为0，标准差为1的正态分布。

通过这些处理方法，可以消除不同变量之间的量纲差异，使得模型更加准确。

对于离散变量，我们可以采用编码的方式进行处理。

常见的编码方法有哑变量编码和标签编码。

哑变量编码将原始的离散变量转化为多个二进制变量，用于表示每个可能取值的存在与否。

而标签编码则是将每个取值映射为一个数字。

通过这些编码方法，可以将离散变量转化为模型可以处理的数值。

在本文的接下来的部分，我们将详细介绍连续变量和离散变量的处理方法，并给出具体的示例和实践经验。

同时，我们也会讨论处理不平衡数据和缺失值的相关策略，以提高模型的准确性和稳定性。

总的来说，逻辑回归的变量类型的处理方法对于建立准确可靠的模型至关重要。

通过合理的处理方法，我们可以充分利用各个变量的信息，提高模型的预测能力，为实际问题的解决提供有力的支持。

在接下来的章节中，我们将一一介绍并深入讨论这些处理方法及其应用。

1.2文章结构文章结构部分的内容编写如下：1.2 文章结构本文主要围绕逻辑回归的变量类型展开讨论，在以下章节中将详细介绍不同变量类型的处理方法。

首先，我们将在第2.1节对变量类型进行分类，包括连续变量和离散变量。

随后，在第2.2节中，我们将重点介绍连续变量的处理方法，包括数据标准化、离群值处理和多项式特征构造等。