虚拟变量案例

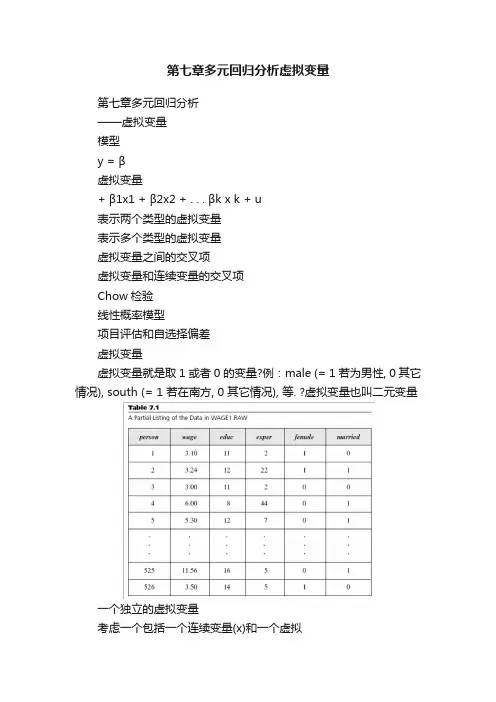
第七章多元回归分析虚拟变量第七章多元回归分析——虚拟变量模型y = β虚拟变量+ β1x1 + β2x2 + . . . βk x k + u表示两个类型的虚拟变量表示多个类型的虚拟变量虚拟变量之间的交叉项虚拟变量和连续变量的交叉项Chow检验线性概率模型项目评估和自选择偏差虚拟变量虚拟变量就是取1 或者0 的变量?例：male (= 1 若为男性, 0 其它情况), south (= 1 若在南方, 0 其它情况), 等. ?虚拟变量也叫二元变量一个独立的虚拟变量考虑一个包括一个连续变量(x)和一个虚拟变量(d)的模型y = β+ δ0d + β1x + u这可以解释成截距项的变化若d = 0, 那么y = β+ β1x + u若d = 1, 那么y = (β+ δ0) + β1x + ud = 0 的样本是参照组δ0 > 0 的例子y y = (β0 + δ0) + β1xd = 1{ δslope = β1d =0 }βy = β0 + β1xx从多个数值的类型变量到虚拟变量?我们可以用虚拟变量来控制有多种类型因素?假设样本中的个人是中学辍学或者仅仅中学毕业或者大学毕业现在要拿仅仅中学毕业和大学毕业的人和中学辍学的人比较定义hsgrad = 1 如果仅仅是中学毕业, 0 其它情况; colgrad = 1 如果大学毕业, 0 其它情况多个数值的类型变量（续）?任何类型变量都可以变成一组虚拟变量?因为参照组由常数项表示了, 那么如果一共有n 个类型，就应该由n –1 虚拟变量如果有太多的类型，通常应该对其进行分组例：前10 , 11 –25, 等虚拟变量之间的交叉项求虚拟变量的交叉项就相当于对样本进行进一步分组例：有男性（male）的虚拟变量和hsgrad（仅仅中学毕业）和colgrad （大学毕业）的虚拟变量加入male*hsgrad 和male*colgrad, 共有五个虚拟变量–> 共有六种类型参照组是女性中学辍学的人此时hsgrad 代表女性仅仅中学毕业者, colgrad 表示女性大学毕业者交叉项表示男性仅仅中学毕业者和男性大学毕业者虚拟变量之间的交叉项（续）?模型可以写成y = β0 + δ1male + δ2hsgrad +δ3colgrad + δ4male*hsgrad + δ5male*colgrad+ β1x + u, 那么:若male = 0 且hsgrad = 0 且colgrad = 0则y = β0 + β1x + u若male = 0 且hsgrad = 1 且colgrad = 0则y = β0 + δ2hsgrad + β1x + u若male = 1且hsgrad = 0且colgrad = 1则y = β0 + δ1male + δ3colgrad + δ5male*colgrad+ βx + u1其它变量与虚拟变量的交叉项?也可以考虑虚拟变量d 和连续变量x 之间的交叉项y = β+ δ1d + β1x + δ2d*x + u若d = 0, 那么y = β+ β1x + u若d = 1, 那么y = (β+ δ1) + (β1+ δ2) x + u这里的两种情况可以看成是斜率的变化δ0 > 0 且δ 1 < 0的例子yy = β+ β1xd = 0d = 1y = (β0 + δ0) + (β 1 + δ1) x。

虚拟变量熵权法-回复虚拟变量与熵权法：解析与应用引言在数据分析与决策过程中，虚拟变量与熵权法是两个常用的工具。

虚拟变量是一种用于表征分类变量的方法，熵权法则是一种基于信息熵的多准则决策方法。

本文将分别介绍虚拟变量与熵权法的原理与应用，并探讨它们在实践中的相互关系。

一、虚拟变量概述1. 什么是虚拟变量？虚拟变量（Dummy Variable），也称为指示变量（Indicator Variable），是一种将分类变量转化为数值变量的方法。

它将一个具有有限个取值的分类变量拆分成多个二值变量（通常取0或1）。

虚拟变量的取值为1表示该样本满足该特征，取值为0表示该样本不具备该特征。

2. 虚拟变量的作用及应用场景虚拟变量的主要作用是将分类变量转化为数值变量，使其能够运用于各类数据分析方法。

虚拟变量广泛应用于统计建模、回归分析、人工智能等领域。

例如，在市场调研中，虚拟变量可以用于探究不同人群的购买行为；在医学研究中，虚拟变量可以用于分析不同药物对疾病治疗效果的影响。

二、虚拟变量的构建方法1. 二元虚拟变量对于具有两个类别的分类变量，可以使用二元虚拟变量。

例如，如果我们要研究一个产品的满意度，可以将分类变量“满意”和“不满意”拆分成两个二元虚拟变量，取值为1表示满意，取值为0表示不满意。

2. 多元虚拟变量对于具有多个类别的分类变量，可以使用多元虚拟变量。

例如，如果我们要研究某地区的消费水平，可以将分类变量“低消费”、“中消费”和“高消费”拆分成三个多元虚拟变量，取值为1表示属于该消费水平，取值为0表示不属于该消费水平。

三、熵权法概述1. 什么是熵权法？熵权法是一种使用信息熵原理进行多准则决策的方法。

它利用信息熵来度量各准则的重要性，根据各准则的权重进行综合评价与决策。

通过熵权法，可以解决多准则决策中的权重确定问题，提高决策的客观性与科学性。

2. 熵权法的应用场景熵权法主要应用于风险评估、投资决策、供应商评估、环境影响评价等领域。

虚拟变量数据的实际例子
1. 想象一下，在研究人们对不同品牌的偏好时，虚拟变量数据就能大显身手啦！比如我们给喜欢品牌 A 的人赋值为 1，不喜欢的赋值为 0，这多直观啊！这就像用信号灯来指示喜好，红灯不喜欢，绿灯喜欢，多简单呀！
2. 嘿，你知道吗？在分析一个地区的气候对农作物的影响时，我们可以用虚拟变量来区分不同季节呀！冬天设为 1，其他季节设为 0，这不就清楚地看
到冬季的特殊之处了吗？这就如同给每个季节贴上了独特的标签一样！
3. 来看看性别对消费行为的影响吧！把男性设为 1，女性设为 0，哇哦，一下子就能看出差异了呢！这好像给男女画上了不同的色彩，让我们能轻易辨别。

4. 当研究人们是否拥有汽车这个因素时，虚拟变量就派上用场啦！有车的是1，没车的是 0，这不是很清晰明了吗？这就跟给每个人身上挂个小牌子似的，一眼就能知道有没有车。

5. 再想想看，在分析不同城市居民的生活方式时，我们可以给大城市设为1，小城市设为 0 呀！这多像是给城市分了个类，一下子就能看出不同的特点啦！
6. 还有啊，研究一个人是否吸烟的时候，用虚拟变量来表示，吸烟为 1，不吸烟为 0，是不是很简单直接呀！这就如同把人分成了两类不同的“阵营”呢！
我的观点结论就是：虚拟变量数据在各种实际情况中都超有用，能让我们快速清晰地了解各种现象背后的关键因素。

虚拟变量（Wooldridge chapter 7 ,13and Gujarati chapter 9）本章所有内容都赋予一个统一的例题来总结：0121234 *** wage female married educ female married female educ married educ ub d d b b b b =+++ ++++ 显然本例是在研究性别、婚姻状况、教育状况同收入之间的 关系问题。

一，单个虚拟变量01 wage female ub d =++ 0 01(|0) (|1) E wage female E wage female b b d == ==+ 也就是说，男性的平均工资为 0 b ，而女性的平均工资为 01 b d + 。

检验 这两组平均工资是否显著不同只需检验 female 是否显著。

如果female 显著且 1ˆ d <0 则说明存在性别歧视。

这也是典型的用虚拟变量 来标志截距的不同。

换成对数——水平形式： 01 log() wage female u b d =++ 则男女之间工资 的百分比差异为： 1 100*[exp()1]d - 以下作一个简单的证明,表明以上公式不仅适用于虚拟变量:111011 101 101 10 1010log() log()log() log(/) / 1 %*100(1)*100 y x u y y y y y y e y y e y y y y e y bb b b b b b =++ -= = = - =- - D ==- 二，双个虚拟变量及其交互012 wage female married ub d d =+++ 02 012 (|0,) (|1,) E wage female married married E wage female married marriedb d b d d ==+ ==++ 因此 1 d 表示在给定婚姻状况条件下， 男女的工资差异。

实验九虚拟变量【实验目的】掌握虚拟变量的设置方法。

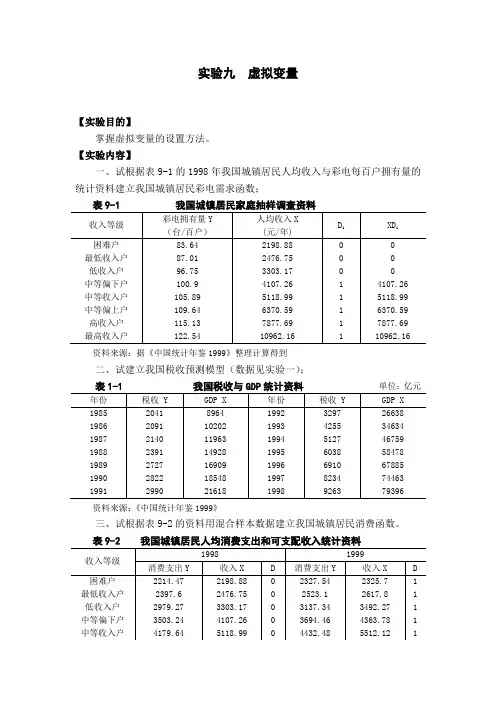
【实验内容】一、试根据表9-1的1998年我国城镇居民人均收入与彩电每百户拥有量的统计资料建立我国城镇居民彩电需求函数；资料来源：据《中国统计年鉴1999》整理计算得到二、试建立我国税收预测模型（数据见实验一）；资料来源：《中国统计年鉴1999》三、试根据表9-2的资料用混合样本数据建立我国城镇居民消费函数。

资料来源：据《中国统计年鉴》1999－2000整理计算得到【实验步骤】一、我国城镇居民彩电需求函数 ⒈相关图分析；键入命令：SCAT X Y ，则人均收入与彩电拥有量的相关图如9-1所示。

从相关图可以看出，前3个样本点（即低收入家庭）与后5个样本点（中、高收入）的拥有量存在较大差异，因此，为了反映“收入层次”这一定性因素的影响，设置虚拟变量如下：⎩⎨⎧=低收入家庭中、高收入家庭1D图9-1 我国城镇居民人均收入与彩电拥有量相关图⒉构造虚拟变量；方式1：使用DATA 命令直接输入； 方式2：使用SMPL 和GENR 命令直接定义。

DATA D1 GENR XD=X*D1 ⒊估计虚拟变量模型： LS Y C X D1 XD再由t 检验值判断虚拟变量的引入方式，并写出各类家庭的需求函数。

按照以上步骤，虚拟变量模型的估计结果如图9-2所示。

图7-2 我国城镇居民彩电需求的估计我国城镇居民彩电需求函数的估计结果为：i i i i XD D x y 0088.08731.310119.061.57ˆ-++==t (16.249)(9.028) (8.320) (-6.593)2R ＝0.9964 2R ＝0.9937 F ＝366.374 S.E ＝1.066虚拟变量的回归系数的t 检验都是显著的，且模型的拟合优度很高，说明我国城镇居民低收入家庭与中高收入家庭对彩电的消费需求，在截距和斜率上都存在着明显差异，所以以加法和乘法方式引入虚拟变量是合理的。

第⼗章虚拟变量第⼗章虚拟变量⼀个例⼦：⼯资⽅程个⼈薪资收⼊（earnings ）受到多种因素的影响，⼈们特别感兴趣的两个主要因素是受教育程度 (years of education) 和⼯作经验（years of experience ）。

为区别这两个因素对⼯资报酬的影响，就需要⼀个多元回归模型。

经济学家在设定⼯资模型时，⼀般认为因变量使⽤⼯资的对数⽐⼯资本⾝更贴近⾼斯—马尔科夫假定。

其模型的⼀个形式为01122ln i i i E y y u βββ=+++其中，E 、1i y 和2i y 分别表⽰⼯资、受教育程度和⼯作经验。

⽤OLS 估计该模型得 01122ln i i E y y βββ∧∧∧∧=++ 1β∧代表⼯作经验相同的情况下，受教育程度（1i y ）对⼯资对数（ln E ∧）的边际影响。

或者理解为受教育年限增加1年，⼯资的百分⽐变化1111(ln )(ln )1d E d E dE dE dE E dy dE dy E dy dy =?==1β∧= 11i y β∧是⼯资对受教育程度的弹性；2β∧代表受教育程度不变的情况下，⼯作经验（2i y ）对⼯资对数(ln E ∧)的边际影响。

通过对⼯资的分析发现，受教育程度和⼯作经验的影响因⼈⽽异。

⼀般认为性别歧视在⼀定程度上是存在的。

性别歧视是否存在？若存在，如何研究男性与⼥性的报酬差异？为此，可以引⼊⼀个特殊的变量对观测对象进⾏分组。

这个特殊的变量就是虚拟变量。

⼀. 虚拟变量的概念虚拟变量（dummy variable ）⼜称为双值变量，取值0或1，⽤以反映观测对象是否具有某种性质或属性，习惯上⽤D 表⽰。

在计量经济模型中引⼊虚拟变量，可以扩展模型的应⽤范围，使模型能更准确反映真实情况。

⼆. 虚拟变量作为⾃变量（⼀）⾃变量中只有虚拟变量性别（i D ）与收⼊（i y ）的关系，可⽤模型i i i y D u αβ=++，i D 是虚拟变量，01i D ?=??m a n w o m a n ()i i E y D ααβαβ=+=+ 01i i D D ==若经过检验，β是显著的，即0β≠，说明性别对收⼊有明显影响。

虚拟变量（dummy variable ）在实际建模过程中，被解释变量不但受定量变量影响，同时还受定性变量影响。

例如需要考虑性别、民族、不同历史时期、季节差异、企业所有制性质不同等因素的影响。

这些因素也应该包括在模型中。

由于定性变量通常表示的是某种特征的有和无，所以量化方法可采用取值为1或0。

这种变量称作虚拟变量，用D 表示。

虚拟变量应用于模型中，对其回归系数的估计与检验方法与定量变量相同。

1． 截距移动 设有模型，y t = β0 + β1 x t + β2D + u t ,其中y t ，x t 为定量变量；D 为定性变量。

当D = 0 或1时，上述模型可表达为，β0 + β1x t + u t , (D = 0) y t = (β0 + β2) + β1x t + u t , (D = 1)0204060204060X Y图8.1 测量截距不同D = 1或0表示某种特征的有无。

反映在数学上是截距不同的两个函数。

若β2显著不为零，说明截距不同；若β2为零，说明这种分类无显著性差异。

例：中国成年人体重y （kg ）与身高x （cm ）的回归关系如下： –105 + x D = 1 (男)y = - 100 + x - 5D =– 100 + x D = 0 (女) 注意：① 若定性变量含有m 个类别，应引入m -1个虚拟变量，否则会导致多重共线性，称作虚拟变量陷阱（dummy variable trap ）。

② 关于定性变量中的哪个类别取0，哪个类别取1，是任意的，不影响检验结果。

③ 定性变量中取值为0所对应的类别称作基础类别（base category ）。

④ 对于多于两个类别的定性变量可采用设一个虚拟变量而对不同类别采取赋值不同的方法处理。

如：1 (大学) D = 0 (中学) -1 (小学)。

β0β0+β2D = 1 D =0【案例1】 中国季节GDP 数据的拟合（虚拟变量应用，file ：case1及case1-solve ）1.21.62.02.42.896:196:397:197:398:198:399:199:300:100:3GDP1.01.52.02.53.00510152025TGD PGDP 序列图 不用虚拟变量的情形若不采用虚拟变量，得回归结果如下，GDP = 1.5427 + 0.0405 T(11.0) (3.5) R 2 = 0.3991, DW = 2.6, s.e. = 0.3 定义1 （1季度） 1 （2季度） 1 （3季度） D 1 = D2 = D3 =0 （2, 3,4季度） 0 （1, 3, 4季度） 0 （1, 2, 4季度）第4季度为基础类别。

虚拟变量案例stata
1.定义
引入“虚拟变量（哑变量，dummy variable）”对定性数据或者分类数据，赋值0或者1。

例如，对东部、中部、西部产生虚拟变量，则需要2个。

因为east=1，表示东部；east=0，表示其他地区。

同样middle=1，表示中部；middle=0，表示其他地区。

那么east=0，且middle=0时，则表示west（西部）。

但是值得注意的是，（east=1的个数）+（middle=1的个数）+（表示west的数值）=全体分析样本数。

否则，在stata回归时不会自动检测到多重共线性，自动omit 其中一个变量。

2.设置参照组
下面例子中：east=1，表示东部；middle=1，表示中部；west= 1，表示西部。

目的是为了选择参照组。

"note:west omitted because of collinearity"：我把三个变量都放进去，所以stata检测到多重共线性，把west的变量忽略了，作为参照组（对比组）。

如果想把参照组设定为middle：
reg ln_min edu east west
如果想把参照组设定为east：
reg ln_min edu middle west
或者在回归中指定omit variable：。