欧拉路径和欧拉回路PPT学习课件
- 格式:ppt
- 大小:509.00 KB
- 文档页数:40

欧拉图中欧拉回路的算法,演示,及分析
设G为欧拉图,一般来说G中存在若干条欧拉回路,下面介绍两种求欧拉回路的算法。
1.Fleury算法,能不走桥就不走桥:
(1)任取v0∈V(G),令P0=v0.
(2)设Pi=v0e1v1e2…e i v i已经行遍,按下面方法来从E(G)-{e1,e2,…,e i}中选取e i+1:
(a)e i+1与v i相关联;
(b)除非无别的边可供行遍,否则e i+1不应该为G i=G-{e1,e2,…,e i}中的桥。
(3)当(2)不能再进行时,算法停止。
可以证明,当算法停止时所得简单回路P m=v0e1v1e2…e m v m(v m=v0)为G中一条欧拉回路。
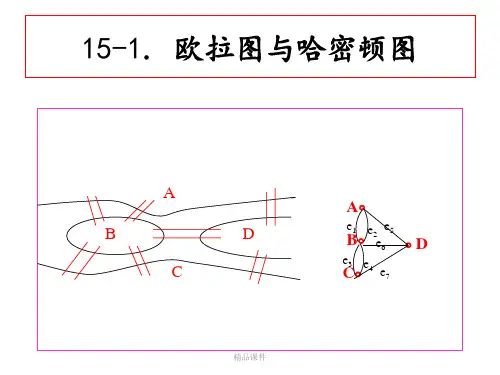
例15.2 图15.4(1)是给定的欧拉图G。
某人用Fleury算法求G中的欧拉回路时,走了简单回路v2e2v3e3v4e14v9e10v2e1v1e8v8e9v2之后(观看他的错误走法),无法行遍了,试分析在哪步他犯了错误?
解此人行遍v8时犯了能不走桥就不走桥的错误,因而他没行遍出欧拉回路。
当他走到v8时,G-{e2,e3,e14,e10,e1,e8}为图15.4(2)所示。
此时e9为该图中的桥,而e7,e11均不是桥,他不应该走e9,而应该走e7或e11,他没有走,所以犯了错误。
注意,此人在行遍中,在v3遇到过桥e3,v1处遇到过桥e8,但当时除桥外他无别的边可走,所以当时均走了桥,这是不会犯错误的。





欧拉回路定理
欧拉回路定理是图论中的一个重要定理,它描述了图中存在欧拉回路的条件。
具体来说,对于无向图来说,该定理表明:图G存在欧拉通路的充要条件是:G为连通图,并且G仅有两个奇度结点(度数为奇数的顶点)或者无奇度结点;图G存在欧拉回路的充要条件是:G为连通图,并且所有结点的度数均为偶数。
对于有向图来说,该定理表明:图D存在欧拉通路的充要条件是:D为有向图,D的基图连通,并且所有顶点的出度与入度都相等;或者除两个顶点外,其余顶点的出度与入度都相等,而这两个顶点中一个顶点的出度与入度之差为1,另一个顶点的出度与入度之差为-1;图D存在欧拉回路的充要条件是:D为连通图,且所有顶点的出度与入度都相等。


欧拉路径和欧拉回路概念欧拉路径:图&G&中的⼀条路径若包括每个边恰好⼀次,则其为欧拉路径欧拉回路:⼀条回路如果是欧拉路径,那么其为欧拉回路存在条件⽆论⽆向图还是有向图,⾸要条件为所有边都是连通的⽆向图1. 存在欧拉路径的充要条件:度数为奇数的点只能有0或2个2. 存在欧拉回路的充要条件:度数为奇数的点只能有0个有向图1. 存在欧拉路径的充要条件:所有点出度=⼊度;或除两点外其余所有点出度=⼊度,余下两点⼀个出度-⼊度=1(地点),另⼀个⼊度-出度=1(终点)2. 存在欧拉回路的充要条件:所有点出度=⼊度注:欧拉回路为欧拉路径的⼀种特例,因此如果说存在欧拉路径是包含存在欧拉回路这种情况的算法流程1. 建图并统计点的度数(有向图分⼊度和出度)2. 根据度数进⾏初步的有解性判定如何理解"初步":所有点的度数均满⾜要求不等价于所有边均连通。
连通性判定在此处⽆法解决,因此为初步的合法性判定⽆向图统计度数为奇数的点个数count欧拉回路:count == 0欧拉路径:count == 0 || count == 2有向图欧拉回路:有解仅需保证所有点⼊度==出度即可欧拉路径:设din[i]为i点的⼊度,dout[i]为i点的出度dout[i] - din[i] == 1的点数为startNum(满⾜起点特征)din[i] - dout[i] == 1的点数为endNum(满⾜终点特征)success表⽰是否有解⽅法1:for (int i = 1; i <= n; ++i) // 枚举所有点if (din[i] != dout[i]){if (dout[i] - din[i] == 1) ++ startNum;else if (din[i] - dout[i] == 1) ++endNum;else success = false;}有解的条件为success && (!startNum && !endNum || startNum == 1 && endNum == 1)⽐较容易理解的是success为false时⼀定是⽆解的不容易理解的是,success为true时不⼀定是有解的,因为最多只能有2个点的出度!=⼊度,⽽success为true并不能保证这⼀点⽅法2:设count为出度!=⼊度的点个数,flag为出度!=⼊度点的(出度-⼊度)的乘积(或者⼊度-出度的乘积)for (int i = 1; i <= n; ++i) // 枚举所有点if (din[i] != dout[i]){++count;flag *= dout[i] - din[i];}有解的条件为!count || (count == 2 && flag == -1)即出度!=⼊度的点数为0 或出度 != ⼊度的点数为2并且对应两个点,起点满⾜dout[i] - din[i] == 1, 终点满⾜dout[i] - din[i] == -1注:如果题⽬保证⾄少存在⼀组解,则此判定过程可以省略3. 选取起点⾸先需要明确两点1. 从欧拉回路上任意⼀点dfs均可搜索到其所在的欧拉回路2. 从欧拉路径上任意⼀点dfs未必可以搜索到其所有的欧拉路径,必须从满⾜⼀定性质的点出发才可原因很简单,对于⼀个环路来说,从任意⼀点开始都可以⼀笔画出整个环;对于⼀个路径,只有从起点开始才可以⼀笔画出整条路径欧拉回路:如果题⽬要求的为欧拉回路,在⽆向图中,满⾜所有点的度数为偶数,在有向图中,满⾜所有点的出度==⼊度,所有点都是等价的,因此dfs的起点只需定为⼀个⾮孤⽴点为何⼀定是⾮孤⽴点: 在此类题⽬中,⼀般不能保证点是连通的,因此是存在孤⽴点的,但是孤⽴点的存在对欧拉回路或路径的存在并不产⽣影响,但是如果从孤⽴点开始是找不到回路或路径的欧拉路径:如果题⽬要求的为欧拉路径,对于⽆向图,需要找到度数为奇数的点作为起点,对于有向图,需要找到dout[i] - din[i] == 1的点i 4.从起点开始dfs寻找欧拉回路或欧拉路径欧拉回路和欧拉路径问题的本质是边的问题,类⽐对点的dfs问题,我们同样需要对⾛过的边进⾏标记,防⽌重复void dfs(int u){for (int i = h[u]; ~i; i = ne[i]){if (st[i]) continue; // 对⾛过的边进⾏标记st[i] = true;dfs(e[i]);res[++cnt] = i;}}dfs部分难点-递归搜索和存储答案的顺序问题dfs(e[i]);res[++cnt] = i;在常规dfs中,搜索到某个点会⾸先把该点进⾏存储,然后再递归搜索,但是求解欧拉路径需要递归搜索完⼀个节点后再把到该节点的边进⾏存储为了说明这两种顺序产⽣的不同结果,以⼀组数据为例/*** ⽆向图* 5个点,6条边* 以下6⾏a b表⽰:a与b之间有⼀条边*/5 62 32 53 41 24 25 1对边进⾏存储,如果采取先存储再搜索的顺序,结果为4 2 6 1 3 5如果采取先搜索再存储的顺序,结果为6 2 5 3 1 4可以发现,第⼆种顺序得到的恰好是欧拉路径的倒序,结果只需要倒序输出即可dfs部分难点-优化问题最终的优化⽅案实际分为两个部分,为了更加透彻理解优化原理,逐层进⾏分析1. 原始思路void dfs(int u){for (int i = h[u]; ~i; i = ne[i]){if (st[i]) continue; // 对⾛过的边进⾏标记st[i] = true;// 如果为⽆向图,这⾥还需要对反向边进⾏标记dfs(e[i]);res[++cnt] = i;}}上述代码为⼀般思路,存在的问题为⾛过的边存在重复枚举。
