y n 1 y n f (x n, y n), x x n 1 n
即
y y hf ( x , y ) n 1 n n n
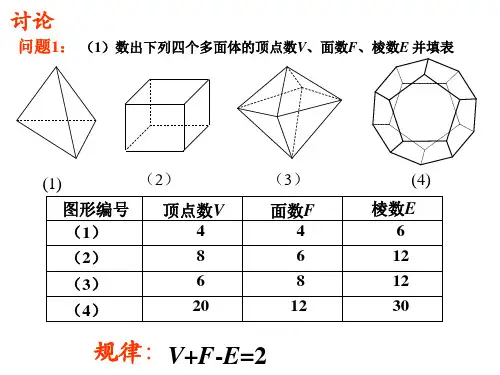
《离散数学》中的欧拉公式: 若G为连通平面图,则n-m+r=2,其中,n,m,r分别 为G的结点数,边数和面数。
另外,我们在《常微分方程》中还学了欧拉折
线;在《离散数学》中 学过欧拉图。
认识欧拉
欧拉---瑞士人(Euler,L. 1707---1783);
欧拉---16 岁获得硕士学位;
欧拉---数学史上“高产”的数学家。在世发表论文700多篇,
去世后还留下100多篇待发表;
欧拉---首先使用f(x)表示函数,用e表示自然对数的底,用a、
b、c 表示△ABC,用∑表示求和,用i表示虚数单位等。
欧拉公式的两个基本性质
o s is in i c o s 1 i s i n 1 e c 1、 e 2 2 3 i i 3 3 2 e c o s i s i n 1e c o s is i n i 2 2
i
i 2
2 k i e c o s 2 k i s i n 2 k 1 k 0 , 1 , 2
dz d iz
5、 倍角和半角的三角变换 例:证明: sin 2 cot
1 co s 2
证:左
e2i e2i i e2i e2i
e2i e2i sin2 2i e2i e2i 1 cos2 1 2
i i i i i i 1 e e e e ie e i 2 i i i e e ie e