机器人静力学和雅克比实验

并联机器人的雅可比，可操作性，条件数和精度（翻译论文）虽然在最早的机器人研究中就已经有了雅可比矩阵的概念、可操纵性、条件数的概念，但是它们的真正意义并不是很好理解。

在本文中，我们重新审视这些作为并联机器人优化设计精度指标的概念。

首先，我们指出，通常的雅可比矩阵的输入—输入方程可能不足以分析平台的定位误差。

然后我们检验可操纵性的概念，表明其经典的解释是错误的。

我们考虑各种常见的局部灵巧指数，其中大部分是基于雅可比矩阵的条件数。

值得注意的是，即使对于一个给定的机器人，在一个特定的姿态也会有各种各样的条件数，这些条件数之间都不一致，和我们想得到的精度指标也不一致。

然后考虑了全局调节指数。

除了存在基于错误的局部准确性指数的问题外，还有一个忽略了大部分时间而进行计算的计算问题。

最后，我们检验了其他哪些指标可用于优化设计，并且介绍了计算它们的难度。

1 引言我们将使用一个相对通用的非冗余并联机构的定义。

当一个机构用至少两个运动链来控制自由度n<6的末端执行器时，我们定义它为并联机构，而其他的6-n 个自由度是一个恒定值通过单自由度驱动关节控制。

此外，如果将驱动器锁定，则末端执行器的自由度为0，非驱动关节有一个单自由度。

这样的定义涵盖了经典的六自由度机器人，比如Gough 和Hexa 平台，还有少于六自由度的机构，如Delta 和3-UPU 机构。

如今，并联机构的应用领域越来越广，如望远镜、精定位装置、包装速度快、机床、医疗。

对尺寸非常的敏感是并联机构优化设计的一个关键问题。

最优设计的方法有静力学性能指标。

精度显然是许多应用中的一个关键问题。

并联机构也有串联机构的一些关键问题，因此，针对这些问题做了很多广泛的研究，定义除了很多准确性指标，这些结果已经应用到并联机构上。

本文的目的是检验这些指标是否适用于并联机构。

雅可比矩阵和逆雅可比矩阵用于研究末端执行器的定位精度的，为了这个目的，很有必要研究它们的概念。

并联机器人的雅可比，可操作性，条件数和精度（翻译论文）虽然在最早的机器人研究中就已经有了雅可比矩阵的概念、可操纵性、条件数的概念，但是它们的真正意义并不是很好理解。

在本文中，我们重新审视这些作为并联机器人优化设计精度指标的概念。

首先，我们指出，通常的雅可比矩阵的输入—输入方程可能不足以分析平台的定位误差。

然后我们检验可操纵性的概念，表明其经典的解释是错误的。

我们考虑各种常见的局部灵巧指数，其中大部分是基于雅可比矩阵的条件数。

值得注意的是，即使对于一个给定的机器人，在一个特定的姿态也会有各种各样的条件数，这些条件数之间都不一致，和我们想得到的精度指标也不一致。

然后考虑了全局调节指数。

除了存在基于错误的局部准确性指数的问题外，还有一个忽略了大部分时间而进行计算的计算问题。

最后，我们检验了其他哪些指标可用于优化设计，并且介绍了计算它们的难度。

1 引言我们将使用一个相对通用的非冗余并联机构的定义。

当一个机构用至少两个运动链来控制自由度n<6的末端执行器时，我们定义它为并联机构，而其他的6-n 个自由度是一个恒定值通过单自由度驱动关节控制。

此外，如果将驱动器锁定，则末端执行器的自由度为0，非驱动关节有一个单自由度。

这样的定义涵盖了经典的六自由度机器人，比如Gough 和Hexa 平台，还有少于六自由度的机构，如Delta 和3-UPU 机构。

如今，并联机构的应用领域越来越广，如望远镜、精定位装置、包装速度快、机床、医疗。

对尺寸非常的敏感是并联机构优化设计的一个关键问题。

最优设计的方法有静力学性能指标。

精度显然是许多应用中的一个关键问题。

并联机构也有串联机构的一些关键问题，因此，针对这些问题做了很多广泛的研究，定义除了很多准确性指标，这些结果已经应用到并联机构上。

本文的目的是检验这些指标是否适用于并联机构。

雅可比矩阵和逆雅可比矩阵用于研究末端执行器的定位精度的，为了这个目的，很有必要研究它们的概念。

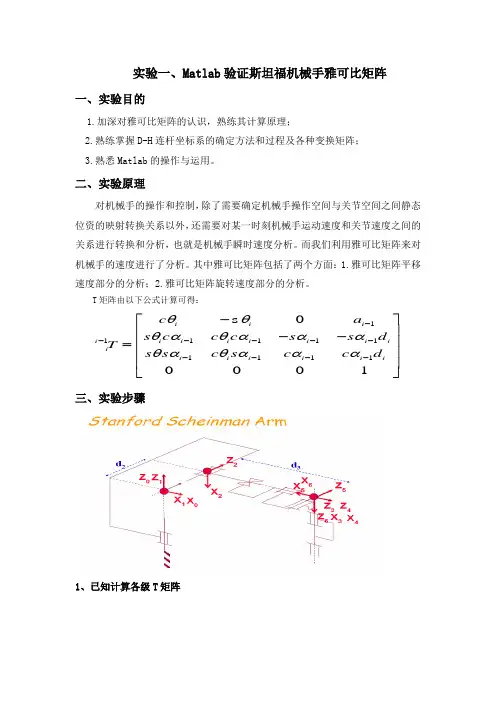
实验一、Matlab 验证斯坦福机械手雅可比矩阵 一、实验目的1.加深对雅可比矩阵的认识，熟练其计算原理；2.熟练掌握D-H 连杆坐标系的确定方法和过程及各种变换矩阵；3.熟悉Matlab 的操作与运用。

二、实验原理对机械手的操作和控制，除了需要确定机械手操作空间与关节空间之间静态位资的映射转换关系以外，还需要对某一时刻机械手运动速度和关节速度之间的关系进行转换和分析，也就是机械手瞬时速度分析。

而我们利用雅可比矩阵来对机械手的速度进行了分析。

其中雅可比矩阵包括了两个方面：1.雅可比矩阵平移速度部分的分析；2.雅可比矩阵旋转速度部分的分析。

T 矩阵由以下公式计算可得：1111111111s 0001iii i i i i i i i i ii i i i i i c a s c c c s s d T s s c s c c d θθθαθαααθαθααα-----------⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥⎣⎦三、实验步骤1、已知计算各级T 矩阵665544445436546655221132210321220000000010001000000000100001000100011000000000100101000001001---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦--⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥===⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦-c s c s c s s c T T T s c s c c s c s d d T T T s c 1100001001⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦s c 2、计算出各连杆坐标系到基坐标系0的变换矩阵：11110111212112112121121022221211213212121121321203222000000001010010000000100-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦----⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥==⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦---+++=-可知可知c s s c T z c c c s s s d s s c s s c c d c T z s c c c s c s c d s s d s c c s s s d s c d T s c c d 12123320010⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦可知c s s s z c 1241412414121231212414124141212312042424223124141251241451251241412312124145050001()()()----⎡⎤⎢⎥+-++⎢⎥=⎢⎥-⎢⎥⎣⎦--------+-=++c c c s s c c s s c c s c s d s d s c c c s s c s c c s s s s d c d T s c s s c c d c c c s s c s s c c c s s s c s c c c s s c c s d s d s c c c s c s T 12512414512512414123122423124514512512312124514512512312062455223()2452524525000112345600⎡⎤⎢⎥-+--+--+++⎢⎥⎢⎥-⎢⎥⎣⎦-+-++++=-s s s c c c s s s s c s c s c c s s d c d s c c c s s c s c c s s c d X X c c c s s s s c s c c s d s d X X s c c s c s s s s c s s d c d T X X s c s c c c d 01⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦Matlab 计算过程如下：>> clear>> syms c1 s1 c2 s2 c3 s3 c4 s4 c5 s5 c6 s6 d1 d2 d3 d4 d5 d6 a1 a2 a3 a4 a5 a6>> T10=[c1 -s1 0 0;s1 c1 0 0;0 0 1 0;0 0 0 1]>> T21=[c2 -s2 0 0;0 0 1 d2;-s2 -c2 0 0;0 0 0 1] >> T32=[1 0 0 0;0 0 -1 -d3;0 1 0 0;0 0 0 1] >> T43=[c4 -s4 0 0;s4 c4 0 0;0 0 1 0;0 0 0 1] >> T54=[c5 -s5 0 0;0 0 1 0; -s5 -c5 0 0;0 0 0 1] >> T65=[c6 -s6 0 0;0 0 -1 0;s6 c6 0 0;0 0 0 1]>> T20=T10*T21； >> T30=T20*T32； >> T40=T30*T43； >> T50=T40*T54； >> T60=T50*T65；>> T60=simplify(T60)3、用速度矢量合成的方法计算雅可比矩阵Jv 部分：356124123456102040506016263465666124561020162631245600000⎡⎤=⎢⎥⎢⎥⎣⎦⎡⎤⨯⨯⨯⨯⨯=⎢⎥⎣⎦⎡⎤⨯⨯=⎢⎥⎣⎦v v v v v v J J J J J J J J J J J J J z p z p z z p z p z p z z z z z z p z p z z z z z z ωωωωωω 1） 计算1016⨯z p1z 为连杆1坐标系的z 轴单位向量在基坐标系0中的描述；16p 为连杆1坐标系原点到连杆6坐标系原点连线矢量16O O，在基坐标系0中的描述，计算过程为：计算矩阵T61，T61的第四列即为16O O，由于坐标系1相对于坐标系0有绕Z 轴的转动，故需要对其进行转换，转换方法为；0116O O ⋅ R ，01R为T10中旋转部分注：Matlab 中向量叉积方法：e=cross (a,b)>> T61=T21*T32*T43*T54*T65 %计算出16O O在坐标系1中的描述>> P161=[s2*d3;d2;c2*d3]>> Rot10=[c1 -s1 0;s1 c1 0;0 0 1] %由T10知道旋转部分变换3*3矩阵 >> P160= Rot10* P161 % 与P60最后一列比较 >> z1=[0;0;1]>> e=cross(z1,P160) %可得到Jv 第一列： e =[ -s1*s2*d3-c1*d2; c1*s2*d3-s1*d2;0]2） 计算2026⨯z p2z 为连杆2坐标系的z 轴单位向量在基坐标系0中的描述；206p 为连杆2坐标系原点到连杆6坐标系原点连线矢量26O O，在基坐标系0中的描述，计算过程为：计算矩阵P62，P62的第四列即为26O O，由于坐标系2相对于坐标系0有姿态变化，故需要对其进行转换，转换方法为；0226O O ⋅ R ，02R为T20中旋转部分注：Matlab 中向量叉积方法：e=cross (a,b)>> T62= T32*T43*T54*T65 %计算出26O O在坐标系2中的描述>> P262=[0;-d3;0]>> Rot20=[c1*c2 -c1*s2 -s1;s1*c2 -s1*s2 c1;-s2 -c2 0] %由T20知旋转部分变换3*3矩阵>> P260= Rot20* P262 >> z2=[-s1;c1;0]>> e=cross(z2, P260) %可得到Jv 第一列：e =[c1*c2*d3; s1*c2*d3; -s1^2*s2*d3-c1^2*s2*d3]3） 由于连杆3坐标系为移动坐标系，故起对连杆6的速度贡献不能计算为3036⨯z p ，而应该为Z3的单位向量在基坐标系0中的表示；故由T30直接可得Jv 第三列为：1212320⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦c s s s z c4)由于坐标系4、5、6和坐标系6的坐标原点重合故对应6066)=⨯=⨯ i i ()q(q i i O i i i v z O O z p 的计算结果均为0 ，于是可得 35612412345612123123121212312312232112414124141245145125112414124141245000000000000⎡⎤=⎢⎥⎢⎥⎣⎦---+-=------+-+-++v v v v v v J J J J J J J J J J J J J c d s s d c c d c s s d c s d s c d s s s d c s c c s s c c c s s c c c c s s s s c s c c s c s c c s c s c c s c c s c ωωωωωω14512524242455210⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥-+⎢⎥⎣⎦s s s s c s s s s s c s c c 5) 用直接求导的方法验证上面Jv 的计算的正确性：在matlab 中用B=jacobian(f,v)方法直接求导可以获取雅可比矩阵四、实验总结机器人雅可比矩阵能够很好地反映出操作空间与关节空间的速度映射关系，而Matlab 则很好的简化了这种关系求导手段。

雅可比矩阵在机器人静力学中的作用雅可比矩阵在机器人静力学中扮演了关键的角色，它用于描述机器人系统中的运动学和动力学关系。

下面我将逐个回答你的问题，并用易于理解的术语解释。

1. 雅可比矩阵是什么雅可比矩阵是一个将机器人的关节速度与其末端执行器速度之间的关系进行描述的矩阵。

它将机器人关节空间中的速度转化为末端执行器空间中的速度。

雅可比矩阵的每个元素代表了末端执行器速度对于关节速度的敏感程度。

2. 机器人的静力学是什么机器人的静力学研究的是机器人系统在静止或匀速运动时所受到的力学影响。

它关注的是机器人系统在特定关节角度下的受力情况，包括关节力和末端执行器力等。

3. 雅可比矩阵在机器人静力学中的作用是什么雅可比矩阵在机器人静力学中的作用是用于分析机器人系统中的力学平衡和力的传递。

通过雅可比矩阵，我们可以将末端执行器的力转化为关节力，并且可以控制机器人系统中的力分配。

4. 如何利用雅可比矩阵进行力的传递分析在机器人静力学中，我们可以利用雅可比矩阵来分析力的传递和分布。

具体而言，我们可以通过雅可比矩阵将末端执行器上的力转化为关节空间中的力。

这样，我们可以对机器人系统进行力分析，包括力矩的计算和力的传递路径的分析等。

5. 为何需要力的传递分析力的传递分析对于机器人的应用非常重要。

它可以帮助我们理解机器人系统中的力分配情况，从而进行力控制和路径规划等。

通过力的传递分析，我们可以确定机器人系统中各个部分所受到的力，以及力的传递路径是否满足设计要求。

总结起来，雅可比矩阵在机器人静力学中的作用是描述机器人系统中的运动学和动力学关系。

它帮助我们分析机器人系统中的力学平衡和力的传递，从而进行力控制和路径规划等。

通过雅可比矩阵的应用，我们可以将末端执行器的力转化为关节力，并且可以确定机器人系统中各个部分所受到的力，从而进行力的传递分析。

这对于机器人的应用非常重要，能够帮助我们优化机器人的设计和控制，提高其性能和安全性。

scara机器人运动学方程雅可比矩阵
Scara机器人是一种广泛应用于工业领域的机器人，它的运动学方程雅可比矩阵是描述其运动学性能的重要工具。

通过雅可比矩阵，我们可以了解到Scara机器人在不同关节位置和速度下的末端执行器的速度和位置关系。

雅可比矩阵是一个2x3的矩阵，其中的元素代表了末端执行器位置和速度相对于关节角度和速度的变化率。

简单来说，雅可比矩阵可以帮助我们理解Scara机器人的动力学特性和运动规律。

通过对雅可比矩阵的分析，我们可以得到一些有用的信息。

首先，我们可以确定Scara机器人的工作空间范围，即机器人可以到达的位置和姿态。

其次，我们可以根据雅可比矩阵来计算机器人在不同关节角速度下的末端执行器速度，从而实现机器人的精确控制。

除此之外，雅可比矩阵还可以用于路径规划和碰撞检测。

通过计算机器人在不同关节位置下的雅可比矩阵，我们可以确定机器人在执行任务过程中是否会发生碰撞，从而避免潜在的安全风险。

Scara机器人的运动学方程雅可比矩阵是研究机器人运动学行为和控制的重要工具。

通过对雅可比矩阵的研究和分析，我们可以深入理解机器人的运动规律，并实现对机器人的精确控制和路径规划。

机器人实验报告学院：专业：姓名：学号：教师：日期：实验一一．实验目的：1.对斯坦福6自由度机械手相邻连杆D-H矩阵的构建以及每一个连杆的坐标系的构建进行详细叙述和说明，并对每一对相邻连杆的4个D-H参数进行详细说明；2.对RRRR机械手受力分析的Matlab验证过程进行详细说明，并构建相邻连杆的D-H坐标系，列表说明每一对相邻连杆的D-H参数3.对斯坦福机械手逆向运动分析中seta1的求解进行简化并和教材计算结果进行对比4.阐述齐次变换矩阵变换方法在斯坦福机械手中应用，加上自己的理解进行文字叙述二．对RRRR机械手受力分析的Matlab验证过程进行详细说明，并构建相邻连杆的D-H坐标系，列表说明每一对相邻连杆的D-H参数分析下图RRRR 机械手其正向变换矩阵和转动雅可比矩阵如下(a)求解当各个关节坐标为q = [0, 900,−900, 0] T 的时候，相对于基坐标系的雅可比矩阵 Jo(b) 一个作用在坐标系 {4} 上的力 [0, 6, 0, 7, 0, 8]T . 在 (a)中所描述的位置, 计算用于平衡的关节力矩>> syms theta1 theta2 theta3 theta4 >>F=[(2^0.5)*cos(theta1+theta2)*cos(theta3)-sin(theta1+theta2)*(sin(theta3)-1)+cos(theta1);...(2^0.5)*sin(theta1+theta2)*cos(theta3)+cos(theta1+theta2)*(sin(theta3)-1)+sin(theta1);... sin(theta3)+1]>> V=[theta1;theta2 ;theta3 ;theta4]>> Jv=jacobian(F,V)4(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)((90)1)(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)(90)((90)1)(90)(90)(c c s c s c c s s c s c s s s c c c s s T ---------+------+--+=-90)(90)1001s ⎛⎫⎪⎪ ⎪⎪⎪ ⎪--+⎪⎪ ⎪⎝⎭402220101002201T ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭>> Jv01=subs(Jv,theta1,0)>> Jv01=subs(Jv01,theta2, 1.5707953) %1.5707953 为90度的弧度表示>> Jv01 =subs(Jv01,theta3,- 1.5707953)>> Jv01 =subs(Jv01,theta4,0)>> Jw=[0 0 (2^0.5)/2 (2^0.5)/2;0 0 0 0;1 1 (2^0.5)/2 (2^0.5)/2]>> Jac=[Jv01;Jw]>> R40=[(2^0.5)/2 0 (2^0.5)/2;0 1 0;-(2^0.5)/2 0 (2^0.5)/2]>> E0=[0 0 0;0 0 0;0 0 0]>> R40ZG=[R40 E0;E0 R40]>> F40=R40ZG*[0;-6;0;-7;0;-8]>> Tao=Jac'*F40Tao =-18.5701-12.5701-15.9863-8.0000三．对斯坦福机械手逆向运动分析中seta1的求解进行简化并和教材计算结果进行对比逆向运动学分析示例：>> syms c1 s1 c2 s2 d3 c4 s4 c5 s5 c6 s6 d2>> T10=[c1 -s1 0 0;s1 c1 0 0;0 0 1 0;0 0 0 1]>> T21=[c2 -s2 0 0;0 0 1 d2;-s2 -c2 0 0;0 0 0 1]>> T32=[1 0 0 0;0 0 -1 -d3;0 1 0 0;0 0 0 1]>> T43=[c4 -s4 0 0;s4 c4 0 0;0 0 1 0;0 0 0 1]>> T54=[c5 -s5 0 0;0 0 1 0; -s5 -c5 0 0;0 0 0 1]>> T65=[c6 -s6 0 0;0 0 -1 0;s6 c6 0 0;0 0 0 1]>> T60=T10*T21*T32*T43*T54*T65>> T10nizhen=inv(T10)>> T21nizhen=inv(T21)>> T32nizhen=inv(T32)>> T43nizhen=inv(T43)>> T54nizhen=inv(T54)>> T65nizhen=inv(T65)>> syms nx ox ax px ny oy ay py nz oz az pz>> T60yizhi=[nx ox ax px;ny oy ay py;nz oz az pz;0 0 0 1]下面计算：1）T10nizhen*T60yizhi=T21*T32*T43*T54*T652）T21nizhen*T10nizhen*T60yizhi = T32*T43*T54*T653）T32nizhen*T21nizhen *T10nizhen* T60yizhi= T43*T54*T654）T43nizhen*T32nizhen *T21nizhen *T10nizhen* T60yizhi= T54*T65 5）T54nizhen*T43nizhen* T32nizhen *T21nizhen *T10nizhen* T60yizhi= T651）对比矩阵两边第二行第四列有-s1/(c1^2+s1^2)*px+c1/(c1^2+s1^2)*py= d2 >> syms st1 st2 st3 st4 st5 st6 d2 d3>> [x]=solve('-sin(st1)*px+cos(st1)*py=d2','st1') Simplify()四．MTLAB 验证斯坦福雅可比矩阵 1．已知计算各级T 矩阵 由公式：1111111111s 0001i i i i i i i i i ii ii i i i i i c a s c c c s s d T s s c s c c d θθθαθαααθαθααα-----------⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥⎣⎦以及各连杆坐标系之间的参数表，可得：665544445436546655221132210321220000000010001000000000100001000100011000000000100101000000101---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦--⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥===⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦-c s c s c s s c T T T s c s c c s c s d d T T T s c 1100001001⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦s c与斯坦福大学开发课件比较发现其课件中T21计算有错：2．计算出各连杆坐标系到基坐标系0的变换矩阵：11110111212112112121121022221211213212121121321203222000000001010010000000100-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦----⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥==⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦---+++=-可知可知c s s c T z c c c s s s d s s c s s c c d c T z s c c c s c s c d s s d s c c s s s d s c d T s c c d 1212332010⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦可知c s s s z c124141241412123121241412414121231204242422312414125124145125124141231212414505001()()()----⎡⎤⎢⎥+-++⎢⎥=⎢⎥-⎢⎥⎣⎦--------+-=++c c c s s c c s s c c s c s d s d s c c c s s c s c c s s s s d c d T s c s s c c d c c c s s c s s c c c s s s c s c c c s s c c s d s d s c c c s c s T 12512414512512414123122423124514512512312124514512512312062455223()24525245250011234560⎡⎤⎢⎥-+--+--+++⎢⎥⎢⎥-⎢⎥⎣⎦-+-++++=-s s s c c c s s s s c s c s c c s s d c d s c c c s s c s c c s s c d X X c c c s s s s c s c c s d s d X X s c c s c s s s s c s s d c d T X X s c s c c c d 01⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦与斯坦福开发课程课件比较Matlab 计算过程如下： >> clear>> syms c1 s1 c2 s2 c3 s3 c4 s4 c5 s5 c6 s6 d1 d2 d3 d4 d5 d6 a1 a2 a3a4 a5 a6>> T10=[c1 -s1 0 0;s1 c1 0 0;0 0 1 0;0 0 0 1] >> T21=[c2 -s2 0 0;0 0 1 d2;-s2 -c2 0 0;0 0 0 1] >> T32=[1 0 0 0;0 0 -1 -d3;0 1 0 0;0 0 0 1] >> T43=[c4 -s4 0 0;s4 c4 0 0;0 0 1 0;0 0 0 1] >> T54=[c5 -s5 0 0;0 0 1 0; -s5 -c5 0 0;0 0 0 1] >> T65=[c6 -s6 0 0;0 0 -1 0;s6 c6 0 0;0 0 0 1] >> T20=T10*T21 >> T30=T20*T32 >> T40=T30*T43 >> T50=T40*T54 >> T60=T50*T65可以用simplify 函数简化，如： >> T60=simplify(T60)3．用速度矢量合成的方法计算雅可比矩阵Jv 部分：356124123456102450601626346566612456102162631245600000⎡⎤=⎢⎥⎢⎥⎣⎦⎡⎤⨯⨯⨯⨯⨯=⎢⎥⎣⎦⎡⎤⨯⨯=⎢⎥⎣⎦v v v v v v J J J J J J J J J J J J J z p z p z z p z p z p z z z z z z p z p z z z z z z ωωωωωω（1）.计算1016⨯zp1z 为连杆1坐标系的z 轴单位向量在基坐标系0中的描述；106p为连杆1坐标系原点到连杆6坐标系原点连线矢量16O O，在基坐标系0中的描述，计算过程为：计算矩阵T61，T61的第四列即为16O O，由于坐标系1相对于坐标系0有绕Z 轴的转动，故需要对其进行转换，转换方法为；116O O ⋅ R ，01R为T10中旋转部分注：Matlab 中向量叉积方法：e=cross (a,b)>> T61=T21*T32*T43*T54*T65 %计算出16O O在坐标系1中的描述>> P161=[s2*d3;d2;c2*d3]>> Rot10=[c1 -s1 0;s1 c1 0;0 0 1] %由T10知道旋转部分变换3*3矩阵>> P160= Rot10* P161 % 与P60最后一列比较 >> z1=[0;0;1] >> e=cross(z1,P160)%可得到Jv 第一列：e =[ -s1*s2*d3-c1*d2; c1*s2*d3-s1*d2;0] （2）.计算2026⨯zp2z 为连杆2坐标系的z 轴单位向量在基坐标系0中的描述；206p为连杆2坐标系原点到连杆6坐标系原点连线矢量26O O，在基坐标系0中的描述，计算过程为：计算矩阵P62，P62的第四列即为26O O，由于坐标系2相对于坐标系0有姿态变化，故需要对其进行转换，转换方法为；226O O ⋅R ，02R为T20中旋转部分注：Matlab 中向量叉积方法：e=cross (a,b)>> T62= T32*T43*T54*T65 %计算出26O O在坐标系2中的描述>> P262=[0;-d3;0]>> Rot20=[c1*c2 -c1*s2 -s1;s1*c2 -s1*s2 c1;-s2 -c2 0] %由T20知旋转部分变换3*3矩阵 >> P260= Rot20* P262 >> z2=[-s1;c1;0] >> e=cross(z2, P260)%可得到Jv 第一列：e =[c1*c2*d3; s1*c2*d3; -s1^2*s2*d3-c1^2*s2*d3]（3）.由于连杆3坐标系为移动坐标系，故起对连杆6的速度贡献不能计算为3036⨯zp ，而应该为Z3的单位向量在基坐标系0中的表示；故由T30直接可得Jv 第三列为：1212320⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦c s s s z c（4）.由于坐标系4、5、6和坐标系6的坐标原点重合故对应6066)=⨯=⨯ i i ()q (q i i O i i i v z O O z p 的计算结果均为0 ，于是可得3561241234561212312312121231231223211241412414124514512511241412414124500000000000000⎡⎤=⎢⎥⎢⎥⎣⎦---+-=------+-+-++v v v v v v J J J J J J J J J J J J J c d s s d c c d c s s d c s d s c d s s s d c s c c s s c c c s s c c c c s s s s c s c c s c s c c s c s c c s c c s c ωωωωωω14512524242455210⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥-+⎢⎥⎣⎦s s s s c s s s s s c s c c 五.试验体会：掌握相关软件，认真分析实验要求，克服试验中的困难，争取做出符合要求的结果。