4)机器人静力学和雅克比实验

实验（4）机器人机器人静力学和雅克比实验一、实验目的：1）理解机器人角速度的相关概念；2）对构建的机器人进行速度分析；3）了解和熟悉机器人雅克比矩阵的含义，4）能够使用simulink构建机器人仿真模型。

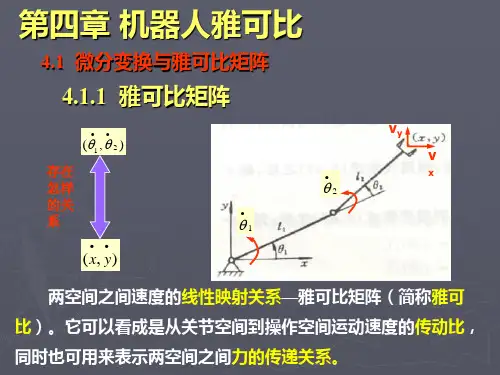
二、雅克比矩阵图1 机器人雅克比矩阵在机器人学中，通常使用雅克比将关节速度与操作臂末端的笛卡尔速度联系起来：在matlab工具箱中，求取机器人雅克比矩阵函数为，J = (qr) ，其中p560为机器人名。

逆雅克比矩阵：分析雅克比矩阵：其中，在matlab工具相中对应函数为，推导可得，变换为，简化模型化为，在matlab工具箱中，对应的RPY的雅克比速度映射函数，该函数为从 RPY角速度到角速度的雅克比变换函数。

即上式中的。

在matlab工具箱中，对应的ZYZ欧拉角的雅克比速度映射函数，>> eul2jac,,ans =对应书中p113页中公式（5-41和5-42）。

综上可得到解析型雅克比，三、基于simulink的机器人仿真模型建立，要求机器人末端以一定1）新建simulink 模型文件，保存为testrobotJ ； 2）在命令窗口中键入roblocks ，调出机器人library 库； 3）打开simulink 库；4）在新建的simulink 模型文件中，从机器人库和simulink 库中查找相应的函数模型按给定例子搭建；simulink/Discrete roblocks/Kinematicssimulink/User-Defined Functions matlab functionsimulink/Math OperationsReshapesimulink/Sourcesroblocks/Robot GraphicsDSP System Toolbox/Math functions/ matrices and Linear Algebra/matrix Operationssimulink/Discrete Discrete Time Integrator图机器人库图关节伺服单元（joint servo）和常量所在库图输出（out）和matlab自定义函数库（matlab function）图矩阵多通道库各模块的参数设置如下图：5）命令窗口中运行mdl_puma560；6）运行建立的模型testrobotJ；7）查看仿真结果。

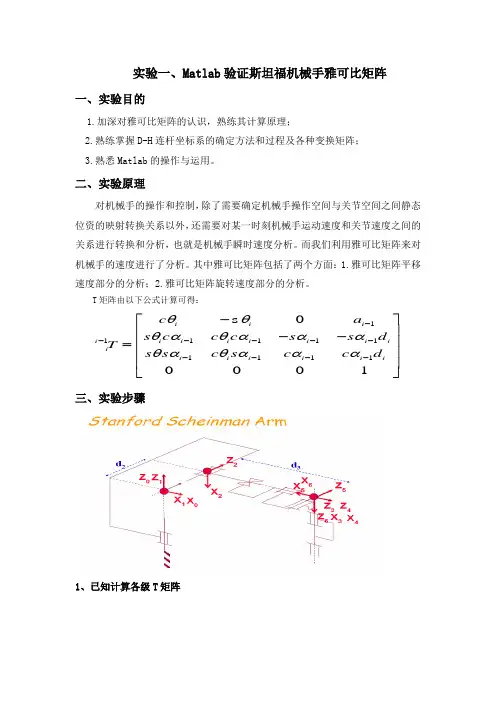
实验一、Matlab 验证斯坦福机械手雅可比矩阵 一、实验目的1.加深对雅可比矩阵的认识，熟练其计算原理；2.熟练掌握D-H 连杆坐标系的确定方法和过程及各种变换矩阵；3.熟悉Matlab 的操作与运用。

二、实验原理对机械手的操作和控制，除了需要确定机械手操作空间与关节空间之间静态位资的映射转换关系以外，还需要对某一时刻机械手运动速度和关节速度之间的关系进行转换和分析，也就是机械手瞬时速度分析。

而我们利用雅可比矩阵来对机械手的速度进行了分析。

其中雅可比矩阵包括了两个方面：1.雅可比矩阵平移速度部分的分析；2.雅可比矩阵旋转速度部分的分析。

T 矩阵由以下公式计算可得：1111111111s 0001iii i i i i i i i i ii i i i i i c a s c c c s s d T s s c s c c d θθθαθαααθαθααα-----------⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥⎣⎦三、实验步骤1、已知计算各级T 矩阵665544445436546655221132210321220000000010001000000000100001000100011000000000100101000001001---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦--⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥===⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦-c s c s c s s c T T T s c s c c s c s d d T T T s c 1100001001⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦s c 2、计算出各连杆坐标系到基坐标系0的变换矩阵：11110111212112112121121022221211213212121121321203222000000001010010000000100-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦----⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥==⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦---+++=-可知可知c s s c T z c c c s s s d s s c s s c c d c T z s c c c s c s c d s s d s c c s s s d s c d T s c c d 12123320010⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦可知c s s s z c 1241412414121231212414124141212312042424223124141251241451251241412312124145050001()()()----⎡⎤⎢⎥+-++⎢⎥=⎢⎥-⎢⎥⎣⎦--------+-=++c c c s s c c s s c c s c s d s d s c c c s s c s c c s s s s d c d T s c s s c c d c c c s s c s s c c c s s s c s c c c s s c c s d s d s c c c s c s T 12512414512512414123122423124514512512312124514512512312062455223()2452524525000112345600⎡⎤⎢⎥-+--+--+++⎢⎥⎢⎥-⎢⎥⎣⎦-+-++++=-s s s c c c s s s s c s c s c c s s d c d s c c c s s c s c c s s c d X X c c c s s s s c s c c s d s d X X s c c s c s s s s c s s d c d T X X s c s c c c d 01⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦Matlab 计算过程如下：>> clear>> syms c1 s1 c2 s2 c3 s3 c4 s4 c5 s5 c6 s6 d1 d2 d3 d4 d5 d6 a1 a2 a3 a4 a5 a6>> T10=[c1 -s1 0 0;s1 c1 0 0;0 0 1 0;0 0 0 1]>> T21=[c2 -s2 0 0;0 0 1 d2;-s2 -c2 0 0;0 0 0 1] >> T32=[1 0 0 0;0 0 -1 -d3;0 1 0 0;0 0 0 1] >> T43=[c4 -s4 0 0;s4 c4 0 0;0 0 1 0;0 0 0 1] >> T54=[c5 -s5 0 0;0 0 1 0; -s5 -c5 0 0;0 0 0 1] >> T65=[c6 -s6 0 0;0 0 -1 0;s6 c6 0 0;0 0 0 1]>> T20=T10*T21； >> T30=T20*T32； >> T40=T30*T43； >> T50=T40*T54； >> T60=T50*T65；>> T60=simplify(T60)3、用速度矢量合成的方法计算雅可比矩阵Jv 部分：356124123456102040506016263465666124561020162631245600000⎡⎤=⎢⎥⎢⎥⎣⎦⎡⎤⨯⨯⨯⨯⨯=⎢⎥⎣⎦⎡⎤⨯⨯=⎢⎥⎣⎦v v v v v v J J J J J J J J J J J J J z p z p z z p z p z p z z z z z z p z p z z z z z z ωωωωωω 1） 计算1016⨯z p1z 为连杆1坐标系的z 轴单位向量在基坐标系0中的描述；16p 为连杆1坐标系原点到连杆6坐标系原点连线矢量16O O，在基坐标系0中的描述，计算过程为：计算矩阵T61，T61的第四列即为16O O，由于坐标系1相对于坐标系0有绕Z 轴的转动，故需要对其进行转换，转换方法为；0116O O ⋅ R ，01R为T10中旋转部分注：Matlab 中向量叉积方法：e=cross (a,b)>> T61=T21*T32*T43*T54*T65 %计算出16O O在坐标系1中的描述>> P161=[s2*d3;d2;c2*d3]>> Rot10=[c1 -s1 0;s1 c1 0;0 0 1] %由T10知道旋转部分变换3*3矩阵 >> P160= Rot10* P161 % 与P60最后一列比较 >> z1=[0;0;1]>> e=cross(z1,P160) %可得到Jv 第一列： e =[ -s1*s2*d3-c1*d2; c1*s2*d3-s1*d2;0]2） 计算2026⨯z p2z 为连杆2坐标系的z 轴单位向量在基坐标系0中的描述；206p 为连杆2坐标系原点到连杆6坐标系原点连线矢量26O O，在基坐标系0中的描述，计算过程为：计算矩阵P62，P62的第四列即为26O O，由于坐标系2相对于坐标系0有姿态变化，故需要对其进行转换，转换方法为；0226O O ⋅ R ，02R为T20中旋转部分注：Matlab 中向量叉积方法：e=cross (a,b)>> T62= T32*T43*T54*T65 %计算出26O O在坐标系2中的描述>> P262=[0;-d3;0]>> Rot20=[c1*c2 -c1*s2 -s1;s1*c2 -s1*s2 c1;-s2 -c2 0] %由T20知旋转部分变换3*3矩阵>> P260= Rot20* P262 >> z2=[-s1;c1;0]>> e=cross(z2, P260) %可得到Jv 第一列：e =[c1*c2*d3; s1*c2*d3; -s1^2*s2*d3-c1^2*s2*d3]3） 由于连杆3坐标系为移动坐标系，故起对连杆6的速度贡献不能计算为3036⨯z p ，而应该为Z3的单位向量在基坐标系0中的表示；故由T30直接可得Jv 第三列为：1212320⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦c s s s z c4)由于坐标系4、5、6和坐标系6的坐标原点重合故对应6066)=⨯=⨯ i i ()q(q i i O i i i v z O O z p 的计算结果均为0 ，于是可得 35612412345612123123121212312312232112414124141245145125112414124141245000000000000⎡⎤=⎢⎥⎢⎥⎣⎦---+-=------+-+-++v v v v v v J J J J J J J J J J J J J c d s s d c c d c s s d c s d s c d s s s d c s c c s s c c c s s c c c c s s s s c s c c s c s c c s c s c c s c c s c ωωωωωω14512524242455210⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥-+⎢⎥⎣⎦s s s s c s s s s s c s c c 5) 用直接求导的方法验证上面Jv 的计算的正确性：在matlab 中用B=jacobian(f,v)方法直接求导可以获取雅可比矩阵四、实验总结机器人雅可比矩阵能够很好地反映出操作空间与关节空间的速度映射关系，而Matlab 则很好的简化了这种关系求导手段。

雅可比矩阵在机器人静力学中的作用雅可比矩阵在机器人静力学中扮演了关键的角色，它用于描述机器人系统中的运动学和动力学关系。

下面我将逐个回答你的问题，并用易于理解的术语解释。

1. 雅可比矩阵是什么雅可比矩阵是一个将机器人的关节速度与其末端执行器速度之间的关系进行描述的矩阵。

它将机器人关节空间中的速度转化为末端执行器空间中的速度。

雅可比矩阵的每个元素代表了末端执行器速度对于关节速度的敏感程度。

2. 机器人的静力学是什么机器人的静力学研究的是机器人系统在静止或匀速运动时所受到的力学影响。

它关注的是机器人系统在特定关节角度下的受力情况，包括关节力和末端执行器力等。

3. 雅可比矩阵在机器人静力学中的作用是什么雅可比矩阵在机器人静力学中的作用是用于分析机器人系统中的力学平衡和力的传递。

通过雅可比矩阵，我们可以将末端执行器的力转化为关节力，并且可以控制机器人系统中的力分配。

4. 如何利用雅可比矩阵进行力的传递分析在机器人静力学中，我们可以利用雅可比矩阵来分析力的传递和分布。

具体而言，我们可以通过雅可比矩阵将末端执行器上的力转化为关节空间中的力。

这样，我们可以对机器人系统进行力分析，包括力矩的计算和力的传递路径的分析等。

5. 为何需要力的传递分析力的传递分析对于机器人的应用非常重要。

它可以帮助我们理解机器人系统中的力分配情况，从而进行力控制和路径规划等。

通过力的传递分析，我们可以确定机器人系统中各个部分所受到的力，以及力的传递路径是否满足设计要求。

总结起来，雅可比矩阵在机器人静力学中的作用是描述机器人系统中的运动学和动力学关系。

它帮助我们分析机器人系统中的力学平衡和力的传递，从而进行力控制和路径规划等。

通过雅可比矩阵的应用，我们可以将末端执行器的力转化为关节力，并且可以确定机器人系统中各个部分所受到的力，从而进行力的传递分析。

这对于机器人的应用非常重要，能够帮助我们优化机器人的设计和控制，提高其性能和安全性。

实验（4）机器人机器人静力学和雅克比实验一、实验目的：1）理解机器人角速度的相关概念；2）对构建的机器人进行速度分析；3）了解和熟悉机器人雅克比矩阵的含义，4）能够使用simulink构建机器人仿真模型。

二、雅克比矩阵图1 机器人雅克比矩阵在机器人学中，通常使用雅克比将关节速度与操作臂末端的笛卡尔速度联系起来：在matlab工具箱中，求取机器人雅克比矩阵函数为，J = p560.jacob0(qr) ，其中p560为机器人名。

逆雅克比矩阵：分析雅克比矩阵：其中，在matlab工具相中对应函数为，推导可得，变换为，简化模型化为，在matlab工具箱中，对应的RPY的雅克比速度映射函数，该函数为从RPY角速度到角速度的雅克比变换函数。

即上式中的。

在matlab工具箱中，对应的ZYZ欧拉角的雅克比速度映射函数，>> eul2jac(0.1,0.2,0.3)ans =0 -0.0998 0.19770 0.9950 0.01981.0000 0 0.9801对应书中p113页中公式（5-41和5-42）。

综上可得到解析型雅克比，三、基于simulink的机器人仿真模型建立，要求机器人末端以一定的速度运行。

simulink/Math Operationssimulink/SourcesDSP System Toolbox/Math simulink/Discrete图 机器人库图关节伺服单元（joint servo）和常量所在库图输出（out）和matlab自定义函数库（matlab function）图矩阵多通道库各模块的参数设置如下图：5）命令窗口中运行mdl_puma560； 6）运行建立的模型testrobotJ ； 7）查看仿真结果。

-0.50.5-0.500.51-1-0.500.51Xzxy 456Puma 560132YZ图仿真结果四、实验容（1）用simulink建立如下图所示的机器人仿真模型，机器人模型为puma560，可以直接使用机器人库提供的puma机器人模型，并进行观测分析，并且描述然后点击上图中subsystem右键，点击mask->Creat Mask…增加如上edit参数：radius和preq。