导线应力弧垂计算
- 格式:doc
- 大小:761.00 KB
- 文档页数:19

导线弧垂计算通俗易懂
导线弧垂是指在一定距离上,导线下垂的高度。
它在电力输电和电缆架设过程中非常重要,因为合理的导线弧垂能够保证导线的安全性和稳定性。
导线弧垂的计算可以通过以下步骤进行:
1. 确定导线的线性密度:导线的线性密度是指单位长度上的导线重量。
可以通过查找或测量导线的规格和质量来确定。
2. 确定支持点的高度差:支持点是指导线安装的起始点和终点。
测量起始点和终点之间的高度差。
3. 计算跨距:跨距是指支持点之间的水平距离。
测量支持点之间的水平距离。
4. 计算导线的自重:导线的自重是指导线自身重量所产生的垂直力。
可以通过导线的线性密度乘以跨距来计算。
5. 计算附加负荷:在考虑其他外力时,如风力和冰覆盖等,导线还需要考虑附加的负荷。
这些负荷可以通过各种标准和规范来确定。
6. 计算总负荷:总负荷是指导线受到的所有力的总和,包括自重和附加负荷。
7. 计算导线弧垂:导线弧垂可以通过将总负荷除以跨距的平方
来计算。
以上是导线弧垂计算的通俗易懂的步骤。
通过这些计算,可以确定导线安装时需要保持的适当弧垂,以确保导线的安全性和稳定性。

导线控制应力判断方法及用微机进行弧垂计算导线在输电线路中起着承载电流和重量的作用。
在输电线路中,导线的弧垂和应力是十分重要的参数,其合理的控制对于线路的安全运行和寿命有着重要影响。
本文将介绍导线控制应力的判断方法,并讨论使用微机进行弧垂计算的原理和步骤。
一、导线控制应力的判断方法导线的应力可以通过以下方法进行判断和控制。
1.等效应力法等效应力法是通过计算导线的总应力来判断导线是否超过了允许的应力值。
总应力包括机械应力、热应力和冲击应力等。
计算公式如下:σ=σm+σt+σi其中,σ为总应力,σm为机械应力,σt为热应力,σi为冲击应力。
2.拉线法拉线法是通过拉线仪等仪器直接测量导线的应力。
通过对导线进行拉线实验,可以得到导线的弹性限度,进而判断导线的应力是否超过了允许的范围。
3.挠度法挠度法是通过测量导线的挠度来判断导线的应力是否超限。
通过测量导线的弧垂和支立点的高度差,可以计算出导线的应力。
以上方法都是基于导线的物理特性和力学原理来进行判断的,可以得到较为准确的结果。
但要注意的是,不同类型的导线在应力判断上可能存在差异,需要根据具体情况选择合适的方法。
二、用微机进行弧垂计算的原理和步骤微机弧垂计算方法是基于物理和数学原理,通过计算机算法进行弧垂计算,从而得到导线的弧垂和应力等参数。
其原理和步骤如下:1.建立导线模型首先需要建立导线的模型,包括导线的几何形状、材料性质和线路条件等。
导线的几何形状包括导线的横截面形状、弹性系数和断裂应变等。
2.计算导线的张力通过导线的拉力计算公式,根据导线的长度、重力和线路条件等参数,计算导线的张力。
导线的张力是导线弧垂计算的基础。
3.计算导线的弧垂根据导线的张力和线路条件,使用弧垂计算公式,通过迭代计算,得到导线的弧垂。
常用的弧垂计算方法有杨氏公式、西格尔公式和拉平公式等。
4.判断导线应力是否超限通过计算得到导线的应力,使用上述的导线控制应力的判断方法,判断导线的应力是否超过了允许的范围。


第二章 导线张力(应力)弧垂计算第一节 导线和地线的机械物理特性与单位荷载一、导线的机械物理特性导线的机械物理特性,一般指破坏张力、弹性系数、热膨胀系数。
(一) 导线的破坏张力对导线作拉伸试验,将测得瞬时拉断力。
利用多次测量结果,可以建立一组经验公式来计算导线的瞬时拉断力。
考虑到施工和运行中导线接头、修补等因素,设计用导线破坏张力取其实测或计算瞬时拉断力T p 的95%,即 T ps =0.95T p (2-1-1) 式中 T p —导线的瞬时拉断力,N ;T ps —导线的破坏张力,N 。
(二)导线的弹性系数物体的弹性系数也称为弹性模量。
导线的弹性系数是指在弹性限度内,导线受拉力作用时,其应力与相对变形的比例系数,通过试验得出的应力-应变曲线确定,可表示为Tl T E A l A σεε===∆ (2-1-2)式中 T —导线拉力,N ;l 、Δl —导线的原长和伸长,m ;σ—导线的应力,即单位截面的张力,σ=T/A ,N/mm ²; ε—导线的相对变形,ε=Δl/l ; A —导线的截面积,mm ²; E —导线的弹性系数,N/mm ²。
钢芯铝绞线的弹性系数按下式近似计算1s Al E mE E m+=+ (2-1-3)式中 E Al 、E s 、E —分别为铝、钢和综合弹性系数,N/mm ²,E s =190000 N/mm ², E Al =55000 N/mm ²;m =A Al /A s —铝对钢的截面比m =A Al /A s 。
(三)导线的热膨胀系数导线温度升高1℃所引起的相对变形,称为导线的热膨胀系数,可表示为 /t αε=∆ (2-1-4) 式中 ε—温度变化引起的导线相对变形,ε=Δl/l ;Δt —温度变化量,℃;α—导线的热膨胀系数,1/℃。
钢芯铝绞线的热膨胀系数的计算式为s s Al Al s Al E m E E mE ααα+=+ (2-1-5)式中 αAl 、αs 、α—分别为铝、钢和综合热膨胀系数,1/℃。
![[架线]导地线各种弧垂的含义及计算方法(附计算表格),彻底弄懂弧垂](https://uimg.taocdn.com/d68a65cb185f312b3169a45177232f60ddcce7e5.webp)
[架线]导地线各种弧垂的含义及计算方法(附计算表格),彻底弄懂弧垂01-导地线各种弧垂的含义弧垂,又叫弛度,行业外叫“挠度”。
一般定义为:导线悬挂曲线上任意一点到两侧悬挂点连线之间的垂直距离(即任意点弧垂)。
在工程设计、施工、运行中,涉及到观测弧垂、竣工弧垂、平视弧垂(分小平视弧垂和大平视弧垂)、任意点弧垂、最大弧垂、中点弧垂和百米弧垂等诸多术语。
我们施工平时常用的弧垂,有观测弧垂、竣工弧垂、百米弧垂。
为方便初学者使用,将各种弧垂的含义逐一解释如下。
1)观测弧垂,就是某一温度下,现场观测时需要达到的弧垂。
高差不大的情况下,观测弧垂=竣工弧垂,只有连续倾斜地形工况下,才需要区分观测弧垂和竣工弧垂。
施工时,需要根据设计图纸要求,先计算竣工弧垂,然后根据计算出来的竣工弧垂,进一步计算出观测弧垂和线夹安装位置调整值(俗称“爬山值”)。
当导地线弧垂稳定达到观测弧垂时,停止紧线,开始进行附件安装,直线塔附件安装时,需要对线夹安装位置进行调整,也就是说线夹安装的位置不一定是导线与滑车的中心,正常线夹安装完毕,悬垂串应呈竖直状态,各档的弧垂由观测弧垂值变成竣工弧垂值。
观测弧垂、紧线弧垂、施工弧垂,基本上都是同一个意思。
孤立档的观测弧垂,在以前,孤立档或构架档紧线,是一端挂好耐张瓷瓶串,然后在另一端不带瓷瓶串紧线,弧垂紧到设计所规定的紧线弧垂时,再将耐张瓷瓶串挂到导线上,由于瓷瓶串自重比载往往比导线重很多,弧垂会发生变化。
紧线完毕挂耐张串前的弧垂,称之为观测弧垂、紧线弧垂或施工弧垂,两侧瓷瓶串均安装完毕后的弧垂,叫竣工弧垂。
如今的紧线施工工艺,是两端均带瓷瓶串紧线,其中一端事先压接完毕,另一端通过卡线器、钢丝绳短套临时与瓷瓶串金具连接,紧线完毕画印、断线压接,然后过牵引挂到金具上,弧垂直接定型,直接达到竣工弧垂。
2)竣工弧垂,附件安装完毕之后的弧垂值,是与观测弧垂、紧线弧垂、施工弧垂相对而言的。
通过上面观测弧垂的阐述,相信大家已经有了初步的理解。

输电线路当前温度的弧垂怎么换算到最高温度的弧垂
先收集到该线路的相关资料,查出导线型号,查出导线比载或者计算出导线比载,导线的比载计算方法是:
公式中的q为导线单位长度的重量(kg/km),g为重力加速度,一般取
g=9.80665m/s2, A为导线的截面积(mm2).
然后测量的当前的弧垂及该档的档距,计算出观察时的应力:
l为该档的档距,单位m; r为第一步中的比载,f观测为我们观察时的弧垂,σ观测为我们观察时求出的观测档所在耐张段的代表档距的代表应力。
然后通过状态方程式求出最高温时的应力。
公式中的E为导线弹性系数,a为温度膨胀系数,根据导线型号查出,r与l 就是上述公式的比载与档距,t高温与t观察分别为高温的温度与测量弧垂时的温度,通过此公式计算出,高温应力。
知道高温应力,知道比载与档距,就可以通过弧垂公式求出弧垂,计算公式如下:
另外也可以根据该工程的资料,直接查出高温时的该档距所在耐张段的代表应力,比载与该档距,就可以直接求出弧垂,不用观测。

架空线的弧垂、线长及应力计算1 弧垂、线长计算架空线由于档距很大,材料的刚性影响可忽略不计,架空线的形状就像一条两端悬挂的柔软的索链。
所以,可以按悬链线进行计算其弧垂和线成,其方程为:弧垂 f = σ/g〔ch(gl/2σ)-1〕线长L = 2σ/g〔sh(gl/2σ)〕上二式写成级数形式展开后为:f = σ/g{〔1+(L12g2/8σ2)+(L14g4/38σ4)+……〕-1}= (L12g/8σ)+(L14g3/38σ3)+……L = 2σ/g{(L1g/2σ)+(L13g3/48σ3)+(L15g5/3840σ5)+……}= L1+(L13g2/24σ2)+(L15g4/1920σ4)+……为了简化计算,工程上取f第一项计算弧垂,取L前二项计算线长(即用抛物线方程代替悬链线方程近似计算):f = L12g/8σL = L1+(L13g2/24σ2)= L1+(8 f2/3 L1)式中,L1—档距,m;g —架空线的比载,N/m·mm2g = W/S其中,W —单位长度导线重量,N/m;S —导线截面积,mm2σ—架空线最低点应力(水平应力),N/mm2。
按上式计算的误差:当弧垂不大于档距的5%时,线长误差率小于15×10-4%。
几种情况弧垂计算:①在交叉跨越档距中一般需计算被跨越物上面任一点导线的弧垂f x,以便校验交叉跨越距离。
档距中任一点导线的弧垂按下式计算:f x = x(L1-x)g/2σ= 4 f x(1-x/L1)/L1式中,x—从悬挂点至计算坐标点的水平距离,m。
②在悬挂点具有高差的档距中架空线的计算需用斜抛物线法,即:L =(L1/cosφ)+(L13g2 cosφ/24σ2)f = L12g/8σcosφf x = x(L1-x)g/2σcosφ式中,φ—高差角,φ = arc tg(h/L1)其中,h —高差;L1—档距。
2 应力计算①架空线任一点处的应力架空线各点所受应力的方向是沿架空线切线方向变化的,最低点处的应力称为水平应力,只要知道最低点应力,架空线上任一点的应力都可以用下式计算求得:σX= σ+(f-f x)g式中,σX—架空线任一点处的应力,N/mm2;σ—架空线最低点应力(水平应力),N/mm2;f —架空线弧垂,m;f x—计算点导线的弧垂,m;g —架空线比载,N/m·mm2。

软导线拉力、弧垂、应力计算书工程:算例依据:(1)电力工程设计手册(变电站设计);(2)电力工程设计手册(架空输电线路设计);(3)DL/T 5457 变电站建筑结构设计规程软件:变电电气计算计算时间:2023年6月26日1. 输入条件(1)构架编号:G1;跨距32.50m;高差1.25m;允许弧垂1.00m;引下线2 条,间距L1=9m、L2=11.5m、L3=12m(距左侧构架);电压等级:110 kV;气象条件:气象区7(最大风速30m/s;覆冰10mm;覆冰风速10m/s;安装检修风速10m/s;最低温度-40℃;最大风速时温度-5℃;安装检修时温度-15℃)。
(2)导线:2×LGJ-400/35;最高工作温度70℃;间隔棒安装间距2m;间隔棒重1.2kg。
(3)左侧(A串)跳线:2×LGJ-400/35;长度3.5m;线夹重11.2kg;间隔棒重1.2kg;间隔棒安装间距2m。
(4)右侧(B串)跳线:无;线夹重11.2kg。
(5)左侧绝缘子串(A串):单串;单片绝缘子重5.8kg;绝缘子片数9片;组装金具重2.4kg;串长1.574m。
(6)右侧绝缘子串(B串):单串;单片绝缘子重5.8kg;绝缘子片数9片;组装金具重6.4kg;串长1.834m。
(7)引下线1:2×LGJ-400/35;长度7.8m;线夹重9.6kg;间隔棒重1.2kg;间隔棒安装间距2m。
(8)引下线2:2×LGJ-400/35;长度6.9m;线夹重9.6kg;间隔棒重1.2kg;间隔棒安装间距2m。
2. 导线安装曲线及拉力、弧垂表2.1导线安装曲线2.2导线安装拉力、弧垂表3. 构架提资(构架编号:G1)4. 出线构架(如有),其外侧导地线最大拉力导线:5 kN;地线:3 kN。

导线的通用应力弧垂曲线图安岳供电公司 李荣久编制一、通用应力弧垂曲线图绘制方法只要导线的弹性系数E 、热膨胀系数α、自重比载g 1相同,就可以用同一幅应力弧垂通用曲线图。
城镇架空配电线路的档距一般不超过50m ,通常都不设计拉线而以能承受较大张力的杆塔作为转角和终端杆塔。
导线的最大设计应力一般不是由其基本安全系数而是由杆塔能承受的许用张力控制,因此每一种导线的最大设计应力都不是固定的。
在这种情况下,用应力弧垂通用曲线就有突出的优点。
1. 应力曲线。
计算公式为221()24g E nl y σσ=- ,以y 为纵坐标,nl 为横坐标,并给σ以选定值和以nl 为自变数,便可绘制出很多nl 与y 的关系曲线,即应力曲线群。
2. 弧垂曲线。
计算公式为 2212()8()83()g nl E nf y nf nl =-,同样,给定nf 以各种值,便可绘制出nl 与y 的关系曲线,即弧垂曲线群。
3. 温差尺。
温差尺的计算式为 ()x b y E t t E t αα=-=∆,以Δt 等于5或10的倍数值代入式中求得y 值,以此y 值为坐标画横线,即得温差尺线群。
式中 E —导线的弹性系数,N/mm 2;α—导线的热膨胀系数,1/℃;g 1—导线的自重比载, N/ m. mm 2;σb 、σx —分别为控制气象条件和待求气象条件的导线应力,N/mm 2,g b 、g x — 分别为控制气象条件和待求气象条件的比载,N/ m. mm 2,n —比载比率,n = g/ g 1,g 根据计算气象条件选用g 6或g 7,n b = g b / g 1, n x = g x / g 1;t b 、 t x —分别为控制气象条件和待求气象条件的气温,℃;l —导线的代表档距,m 。
二、使用方法1. 确定控制条件。
在有覆冰地区,最低气温、覆冰和最大风速气象条件都可能为控制条件,在最大使用应力确定后,可以用前面计算临界档距的方法确定控制条件及其控制范围,也可以在图中直接查找某一代表档距的控制条件。

架空线路弧垂、应力及线长计算1、导线的机械特性和荷载 1.1导线的机械特性导线的特性参数是指导线的瞬时破坏应力σp 、弹性系数E 、温度线膨胀系数α以及密度γ等数据。
这些特性参数是对导线进行机械计算的重要依据,一般可从有关资料或手册中得到。
1.1.1导线的瞬时破坏应力σp 。
对导线做拉伸试验时,将测得的瞬时拉断力除以导线的截面积,即得导线的瞬时破坏应力σp ,计算公式为σp =AT p (N/mm 2) (ZY0400201002-1)式中:T p —导线的瞬时拉断力,N ;A —导线的截面积,mm 2。
对于钢芯铝绞线来说,指的是的综合瞬时破坏应力σp ,可以通过下面的经验公式求得σp =sa sps s ap a a A A σA σA η++η(N/mm 2) (ZY0400201002-2)式中:ηa —铝线绞合引起的强度损失系数,37股以下绞线ηa =0.95,37股以上绞线ηa =0.9; ηs —钢绞线绞合引起的强度损失系数,取ηa =0.85; σap —铝单线的抗拉强度,N /mm 2; σsp —钢线的抗拉强度,N /mm 2; A a —铝部的截面积; A s —钢部的截面积。
1.1.2导线弹性系数E 。
是指在弹性限度内,导线受拉力作用时,其应力σ与应变ε的比例系数E 。
钢芯铝绞线的弹性系数是一个综合弹性系数E ,可按下式计算aaE E E ++=1a s (N/mm 2) (ZY0400201002-3)式中:E s —单股钢线的弹性系数,N /mm 2; E a —单股铝线的弹性系数,N /mm 2;a —导线铝和钢的截面比,LGJ 型a =5.3~6.0,LGJQ 型a =8.0,LGJJ 型a =4.3~4.4。
1.1.3导线温度线膨胀系数α。
是指导线温度升高1℃时长度伸长的相对值,用公式表示为α=tΔε(1/℃) (ZY0400201002-4)式中:ε—温度变化引起的导线相对变形量;∆t —温度变化量,℃。
输电线路弧垂计算公式好的,以下是为您生成的关于“输电线路弧垂计算公式”的文章:在我们的日常生活中,电的存在就像空气一样不可或缺。
当我们轻轻按下开关,灯光瞬间亮起,电器开始运转,这一切的背后都离不开输电线路的默默工作。
而在输电线路的众多知识中,弧垂计算公式可是一个相当重要的部分。
先来说说啥是输电线路的弧垂。
想象一下,输电线路就像是一条长长的琴弦,被架设在电线杆或者铁塔之间。
由于线路自身的重量,它会在中间部分向下弯曲,形成一个类似于弧形的形状,这个弧形的垂直距离就是弧垂。
那为啥要关注弧垂呢?这可太重要啦!如果弧垂过大,线路可能会离地面太近,容易引发安全事故;要是弧垂过小,线路又会承受过大的张力,影响线路的使用寿命。
所以,准确计算弧垂对于保证输电线路的安全稳定运行至关重要。
接下来,咱们就聊聊输电线路弧垂的计算公式。
常见的计算公式有平抛物线法和悬链线法。
平抛物线法的公式相对简单,它假设输电线路的形状是一个平抛物线。
公式是:f = (g * L^2) / (8 * σ) 。
这里的 f 就是弧垂,g 是导线的比载,L 是档距,σ 是导线的水平应力。
举个例子来说吧,有一次我跟着电力工程师们去现场检修输电线路。
那天阳光特别好,我们来到了一片空旷的田野里,远处的输电线路在蓝天白云的映衬下格外醒目。
工程师们拿着仪器,仔细地测量着档距和导线的各种参数。
其中一个年轻的工程师,一边记录数据,一边嘴里念叨着弧垂的计算公式。
他的神情专注而认真,额头上还冒出了细密的汗珠。
我在旁边看着,心里不禁感叹,这看似简单的公式背后,可是他们日复一日的辛勤付出和对工作的严谨态度。
悬链线法的公式相对复杂一些,但它更接近实际情况。
不过在实际工程中,平抛物线法已经能够满足大多数的精度要求。
在实际应用这些公式的时候,还需要考虑很多因素,比如温度、风速、覆冰情况等等。
因为这些因素都会影响导线的张力和弧垂的大小。
总之,输电线路弧垂的计算可不是一件简单的事情,它需要我们综合考虑各种因素,选择合适的计算公式,并且要保证测量数据的准确性。
浅谈输电线路弧垂的简易计算摘要:本文主要针对输电线路弧垂的计算进行分析,明确了输电线路弧垂计算的基本理念,以及基本的理论要求,进而简单论述了输电线路弧垂的计算方法和计算的过程,供参考和借鉴。
关键词:输电线路;弧垂;简易计算前言针对输电线路弧垂的计算问题,我们要进一步总结和分析,探讨其计算的要求和要点,才能够为今后进一步研究输电线路弧垂的相关问题奠定基础,提高研究水平。
1基于弧垂的输电线舞动输电线舞动是覆冰输电线在风的激励下产生的一种低频、大振幅自激振动。
输电线的舞动已经对我国很多地区的输电线路造成了很大的危害。
因此我们需要及时有效的对输电线舞动进行实时监控。
随着视频分析及图像处理技术的快速发展,在输电线路上定位摄像机或者进行航拍取样,对输电线进行实时的视频监控,成为一种较为可行的输电线舞动监测方法。
在视频分析中,应用数字图像处理技术对采集到数据进行分析计算,可以为防治输电线的舞动提供大量准确的数据支持。
相关工作在国内外已经有了开展。
自20世纪30年代起,国外学者开始对导线舞动进行了大量的试验和理论研究!介绍了我国近年来在输电线防舞动方面的研究成果,以及由此开发的专利产品双摆防舞器和整体式偏心重锤的应用情况。
给出了输电线舞动的有限元分析方法,在此基础上编写了计算导线舞动的有限元程序,计算实例模拟了舞动的全过程,探讨了风速、攻角等对舞动的影响。
在现代图像分析与计算机视觉技术日益完善的情况下,针对一些特定的舞动形态,图像检测手段将是一种很好的选择。
采用图像分析与视觉计算方法,实现了对输电线路横向舞动的角度计算。
首先采用固定于杆塔上的摄像头拍摄电缆图像,根据指定区域及预设数量检测出电缆,并进行曲线拟合得到相关参数,再采用简化的横向舞动模型,推算舞动角度与图像中电缆轨迹参数的关系,最后计算出输电线路的横向舞动角度,为舞动的动态监测与数据记录提供了一种新的思路。
架空线在输电线路中是一种被经常采用的形式。
一般来讲,温差过大的地区一般弧垂都会非常小,进而导线就非常容易出现热胀冷缩的现象,这种自然现象就会使导线也发生了一系列的变化。
导线应力弧垂计算导线的应力弧垂计算是为了确定导线的形态以及对导线进行张力设计的重要步骤。
应力弧垂的计算能够保证导线在各种外力的作用下仍能满足导线张力、弧垂和安全等要求。
在导线应力弧垂计算中,需要考虑导线的自重、气候条件(如风速、温度等)以及拉力等因素。
下面将详细介绍导线应力弧垂计算的主要内容。
1.导线自重的计算:导线自重是导线弧垂计算的基础,需要根据导线的材料、截面形状等参数来计算。
常用的导线材料有铝、钢、镀铝钢等,不同材料的密度和弹性模量不同,对导线自重的计算产生影响。
2.外力的计算:外力包括风力、温度应力等。
风力是导线设计中最重要的外力之一,通过风压力和风速来进行计算。
可以使用一些风压公式和根据当地的气象数据来计算风力对导线的作用力。
温度应力是由于导线在高温和低温环境下的膨胀和收缩所引起的。
根据导线的线膨胀系数和温度变化范围,可以计算出温度应力对导线张力和弧垂的影响。
3.导线张力的计算:导线张力是导线应力弧垂计算中即需要考虑的因素。
导线张力通过外力和导线自重的作用来计算。
在计算过程中,需要使用悬链线理论、拉力平衡方程等公式来进行计算。
4.弧垂的计算:导线在张力作用下会形成一定的弧垂,弧垂的大小与导线自重、张力、气象因素等有关。
通过计算张力和弧垂之间的关系,可以确定导线的最佳弧垂,确保导线的安全性和可靠性。
在导线应力弧垂计算中,还要考虑导线的固定方式和绝缘子的位置、串控因素等因素对导线张力和弧垂的影响。
通过综合考虑这些因素,可以得出合理的导线应力弧垂计算结果,从而指导导线的设计、安装和维护工作。
总之,导线应力弧垂计算是非常重要的工程设计环节,直接关系到导线的安全性和可靠性。
合理的导线应力弧垂计算结果可以保证导线在各种外力的作用下保持良好的形态,从而确保电力系统的正常运行和供电质量的稳定。
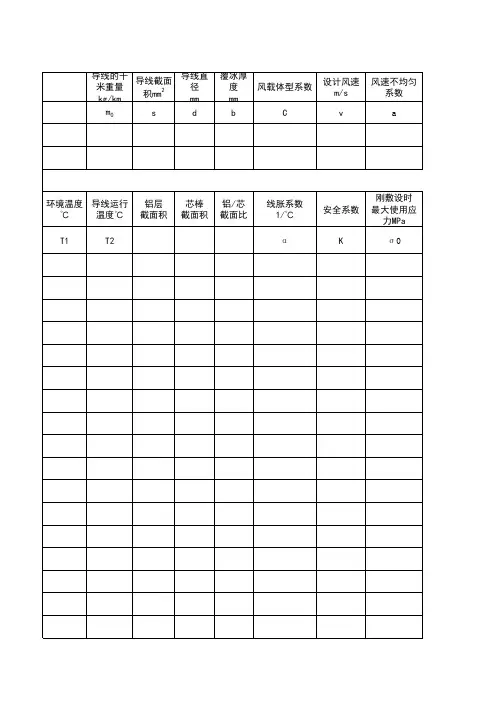
导线应力弧垂计算一、确定相关参数表二 LGJ-300/50型导线参数 二、相关比载计算1. 自重比载)/(1006.341036.34880665.912100,0331m Mpa A qg --⨯=⨯⨯==)(γ2. 冰重比载)/(1060.111036.348)26.245(5728.2710)(728.270,53332m Mpa A b d b ---⨯=⨯+⨯⨯=⨯+=)(γ3.垂直总比载)/(1066.45050,00,53213m Mpa -⨯=+=),()()(γγγ 4.无冰风压比载5.626.1106.122===V W V (Pa)63.3906.1256.122===V W V (Pa)1)外过电压、安装有风: 33241036.3485.6226.241.185.00.110sin 10,0--⨯⨯⨯⨯⨯=⨯=θμαβγA W d v sc f c )( =4.103-10⨯(Mpa/m )2)最大设计风速:计算强度:33241036.34863.39026.241.185.00.110sin 25,0--⨯⨯⨯⨯⨯=⨯=θμαβγA W d v sc f c )(=25.433-10⨯(Mpa/m )低于500kv 的线路c β取1.0,计算强度时f α按表取0.85,当d ≥17mm 时sc μ取1.1. 计算风偏:33241036.34863.39026.241.175.00.110sin 25,0--⨯⨯⨯⨯⨯=⨯=θμαβγA W d v sc f c )( =22.443-10⨯(Mpa/m ) 计算风偏时f α取0.75 3)内过电压:625.1406.1156.122===V W V (Pa) 33241036.348625.14026.241.185.00.110sin 15,0--⨯⨯⨯⨯⨯=⨯=θμαβγA W d v sc f c )( =9.163-10⨯(Mpa/m )5. 覆冰风压比载5.626.1106.122===V W V 32510sin )2(10,5-⨯+=θμαβγAW b d B vsc f c )( 3-1036.3485.621026.241.12.10.10.1⨯⨯+⨯⨯⨯⨯=)()(m Mpa /1011.83-⨯=6. 无冰综合比载外过电压、安装有风:)/(1031.341010.406.3410,00,025,033-2224216m Mpa -⨯=⨯+=+=)()()(γγγ 最大设计风速(计算强度):)/(1051.421043.2506.3425,00,025,033-2224216m Mpa -⨯=⨯+=+=)()()(γγγ 最大设计风速(计算风偏):)/(1079.401044.2206.3425,00,025,033-2224216m Mpa -⨯=⨯+=+=)()()(γγγ 内过电压:)/(1027.351016.906.345.12,00,010,033-2224216m Mpa -⨯=⨯+=+=)()()(γγγ 7. 覆冰综合比载)/(1037.4610,50,510,5325237m Mpa -⨯=+=)()()(γγγ三、确定应力值(1)最大使用应力:)(8.1125.20.282Mpa kp===σσ (2)年平均运行应力上线:)(5.70%250.282%25][Mpa p pj =⨯=⨯=σσ四、计算临界档距,判断控制气象条件因为覆冰与最大风情况下的最大使用应力和气温都相同,又覆冰时的比载大于最大风时的比载,故最大风不再作为控制气象图条件考虑。
表四 比值]/[0σγ计算结果及其排序表公式:])][()][[(]][][[24202000ii j j i j i j ij E t t E l σγσγασσ--+-=)(])10302.0()10411.0[(76000]1054346.18.1128.112[242323--⨯-⨯⨯+-⨯+-⨯=)(ab l =170.72])10302.0()10483.0[(76000]10154346.18.1125.70[242323--⨯-⨯⨯+⨯+-⨯=)(ac l =虚数 ])10411.0()10483.0[(76000]5154346.18.1125.70[242323--⨯-⨯⨯+⨯+-⨯=)(bc l =虚数年均温为控制气象条件。
五、状态方程求应力已知年均温为控制气象条件表六已知条件参数状态方程计算式:)(2424-122012210120222202t t E l E l E ---=ασγσσγσ 1. 最高温:)(2424-122012210120222202t t E l E l E ---=ασγσσγσ带入数据得:)15-40(4364.15.70241006.34760005.70241006.3476000-2223-202223-02⨯-⨯⨯⨯⨯-=⨯⨯⨯l l )()(σσ 即:067.364.3400074.022022302=--+l l σσ)( 当档距为以下各值时,由状态方程求得应力: 50m:05067.364.345000074.022022302=⨯--⨯+σσ)(=02σ38.86(Mpa)100m:010067.364.3410000074.022022302=⨯--⨯+σσ)( =02σ45.20(Mpa)150m:015067.364.3415000074.022022302=⨯--⨯+σσ)( =02σ50.44(Mpa)200m:020067.364.3420000074.022022302=⨯--⨯+σσ)( =02σ54.49(Mpa)250m:025067.364.3425000074.022022302=⨯--⨯+σσ)( =02σ57.58(Mpa)300m:030067.364.3430000074.022022302=⨯--⨯+σσ)( =02σ59.95(Mpa)350m:035067.364.3435000074.022022302=⨯--⨯+σσ)( =02σ61.78(Mpa)400m:040067.364.3440000074.022022302=⨯--⨯+σσ)( =02σ63.21(Mpa)450m:045067.364.3445000074.022022302=⨯--⨯+σσ)( =02σ64.33(Mpa)500m:050067.364.3450000074.022022302=⨯--⨯+σσ)(022. 最低温:)(2424-122012210120222202t t E l E l E ---=ασγσσγσ 带入数据得:)15-10-(4364.15.70241006.34760005.70241006.3476000-2223-202223-02⨯-⨯⨯⨯⨯-=⨯⨯⨯l l )()(σσ 即:067.341.10600074.022022302=--+l l σσ)( 当档距为以下各值时,由状态方程求得应力:50m:05067.341.1065000074.022022302=⨯--⨯+σσ)( =02σ105.39(Mpa)100m:010067.341.10610000074.022022302=⨯--⨯+σσ)( =02σ102.50(Mpa)150m:015067.341.10615000074.022022302=⨯--⨯+σσ)( =02σ98.30(Mpa)200m:020067.341.10620000074.022022302=⨯--⨯+σσ)( =02σ93.58(Mpa)250m:025067.341.10625000074.022022302=⨯--⨯+σσ)( =02σ88.82(Mpa)300m:030067.341.10630000074.022022302=⨯--⨯+σσ)( =02σ85.06(Mpa)350m:035067.341.10635000074.022022302=⨯--⨯+σσ)( =02σ82.23(Mpa)400m:040067.341.10640000074.022022302=⨯--⨯+σσ)(02450m:045067.341.10645000074.022022302=⨯--⨯+σσ)( =02σ78.02(Mpa)500m:050067.341.10650000074.022022302=⨯--⨯+σσ)( =02σ76.75(Mpa) 3.最大风:)(2424-122012210120222202t t E l E l E ---=ασγσσγσ 带入数据得:)15-5-(4364.15.70241006.34760005.70241051.4276000-2223-202223-02⨯-⨯⨯⨯⨯-=⨯⨯⨯l l )()(σσ 即:072.520.9900074.022022302=--+l l σσ)( 当档距为以下各值时,由状态方程求得应力:50m:05072.520.995000074.022022302=⨯--⨯+σσ)( =02σ98.81(Mpa)100m:010072.520.9910000074.022022302=⨯--⨯+σσ)( =02σ97.78(Mpa)150m:015072.520.9915000074.022022302=⨯--⨯+σσ)( =02σ96.40(Mpa)200m:020072.520.9920000074.022022302=⨯--⨯+σσ)( =02σ94.97(Mpa)250m:025072.520.9925000074.022022302=⨯--⨯+σσ)( =02σ93.68(Mpa)300m:030072.520.9930000074.022022302=⨯--⨯+σσ)(02350m:035072.520.9935000074.022022302=⨯--⨯+σσ)( =02σ91.83(Mpa)400m:040072.520.9940000074.022022302=⨯--⨯+σσ)( =02σ91.09(Mpa)450m:045072.520.9945000074.022022302=⨯--⨯+σσ)( =02σ90.51(Mpa)500m:050072.520.9950000074.022022302=⨯--⨯+σσ)( =02σ90.15(Mpa) 4.覆冰无风:)(2424-122012210120222202t t E l E l E ---=ασγσσγσ 带入数据得:)15-5-(4364.15.70241006.34760005.70241037.4676000-2223-202223-02⨯-⨯⨯⨯⨯-=⨯⨯⨯l l )()(σσ 即:081.620.9900074.022022302=--+l l σσ)( 当档距为以下各值时,由状态方程求得应力:50m:05081.620.995000074.022022302=⨯--⨯+σσ)( =02σ99.08(Mpa)100m:010081.620.9910000074.022022302=⨯--⨯+σσ)( =02σ98.78(Mpa)150m:015081.620.9915000074.022022302=⨯--⨯+σσ)( =02σ98.38(Mpa)200m:020081.620.9920000074.022022302=⨯--⨯+σσ)(02250m:025081.620.9925000074.022022302=⨯--⨯+σσ)( =02σ97.43(Mpa)300m:030081.620.9930000074.022022302=⨯--⨯+σσ)( =02σ97.32(Mpa)350m:035081.620.9935000074.022022302=⨯--⨯+σσ)( =02σ97.02(Mpa)400m:040081.620.9940000074.022022302=⨯--⨯+σσ)( =02σ96.88(Mpa)450m:045081.620.9945000074.022022302=⨯--⨯+σσ)( =02σ96.73(Mpa)500m:050081.620.9950000074.022022302=⨯--⨯+σσ)( =02σ96.61(Mpa)5. 安装)(2424-122012210120222202t t E l E l E ---=ασγσσγσ 带入数据得:)15-5-(4364.15.70241006.34760005.70241031.3476000-2223-202223-02⨯-⨯⨯⨯⨯-=⨯⨯⨯l l )()(σσ 即:073.320.9900074.022022302=--+l l σσ)( 当档距为以下各值时,由状态方程求得应力:50m:05073.320.995000074.022022302=⨯--⨯+σσ)( =02σ98.31(Mpa)100m:010073.320.9910000074.022022302=⨯--⨯+σσ)(=02σ95.86(Mpa)150m:015073.320.9915000074.022022302=⨯--⨯+σσ)( =02σ92.38(Mpa)200m:020073.320.9920000074.022022302=⨯--⨯+σσ)( =02σ88.60(Mpa)250m:025073.320.9925000074.022022302=⨯--⨯+σσ)( =02σ85.12(Mpa)300m:030073.320.9930000074.022022302=⨯--⨯+σσ)( =02σ82.24(Mpa)350m:035073.320.9935000074.022022302=⨯--⨯+σσ)( =02σ79.98(Mpa)400m:040073.320.9940000074.022022302=⨯--⨯+σσ)( =02σ78.26(Mpa)450m:045073.320.9945000074.022022302=⨯--⨯+σσ)( =02σ76.94(Mpa)500m:050073.320.9950000074.022022302=⨯--⨯+σσ)( =02σ75.93(Mpa)6. 外过有风)(2424-122012210120222202t t E l E l E ---=ασγσσγσ 带入数据得:)15-15(4364.15.70241006.34760005.70241051.4276000-2223-202223-02⨯-⨯⨯⨯⨯-=⨯⨯⨯l l )()(σσ即:072.55.7000074.022022302=--+l l σσ)( 当档距为以下各值时,由状态方程求得应力:50m:05072.55.705000074.022022302=⨯--⨯+σσ)( =02σ71.45(Mpa)100m:010072.55.7010000074.022022302=⨯--⨯+σσ)( =02σ73.78(Mpa)150m:015072.55.7015000074.022022302=⨯--⨯+σσ)( =02σ76.08(Mpa)200m:020072.55.7020000074.022022302=⨯--⨯+σσ)( =02σ78.16(Mpa)250m:025072.55.7025000074.022022302=⨯--⨯+σσ)( =02σ80.05(Mpa)300m:030072.55.7030000074.022022302=⨯--⨯+σσ)( =02σ81.23(Mpa)350m:035072.55.7035000074.022022302=⨯--⨯+σσ)( =02σ82.59(Mpa)400m:040072.55.7040000074.022022302=⨯--⨯+σσ)( =02σ83.46(Mpa)450m:045072.55.7045000074.022022302=⨯--⨯+σσ)( =02σ84.17(Mpa)500m:050072.55.7050000074.022022302=⨯--⨯+σσ)( =02σ84.72(Mpa)7. 外过无风)(2424-122012210120222202t t E l E l E ---=ασγσσγσ 带入数据得:)15-15(4364.15.70241006.34760005.70241006.3476000-2223-202223-02⨯-⨯⨯⨯⨯-=⨯⨯⨯l l )()(σσ 即:5.7002=σ(Mpa)8. 操作过电压)(2424-122012210120222202t t E l E l E ---=ασγσσγσ 带入数据得:)15-15(4364.15.70241006.34760005.70241065.3476000-2223-202223-02⨯-⨯⨯⨯⨯-=⨯⨯⨯l l )()(σσ 即:080.35.7000074.022022302=--+l l σσ)( 当档距为以下各值时,由状态方程求得应力:50m:05080.35.705000074.022022302=⨯--⨯+σσ)( =02σ70.56(Mpa)100m:010080.35.7010000074.022022302=⨯--⨯+σσ)( =02σ70.71(Mpa)150m:015080.35.7015000074.022022302=⨯--⨯+σσ)( =02σ70.87(Mpa)200m:020080.35.7020000074.022022302=⨯--⨯+σσ)( =02σ71.03(Mpa)250m:025080.35.7025000074.022022302=⨯--⨯+σσ)(=02σ71.56(Mpa)300m:030080.35.7030000074.022022302=⨯--⨯+σσ)( =02σ71.26(Mpa)350m:035080.35.7035000074.022022302=⨯--⨯+σσ)( =02σ71.33(Mpa)400m:040080.35.7040000074.022022302=⨯--⨯+σσ)( =02σ71.39(Mpa)450m:045080.35.7045000074.022022302=⨯--⨯+σσ)( =02σ71.44(Mpa)500m:050080.35.7050000074.022022302=⨯--⨯+σσ)( =02σ71.47(Mpa)续表六、计算弧垂弧垂计算公式:bl f 028σγ=1.最高温:50m:=⨯⨯⨯=86.388501006.3423-f 0.274(m)100m:=⨯⨯⨯=20.4581001006.3423-f 0.912(m)150m:=⨯⨯⨯=44.5081501006.3423-f 1.90(m)200m:=⨯⨯⨯=49.5482001006.3423-f 3.13(m)250m:=⨯⨯⨯=58.5782501006.3423-f 4.62(m)300m:=⨯⨯⨯=95.5983001006.3423-f 6.39(m)350m:=⨯⨯⨯=78.6183501006.3423-f 8.44(m)400m:=⨯=21.638f 10.78(m)450m:=⨯⨯⨯=33.6484501006.3423-f 13.40(m)500m:=⨯⨯⨯=24.6585001006.3423-f 16.31(m) 2.外过无风:50m:=⨯⨯⨯=5.708501006.3423-f 0.14(m)100m:=⨯⨯⨯=5.7081001006.3423-f 0.55(m)150m:=⨯⨯⨯=5.7081501006.3423-f 1.24(m) 200m:=⨯⨯⨯=5.7082001006.3423-f 2.20(m)250m:=⨯⨯⨯=5.7082501006.3423-f 3.44(m)300m:=⨯⨯⨯=5.7083001006.3423-f 4.96(m)350m:=⨯⨯⨯=5.7083501006.3423-f 6.75(m)400m:=⨯⨯⨯=5.7084001006.3423-f 8.82(m)450m:=⨯=5.708f 11.16(m)500m:=⨯⨯⨯=5.7085001006.3423-f 13.78(m) 3.覆冰无风:50m:=⨯⨯⨯=08.998501006.3423-f 0.11(m)100m:=⨯⨯⨯=78.9881001006.3423-f 0.43(m)150m:=⨯⨯⨯=38.9881501006.3423-f 0.97(m)200m:=⨯⨯⨯=98.9782001006.3423-f 1.74(m)250m:=⨯⨯⨯=43.9782501006.3423-f 2.73(m)300m:=⨯⨯⨯=32.9783001006.3423-f 3.94(m)350m:=⨯⨯⨯=02.9783501006.3423-f 5.78(m)400m:=⨯⨯⨯=88.9684001006.3423-f 7.03(m)450m:=⨯⨯⨯=73.9684501006.3423-f 8.91(m)500m:=⨯=61.968f 11.02(m) 表八 LGJ-300/50型导线弧垂计算表档距(m )最高温(m) 外过无风(m )覆冰无风(m)50 0.27 0.14 0.11 100 0.91 0.55 0.43 150 1.90 1.24 0.97 200 3.13 2.20 1.74 250 4.62 3.44 2.73 300 6.39 4.96 3.94 350 8.44 6.75 5.78 400 10.78 8.82 7.03 450 13.40 11.16 8.91 50016.3113.7811.02七、应力弧垂曲线绘制。