下载文档原格式
《输电线路基础》第章-导线应力弧垂分析-第节-导线的状态讲解课件 (二)
1. 导线应力
- 导线在使用过程中会受到拉力的作用，这种拉力会导致导线产生应力。
- 导线应力的大小与导线的材料、直径、长度以及受力情况有关。
- 导线应力的大小对导线的使用寿命和安全性都有着重要的影响。
2. 弧垂分析
- 弧垂是指导线在两个支点之间的下垂程度。
- 弧垂大小与导线的张力、跨距、重量以及环境温度等因素有关。
- 弧垂分析是对导线状态进行评估的重要手段。
3. 导线状态
- 导线状态包括张力状态、弧垂状态、振动状态等。
- 张力状态是指导线受到的拉力大小，它会影响导线的应力和弧垂。
- 弧垂状态是指导线在两个支点之间的下垂程度，它会影响导线的张力和应力。
- 振动状态是指导线在风力等外力作用下的振动情况，它会影响导线的疲劳寿命和安全性。
4. 导线状态的评估
- 导线状态的评估是对导线安全性和使用寿命的重要保障。
- 导线状态的评估需要考虑导线的材料、直径、长度、跨距、环境温
度等因素。
- 导线状态的评估需要借助弧垂分析等手段，对导线的状态进行全面、准确的评估。
5. 导线状态的调整
- 当导线状态不符合要求时，需要采取相应的调整措施。
- 导线状态的调整可以通过调整张力、增加支点、更换导线等方式实现。
- 导线状态的调整需要根据具体情况进行，以保障导线的安全性和使
用寿命。
![[架线]导地线各种弧垂的含义及计算方法（附计算表格），彻底弄懂弧垂](https://img.taocdn.com/s1/m/d68a65cb185f312b3169a45177232f60ddcce7e5.png)
[架线]导地线各种弧垂的含义及计算方法（附计算表格），彻底弄懂弧垂01-导地线各种弧垂的含义弧垂，又叫弛度，行业外叫“挠度”。
一般定义为：导线悬挂曲线上任意一点到两侧悬挂点连线之间的垂直距离（即任意点弧垂）。
在工程设计、施工、运行中，涉及到观测弧垂、竣工弧垂、平视弧垂（分小平视弧垂和大平视弧垂）、任意点弧垂、最大弧垂、中点弧垂和百米弧垂等诸多术语。
我们施工平时常用的弧垂，有观测弧垂、竣工弧垂、百米弧垂。
为方便初学者使用，将各种弧垂的含义逐一解释如下。
1）观测弧垂，就是某一温度下，现场观测时需要达到的弧垂。
高差不大的情况下，观测弧垂=竣工弧垂，只有连续倾斜地形工况下，才需要区分观测弧垂和竣工弧垂。
施工时，需要根据设计图纸要求，先计算竣工弧垂，然后根据计算出来的竣工弧垂，进一步计算出观测弧垂和线夹安装位置调整值（俗称“爬山值”）。
当导地线弧垂稳定达到观测弧垂时，停止紧线，开始进行附件安装，直线塔附件安装时，需要对线夹安装位置进行调整，也就是说线夹安装的位置不一定是导线与滑车的中心，正常线夹安装完毕，悬垂串应呈竖直状态，各档的弧垂由观测弧垂值变成竣工弧垂值。
观测弧垂、紧线弧垂、施工弧垂，基本上都是同一个意思。
孤立档的观测弧垂，在以前，孤立档或构架档紧线，是一端挂好耐张瓷瓶串，然后在另一端不带瓷瓶串紧线，弧垂紧到设计所规定的紧线弧垂时，再将耐张瓷瓶串挂到导线上，由于瓷瓶串自重比载往往比导线重很多，弧垂会发生变化。
紧线完毕挂耐张串前的弧垂，称之为观测弧垂、紧线弧垂或施工弧垂，两侧瓷瓶串均安装完毕后的弧垂，叫竣工弧垂。
如今的紧线施工工艺，是两端均带瓷瓶串紧线，其中一端事先压接完毕，另一端通过卡线器、钢丝绳短套临时与瓷瓶串金具连接，紧线完毕画印、断线压接，然后过牵引挂到金具上，弧垂直接定型，直接达到竣工弧垂。
2）竣工弧垂，附件安装完毕之后的弧垂值，是与观测弧垂、紧线弧垂、施工弧垂相对而言的。
通过上面观测弧垂的阐述，相信大家已经有了初步的理解。
第二章 导线张力(应力)弧垂计算第一节 导线和地线的机械物理特性与单位荷载一、导线的机械物理特性导线的机械物理特性，一般指破坏张力、弹性系数、热膨胀系数。
(一) 导线的破坏张力对导线作拉伸试验，将测得瞬时拉断力。
利用多次测量结果，可以建立一组经验公式来计算导线的瞬时拉断力。
考虑到施工和运行中导线接头、修补等因素，设计用导线破坏张力取其实测或计算瞬时拉断力T p 的95%，即 T ps =0.95T p （2-1-1） 式中 T p —导线的瞬时拉断力，N ；T ps —导线的破坏张力，N 。
（二）导线的弹性系数物体的弹性系数也称为弹性模量。
导线的弹性系数是指在弹性限度内，导线受拉力作用时，其应力与相对变形的比例系数，通过试验得出的应力-应变曲线确定，可表示为Tl T E A l A σεε===∆ （2-1-2） 式中 T —导线拉力，N ；l 、Δl —导线的原长和伸长，m ；σ—导线的应力，即单位截面的张力，σ=T/A ，N/mm ²； ε—导线的相对变形，ε=Δl/l ； A —导线的截面积，mm ²； E —导线的弹性系数，N/mm ²。
钢芯铝绞线的弹性系数按下式近似计算1s Al E mE E m+=+ （2-1-3） 式中 E Al 、E s 、E —分别为铝、钢和综合弹性系数，N/mm ²，E s =190000 N/mm ², E Al =55000 N/mm ²；m =A Al /A s —铝对钢的截面比m =A Al /A s 。
（三）导线的热膨胀系数导线温度升高1℃所引起的相对变形，称为导线的热膨胀系数，可表示为 /t αε=∆ （2-1-4）式中 ε—温度变化引起的导线相对变形，ε=Δl/l ；Δt —温度变化量，℃；α—导线的热膨胀系数，1/℃。
钢芯铝绞线的热膨胀系数的计算式为s sAl Al s Al E m E E mE ααα+=+ （2-1-5） 式中 αAl 、αs 、α—分别为铝、钢和综合热膨胀系数，1/℃。
第二章导线应力弧垂分析·导线的比载·导线应力的概念·悬点等高时导线弧垂、线长和应力关系·悬挂点不等高时导线的应力与弧垂·水平档距和垂直档距·导线的状态方程·临界档距·最大弧垂的计算及判断·导线应力、弧垂计算步骤·导线的机械特性曲线［内容提要及要求］本章是全书的重点，主要是系统地介绍导线力学计算原理。
通过学习要求掌握导线力学、几何基本关系和悬链线方程的建立；掌握临界档距的概念和控制气象条件判别方法；掌握导线状态方程的用途和任意气象条件下导线最低点应力的计算步骤；掌握代表档距的概念和连续档导线力学计算方法；了解导线机械物理特性曲线的制作过程并明确它在线路设计中的应用。
第一节导线的比载作用在导线上的机械荷载有自重、冰重和风压，这些荷载可能是不均匀的，但为了便于计算，一般按沿导线均匀分布考虑。
在导线计算中，常把导线受到的机械荷载用比载表示。
由于导线具有不同的截面，因此仅用单位长度的重量不宜分析它的受力情况。
此外比载同样是矢量，其方向与外力作用方向相同。
所以比载是指导线单位长度、单位截面积上的荷载，常用的比载共有七种，计算公式如下：1．自重比载导线本身重量所造成的比载称为自重比载，按下式计算（2-1）式中：g1—导线的自重比载，N/m.mm2；m0一每公里导线的质量，kg/km；S—导线截面积，mm2。
2．冰重比载导线覆冰时，由于冰重产生的比载称为冰重比载，假设冰层沿导线均匀分布并成为一个空心圆柱体，如图2－1所示，冰重比载可按下式计算：（2-2）式中：g2—导线的冰重比载，N/m.mm2；b—覆冰厚度，mm；d—导线直径，mm；S—导线截面积，mm2。
图2-1覆冰的圆柱体设覆冰圆筒体积为：取覆冰密度，则冰重比载为：3．导线自重和冰重总比载导线自重和冰重总比载等于二者之和，即g3＝g1+g2（2-3）式中：g3—导线自重和冰重比载总比载，N/m.mm2。
第二章导线应力弧垂分析·导线的比载·导线应力的概念·悬点等高时导线弧垂、线长和应力关系·悬挂点不等高时导线的应力与弧垂·水平档距和垂直档距·导线的状态方程·临界档距·最大弧垂的计算及判断·导线应力、弧垂计算步骤·导线的机械特性曲线［内容提要及要求］本章是全书的重点，主要是系统地介绍导线力学计算原理。
通过学习要求掌握导线力学、几何基本关系和悬链线方程的建立；掌握临界档距的概念和控制气象条件判别方法；掌握导线状态方程的用途和任意气象条件下导线最低点应力的计算步骤；掌握代表档距的概念和连续档导线力学计算方法；了解导线机械物理特性曲线的制作过程并明确它在线路设计中的应用。
第一节导线的比载作用在导线上的机械荷载有自重、冰重和风压，这些荷载可能是不均匀的，但为了便于计算，一般按沿导线均匀分布考虑。
在导线计算中，常把导线受到的机械荷载用比载表示。
由于导线具有不同的截面，因此仅用单位长度的重量不宜分析它的受力情况。
此外比载同样是矢量，其方向与外力作用方向相同。
所以比载是指导线单位长度、单位截面积上的荷载，常用的比载共有七种，计算公式如下：1．自重比载导线本身重量所造成的比载称为自重比载，按下式计算（2-1）式中：g1—导线的自重比载，N/m.mm2；m0一每公里导线的质量，kg/km；S—导线截面积，mm2。
2．冰重比载导线覆冰时，由于冰重产生的比载称为冰重比载，假设冰层沿导线均匀分布并成为一个空心圆柱体，如图2－1所示，冰重比载可按下式计算：（2-2）式中：g2—导线的冰重比载，N/m.mm2；b—覆冰厚度，mm；d—导线直径，mm；S—导线截面积，mm2。
图2-1覆冰的圆柱体设覆冰圆筒体积为：取覆冰密度，则冰重比载为：3．导线自重和冰重总比载导线自重和冰重总比载等于二者之和，即g3＝g1+g2（2-3）式中：g3—导线自重和冰重比载总比载，N/m.mm2。
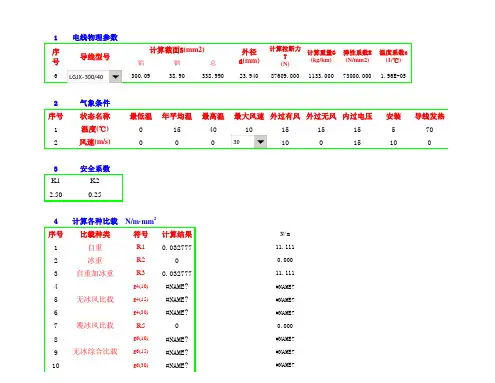
导线应力弧垂计算导线的应力弧垂计算是为了确定导线的形态以及对导线进行张力设计的重要步骤。
应力弧垂的计算能够保证导线在各种外力的作用下仍能满足导线张力、弧垂和安全等要求。
在导线应力弧垂计算中，需要考虑导线的自重、气候条件（如风速、温度等）以及拉力等因素。
下面将详细介绍导线应力弧垂计算的主要内容。
1.导线自重的计算：导线自重是导线弧垂计算的基础，需要根据导线的材料、截面形状等参数来计算。
常用的导线材料有铝、钢、镀铝钢等，不同材料的密度和弹性模量不同，对导线自重的计算产生影响。
2.外力的计算：外力包括风力、温度应力等。
风力是导线设计中最重要的外力之一，通过风压力和风速来进行计算。
可以使用一些风压公式和根据当地的气象数据来计算风力对导线的作用力。
温度应力是由于导线在高温和低温环境下的膨胀和收缩所引起的。
根据导线的线膨胀系数和温度变化范围，可以计算出温度应力对导线张力和弧垂的影响。
3.导线张力的计算：导线张力是导线应力弧垂计算中即需要考虑的因素。
导线张力通过外力和导线自重的作用来计算。
在计算过程中，需要使用悬链线理论、拉力平衡方程等公式来进行计算。
4.弧垂的计算：导线在张力作用下会形成一定的弧垂，弧垂的大小与导线自重、张力、气象因素等有关。
通过计算张力和弧垂之间的关系，可以确定导线的最佳弧垂，确保导线的安全性和可靠性。
在导线应力弧垂计算中，还要考虑导线的固定方式和绝缘子的位置、串控因素等因素对导线张力和弧垂的影响。
通过综合考虑这些因素，可以得出合理的导线应力弧垂计算结果，从而指导导线的设计、安装和维护工作。
总之，导线应力弧垂计算是非常重要的工程设计环节，直接关系到导线的安全性和可靠性。
合理的导线应力弧垂计算结果可以保证导线在各种外力的作用下保持良好的形态，从而确保电力系统的正常运行和供电质量的稳定。
第二章导线应力弧垂分析·导线的比载·导线应力的概念·悬点等高时导线弧垂、线长和应力关系·悬挂点不等高时导线的应力与弧垂·水平档距和垂直档距·导线的状态方程·临界档距·最大弧垂的计算及判断·导线应力、弧垂计算步骤·导线的机械特性曲线［内容提要及要求］本章是全书的重点，主要是系统地介绍导线力学计算原理。
通过学习要求掌握导线力学、几何基本关系和悬链线方程的建立；掌握临界档距的概念和控制气象条件判别方法；掌握导线状态方程的用途和任意气象条件下导线最低点应力的计算步骤；掌握代表档距的概念和连续档导线力学计算方法；了解导线机械物理特性曲线的制作过程并明确它在线路设计中的应用。
第一节导线的比载作用在导线上的机械荷载有自重、冰重和风压，这些荷载可能是不均匀的，但为了便于计算，一般按沿导线均匀分布考虑。
在导线计算中，常把导线受到的机械荷载用比载表示。
由于导线具有不同的截面，因此仅用单位长度的重量不宜分析它的受力情况。
此外比载同样是矢量，其方向与外力作用方向相同。
所以比载是指导线单位长度、单位截面积上的荷载，常用的比载共有七种，计算公式如下：1．自重比载导线本身重量所造成的比载称为自重比载，按下式计算（2-1）式中：g1—导线的自重比载，N/m.mm2；m0一每公里导线的质量，kg/km；S—导线截面积，mm2。
2．冰重比载导线覆冰时，由于冰重产生的比载称为冰重比载，假设冰层沿导线均匀分布并成为一个空心圆柱体，如图2－1所示，冰重比载可按下式计算：（2-2）式中：g2—导线的冰重比载，N/m.mm2；b—覆冰厚度，mm；d—导线直径，mm；S—导线截面积，mm2。
图2-1覆冰的圆柱体设覆冰圆筒体积为：取覆冰密度，则冰重比载为：3．导线自重和冰重总比载导线自重和冰重总比载等于二者之和，即g3＝g1+g2（2-3）式中：g3—导线自重和冰重比载总比载，N/m.mm2。
4．无冰时风压比载无冰时作用在导线上每平方毫米的风压荷载称为无冰时风压比载，可按下式计算：（2-3）式中：g4—无冰时风压比载，N/m.mm2；C—风载体系数，当导线直径d< 17mm时，C=1.2；当导线直径d≥17mm 时，C=1.1；v—设计风速，m/s；d—导线直径，mm；S—导线截面积，mm2；a—风速不均匀系数，采用表2－1所列数值。
表2－1各种风速下的风速不均匀系数a设计风速（m/s）20以下20-30 30-35 35以上ａ 1.0 0.85 0.75 0.70作用在导线上的风压（风荷载）是由空气运动所引起的，表现为气流的动能所决定，这个动能的大小除与风速大小有关外还与空气的容重和重力加速度有关。
由物理学中证明，每立方米的空气动能（又称速度头）表示关系为：，其中q —速度头（N／m2）,v—风速（m/s），m—空气质量（kg/m3），当考虑一般情况下，假定在标准大气压、平均气温、干燥空气等环境条件下，则每立方米的空气动能为实际上速度头还只是个理论风压，而作用在导线或避雷线上的横方向的风压力要用下式计算:式中：P h—迎风面承受的横向风荷载（N）。
式中引出几个系数是考虑线路受到风压的实际可能情况，如已说明的风速不均匀系数α和风载体型系数C等。
另外，K表示风压高度变化系数，若考虑杆塔平均高度为15m时则取1；θ表示风向与线路方向的夹角，若假定风向与导线轴向垂直时，则θ＝90°；F表示受风的平面面积（m2），设导线直径为d(mm)，导线长度为L（m），则F=dL×10-3。
由此分析则导线的风压计算式为：相应无冰时风压比载为：5．覆冰时的风压比载覆冰导线每平方毫米的风压荷载称为覆冰风压比载，此时受风面增大，有效直径为（d+2b）,可按下式计算：（2-5）式中：g5—覆冰风压比载，N/m.mm2；C—风载体型系数，取C=1.2；6．无冰有风时的综合比载无冰有风时，导线上作用着垂直方向的比载为g1和水平方向的比载为g4，按向量合成可得综合比载为g6，如图2－2所示：图2-2无冰有风综合比载则g6称为无冰有风时的综合比载，可按下式计算：（2-6）式中，g6—无冰有风时的综合比载，N/m.mm2。
7．有冰有风时的综合比载导线覆冰有风时，综合比载g7为垂直比载g3和覆冰风压比载g5向量和，如图2－3所示，图2-3覆冰有风综合比载可按下式计算：（2-6）式中g7一有冰有风时的综合比载，N/m.mm2。
以上讲了7种比载,它们各代表了不同的含义,而这个不同是针对不同气象条件而言的,在以后导线力学计算时则必须明确这些比载的下标数字的意义。
[例2-1] 有一条架空线路通过Ⅳ类气象区，所用导线为LGJ一120/20型，试计算导线的各种比载。
解：首先由书中附录查出导线LGJ一120/20型的规格参数为：计算直径d=15.07mm，铝、钢两部分组成的总截面积S=134.49mm2，单位长度导线质量m0=466.8kg/km。
由表1-8查出Ⅳ类气象区的气象条件为：覆冰厚度为b=5mm,覆冰时风速V=10m/s,最大风速V=25m/s,雷电过电压风速V=10m/s,内过电压时风速V=15m/s。
下面分别计算各种比载。
(1)自重比载g1：g1=9.80665 ×m0/S ×10-3=9.80665×466.8/134.49×10-3=34.04×10-3[N/m.mm2](2)覆冰比载g2：g2(5)=27.728×b(d+b) /S ×10-3=27.728×5(15.07+5)/134.49 ×10-3=20.69×10-3[N/m.mm2](3)垂直比载g3：g3(5)=g1+g2(5)=54.73×10-3[N/m.mm2](4)无冰时风压比载g4：由表2-1查出当风速为20～30m/s时，α=0.85，当风速为20m/s以下时，α=1.0，风载体形系数C=1.2,由公式计算g4(10)=0.6128×1.0×1.2×102/134.49×15.07×10-3 =8.24×10-3[N/m.mm2]g4(15)=0.6128×1.0×1.2×152/134.49×15.07×10-3=18.54×10-3[N/m.mm2]g4(25)=0.6128×1.0×1.2×252/134.49×15.07×10-3=43.77×10-3[N/m.mm2](5)覆冰时风压比载g5：由表1-2查出α=1.0，已知C=1.2，则g5(5,10)=0.6128×1.0×1.2(15.07+2×5)×102/S×10-3=13.71×10-3[N/m.mm2](6)无冰时综合比载g6：几种风速下的比载由公式计算,分别为(7)覆冰时综合比载g7：当重力加速度采用9.8值计算时，其结果只是微小差别。
第二节导线应力的概念悬挂于两基杆塔之间的一档导线，在导线自重、冰重和风压等荷载作用下，任一横截面上均有一内力存在。
根据材料力学中应力的定义可知，导线应力是指导线单位横截面积上的内力。
因导线上作用的荷载是沿导线长度均匀分布的，所以一档导线中各点的应力是不相等的，且导线上某点应力的方向与导线悬挂曲线该点的切线方向相同，从而可知，一档导线中其导线最低点应力的方向是水平的。
所以，在导线应力、弧垂分析中，除特别指明外，导线应力都是指档内导线最低点的水平应力，常用σ0表示。
关于悬挂于两基杆塔之间的一档导线，其弧垂与应力的关系，我们知道：弧垂越大，则导线的应力越小；反之，弧垂越小，应力越大。
因此，从导线强度安全角度考虑，应加大导线弧垂，从而减小应力，以提高安全系数。
但是，若片面地强调增大弧垂，则为保证带电线的对地安全距离，在档距相同的条件下，则必须增加杆高，或在相同杆高条件下缩小档距，结果使线路基建投资成倍增加。
同时，在线间距离不变的条件下，增大弧垂也就增加了运行中发生混线事故的机会。
实际上安全和经济是一对矛盾的关系，为此我们的处理方法是:在导线机械强度允许的范围内，尽量减小弧垂，从而既可以最大限度地利用导线的机械强度，又降低了杆塔高度。
导线的机械强度允许的最大应力称为最大允许应力，用σmax表示。
架空送电线路设计技术规程规定，导线和避雷线的设计安全系数不应小于2.5。
所以，导线的最大允许应力为：（2-8）式中［σmax］—导线最低点的最大允许应力，MPa；T cal—导线的计算拉断力，N;S—导线的计算面积，,σcal—导线的计算破坏应力，MPa；2.5—导线最小允许安全系数。
在一条线路的设计、施工过程中，一般说我们应考虑导线在各种气象条件中，当出现最大应力时的应力恰好等于导线的最大允许应力，即可以满足技术要求。
但是由于地形或孤立档等条件限制，有时必须把最大应力控制在比最大允许应力小的某一水平上以确保线路运行的安全性，即安全系数K＞2.5。
因此，我们把设计时所取定的最大应力气象条件时导线应力的最大使用值称最大使用应力，用σmax表示，则：（2-9）式中σmax—导线最低点的最大使用应力，MPa；K—导线强度安全系数。
由此可知，当K=2.5时，有σmax＝［σmax］，这时，我们称导线按正常应力架设；当K＞2.5时，则，这时σmax<［σmax］，我们称导线按松弛应力架设。
导线的最大使用应力是导线的控制应力之一，后边还要进行讨论。
工程中，一般导线安全系数均取2.5，但变电所进出线档的导线最大使用应力常是受变电所进出线构架的最大允许应力控制的；对档距较小的其他孤立档，导线最大使用应力则往往是受紧线施工时的允许过牵引长度控制；对个别地形高差很大的耐张段，导线最大使用应力又受导线悬挂点应力控制。
这些情况下，导线安全系数均大于2.5的，为松弛应力架设。
导线的应力是随气象条件变化的，导线最低点在最大应力气象条件时的应力为最大使用应力，则其他气象条件时应力必小于最大使用应力。
第三节悬点等高时导线弧垂、线长和应力关系二、平抛物线方程平抛物线方程是悬链线方程的简化形式之一。
它是假设作用在导线弧长上的荷载沿导线在x轴上的投影均匀分布而推出的，在这一假设下，图2-6中导线所受垂直荷载变成即用直线代替弧长，从而使积分简化，由此导出平面抛物方程为（2－17）相应导线的弧长方程式为：（2－18）实际上式(2-17)是式(2-14)取前一项的结果，式(2-18)是式(2-16)取前两项的结果，这恰说明它是悬链线方程的近似表达式。
