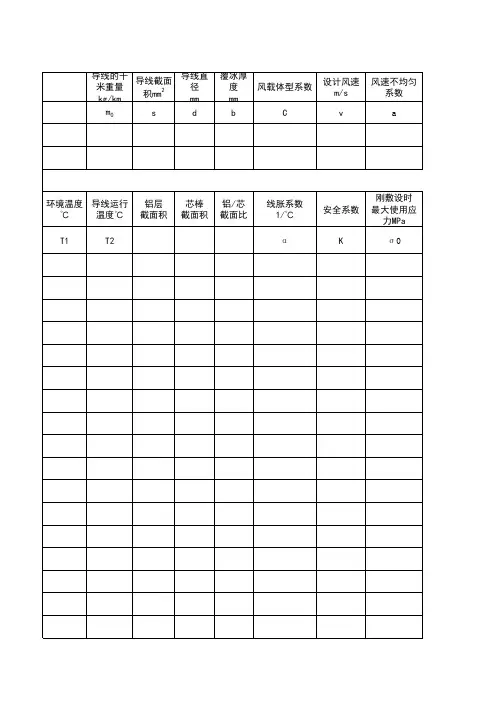
LGJ15020线应力弧垂计算表

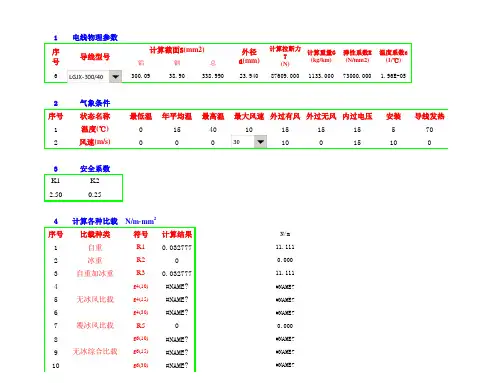
放线张力弧垂表(多功能)

风速不均匀系数α
#NAME?
#NAME?
#NAME?
空气动力系数K
#NAME?
#NAME?
#NAME?
N/m 11.111 0.000 11.111 #NAME? #NAME? #NAME? 0.000 #NAME? #NAME? #NAME?
11 覆冰综合比载
R7
0
0.000
5 计算临界档距
温度系数c (1/℃)
87609.000 1133.000 73000.000 1.96E-05
最低温 0 0
年平均温 15 0
最高温 40 0
最大风速外过有风外过无风内过电压
10
15
15
15
30
10
0
15
2
安装 5 10
#NAME?
#NAME?
导线发热 70 0
4 序号
1 2 3 4 5 6 7 8 9 10
6
覆冰冰厚mm 160 ##### #NAME? #NAME? #NAME? #NAME?
7
0
0
170 ##### #NAME? #NAME? #NAME? #NAME?
8
0
180 ##### #NAME? #NAME? #NAME? #NAME?
9
190 ##### #NAME? #NAME? #NAME? #NAME?
计算各种比载比载种类自重冰重自重加冰重
无冰风比载
覆冰风比载
无冰综合比载
N/m·mm2
符号计算结果
R1 0.032777
R2
0
R3 0.032777
g4(10)

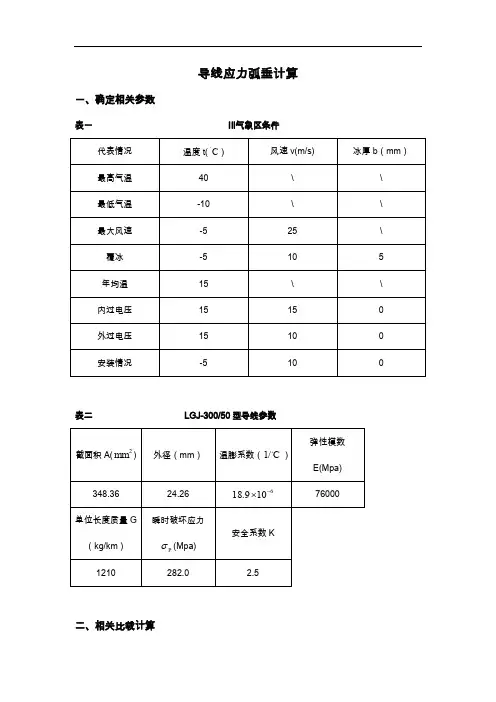
导线应力弧垂计算

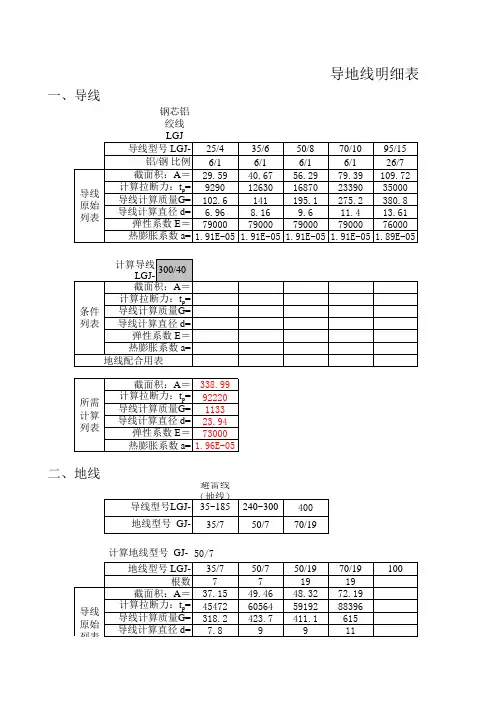
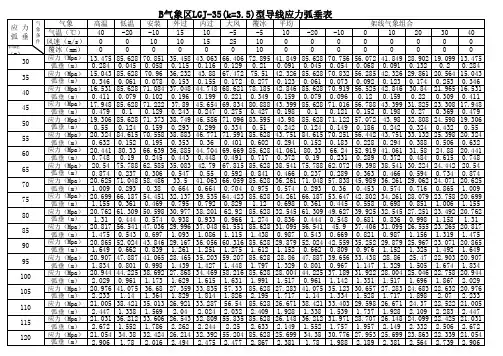
导线应力弧垂计算一、确定相关参数表一Ⅲ气象区条件表二LGJ-300/50型导线参数二、相关比载计算1. 自重比载)/(1006.341036.34880665.912100,0331m Mpa A qg --⨯=⨯⨯==）（γ2. 冰重比载)/(1060.111036.348)26.245(5728.2710)(728.270,53332m Mpa A b d b ---⨯=⨯+⨯⨯=⨯+=）（γ3.垂直总比载)/(1066.45050,00,53213m Mpa -⨯=+=），（）（）（γγγ 4.无冰风压比载5.626.1106.122===V W V (Pa) 63.3906.1256.122===V W V (Pa)1）外过电压、安装有风： 33241036.3485.6226.241.185.00.110sin 10,0--⨯⨯⨯⨯⨯=⨯=θμαβγA W d v sc f c ）（ =4.103-10⨯（Mpa/m ）2）最大设计风速：计算强度：33241036.34863.39026.241.185.00.110sin 25,0--⨯⨯⨯⨯⨯=⨯=θμαβγA W d v sc f c ）（=25.433-10⨯（Mpa/m ）低于500kv 的线路c β取1.0，计算强度时f α按表取0.85，当d ≥17mm 时sc μ取1.1.计算风偏：33241036.34863.39026.241.175.00.110sin 25,0--⨯⨯⨯⨯⨯=⨯=θμαβγA W d v sc f c ）（ =22.443-10⨯（Mpa/m ）计算风偏时f α取0.75 3）内过电压：625.1406.1156.122===V W V (Pa) 33241036.348625.14026.241.185.00.110sin 15,0--⨯⨯⨯⨯⨯=⨯=θμαβγA W d v sc f c ）（ =9.163-10⨯（Mpa/m ）5. 覆冰风压比载5.626.1106.122===V W V 32510sin )2(10,5-⨯+=θμαβγAW b d B vsc f c ）（ 3-1036.3485.621026.241.12.10.10.1⨯⨯+⨯⨯⨯⨯=）（）（m Mpa /1011.83-⨯=6. 无冰综合比载外过电压、安装有风：)/(1031.341010.406.3410,00,025,033-2224216m Mpa -⨯=⨯+=+=）（）（）（γγγ 最大设计风速（计算强度）：)/(1051.421043.2506.3425,00,025,033-2224216m Mpa -⨯=⨯+=+=）（）（）（γγγ 最大设计风速（计算风偏）：)/(1079.401044.2206.3425,00,025,033-2224216m Mpa -⨯=⨯+=+=）（）（）（γγγ内过电压：)/(1027.351016.906.345.12,00,010,033-2224216m Mpa -⨯=⨯+=+=）（）（）（γγγ7. 覆冰综合比载)/(1037.4610,50,510,5325237m Mpa -⨯=+=）（）（）（γγγ表三比载三、确定应力值（1）最大使用应力:)(8.1125.20.282Mpa kp===σσ （2）年平均运行应力上线：)(5.70%250.282%25][Mpa p pj =⨯=⨯=σσ四、计算临界档距，判断控制气象条件因为覆冰与最大风情况下的最大使用应力和气温都相同，又覆冰时的比载大于最大风时的比载，故最大风不再作为控制气象图条件考虑。

弧垂计算及k值计算

18.9 73000
18.88 76000
21.6 73000
1.85E-05 1.89E-05 1.85E-05 1.96E-05 1.89E-05 1.96E-05 1.89E-05 1.96E-05
240/40 300/25 300/40 400
24/7
48/7
24/7
277.75 83370 964.3
一、导线
导线原始列表
导地线明细表
钢芯铝
绞线
LGJ
导线型号 LGJ- 25/4
35/6
50/8 70/10 95/15
铝/钢比例 6/1
6/1
6/1
6/1
26/7
截面积：A＝ 29.59 40.67 56.29 79.39 109.72
计算拉断力：tp= 9290 导线计算质量G= 102.6
12630 141
16870 195.1
23390 275.2
35000 380.8
导线计算直径 d= 6.96
8.16
9.6
11.4 13.61
弹性系数 E＝ 79000 79000 79000 79000 76000
热膨胀系数 a= 1.91E-05 1.91E-05 1.91E-05 1.91E-05 1.89E-05
弹性系数 E＝ 181423 热膨胀系数 a= 1.15E-05
线明细表
95/20 120/20 120/25 150/20 150/25 185/25 185/30 240/30
7/7
26/7
7/7
24/7
26/7
24/7
26/7
24/7
113.96 37200 408.9

导线应力弧垂表

55
应力（Mpa） 20.324 84.615 70.558 38.883 46.771 71.591 85.628 43.751 84.615 70.251 56.442 43.751 33.132 25.398 20.324 弧垂（m） 0.632 0.152 0.195 0.353 0.36 0.401 0.602 0.294 0.152 0.183 0.228 0.294 0.388 0.506 0.632
65
应力（Mpa） 20.54 75.788 62.585 35.083 42.79 67.815 85.628 38.541 75.788 62.072 49.398 38.541 30.224 24.442 20.54 弧垂（m） 0.874 0.237 0.306 0.547 0.55 0.592 0.841 0.466 0.237 0.289 0.363 0.466 0.594 0.734 0.874
B气象区LGJ-35(k=3.5)型导线应力弧垂表
应力弧垂
气
气象
象条
气温（℃）
件风速（m/s）
高温 40 0
低温 -20 0
安装 -10 10
外过 15 10
内过 10 15
大风 -5 25
覆冰 -5 10
平均 10 0
-20 0
-10 0
架线气象组合
0
10
20
0
0
0
30 0
40 0
档距（m）
110
应力（Mpa） 21.005 38.421 35.013 26.921 33.287 56.54 85.628 26.671 38.421 33.403 29.598 26.671 24.37 22.522 21.005 弧垂（m） 2.447 1.338 1.569 2.04 2.024 2.032 2.409 1.928 1.338 1.539 1.737 1.928 2.109 2.283 2.447

导线比载及应力弧垂计算表

导线比载计
导线的千导线截面导线直米重量径积mm2 kg/km mm m0 s d 覆冰厚度 mm b 风载体型系数 C 设计风速 m/s v 风速不均匀系数 a
导线应力弧垂
环境温度导线运行 ℃ 温度℃ T1 T2 铝层截面积芯棒截面积铝/芯截面比线胀系数 1/℃ α 安全系数 K 刚敷设时最大使用应力MPa σ0
导线比载计自重与冰重总比无冰时风压比载覆冰时风压比载载 N/km·mm2 N/km·mm2 2 N/km·mm g3 g4 g5
导线应力弧垂计算表
档距 m l 刚敷设时最大弧垂 m f 刚敷设时线长 m L 导线悬挂点应力 Mpa σ A=σ B 施工后线长 m L
无冰有风综合比载 N/km·mm2 g6
有冰有风时综合比载 N/km·mm2 g7
施工后弧垂 m f
施工后应力 Mpa σ0

计算机在输电线路导线、避雷线弧垂应力计算中的应用(1)

计算机在输电线路导线、避雷线弧垂应力计算中的应用摘要架空输电导线、避雷线的弧垂，在实际工程中是非常重要的，这是因为架空线常年暴置于大自然中，受气象条件的影响较大，当温度变化或外部荷载大小变化时，架空线的长度会发生改变，虽然与其实际长度相比较其所占的百分比很小，但架空线长度的很小变化，会引起导线弧垂和应力产生相当大的变化。

在线路设计中，若设计弧垂过小，架空线收得过紧，则会引起应力过大，振动加剧，同时杆塔荷载增大因而要求强度提高。

反之，若弧垂过大，架空线较松弛，则为了满足导线对地的安全距离要求，需增加杆塔的高度和增大杆塔头部尺寸，使线路投资增加。

因此，弧垂的理论研究和计算，已成为输电线路设计和施工的重要理论计算工作之一。

特别是近几年来，我国超高压交、直流输电线路的迅速发展，越来越多地使用大载面导线或分裂导线，档距也越来越大，所以更应该进一步去研究弧垂计算理论，计算出更精确的弧垂数值来。

本文从阐述在线路设计过程中的所涉及的架空线弧垂应力、不平衡张力及荷载计算等方面的理论、概念及计算方法等入手，其中重点是导线、避雷线弧垂应力计算方面。

并通过结合计算机技术的应用进行算例，从中体现出计算机技术在线路设计繁杂的计算中应用的优越性。

关键字：计算机，线路计算，应用目录引言 (1)1.导线、避雷线弧垂应力1.1 概述 (2)1.2 设计用气象条件 (2)1.3 导线、避雷线的比载计算 (2)1.4 架空线的最大使用应力和年平均应力 (4)1.5 临界档距 (4)1.5.1 临界档距的概念 (5)1.5.2 临界档距的计算公式 (6)1.5.3 临界档距的判定 (7)1.6 最大弧垂的判定 (7)1.7 弧垂应力曲线计算及制作 (8)1.7.1 设计线路概况 (8)1.7.2 导线弧垂应力曲线计算及制作 (9)1.7.3 避雷线弧垂应力曲线计算及制作 (17)1.8 弧垂应力计算语言、自设程序 (22)2.避雷线最大使用应力的确定2.1 简述 (25)2.2 避雷线最大使用应力的选择 (25)3.导线、避雷线不平衡张力计算3.1 概述 (26)3.2 断线张力的确定 (26)3.3 线路正常运行中的不平衡张力计算 (27)3.4 避雷线的支持力 (27)4.杆塔荷载的计算4.1 荷载的分类和荷载组合 (27)4.2 荷载的计算条件 (28)4.3 荷载计算用档距的确定 (29)4.4 荷载的计算 (29)结论 (30)参考文献 (30)附件 (30)引言架空线常年暴置于大自然中，经受各种恶劣气候的影响。

弧垂表(LGJ、JKLGYJ等全型号)

8618.7 7714.6 6833.3 0.134 0.150 0.170
5188.3 4460.5 3823.4 3290.8 2862.5 2525.3 0.223 5239 0.273 0.260 0.303 0.352 0.405 3017 0.474 0.459 2688.1 0.532
7931.2 7355.9 6833.3 6363.1 5943.1 5569.6 5238.4 4944.9 4684.4 4452.7 1.219 1.315 1.415 1.520 1.627 6006 1.867 1.736 1.846 1.956 2.064 4821 2.326 2.172
8357.4 7571.3 6833.3 6153.6 5540.7 4999.9 4531.5 4131.3 3791.8 3504.5 3260.6 3052.5 2873.7 0.438 0.484 0.536 0.595 0.661 0.732 0.808 0.886 0.966 1.045 1.123 1.200 1.274
2 2
C
K=6.00 134.29 15.1 4.58 76000
电线物理特性数据：线膨胀系数（1/℃）瞬时破坏应力（N/mm ）最大使用应力（N/mm2）平均运行应力（N/mm2）
2
18.9 × -6 10 305.3094 50.8849 76.3274
比载(N/m· ) mm
2
g1= பைடு நூலகம்.0341
2052.1 1884.4 0.565 2215.4 0.646 2371 0.730 0.615 2044 0.700 2196.9 0.788
8271.5 7526.3 6833.3 6200.5 5633.2 5133.3 4698.9 4324.6 4003.7 3728.5 3491.8 3287.2 3109.3 A 0.560 0.616 0.678 0.748 0.823 0.903 0.986 1.072 1.158 1.243 1.327 1.410 1.491

导线弧垂计算

40 20 弧 30 10 垂 20 0 系
10 -10 数 0 -20
-10 -30
50 0.176 0.143 0.12
0.103 0.9 0.8
100 0.69 0.577 0.491
0.424 0.372 0.331
150 1.523 1.221 1.146
1.001 0.882 0.785
插值计算 300
0.739
325
312
0.727 0.73612
对应代
表档距
下的弧
垂系数
H/L K
（0.1 7）
0℃
0.014 4.305
0.031 4.305
-0.03 7.504
0.209 0.377
-0.05 11.024
-0.12 0.372
-0 2.804
0.032 2.804
10℃
4.685 4.685 7.064 0.43 11.532 0.424 3.104 3.104
65.96 9.17 90.70 0.60 305.47 0.34 26.80 7.94
高程
呼称高
高差H
30℃ 小号大号小号大号
71.59 9.90 83.94 0.71 325.07 0.40 29.52 8.74
426 416 18 416 404 21 404 413 18 413 387 21 387 416 24 416 426 18 426 424 18 424 410 21
21
7
18 15
21 -12
24 23
18 -23
18 -10
21 -1
21 14
803 516
354

架线弧垂计算表(应力弧垂插值计算)

1
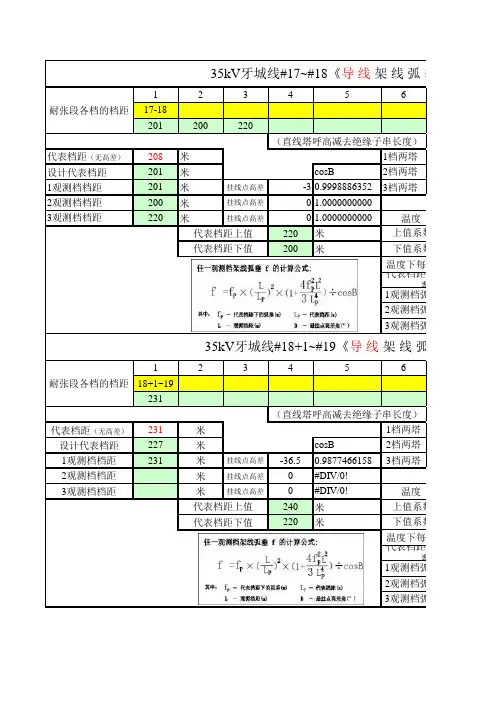
23456
17-18201
200
220
代表档距（无高差）208米1档两塔
设计代表档距201米cosB 2档两塔1观测档档距201米挂线点高差-30.99988863523档两塔
2观测档档距200米挂线点高差01.00000000003观测档档距
220
米
挂线点高差
01.0000000000220米200
米
1
23456
18+1~19
231
代表档距（无高差）231米1档两塔
设计代表档距227米cosB
2档两塔1观测档档距231
米挂线点高差-36.50.98774661583档两塔
2观测档档距米
挂线点高差
0#DIV/0!3观测档档距
米
挂线点高差0#DIV/0!240米220
米
耐张段各档的档距
耐张段各档的档距35kV 牙城线#18+1~#19《导线架线弧垂表/应力弧
35kV 牙城线#17~#18《导线架线弧垂表/应力弧
温度下每米的代表档距的弧
数
1观测档弧垂（m ）2观测档弧垂（m ）3观测档弧垂（m ）（直线塔呼高减去绝缘子串长度）
温度（℃代表档距上值
上值系数（m ）代表档距下值
下值系数（m ）温度下每米的代表档距的弧
数
1观测档弧垂（m ）2观测档弧垂（m ）3观测档弧垂（m ）（直线塔呼高减去绝缘子串长度）
温度（℃代表档距上值上值系数（m ）代表档距下值
下值系数（m ）
架线架线弧。

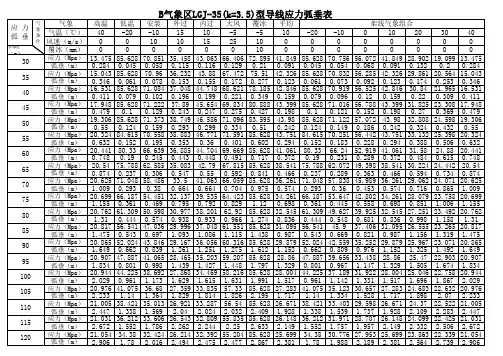
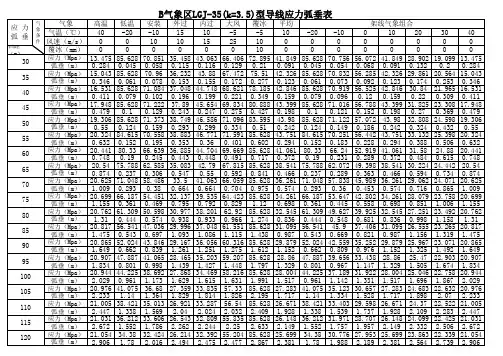
导线应力弧垂表

线规截面（mm²）
单位质量（kg/m）最大使用应力（Mpa ）平均运行应力（Mpa ）
计算条件
LGJ-35 56.29 外径（mm）
0.2 拉断力（kN）
9.6 16.87
85.63
安全系数
3பைடு நூலகம்5
53.95
取用系数
18%
气象高温低温安装外过内过大风覆冰平均
气象条件
B气象区LGJ-35(k=3.5)型导线应力弧垂表
应力弧垂
气
气象
象条
气温（℃）
件风速（m/s）
高温 40 0
低温 -20 0
安装 -10 10
外过 15 10
内过 10 15
大风 -5 25
覆冰 -5 10
平均 10 0
-20 0
-10 0
架线气象组合
0
10
20
0
0
0
30 0
40 0
档距（m）
50
应力（Mpa） 19.306 85.628 71.373 38.749 46.586 71.096 83.595 43.98 85.628 71.122 57.072 43.98 32.808 24.598 19.306 弧垂（m） 0.55 0.124 0.159 0.293 0.299 0.334 0.51 0.242 0.124 0.149 0.186 0.242 0.324 0.432 0.55
40
应力（Mpa） 16.531 85.628 71.084 37.048 44.748 68.621 78.185 42.846 85.628 70.919 56.525 42.846 30.84 21.965 16.531 弧垂（m） 0.411 0.079 0.102 0.196 0.199 0.221 0.349 0.159 0.079 0.096 0.12 0.159 0.22 0.309 0.411

导线应力弧垂表

比载[×10-3N过大风覆冰平均水平 0 0 12.791 12.791 28.78 67.952 39.439 0 垂直 33.99 33.99 33.99 33.99 33.99 33.99 130.536 33.99 综合 33.99 33.99 36.317 36.317 44.537 75.978 136.364 33.99
计算条件
线规截面（mm²） 56.29 单位质量 0.2 （kg/m）最大使用应力（Mpa）平均运行应力（Mpa） LGJ-35 外径（mm）拉断力（kN） 85.63 安全系数 53.95 取用系数 9.6 16.87 3.5 18%
气象条件
气象高温低温安装外过内过大风覆冰平均气温（℃） 40 -20 -10 15 10 -5 -5 10 风速（m/s） 0 0 10 10 15 25 10 0 冰厚（mm） 0 0 0 0 0 0 10 0
覆冰 -5 10 10 72.895 0.21 75.51 0.277 78.185 0.349 80.888 0.427 83.595 0.51 85.628 0.602 85.628 0.717 85.628 0.841 85.628 0.975 85.628 1.12 85.628 1.274 85.628 1.438 85.628 1.612 85.628 1.797 85.628 1.991 85.628 2.195 85.628 2.409 85.628 2.633 85.628 2.867
架线气象组合 0 10 20 0 0 0 0 0 0 56.072 41.849 28.902 0.068 0.091 0.132 56.285 42.326 29.861 0.092 0.123 0.174 56.525 42.846 30.84 0.12 0.159 0.22 56.788 43.399 31.825 0.152 0.198 0.27 57.072 43.98 32.808 0.186 0.242 0.324 56.442 43.751 33.132 0.228 0.294 0.388 52.919 41.061 31.58 0.289 0.372 0.484 49.398 38.541 30.224 0.363 0.466 0.594 45.989 36.261 29.062 0.453 0.574 0.716 42.802 34.261 28.079 0.558 0.698 0.851 39.925 32.545 27.251 0.681 0.836 0.998 37.406 31.095 26.555 0.821 0.987 1.156 35.252 29.879 25.967 0.976 1.152 1.325 33.438 28.86 25.47 1.147 1.329 1.505 31.922 28.004 25.046 1.331 1.517 1.696 30.657 27.283 24.683 1.528 1.717 1.898 29.598 26.671 24.37 1.737 1.928 2.109 28.707 26.148 24.099 1.957 2.149 2.332 27.953 25.699 23.863 2.189 2.381 2.564

120弧垂表

195 200 205 210 215 220 225 230 235 240 245 250 255 260 265 270 275 280 285 290
30.95 37.57 76.21 60.67 35.51 31.00 37.24 76.21 60.60 35.37 31.04 36.94 76.21 60.53 35.23 31.07 36.66 76.21 60.47 35.11 31.11 36.41 76.21 60.42 34.99 31.14 36.18 76.21 60.36 34.89 31.17 35.96 76.21 60.31 34.79 31.20 35.76 76.21 60.26 34.69 31.22 35.58 76.21 60.22 34.61 31.25 35.41 76.21 60.18 34.52 31.27 35.25 76.21 60.14 34.45 31.30 35.10 76.21 60.10 34.38 31.32 34.96 76.21 60.07 34.31 31.34 34.83 76.21 60.03 34.25 31.36 34.71 76.21 60.00 34.19 31.37 34.60 76.21 59.97 34.13 31.39 34.49 76.21 59.94 34.08 31.41 34.39 76.21 59.92 34.03 31.42 34.29 76.21 59.89 33.98 31.44 34.20 76.21 59.87 33.94
90 95 100 105 110 115 120 125 130 135 140 145 150 155 160 165 170 175 180 185 190
28.54 72.05 76.21 64.87 47.68 28.79 67.77 76.21 64.43 46.09 29.02 63.80 76.21 64.03 44.70 29.23 60.21 76.21 63.67 43.50 29.41 57.02 76.21 63.35 42.46 29.58 54.22 76.21 63.05 41.55 29.73 51.80 76.21 62.78 40.75 29.87 49.70 76.21 62.54 40.06 30.00 47.90 76.21 62.32 39.45 30.11 46.34 76.21 62.12 38.91 30.22 44.99 76.21 61.93 38.44 30.32 43.83 76.21 61.77 38.01 30.40 42.81 76.21 61.61 37.63 30.49 41.92 76.21 61.47 37.29 30.56 41.13 76.21 61.34 36.99 30.63 40.44 76.21 61.22 36.71 30.70 39.82 76.21 61.11 36.47 30.75 39.27 76.21 61.01 36.24 30.81 38.78 76.21 60.92 36.03 30.86 38.34 76.21 60.83 35.84 30.91 37.93 76.21 60.75 35.67

应力、弧垂分析方法

总结前述应力、弧垂分析方法，导线的应力、弧垂计算步骤以下面例题作进一步说明：［例2-5］某35KV输电线路，导线为LGJ-95/20型，全国第Ⅱ气象区，安全系数K=2.5，采用防振锤防振，其中年平均运行应力为σpcal=0.25σcal，在线路中有一耐张段布置如图2-19所示，试求以下内容：(1)第二档中交叉跨越通信线的垂直距离能否满足要求？(2)＃4杆塔的最大、最小垂直档距以及最大上拔力是多少？图2-19某耐张段布置图解：该题中并未告知计算气象条件及应力。

通过计算分析可明确本章各节内容的相互联系及应用方法，计算时可按如下步骤：1.计算临界档距并判别控制区；2.计算代表档距，确定本耐张段的控制条件；3.确定计算气象条件并计算各计算气象条件时的应力；4.进行各具体项目的计算。

(1)计算临界档距并判别控制条件导线物理特性参数如下：弹性系数E=7600MPa；截面积S=113.9mm2；热膨胀系数α=18.5×10-61/℃；外径d=13.87mm；计算拉断力T cal=37200N。

则瞬时破坏应力最大使用应力年平均运行应力将有关计算数据列于下表2-6中。

将有关数据代入临界档距计算式，可计算得各临界档距值如表2-7所示。

=虚数CBC=500.30 CCD=298.87CAB=126.11 CBD=362.35CAC=203.63CAD有效临界档距判别结果见图2-20所示，图2-20有效临界档距判别结果即有：当，控制条件为年平均气温，年平均运行应力；当，控制条件为最大风速，最大使用应力。

(2)计算代表档距=245.06（m）结合有效临界档距判别结果可知，该耐张段应力计算控制气象条件为年平均气温，控制应力。

(3)交叉跨越校验和垂直档距计算1)交叉跨越校验交叉跨越校验应按最大垂直弧垂气象条件进行。

首先应用状态方程式求出高温时或最大垂直比载时的应力。

然后进行最大垂直弧垂判别，最后计算弧垂。

具体参见书56页计算过程。

LGJ15020线应力弧垂计算表

合集下载

放线张力弧垂表(多功能)

导线应力弧垂计算

弧垂计算及k值计算

导线应力弧垂表

导线比载及应力弧垂计算表

计算机在输电线路导线、避雷线弧垂应力计算中的应用(1)

弧垂表(LGJ、JKLGYJ等全型号)

导线弧垂计算

架线弧垂计算表(应力弧垂插值计算)

导线应力弧垂表

导线应力弧垂表

120弧垂表

应力、弧垂分析方法

文档推荐

最新文档