耐克函数的图象及性质优秀PPT
- 格式:ppt
- 大小:1.10 MB
- 文档页数:16

课题研究——对于“耐克函数”的研究经过小组研究,现发现形如xb ax y +=(a>0,b>0) 的函数有如下的特点:即x=1时最小值为2.当给出的定义域区间不包括耐克函数的顶点时,求最值应该利用耐克函数的单调性来解。
如下面这个例子 例.求函数324222++++=x x x x y 的最小值。
解:令322++=x x t ,则22)1(2≥++=x ttt tt y 112+=+=根据对号函数tt y 1+=在(1,+∞)上是增函数及t 的取值范围,当2=t 时y有最小值223。
此时x=-1.此题是一道求最值的问题,由于t ≥2,所以不能用均值不等式t+t1≥2来解,所以用耐克函数的单调性来解比较简易。
例 已知函数],1[,2)(2+∞∈++=x xax x x f 。
(1) 当21=a 时,求函数)(x f 的最小值:Oxyxy =221解:(1)2)(21++=xx x f设xx x g 21)(+= [)+∞∈,1x ,其图象如图所示, 在[)+∞,1上是增函数,当1=x 时,23)(m in =x g27)(m in =x f面对这个函数 f(x)=ax+b/x , 我们应该想得更多,需要我们深入探究:(1)它的单调性与奇偶性有何应用?而值域问题恰好与单调性密切相关,所以命题者首先想到的问题应该与值域有关;(2)函数与方程之间有密切的联系,所以命题者自然也会想到函数与方程思想的运用;(3)众所周知,双曲线中存在很多定值问题,所以很容易就想到定值的存在性问题。
因此就由特殊引出了一般结论;继续拓展下去,用所猜想、探索的结果来解决较为复杂的函数最值问题。



函数的图像与性质课件函数是数学中一个非常重要且广泛应用的概念。
它将输入值映射到输出值,可以用图像来直观地表示函数的性质。
本课件将介绍函数的图像与性质,帮助读者更好地理解和应用函数。
一、函数的定义与图像表示函数是一种特殊的关系,它将一个集合中的每个元素都对应到另一个集合中的唯一元素上。
数学上常用的表示函数的方式有函数符号法、图像法和映射关系法。
其中,图像法是最直观且常用的一种方式。
图像法通过将函数的输入值和输出值表示在坐标系中,从而形成一个函数的图像。
在直角坐标系中,横轴表示输入值,纵轴表示输出值,将函数的所有点连接起来,就得到了函数的图像。
函数图像可以帮助我们观察函数的性质,如增减性、奇偶性等。
二、常见函数的图像与性质1. 线性函数线性函数是函数中最简单且最重要的一类函数。
它的图像呈现为一条直线,表达式为y=ax+b,其中a和b是常数。
线性函数的特点是斜率恒定,图像可以通过斜率和截距来确定。
2. 幂函数幂函数是一类以自变量为底数的函数,常见的有平方函数、立方函数等。
幂函数的图像呈现为一条曲线,其形状受幂指数的正负和大小的影响。
根据幂指数的奇偶性,可以确定幂函数的对称性。
3. 指数函数指数函数是以指数为变量的函数,常见的有以e为底的自然指数函数。
指数函数的特点是增长速度快,图像在原点处必过(0,1),具有递增性质。
4. 对数函数对数函数是指以某个正常数为底数的函数,常见的有自然对数函数。
对数函数的图像在正半轴递增,并且在(1,0)处必过,具有递增性质。
5. 三角函数三角函数是以角度或弧度为自变量的函数,常见的有正弦函数、余弦函数等。
三角函数的图像周期性重复出现,并且具有交替性。
三、函数图像的应用函数图像不仅能够直观地展示函数的性质,还有很多实际应用。
以下是一些常见的应用领域:1. 物理学中的运动轨迹函数图像可以用于描述物体在不同时间的位置变化情况,常见的有抛物线轨迹、圆周运动等。
2. 经济学中的供需关系函数图像可以用于表示市场的供给和需求关系,帮助分析市场的平衡点和价格变化。


耐克函数和韦达定理耐克函数,又称双曲函数,双勾函数。
是形如f(x)=ax+b/x(a>0)的函数。
当x>0时,f(x)=ax+b/x有最小值(这里为了研究方便,规定a>0,b>0),也就是当x=sqrt(b/a)时(sqrt表示求二次方根)。
韦达定理证明了一元n次方程中根和系数之间的关系。
这里讲一元二次方程的根与系数的关系。
定理内容:一元二次方程中,两根x₁、x₂有如下关系由一元二次方程求根公式为:(注意:a指二次项系数,b指一次项系数,c指常数,且a≠0)可得,1.2.家教——三角函数公式大全两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- sin2A=2s inA•cosA cos2A = cos 2A-sin 2A=2cos 2A-1=1-2sin 2A 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=AA cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 和差化积sina+sinb=2sin2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2ba - cosa+cosb = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)]万能公式sina=2)2(tan 12tan 2a a + cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan2aa - 其它公式a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab]a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba]平面向量--02/08一、选择题错误!未指定书签。

定义对勾函数是一种类似于反比例函数的一般函数,又被称为“双勾函数”、"勾函数"等。
也被形象称为“耐克函数”所谓的对勾函数(双曲线函数),是形如f(x)=ax+b/x 的函数。
由图像得名。
图像对勾函数:图像,性质,单调性对勾函数是数学中一种常见而又特殊的函数,见图示。
奇偶性与单调性当x>0时,f(x)=ax+b/x有最小值(这里为了研究方便,规定a>0,b>0),也就是当x=sqrt(b/a)的时候(sqrt表示求二次方根)奇函数。
令k=sqrt(b/a),那么:增区间:{x|x≤-k}和{x|x≥k};减区间:{x|-k≤x<0}和{x|0<x≤k} 变化趋势:在y 轴左边,增减,在y轴右边,减增,是两个勾。
渐近线耐克函数的图像是分别以y轴和y=ax为渐近线的两支双曲线。
编辑本段均值不等式对勾函数性质的研究离不开均值不等式。
说到均值不等式,其实也是根据二次函数得来的。
我们都知道,(a-b)^2≥0,展开就是a^2-2ab+b^2≥0,有a^2+b^2≥2ab,两边同时加上2ab,整理得到(a+b)^2≥4ab,同时开根号,就得到了平均值定理的公式:a+b≥2sqrt(ab)。
现在把ax+b/x套用这个公式,得到ax+b/x≥2sqrt(axb/x)=2sqrt(ab),这里有个规定:当且仅当ax=b/x时取到最小值,解出x=sqrt(b/a),对应的f(x)=2sqrt(ab)。
我们再来看看均值不等式,它也可以写成这样:(a+b)/2≥sqrt(ab),前式大家都知道,是求平均数的公式。
那么后面的式子呢?也是平均数的公式,但不同的是,前面的称为算术平均数,而后面的则称为几何平均数,总结一下就是算术平均数绝对不会小于几何平均数。
这些知识点也是非常重要的。
编辑本段导数求解其实用导数也可以研究对勾函数的性质。
不过首先要会负指数幂的换算,这也很简单,但要熟练掌握。

一次双勾函数1、定义:由于它的图像在直角坐标系中的形状大致像两个对称的“双勾”而得名。
故又称“双勾函数”、“打勾函数”、“对勾函数”、“耐克函数”等。
2、类型:⑴、一次双勾:函数x bax x f y +==)( 0(>a ,)0>bA 、基本性质:①、定义域:{0≠x x 且x R ∈};②、值域:{ab y y 2≥ 或y ab 2-≤};③、奇偶性:由)()(x f x f -=-得,此函数为奇函数; ④、单调性:y 轴的左侧:增、减;y 轴的右侧:减、增;单调递增区间为⎥⎦⎤ ⎝⎛-∞-a b ,和⎪⎪⎭⎫⎢⎣⎡+∞,a b , 单调递减区间为⎪⎪⎭⎫⎢⎣⎡-0,a b 和⎥⎦⎤⎝⎛a b ,0 注意:不可写成并集形式:⎥⎦⎤⎝⎛⎪⎪⎭⎫⎢⎣⎡-a b a b ,00, ⑤、渐近线:ax y =,和0=x证明: ∵ xbax x f +=)(, 当→∝x 时,ax x f →)(, ∴ax y =是渐近线。
⑥、对称轴:ax y 2=B 、图像特点:①、 当0>x 时,图像在第一像限以⎪⎪⎭⎫⎝⎛ab a b 2,为顶点, 开口向上,在⎥⎦⎤⎝⎛a b ,0上是减函数, 在⎪⎪⎭⎫⎢⎣⎡+∞,a b 上是增函数, y 有最小值ab 2②、 当0<x 时,图像在第三像限以⎪⎪⎭⎫ ⎝⎛--ab a b 2,为顶点, 开口向下,在⎥⎦⎤⎝⎛-∞-a b ,上是增函数, 在⎪⎪⎭⎫⎢⎣⎡-0,a b 上是减函数, y 有最大值ab 2-附:ⅰ、顶点证明:[不等式法] ∵ab xbax x b ax x f y 22)(=∙≥+== 当且仅当xbax =时等号成立,(注意:等号要能取到) 此时有最小值ab 2 另由x bax =,得a b x =∴最小值点(顶点)坐标是⎪⎪⎭⎫⎝⎛ab a b 2, [导数法]对)(x f 求导:21)()(xb a x b ax x f -=+='当0)(='x f 时有极值:01)(2=-='xb a x f ,得ab x =代入原方程得ab y 2= ∴最小值点(顶点)坐标是⎪⎪⎭⎫⎝⎛ab a b2, ⅱ、证明奇偶性:∵ 定义域为{0≠x x 且x R ∈}即),0()0,(∝+∝- ,关于原点对称。

【例题板块】a上的最大值.例如:D∈[0,【例题】若方程在有解,求实数的取值范围.0122=+-ax x ),3[+∞a ●已知函数定义在R 上.1()2x f x +=(1)若存在,使得成立,求实数的取值范围;x ()()f x f x a +-=a (2)若可以表示为一个偶函数与一个奇函数之和,设,()f x ()g x ()h x ()h x t =,求出的解析式;2()(2)2()1()p t g x mh x m m m =++--∈R ()p t (3)若对任意都有成立,求实数m 的取值范围.[1,2]x ∈2()1p t m m ≥--【例题】某学校要建造一个面积为10000平方米的运动场。
如图,运动场是由一个矩形ABCD 和分别以AD 、BC 为直径的两个半圆组成。
跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮。
已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元(1)设半圆的半径(米),试建立跑道面积S 与r 的函数关系S(r )。
=OA r (2)由于条件限制[]30,40r ∈,问当r 取何值时,运动场造价最低?(精确到元)●某隧道长m ,最高限速为m/s 。
一个匀速进行的车队有10辆车,每辆车长为m ,相邻两车之a m 0v l 间距离m 与车速m/s 的平方成正比,比例系数为。
自第1辆车车头进隧道至第10辆车车尾离m v k 开隧道,所用时间为。
()t s (1)求出函数的解析式,并求出其定义域;()t f v =(2)求车队通过隧道时间的最小值,并求出取得最小值时的大小。
t t v回顾总结:1、通过Nike函数的图象,其性质都掌握了吗?2、求Nike函数的最值,步骤是____________________________________3、能转化为Nike函数的类型,具有的特点是____________________________________,求解最值所用的方法是____________________________________,用此种方法需要特别强调____________________________________4、含参数的Nike函数的最值,需要注意____________________________________5、含参数恒成立和有解问题,常用的方法是________________________________6、复合函数的单调性判断的方法是________________________________________。
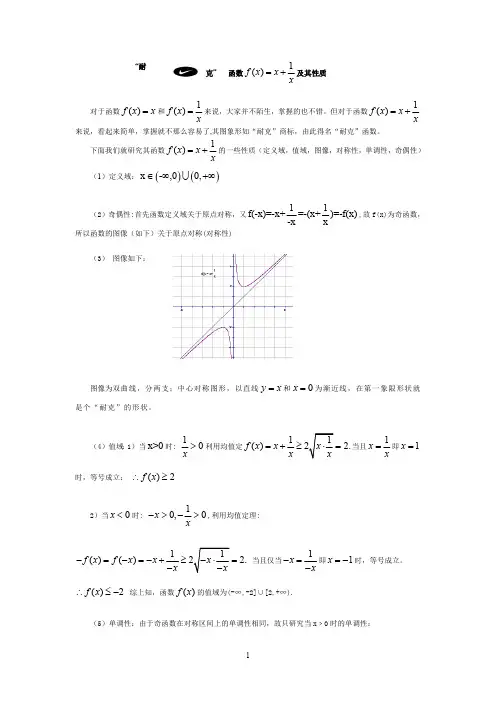
课题1:一次分式型函数、“耐克”函数 ● 教学目标:掌握一次分式型函数的定义、图像和性质,常见的分式型符合函数的性质和运算技巧; 掌握赖克函数的定义、图像和性质,常见与赖克函数相符合函数的性质和运算技巧;● 教学重点:图像和性质● 教学难点:性质的灵活运用● 教学过程一、一次分式型函数:1、定义:形如cx d b y x ax b a +⎛⎫=≠- ⎪+⎝⎭的函数,称为一次分式型函数; 2、图像:先分离常数:2d bc c a a y ba x a-=++,再由相应的反比例函数2''d bc a a y x -=平移而得到。
3(1c a ⎫≠⎬⎭(2,b a ⎛-∞- ⎝,b a ⎛⎫-∞- ⎪⎝⎭(3)对称性:关于',b c O a a ⎛⎫- ⎪⎝⎭成中心对称; (4)渐近线:直线b x a =-,c y a=是曲线的两条渐近线; 4、典型例题:例1、已知函数()1x f x x =+,求111(1)(2)()(3)()(4)()234f f f f f f f ++++++的值。
例2、已知函数()221x f x x =+,求()111(1)(2)(3)2010()()()232010f f f f f f f +++++++++L L 的值。
答案:120092。
二、“耐克”函数:1、两个重要不等式:重要不等式1:22,,2a b R a b ab ∈+≥(当且仅当a b =时取“=”号)重要不等式2:,,a b R a b +∈+≥(当且仅当a b =时取“=”号)图一:20d bc a a -> 图二:20d bc a a-<2、定义:形如()0b y ax x x =+≠的函数,称为“耐克”函数; 3、图像: ①当00a b >⎧⎨>⎩时,如图:① ②当00a b <⎧⎨<⎩时,如图:②③当00a b >⎧⎨<⎩时,如图:③ ④当00a b <⎧⎨>⎩时,如图:④4、性质:(1)定义域:{}0x x ≠; 值域:当00a b >⎧⎨>⎩,或00a b <⎧⎨<⎩时,值域为(),⎡-∞-+∞⎣U ; 当00a b <⎧⎨>⎩,或00a b >⎧⎨<⎩时,值域为(),-∞+∞。
专题:Nike 函数的图象和性质【复习要求】1、掌握耐克函数的图像与性质;2、会用耐克函数处理函数最值等问题;3、会解含参数的耐克函数的最值问题【知识板块】函数xx y 1+=你还记得吗?我们都研究了这个函数的哪些性质? (1) 定义域是____________ (2) 值域是____________ (3) 奇偶性是___________ (4) 单调性是___________ (5) 最值是_____________函数()0>+=a xax y 你还记得吗?我们都研究了这个函数的哪些性质?请画出图像再回答: (6) 定义域是___________(7) 值域是___________ (8) 奇偶性是___________ (9) 单调性是___________ (10) 最值是_____________ 思考:()0<+=a xax y 时,函数的以上性质有哪些变化?Oxyxy =xx y =+a【例题板块】【例题】求函数xx y 32+=的单调区间,并用函数单调性定义证明之。
● 函数xx y 94+=,]5,3[∈x 的最大、最小值?【例题】)21(12224)(2->+++=x x x x x f 的值域.● 已知0t >,求函数241t t y t-+=的最小值为.● 求)1(21)(2>++-=x x x x x f 的值域。
● 求函数4522++=x x y 的值域【例题】若,,3,x y R xy y +∈+=求x y +的最小值是;● 若,,2x y R x y xy +∈++=求x y +的最小值是;【例题】已知函数()2af x x x=+的定义域为(]0,2(a 为常数). (1)证明:当8a ≥时,函数()y f x =在定义域上是减函数;(2)求函数()y f x =在定义域上的最大值及最小值,并求出函数取最值时x 的值.● 已知]2,1[,3)(∈-+=x xbx x f (1) 2=b 时,求)(x f 的值域;(2) 2≥b 时,)(x f 的最大值为M ,最小值为m ,且满足:4≥-m M ,求b 的取值范围.● 已知函数xax y +=有如下性质:如果常数0>a ,那么该函数在],0(a 上是减函数,在),[+∞a 上是增函数.(1)如果函数)0(,3>+=x xx y m的值域是),6[+∞,求实数m 的值; (2)求函数)(x f =2x +2x a(0>a ) 在]2,1[∈x 上的最小值)(a g 的表达式.● 已知函数xax y +=有如下性质:如果常数a >0,那么该函数在(0,a ]上是减函数,在[a ,+∞)上是增函数.(1)如果函数y =x +x b2(x >0)的值域为[6,+∞),求b 的值;(2)研究函数y =2x +2x c (常数c >0)在定义域内的单调性,并说明理由;(3)对函数y =x +x a 和y =2x +2xa (常数a >0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数)(x F =n x x )1(2++nx x)1(2+(n是正整数)在区间[21,2]上的最大值和最小值(可利用你的研究结论).● (10奉贤一模)设()x m x x h +=,⎥⎦⎤⎢⎣⎡∈5,41x , 其中m 是不等于零的常数, (1)写出()x h 4的定义域; (2)求()x h 的单调递增区间;(3)已知函数()f x ([,])x a b ∈,定义:1()min{()|}f x f t a t x =≤≤([,])x a b ∈,2()max{()|}f x f t a t x =≤≤([,])x a b ∈.其中,min{()|}f x x D ∈表示函数()f x 在D 上的最小值,max{()|}f x x D ∈表示函数()f x 在D 上的最大值.例如:()cos f x x =,[0,]x π∈,则1()c o s ,[0,]f x xx π=∈ ,2()1,[0,]f x x π=∈ ,当1=m 时,设()()()()()2424x h x h x h x h x M -++=,不等式()()n x M x M t ≤-≤21【例题】若方程0122=+-ax x 在),3[+∞有解,求实数a 的取值范围.● 已知函数1()2x f x +=定义在R 上.(1)若存在x ,使得()()f x f x a +-=成立,求实数a 的取值范围;(2)若()f x 可以表示为一个偶函数()g x 与一个奇函数()h x 之和,设()h x t =,2()(2)2()1()p t g x mh x m m m =++--∈R ,求出()p t 的解析式;(3)若对任意[1,2]x ∈都有2()1p t m m ≥--成立,求实数m 的取值范围.【例题】某学校要建造一个面积为10000平方米的运动场。