幂函数的图像与性质(用).

指数函数的图像是一条向上开口的曲线，通常表示为y=a^x（a>0，a≠1）。

指数函数的性质有：
1.在y 轴上的截距为1。

2.对于不同的指数函数，它们的图像形状是相同的，只有位置不同。

如果改变指数函数的
指数，则会改变函数的斜率，即函数图像会发生平移。

3.对于相同的指数函数，如果改变函数的系数，则会改变函数的尺度，即函数图像会发生
伸缩。

对数函数的图像是一条向右开口的曲线，通常表示为y=loga(x)（a>0，a≠1）。

对数函数的性质有：
1.在y 轴上的截距为0。

2.对于不同的对数函数，它们的图像形状是相同的，只有位置不同。

如果改变对数函数的
底数，则会改变函数的斜率，即函数图像会发生平移。

3.对于相同的对数函数，如果改变函数的系数，则会改变函数的尺度，即函数图像会发生
伸缩。

幂函数的图像可以是一条向上开口的曲线，也可以是一条向右开口的曲线，通常表示为y=x^n（n为常数）。

幂函数的性质有：
1.当n>0 时，幂函数的图像是一条向上开口的曲线。

2.当n<0 时，幂函数的图像是一条向右开口的曲线。

3.当n=0 时，幂函数的图像是一条水平直线。

4.幂函数的图像在y 轴上的截距为1。

5.对于不同的幂函数，它们的图像形状是相同的，只有位置不同。

如果改变幂函数的指数，
则会改变函数的斜率，即函数图像会发生平移。

6.对于相同的幂函数，如果改变函数的系数，则会改变函数的尺度，即函数图像会发生伸
缩。

高一寒假数学讲义“幂函数的图像与性质（应用）”学生姓名授课日期教师姓名授课时长知识定位熟练掌握幂函数的概念，幂函数的图像及幂函数的性质，会解决幂函数的综合问题及应用问题。

知识梳理一、幂函数的定义一般地，形如y xα=（x∈R）的函数称为幂函数，其中x是自变量，α是常数.如11234,,y x y x y x-===等都是幂函数，幂函数与指数函数，对数函数一样，都是基本初等函数.幂函数的几个特点：（1）以自变量为底的幂；（3）指数为常数；（4）自变量前的系数为1；（5）幂前的系数也为1。

特别的：y=x0（x≠0）也是幂函数，因为00没有意义，所以要去掉点（0,1）；而y=1不是幂函数，是常数函数，定义域是x∈R。

二、幂函数的图像α取值范围不同，图像也不相同，α的正负：α＞0时，图象过原点和(1,1)，在第一象限的图象上升；α＜0时，图象不过原点，在第一象限的图象下降，反之也成立注意判断幂函数的定义域的方法可概括为（对指数）“先看正负，是负去零，再看奇偶，是偶非负”。

比如幂函数11234,,y x y x y x -===定义域分别为x ∈R ，x ∈R ，x ≠0。

三、 幂函数的性质（1）所有的幂函数在x ∈（0，+∞）都有定义,并且图象都通过点(1,1) （2）指数是偶数的幂函数是偶函数,指数是奇数的幂函数是奇函数 （3）α>0(1)图象都经过点（0，0）和（1，1） (2)图象在第一象限,函数是增函数. α<0(1)图象都经过点（1，1）； (2)图象在第一象限是减函数;(3)在第一象限内,图象向上与Y 轴无限接近,向右与X 轴无限地接近.四、 幂函数的运算（一）两个重要公式①⎪⎩⎪⎨⎧⎩⎨⎧<-≥==)0()0(||a a a a a a a n n ；②a a n n =)(（注意a 必须使n a 有意义）。

（二）有理数指数幂 （1）幂的有关概念①正数的正分数指数幂:(0,,1)m n m na a a m n N n *=>∈>、且; ②正数的负分数指数幂: 11(0,,1)mn m nmnaa m n N n a a-*==>∈>、且③0的正分数指数幂等于0,0的负分数指数幂没有意义.注：分数指数幂与根式可以互化，通常利用分数指数幂进行根式的运算。

幂函数图像及性质总结幂函数是高中数学中的一个重要概念，它是指形式为f(x)=ax^k的函数，其中a 为非零实数，k为实数。

幂函数在数学中具有广泛的应用，在图像的研究中，掌握幂函数的图像及其性质是非常重要的。

首先，我们来看幂函数的图像特点。

当k为正数时，幂函数的图像呈现出“增长”或“递减”的趋势。

当k>1时，曲线会明显上升，形成类似于指数函数的图像特征。

而当0<k<1时，曲线则会下降，但下降的速率逐渐减慢。

特别地，当k=1时，幂函数成为一次函数，即f(x)=ax，其图像为一条直线。

此外，当k为负数时，幂函数的图像则出现在第二、第四象限，并且具有对称轴。

接下来，我们来讨论幂函数的性质。

首先，我们来看函数的定义域和值域。

由于幂函数的底数a不能为零，函数的定义域为除以0的集合，即R-{0}。

而幂函数的值域则依赖于指数k的正负情况。

当k为正数时，函数的值域为正实数集(0,+∞)。

当k为负数时，函数的值域为(0, +∞)的实数集。

由于底数a的正负情况也会影响函数的关系，故在具体分析时需要考虑a的取值范围。

其次，我们来讨论幂函数的奇偶性。

当指数k为偶数时，幂函数f(x)=ax^k是一个偶函数，即满足f(x)=f(-x)。

这是因为对于任意x∈R，有(-x)^k=x^k，从而f(x)=ax^k=f(-x)。

相应地，当指数k为奇数时，幂函数f(x)=ax^k是一个奇函数，即满足f(x)=-f(-x)。

这是因为对于任意x∈R，有(-x)^k=-x^k，从而f(x)=ax^k=-ax^k=-f(-x)。

进一步地，我们来讨论幂函数的增减性和极值点。

当指数k为正数时，幂函数在定义域上是递增的。

当a>1时，函数的增长速度更快；当0<a<1时，函数的增长速度更慢。

而当指数k为负数时，幂函数在定义域上是递减的。

在图像上，幂函数具有一个最小值或最大值，该点称为极值点。

当k为偶数时，函数的极值点出现在定义域的最小值点，当k为奇数时，函数的极值点出现在定义域的最大值点。

幂函数知识点1. 幂函数定义幂函数是形如 \(y = x^n\) 的函数，其中 \(n\) 是实数。

当 \(n\) 为正整数时，幂函数的图像是一系列经过原点的点，且随着 \(n\) 的增加，曲线逐渐趋于平坦。

2. 幂函数的图像特征- 当 \(n > 1\) 时，幂函数在 \(x > 0\) 区域内单调递增。

- 当 \(0 < n < 1\) 时，幂函数在 \(x > 0\) 区域内单调递减。

- 当 \(n\) 为负整数时，幂函数在 \(x > 0\) 区域内表现为周期函数，周期为 \(4\pi\)。

- 当 \(n = 0\) 时，函数退化为常数函数 \(y = 1\)。

3. 幂函数的性质- 奇次幂函数是奇函数，即 \(y(-x) = -y(x)\)。

- 偶次幂函数是偶函数，即 \(y(-x) = y(x)\)。

- 幂函数的导数是 \(y' = n \cdot x^{n-1}\)。

- 幂函数的积分是 \(\int x^n dx = \frac{x^{n+1}}{n+1} + C\)，其中 \(C\) 是积分常数。

4. 幂函数的应用- 在物理学中，幂函数常用于描述物体的速度与加速度的关系。

- 在经济学中，幂函数可以用来模拟市场需求与价格的关系。

- 在工程学中，幂函数用于描述材料的强度与应力的关系。

5. 特殊幂函数- 指数函数 \(y = a^x\) 是幂函数的一种特殊形式，其中 \(a\) 是正实数且 \(a \neq 1\)。

- 对数函数 \(y = \log_a x\) 也是幂函数的一种特殊形式，其中\(a\) 是正实数且 \(a \neq 1\)。

6. 幂函数的运算法则- 幂的乘法：\(x^m \cdot x^n = x^{m+n}\)- 幂的除法：\(x^m / x^n = x^{m-n}\)- 幂的幂：\((x^m)^n = x^{m \cdot n}\)7. 幂函数的极限- 当 \(x \to 0\) 时，\(x^n\) 的极限取决于 \(n\) 的值。

幂函数与指数函数的性质幂函数和指数函数是数学中常见的两类函数，它们在数学和科学研究中有着重要的应用。

本文将探讨幂函数和指数函数的性质，包括定义、图像、增减性、奇偶性以及反函数等方面。

1. 幂函数的性质幂函数的一般形式为f(x) = x^n，其中n为正整数，是幂函数的指数。

幂函数的定义域为实数集，由于x^n中的n是正整数，所以幂函数的值域可以是正数、负数或零。

1.1. 幂函数的图像根据幂函数的指数n的奇偶性，幂函数的图像有不同的特点。

当n为偶数时，幂函数的图像相对于y轴对称，关于原点对称；而当n为奇数时，幂函数的图像关于原点对称。

1.2. 幂函数的增减性幂函数的增减性与指数n的值相关。

当指数n为正数时，幂函数在定义域上递增；当指数n为负数时，幂函数在定义域上递减。

值得注意的是，当指数n为偶数时，幂函数的绝对值增长速度比n为奇数时慢。

1.3. 幂函数的奇偶性当幂函数的指数n为偶数时，幂函数是偶函数；当指数n为奇数时，幂函数是奇函数。

这意味着幂函数的图像关于y轴对称或者关于原点对称。

1.4. 幂函数的反函数由于幂函数的定义域为实数集，而幂函数的指数并不一定能覆盖所有实数，所以幂函数的反函数并不一定存在。

当幂函数的指数n为倒数时，幂函数的反函数存在。

2. 指数函数的性质指数函数的一般形式为f(x) = a^x，其中a为常数，称为底数。

指数函数的定义域为实数集，底数a大于0且不等于1。

2.1. 指数函数的图像指数函数的图像与底数a有关。

当底数a大于1时，指数函数在整个定义域上递增；当底数a介于0和1之间时，指数函数在整个定义域上递减。

指数函数的图像经过点(0, 1)，即当x等于0时，指数函数的值为1。

2.2. 指数函数的增减性指数函数的增减性取决于底数a的值。

当底数a大于1时，指数函数在整个定义域上递增；当底数a介于0和1之间时，指数函数在整个定义域上递减。

2.3. 指数函数的奇偶性指数函数一般情况下不具有奇偶性，即指数函数的图像不关于y轴对称也不关于原点对称。

高中幂函数图像及性质
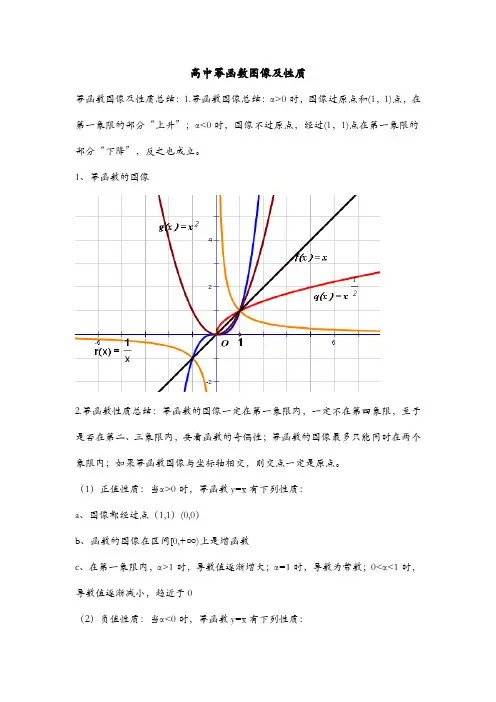
幂函数图像及性质总结：1.幂函数图像总结：α>0时，图像过原点和(1，1)点，在第一象限的部分“上升”；α<0时，图像不过原点，经过(1，1)点在第一象限的部分“下降”，反之也成立。

1、幂函数的图像
2.幂函数性质总结：幂函数的图像一定在第一象限内，一定不在第四象限，至于是否在第二、三象限内，要看函数的奇偶性；幂函数的图像最多只能同时在两个象限内；如果幂函数图像与坐标轴相交，则交点一定是原点。

（1）正值性质：当α>0时，幂函数y=x有下列性质：
a、图像都经过点（1,1）(0,0）
b、函数的图像在区间[0,+∞)上是增函数
c、在第一象限内，α>1时，导数值逐渐增大；α=1时，导数为常数；0<α<1时，导数值逐渐减小，趋近于0
（2）负值性质：当α<0时，幂函数y=x有下列性质：
a、图像都通过点（1,1）
b、图像在区间（0，+∞）上是减函数；（内容补充：若为X易得到其为偶函数。

利用对称性，对称轴是y轴，可得其图像在区间（-∞，0）上单调递增。

其余偶函数亦是如此）
c、在第一象限内，有两条渐近线（即坐标轴），自变量趋近0，函数值趋近+∞，自变量趋近+∞，函数值趋近0。

幂函数的性质与图象上海大学附属中学 钱寒静【教学材料】高中一年级第一学期数学4.1《幂函数的性质与图像》【教材分析】幂函数、指、对函数是最基本、最常用的函数模型，是学习其它函数的基础。

学生在初中已经学过了正比例、反比例、一次和二次函数，学过指数和幂的知识，本节课是在初中知识的基础上对形如）为常数（Q ，k k x y k∈= 的函数进行系统、全面的探究，这既有利于学生对函数概念的理解，又对今后学习其它函数提供了方法，从而提高学生的数学应用能力。

【学情分析】 学生在初中已经接触过函数，学习过有关幂的运算性质，并具有一定的列表、画图的能力，授课的班级为上海市示范性高中的学生，他们的数学基础扎实。

【教学目标】知识与技能：1、 知道幂函数的概念，理解幂函数当k>0时在第一象限内的图象特征；2、 类比让学生发现当k<0时，幂函数在第一象限内的图象特征；3、掌握幂函数当k 变化时的图象特征；过程能力与方法：在教学中充分发挥学生的主体作用，让他们经历幂函数性质发现的全过程，体会数形结合的数学思想，体验从特殊到一般的研究方法，学会观察反思，最终自己得到幂函数的所有性质。

情感、态度与价值观：让学生认识到幂函数图象的奇特魅力，体会数学的对称美与和谐美，增强学生科学严谨的学习态度，最终深刻理解到量变引起质变的哲学道理。

【重点难点】重点：幂函数的概念和幂函数在第一象限内的图象性质。

难点：幂函数性质的总结。

【教学方法】采用“引导、探究、再创”的教学模式，即引导学生观察特例，提炼规律，化抽象为具体，探究其性质，再化具体规律到一般规律。

【教学手段】多媒体辅助教学。

【教学过程】一、 引入：以教材的编排为切入点，说明我们学习函数的定义域、值域、奇偶性、单调性等一系列性质都是为了研究具体的函数，今天我们就来研究一类新的函数：幂函数。

二、 幂函数的定义： 形如）为常数（Q ，k k x y k∈= 的函数叫做幂函数。

例1：判断下列函数是否是幂函数： x y x y x y x y -==+== )4( )3( 1 )2( 4 )1(322三、 研究幂函数的图象：1、 在幂函数作图器中任意做出几个幂函数的图象。

幂函数和根函数的象和性质幂函数是指数函数的特殊形式，而根函数则是幂函数的逆运算。

它们是数学中一个重要的函数类型，具有一些特殊的性质和象。

本文将就幂函数和根函数的象和性质进行详细的讲解。

一、幂函数的象和性质幂函数的一般形式为 f(x) = x^a，其中 a 是实数。

幂函数的定义域可以是整个实数集，而值域则取决于指数 a 的奇偶性。

1. 当 a 是正整数时，幂函数的值域为正实数集。

例如，f(x) = x^2 是一个以原点为顶点的抛物线，它的象是大于等于零的所有实数。

2. 当 a 是负整数时，幂函数的值域为正实数集的倒数。

例如，f(x) = x^(-1) 是一个双曲线，它的象是所有不等于零的实数。

3. 当 a 是零时，幂函数变为常数函数 f(x) = 1，其象为常数 1。

4. 当 a 是分数时，幂函数的值域可以是整个实数集。

例如，f(x) = x^(1/2) 是一个以原点为顶点的开口向上的抛物线，它的象是大于等于零的所有实数。

幂函数具有以下性质：1. 幂函数是单调递增的，当 a 是正数时，函数的增长速度更快；当a 是负数时，函数的增长速度越来越慢。

2. 幂函数在 x = 0 处一般是不连续的，当 a 是正数时，零的左侧没有定义；当 a 是负数时，零的右侧没有定义。

3. 幂函数的图像关于 y 轴对称，即 f(x) = f(-x)。

二、根函数的象和性质根函数的一般形式为f(x) = √x，其中 x 是非负实数。

根函数的定义域是非负实数的集合，值域则取决于根指数的奇偶性。

1. 当根指数是奇数时，根函数的象是非负实数集。

例如，f(x) = √x 是一个以原点为顶点的开口向上的抛物线，它的象是大于等于零的所有实数。

2. 当根指数是偶数时，根函数的象是非负实数集的零点。

例如，f(x) = √(x^2) 是一条以原点为对称轴的折线，它的象是大于等于零的所有实数。

根函数的主要性质包括：1. 根函数是单调递增的，且具有一次连续性。

《幂函数的性质与图像》教学案例一、【教学内容分析】幂函数是在学生系统学习了函数概念与函数性质之后，全面掌握有理指数幂和根式的基础上来研究的一种特殊函数，从教材的整体安排看，学习幂函数是为了让学生进一步获得比较系统的函数知识及研究函数的方法，为今后学习其他函数打下良好的基础。

对幂函数进行系统的理论研究，在研究过程中得出相应的结论固然重要，但更为重要的是，要让学生了解系统研究一类函数的方法。

这节课要特别让学生去体会研究的方法，以便能将该方法迁移到对其他函数的研究中。

二、【学情分析】从学生思维特点来和认知结构看，学生在初中学过了一次函数、二次函数、反比例函数，学生对抽象的幂函数及其图像有些感性认识，缺乏在理解理性的基础上来运用幂函数的性质。

但只要从实际问题出发，使他们从感性认识提高到理性认识，多运用数形结合的方法解决问题，提高学生分析问题、解决问题的能力。

三、【教学目标】1、理解幂函数的意义，能通过几个有代表性的幂函数图象的求作、观察、分析、归纳体会幂函数图象变化规律及幂函数的性质，体会从特殊到一般的研究问题的数学方法并能进行简单应用。

2、增强自我抽象概括和识图能力，运用性质解决问题时，进一步体会数形结合思想。

形成竞赛机制，使学生认识到传统和现代技术在数学认知过程中的作用，从而激发学生的学习欲望，提高学生的学习能力，养成积极主动，勇于探索，不断创新的学习习惯和品质。

四、【教学重点难点】【重点】幂函数的概念；幂函数的图像与性质。

【难点】画具体幂函数的图象并由图象概括其性质，体会图象的变化规律；幂函数的性质的应用。

五、【教法学法分析】教和学是不可分的。

通过课前学案的创设疑问，学生对问题的共同探究，通过课堂教师的点拨，启发学生主动观察、思考、动手操作、合作和探究来达到对知识的发现和接受。

逐步解决问题。

采用引导发现式的教学方法，充分利用多媒体辅助教学。

具体安排如下：1、通过小组利用学案探究完成【探究一】及【探究二】2、通过课堂交流研讨展示成果，并及时地发现自己的不足，并能及时修正。