实验三 二阶系统频率响应

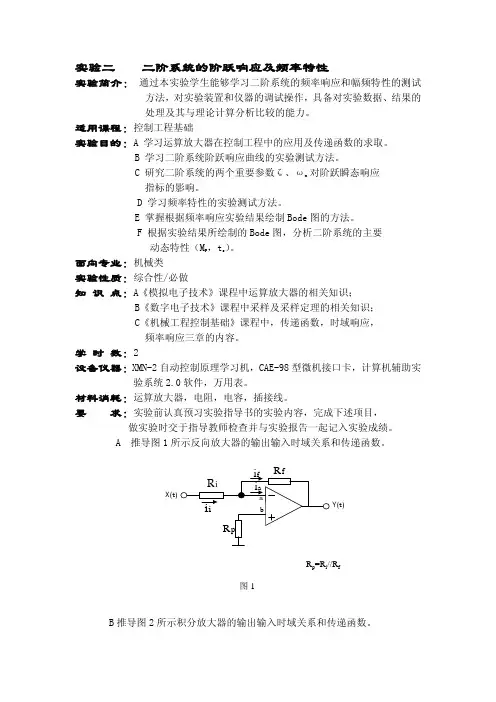
实验二二阶系统的阶跃响应及频率特性实验简介：通过本实验学生能够学习二阶系统的频率响应和幅频特性的测试方法，对实验装置和仪器的调试操作，具备对实验数据、结果的处理及其与理论计算分析比较的能力。

适用课程：控制工程基础实验目的：A 学习运算放大器在控制工程中的应用及传递函数的求取。

B 学习二阶系统阶跃响应曲线的实验测试方法。

C 研究二阶系统的两个重要参数ζ、ωn对阶跃瞬态响应指标的影响。

D 学习频率特性的实验测试方法。

E 掌握根据频率响应实验结果绘制Bode图的方法。

F 根据实验结果所绘制的Bode图，分析二阶系统的主要动态特性（MP ，ts）。

面向专业：机械类实验性质：综合性/必做知 识 点：A《模拟电子技术》课程中运算放大器的相关知识；B《数字电子技术》课程中采样及采样定理的相关知识；C《机械工程控制基础》课程中，传递函数，时域响应， 频率响应三章的内容。

学 时 数：2设备仪器：XMN-2自动控制原理学习机，CAE-98型微机接口卡，计算机辅助实验系统2.0软件，万用表。

材料消耗：运算放大器，电阻，电容，插接线。

要 求：实验前认真预习实验指导书的实验内容，完成下述项目， 做实验时交于指导教师检查并与实验报告一起记入实验成绩。

B推导图2所示积分放大器的输出输入时域关系和传递函数。

C 推导图3所示加法和积分放大器的输出输入时域关系（两输入单输出）和S<1>.写出op1,op2,op9,0p6对应的微分方程组（4个方程）。

<2>.画出系统方框图。

<3>.用方框图化简或方程组联立消元的方法求取实验电路所示系统的传递函数，写出求解过程。

和ζ。

<4>.求取该系统的ωn实验地点：教一楼327室实验照片：实验装置及仪器。

实验三 二阶系统频率响应一、实验目的（1）学习系统频率特性响应的实验测试方法。

（2）了解二阶闭环系统中的对数幅频特性和相频特性的计算。

（3）掌握根据频率响应实验结果绘制波特图的方法。

（4）掌握欠阻尼二阶闭环系统中的自然频率、阻尼比对谐振频率、谐振峰值和带宽的影响及对应的计算。

二、实验设备（1）XMN-2型学习机；（2）CAE-USE 辅助实验系统 （3）万用表 （4）计算机 三、实验内容本实验用于观察和分析二阶系统瞬态响应的稳定性。

二阶闭环系统模拟电路如图3-1所示，它由两个积分环节（OP1和OP2）及其反馈回路构成。

图3-1 二阶闭环系统模拟电路图OP1和OP2为两个积分环节，传递函数为sT s G i 1)(-=（时间常数RC T i =）。

二阶闭环系统等效结构图如图3-2所示。

图3-2 二阶闭环系统等效结构图该二阶系统的自然振荡角频率为RC T n 11==ω，阻尼为ifR R K 22==ζ。

四、实验步骤（1）调整Rf=40K ，使K=0.4（即ζ=0.2）；取R=1M ，C=1μ，使T=1秒（ωn=1/1）。

（2）输入信号位)sin(t X ω=，改变角频率使ω分别为0.2,0.6,0.8,0.9,1.0,1.2,1.6,2.0,3.0rad/s 。

稳态时，记录下输出响应)sin(φω+=t Y y 五、数据采集及处理输出信号幅值Y输出信号初相φL(ω)φ(ω)ω(rad/s)T0.2 0.6 0.8 0.9 1.0 1.21.62.03.0六、实验报告1、绘制系统结构图，并求出系统传递函数，写出其频率特性表达式。

2、用坐标纸画出二阶闭环系统的对数幅频、相频曲线（波特图）。

3、其波特图上分别标示出谐振峰值（Mr）、谐振频率（ωr）和带宽频率（ωb）。

4、观察和分析曲线中的谐振频率（ωr）、谐振峰值（Mr）和带宽（ωb），并与理论计算值作对比。

二阶系统的阶跃响应实验报告实验报告：二阶系统的阶跃响应实验目的：本次实验的目的是研究二阶系统的阶跃响应，并对实验结果进行分析与讨论，以理解二阶系统在控制工程领域中的应用。

实验原理：二阶系统是指具有二阶特性的系统，即在系统受到激励信号后，系统的响应随时间的变化呈现出一定的规律。

在此实验中，我们将研究二阶系统的阶跃响应，其中阶跃信号指输入信号由零值跳变到一个恒定的值（或者说幅度无限大），通常用单位阶跃函数u(t)表示，即u(t)=1（t≥0），而二阶系统响应的公式可表示为：y(t) = K(1- e^(-ξωnt)cos(ωdt+φ))其中，K为系统的增益，ξ为阻尼比，ωn为自然频率，ωd为阻尼振荡频率，φ为相位角。

实验步骤：1. 确定实验装置的参数，并将之记录下来，包括：二阶系统的增益K、阻尼比ξ、自然频率ωn，以及阶跃信号的幅值u0等。

2. 将二阶系统的输入信号设置为阶跃信号u(t)，并将输出信号y(t)记录下来，同时进行数据采集和记录。

3. 根据数据得出实验结果，并利用软件对实验数据进行处理和分析，包括波形比较、响应曲线分析和幅值与相位移测量等。

实验结果：在此次实验中，我们得到了如下的实验参数：增益K = 1.5V阻尼比ξ = 0.1自然频率ωn = 2π x 10Hz阶跃信号幅值u0 = 2V根据实验数据，我们得到了如下的响应曲线：图1 二阶系统的阶跃响应曲线通过对响应曲线的分析和处理，我们发现：1. 二阶系统的阶跃响应具有一定的超调和振荡特性，表明系统的稳定性较差，需要进行进一步的优化和调整。

2. 阻尼比ξ的大小与系统的响应有着密切的关系，通常应根据系统的具体情况进行合理的选择和调整，以达到最佳的控制效果。

3. 自然频率ωn的大小与系统的响应速度有关，通常应根据实际控制要求进行选择和调整，以达到最佳的控制效果。

结论：本次实验研究了二阶系统的阶跃响应，并对实验结果进行分析和讨论。

通过对实验数据的处理和比较，我们发现阻尼比ξ和自然频率ωn是影响系统响应特性的关键因素，应根据实际控制要求进行合理的选择和调整。

二阶系统的阶跃响应实验报告实验名称：二阶系统的阶跃响应实验报告实验目的：1. 了解二阶系统的阶跃响应特性，掌握二阶系统的调节方法。

2. 学习使用计算机实验仿真软件，分析控制系统的特性和设计计算机系统的参数。

3. 进一步了解数字控制的基本原理和实现方法。

实验原理：二阶系统指的是包含两个振动元件的控制系统，例如质量弹簧阻尼系统、旋转系统等。

通过向系统输入一个单位阶跃信号，可以使系统达到稳态。

在达到稳态后，可以观察到系统的响应特性，例如响应时间、超调量等。

二阶系统的阶跃响应有三种情况，分别为欠阻尼、临界阻尼和过阻尼。

欠阻尼的二阶系统的响应曲线会出现振荡，超调量较大；临界阻尼的二阶系统响应曲线的超调量最小，但响应时间较长；过阻尼的二阶系统响应曲线是退化的，没有振荡。

在实验中，我们使用计算机模拟二阶系统，并通过输入一个单位阶跃信号，观察系统的响应特性。

具体操作步骤如下：1. 在仿真软件中建立一个二阶系统，可以让仿真软件自动生成一个简单的二阶系统。

2. 将系统设置为单位阶跃信号输入，运行仿真，观察系统的响应特性。

3. 记录系统的超调量、响应时间以及稳态误差等参数。

4. 在仿真软件中改变系统的参数，例如增加阻尼系数，观察系统的响应变化。

实验器材：1. 计算机2. 仿真软件实验步骤：1. 打开计算机，并运行仿真软件。

2. 在仿真软件中建立一个二阶系统，并设置其为单位阶跃信号输入。

3. 运行仿真，并记录系统的响应特性，包括超调量、响应时间以及稳态误差等参数。

4. 在仿真软件中改变系统的参数，例如增加阻尼系数，观察系统的响应变化，并记录变化后的参数。

5. 分析实验结果，并总结出二阶系统的阶跃响应特性。

实验结果：在实验中，我们使用了仿真软件模拟了一个简单的二阶系统，并进行了阶跃响应实验。

通过实验，我们观察到了系统的响应特性，并记录了系统的超调量、响应时间以及稳态误差等参数。

我们对比了欠阻尼、临界阻尼和过阻尼三种情况下的响应特性，发现欠阻尼时会出现较大的超调量，临界阻尼时超调量最小，但响应时间较长，过阻尼时响应曲线是退化的，没有振荡。

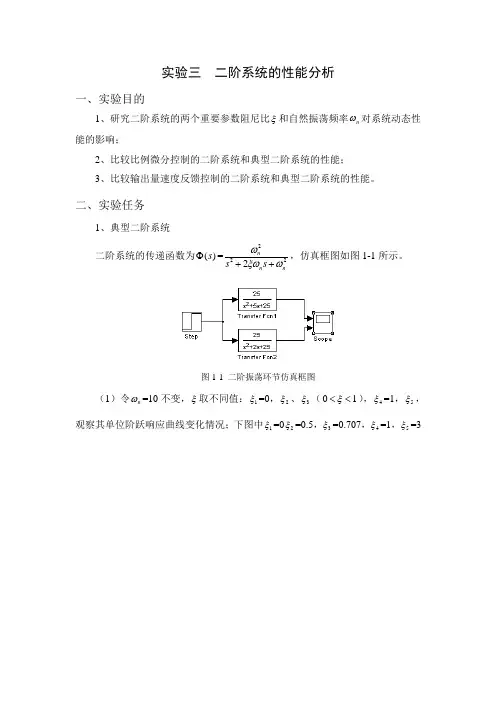
实验三 二阶系统的性能分析一、实验目的1、研究二阶系统的两个重要参数阻尼比ξ和自然振荡频率n ω对系统动态性能的影响；2、比较比例微分控制的二阶系统和典型二阶系统的性能；3、比较输出量速度反馈控制的二阶系统和典型二阶系统的性能。

二、实验任务1、典型二阶系统二阶系统的传递函数为()s Φ=2222nn ns s ωξωω++，仿真框图如图1-1所示。

图1-1 二阶振荡环节仿真框图（1）令n ω=10不变，ξ取不同值：1ξ=0，2ξ、3ξ（01ξ<<），4ξ=1，5ξ，观察其单位阶跃响应曲线变化情况；下图中1ξ=02ξ=0.5，3ξ=0.707，4ξ=1，5ξ=3（2）令ξ=0不变，ω取不同值，观察其单位阶跃响应曲线变化情况；（3）令ξ=0.2不变，ω取不同值，观察其单位阶跃响应曲线变化情况，并计算超调量%和t；s（4）令n ω=10不变，ξ取不同值（01ξ<<），观察其单位阶跃响应曲线变化情况，并计算超调量%σ和s t 。

2、比例微分控制的二阶系统比例微分控制的二阶系统的结构图如图2-1。

图2-1 比例微分控制的二阶系统的结构图系统中加入比例微分控制，使系统阻尼比增加，并增加一个闭环零点，可以通过仿真比较典型二阶系统和比例微分控制的二阶系统的单位阶跃响应的性能指标。

上图所示的控制系统，令225(2)(2)nns s s sωξω=++，0.1dT=，其中5,0.2nωξ==，从Simulink图形库浏览器中拖曳Step（阶跃输入）、Sum（求和模块）、Pole-Zero （零极点）模块、Scope（示波器）模块到仿真操作画面，连接成仿真框图如图2-2所示。

图中Pole-Zero（零极点）模块建立()G s。

图2-2 典型二阶系统和比例微分控制的二阶系统比较仿真框图3、输出量速度反馈的二阶系统输出量速度反馈的二阶系统的结构图如图2-3。

图2-3 输出量速度反馈的二阶系统的结构图系统中加入输出量的速度反馈控制，使系统阻尼比增加，可以通过仿真比较典型二阶系统和输出量速度反馈控制的二阶系统的单位阶跃响应的性能指标。

自控实验—二三阶系统动态分析在自控实验中，二、三阶系统动态分析是非常重要的一部分。

通过对系统的动态性能进行分析，可以评估系统的稳定性、响应速度和稳态误差等方面的性能。

本次实验将使用PID控制器对二、三阶系统进行实时控制，并通过实验数据对系统进行动态分析。

首先，我们先了解什么是二、三阶系统。

在控制系统中，系统的阶数表示系统传递函数的阶数，也可以理解为系统动态特性的复杂程度。

二阶系统由两个极点和一个零点组成，三阶系统由三个极点和一个零点组成。

二、三阶系统的动态响应特性与极点位置有关，不同的极点位置对系统的稳定性、响应速度和稳态误差等性能有着不同的影响。

在实验中，我们将使用PID控制器对二、三阶系统进行控制。

PID控制器是一种经典的比例-积分-微分控制器，可以根据误差信号进行调节，通过调整比例系数、积分时间和微分时间来控制系统的响应特性。

实验中，我们将根据二、三阶系统的实时数据进行PID参数调整，以达到控制系统的稳定和快速响应的目的。

在进行实验前，我们首先需要对二、三阶系统进行建模。

二、三阶系统的传递函数通常表示为：二阶系统：G(s) = K / (s^2 + 2ξω_ns + ω_n^2)三阶系统：G(s) = K / (s^3 + 3ξω_ns^2 + 3ω_n^2s + ω_n^3)其中，K表示系统的增益，ξ表示系统的阻尼比，ω_n表示系统的自然频率。

通过实验数据的统计和分析，我们可以估计出系统的K、ξ和ω_n的值，并据此进行PID参数的调整。

接下来，我们进行实验。

我们首先将PID控制器的参数设为初始值，然后对系统进行实时控制，并记录系统输出的数据。

通过对这些数据进行分析，我们可以得到系统的稳态误差、响应时间和超调量等性能指标。

对于二阶系统，我们将分析以下几个方面的性能：1.稳态误差：通过比较实际输出值与目标值之间的差异，可以得到系统的稳态误差。

常见的稳态误差有零稳态误差、常数稳态误差和比例稳态误差等。

二阶系统的频率响应一、实验目的1．掌握典型二阶系统频率响应的实验测试方法； 2．根据实验数据绘制典型二阶系统的Bode 图；3．根据绘制的Bode 图，分析二阶系统参数ζ和ωn 对系统频率特性的影响。

二、实验设备1．控制系统综合实验台（XMN-2型） 1台 2．慢扫描双踪示波器 1台 3．超低频信号发生器 1台 4．数字万用表 1块 5．连接导线 若干 三、实验内容与方法图3-1是典型二阶系统的方框图()22n n n n 11ωωωωω1212ωωωωG j j j j ζζ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫++-⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎝⎭⎝⎭⎣⎦系统的频率响应为：＝＝＋图3-2是典型二阶系统的模拟电路图图3-1图3-2n ωf iR R RC 1图中：＝21＝实验步骤1．在控制系统综合实验台上，用运算放大器、电阻和电容组建典型的二阶系统，并将超低频信号发生器输出的正弦波作为二阶系统的输入信号，信号峰值为1伏；2．选择R 、C 、R i 和R f 的值，保持系统的ωn =1和ζ＝0.2不变，改变输入信号的频率，使对应的角频率ω分别等于0、0.2、0.4、0.6、0.8、0.9、1.0、2.0、4.0、6.0、8.0、10，20、40、60、80、100rad/s ，并同时记录稳态时系统正弦输入信号和正弦输出信号的电压有效值和相位差；3．保持系统的ωn =1和ζ＝0.7不变，重复步骤24．根据实验数据分别绘制两种情况下二阶系统的的Bode 图，并分析阻尼比ζ对系统的谐振峰值、谐振频率、稳定性和稳定裕量的影响。

5．选择R 、C 、R i 和R f 的值，保持系统的ζ＝0.7和ωn =0.1不变，重复步骤26．选择R 、C 、R i 和R f 的值，保持系统的ζ＝0.7和ωn =10不变，重复步骤2 四、实验报告要求实验报告应包括硬件接线图、实验数据表、不同ζ和ωn 值条件下的Bode 图、性能指标对比和分析结论。

频率响应测试37030602 王世婷一、 实验目的1. 掌握频率特性的测试原理及方法；2. 学习根据所测定出的系统的频率特性，确定系统传递函数的方法。

二、 实验内容1. 测定给定环节的频率特性。

2. 测定环节构成系统的幅频特性及相频特性，测定输入与输出信号幅值12A A 及，然后计算其比值21/A A ，计算相位差角ψ。

三、 实验原理若正弦输入信号为1sin()i u A t ω=，则当输出达到稳态时，其输出信号为2sin()o u A t ωψ=+。

改变输入信号频率2f ωπ=值，便可测得二组12/A A 和ψ随f(或ω)变化的数值，此规律即为系统的幅频特性和相频特性。

1. 幅频特性即测量输入与输出信号幅值12A A 及，然后计算其比值21/A A 。

2. 实验采用“李沙育图形”法进行相频特性的测试。

原理如下：设有两个正弦信号：()sin()m X w t X w t = ()s i n (m Y w t Y wt ψ=+ 若以X （t ）为横轴，Y （t ）为纵轴，而以ω作为参变量，则随着w t 的变化，X （t ）和Y （t ）所确定的点的轨迹，将在X-Y 平面上描绘出一条封闭的曲线。

此即为物理学上的李沙育图形，如图所示。

图1-1不同的正弦波（同频率、不同相位、不同幅度）合成的李萨如图形不同，椭圆长轴方向也分为左倾和右倾，如下图所示：图1-2 左倾 图1-3右倾 本文以“/”表示右倾，“\”表示左倾。

3. 相位差角ψ的求法：对于()s i n ()m X w t X w t =及()sin()m Y w t Y w t ψ=+，当0w t =时，有(0)0X =，(0)sin()m Y Y ψ=，即a rc s i n ((0)/)mY Y ψ=，显然，仅当0/2ψπ≤≤时，上式成立。

此实验中，121,m m X A V Y A ===，当椭圆右倾时，02πψ-≤≤，arcsin((0)/)m Y Y ψ=-；当椭圆左倾时，2ππψ-≤≤-，arcsin((0)/)m Y Y ψπ=-+。

实验二二阶系统阶跃响应一、实验目的1．研究二阶系统的特征参数，阻尼比ζ和无阻尼自然频率ωn对系统动态性能的影响。

定量分析ζ和ωn与最大超调量Mp和调节时间t S之间的关系。

2．进一步学习实验系统的使用方法3．学会根据系统阶跃响应曲线确定传递函数。

二、实验仪器1．EL-AT-III型自动控制系统实验箱一台2．计算机一台三、实验原理1．模拟实验的基本原理：控制系统模拟实验采用复合网络法来模拟各种典型环节，即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节，然后按照给定系统的结构图将这些模拟环节连接起来，便得到了相应的模拟系统。

再将输入信号加到模拟系统的输入端，并利用计算机等测量仪器，测量系统的输出，便可得到系统的动态响应曲线及性能指标。

若改变系统的参数，还可进一步分析研究参数对系统性能的影响。

2. 域性能指标的测量方法：超调量Ó%：1）启动计算机，在桌面双击图标 [自动控制实验系统] 运行软件。

2) 检查USB线是否连接好，在实验项目下拉框中选中实验，点击按钮，出现参数设置对话框设置好参数，按确定按钮，此时如无警告对话框出现表示通信正常，如出现警告表示通信不正常，找出原因使通信正常后才可以继续进行实验。

3)连接被测量典型环节的模拟电路。

电路的输入U1接A/D、D/A卡的DA1输出，电路的输出U2接A/D、D/A卡的AD1输入，将两个积分电容连在模拟开关上。

检查无误后接通电源。

4)在实验项目的下拉列表中选择实验二[二阶系统阶跃响应] 。

5)鼠标单击按钮，弹出实验课题参数设置对话框。

在参数设置对话框中设置相应的实验参数后鼠标单击确认等待屏幕的显示区显示实验结果6)利用软件上的游标测量响应曲线上的最大值和稳态值，代入下式算出超调量：Y MAX - Y∞Ó%=——————×100%Y∞T P与T P：利用软件的游标测量水平方向上从零到达最大值与从零到达95%稳态值所需的时间值，便可得到T P与T P。

二阶系统的特性测量实验报告介绍本报告旨在介绍二阶系统的特性测量实验所需的步骤和过程。

二阶系统通常用于描述许多物理现象，如振动、波动和控制系统。

在本实验中，我们将探讨二阶系统的频率响应和阶跃响应。

我们还将测量系统的反馈增益和阻尼比，并验证系统是否稳定。

实验步骤1.实验装置在本实验中，我们将使用以下装置：（1）示波器（2）信号发生器（3）二阶系统模块（4）电缆（5）电源2.频率响应（1）将示波器和信号发生器连接到二阶系统模块。

（2）将信号发生器设置为正弦波，并将频率设置为低于系统的共振频率。

（3）使用示波器测量系统的输入和输出信号，并计算系统的增益和相位差。

（4）逐渐增加信号发生器的频率并再次测量增益和相位差。

记录数据。

（5）绘制增益与频率的图表，以确定系统的特性。

3.阶跃响应（1）将信号发生器连接到二阶系统模块，将输出连接到示波器。

（2）将信号发生器的设置改为阶跃波形，并逐渐增加幅度。

（3）测量系统的阶跃响应，并计算系统的上升时间、峰值时间、峰值值和稳定时间。

4.反馈增益和阻尼比（1）将信号发生器连接到二阶系统模块的输入。

（2）将示波器连接到系统模块的输出，并记录系统的输出信号的振幅。

（3）逐渐增加系统的反馈增益，并记录输出信号的振幅的变化。

（4）使用数据计算系统的阻尼比。

5.验证系统稳定性（1）将系统模块的输入和输出连接到示波器。

（2）使系统运行并观察输出信号。

（3）传递函数的特定零点和极点会决定系统是否稳定。

如果系统有零点或极点在右半平面则不稳定，否则系统是稳定的。

结论二阶系统主要是用于描述许多物理现象的，包括振动、波动和控制系统。

在本实验中，我们探讨了二阶系统的频率响应和阶跃响应。

我们还测量了系统的反馈增益和阻尼比，并验证了系统是否稳定。

这些实验有助于我们更好地了解二阶系统的特性和如何分析和控制它们。

实验三——二阶系统的时域响应及性能分析实验三主要研究了二阶系统的时域响应及其性能分析，通过实验得到不同二阶系统的单位阶跃响应和单位脉冲响应，并对其进行分析和性能评估。

首先，实验中使用的二阶系统是由两个一阶系统串联而成，可以通过两个一阶系统的参数来确定二阶系统的性能。

实验中设置了不同的参数组合来得到不同的二阶系统，并测量了这些系统的单位阶跃响应和单位脉冲响应。

实验中，单位阶跃响应是通过给系统输入一个单位阶跃信号，观察系统的输出得到的。

单位脉冲响应是通过给系统输入一个单位脉冲信号，观察系统的输出得到的。

通过测量这两个响应，可以了解二阶系统在时域的性能。

对于单位阶跃响应，实验中测量了系统的超调量、调整时间和稳态误差。

超调量是指单位阶跃响应中最高峰值与稳态值之差与稳态值的比值，可用来评估系统的动态性能。

调整时间是指从单位阶跃信号开始输入到响应达到其稳态值所需要的时间，反映了系统调整过程的快慢。

稳态误差是指系统最终的输出值与期望值之差，用来评估系统的稳态准确性。

对于单位脉冲响应，实验中测量了系统的峰值和时间常数，用来评估系统的动态特性。

峰值是指单位脉冲响应中的最高值，与系统的阻尼比有关。

时间常数是指单位脉冲响应中曲线从0到达其最大值所需要的时间，与系统的阻尼比和自然频率有关。

通过实验数据的测量和分析，可以得到不同参数组合下的二阶系统的性能指标，进而对系统进行评估。

如果超调量小、调整时间短、稳态误差小，表示系统的动态特性优秀，能够快速、准确地响应输入信号；如果峰值小、时间常数短，表示系统的动态特性好，有较快的响应速度和较小的振荡现象。

综上所述，实验三通过对二阶系统的时域响应进行测量和分析，并对性能指标进行评估，可以得到不同二阶系统的动态特性和稳态准确性信息。

这些信息对于系统设计和参数调整具有重要的参考价值。

通过实验的学习，可以更深入地理解掌握二阶系统的性能分析方法，为系统控制和优化提供理论和实践基础。

一典型系统的时域响应和稳定性分析一、实验目的1．研究二阶系统的特征参量（ξ、ωn）对过渡过程的影响。

2．研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。

3．熟悉Routh判据，用Routh判据对三阶系统进行稳定性分析。

二、实验原理及内容1．典型的二阶系统稳定性分析(1) 结构框图：见图1图1(2) 对应的模拟电路图图2(3) 理论分析导出系统开环传递函数，开环增益。

系统开环传递函数为：G(S) = =开环增益为：K=K1/K0(4) 实验内容先算出临界阻尼、欠阻尼、过阻尼时电阻R的理论值，再将理论值应用于模拟电路中，观察二阶系统的动态性能及稳定性，应与理论分析基本吻合。

在此实验中(图2)，s 1T 0=， s T 2.01=，R200K 1= R200K =⇒系统闭环传递函数为：KS S KS S S W n n n 5552)(2222++=++=ωζωω 其中自然振荡角频率：R1010T K 1n ==ω；阻尼比：40R1025n =ω=ζ2．典型的三阶系统稳定性分析 (1) 结构框图图3(2) 模拟电路图图4(3) 理论分析系统的开环传函为:)1S 5.0)(1S 1.0(S R 500)S (H )S (G ++=(其中R 500K =)，系统的特征方程为:0K 20S 20S 12S 0)S (H )S (G 123=+++⇒=+。

(4) 实验内容从Routh 判据出发，为了保证系统稳定，K 和R 如何取值，可使系统稳定，系统临界稳定，系统不稳定三、 实验现象分析1．典型二阶系统瞬态性能指标表1其中21e Mp ζ-ζπ-=，2np 1t ζ-ωπ=，n s 4t ζω=，21p e 1)t (C ζ-ζπ-+=2．典型三阶系统在不同开环增益下的响应情况由Routh判据得：S3 1 20S212 20KS10S020K 0要使系统稳定则第一列应均为正数，所以得得0<K<12即R>41.7KΩ时，系统稳定K=12 即R=41.7KΩ时，系统临界稳定K>12即R<41.7KΩ时，系统不稳定二线性系统的根轨迹分析1.绘制图3系统的根轨迹由开环传递函数分母多项式得最高次为3，所以根轨迹条数为3。

实验三 二阶开环系统的频率特性曲线一．实验要求1．研究表征系统稳定程度的相位裕度γ和幅值穿越频率c ω对系统的影响。

2．了解和掌握欠阻尼二阶开环系统中的相位裕度γ和幅值穿越频率c ω的计算。

3．观察和分析欠阻尼二阶开环系统波德图中的相位裕度γ和幅值穿越频率ωc ，与计算值作比对。

二．实验内容及步骤本实验用于观察和分析二阶开环系统的频率特性曲线。

由于Ⅰ型系统含有一个积分环节，它在开环时响应曲线是发散的，因此欲获得其开环频率特性时，还是需构建成闭环系统，测试其闭环频率特性，然后通过公式换算，获得其开环频率特性。

自然频率：TiT K=n ω 阻尼比：KT Ti21=ξ （3-2-1） 谐振频率：221ξωω-=n r 谐振峰值：2121lg20)(ξξω-=r L （3-2-2）计算欠阻尼二阶闭环系统中的幅值穿越频率ωc 、相位裕度γ： 幅值穿越频率： 24241ξξωω-+⨯=n c （3-2-3）相位裕度： 424122arctan)(180ξξξωϕγ++-=+=c（3-2-4）γ值越小，Mp%越大，振荡越厉害；γ值越大，Mp%小，调节时间ts 越长，因此为使二阶闭环系统不致于振荡太厉害及调节时间太长，一般希望：30°≤γ≤70° （3-2-5）本实验所构成的二阶系统符合式（3-2-5）要求。

被测系统模拟电路图的构成如图1所示。

图1 实验电路本实验将数/模转换器（B2）单元作为信号发生器，自动产生的超低频正弦信号的频率从低到高变化（0.5Hz~16Hz ），OUT2输出施加于被测系统的输入端r (t)，然后分别测量被测系统的输出信号的开环对数幅值和相位，数据经相关运算后在虚拟示波器中显示。

实验步骤：（1）将数/模转换器（B2）输出OUT2作为被测系统的输入。

（2）构造模拟电路：安置短路套及测孔联线表同笫3.2.2 节《二阶闭环系统的频率特性曲线测试》。

（3）运行、观察、记录：① 将数/模转换器（B2）输出OUT2作为被测系统的输入，运行LABACT 程序，在界面的自动控制菜单下的线性控制系统的频率响应分析-实验项目，选择二阶系统，就会弹出虚拟示波器的界面，点击开始，实验开始后，实验机将自动产生0.5Hz~16H 等多种频率信号，等待将近十分钟，测试结束后，观察闭环对数幅频、相频曲线和幅相曲线。

实验三 二阶系统的特性测量一、实验目的1、掌握二阶网络的构成方法。

2、掌握二阶网络的系统响应特性。

3、了解二阶网络波特图的测量方法。

二、实验内容1、通过阶跃信号观察其阶跃响应。

2、通过正弦信号观察系统的幅频特性，学会绘制波特图。

三、预备知识了解波特图的绘制。

四、实验仪器1、信号与系统实验箱一台。

2、二阶系统分析模块一块。

3、20MHz 示波器一台。

五、实验原理1、波特图频率特性曲线是实际中用的最多的频率特性形式，而波特图则是描述频率特性曲线的一种很好方式，同时波特图提出用对数坐标绘制波特图的 方法，简化了计算和作图。

下面分析波特图的绘制原理：设系统传函为()()()j H H H e <ΩΩ=Ω 对其两边取自然对数，有()()()()()ln ln H H j H G j H Ω=Ω+∠Ω=Ω+∠Ω⎡⎤⎣⎦式中，()()ln G H Ω=Ω称为对数增益，简称为增益,()H ∠Ω是相位，单位为弧度或度。

工程应用中增益通常用分贝（dB ）为单位表示，此时应对()H Ω取常用对数并乘以20，即()()20lg G H Ω=Ω （dB ）工程应用中，通常将频率坐标用对数尺度表示，称以系统频率响应模的对数和相位大小关于对数频率坐标所作出的频率特性曲线为波特图。

其中 ()G Ω～20lg Ω曲线称为幅度波特图，()H ∠Ω～20lg Ω曲线称为相位波特图。

2、二阶系统在电路系统中，二阶系统是一阶系统的扩展，与一阶系统一样是构成复杂系统基本单元。

一般二阶系统的构成电路如下图：图2-7-1 二阶系统二阶系统的传输函数一般可以写成：2n 2n n()2H s s s 2Ω=+ξΩ+Ω其中n Ω=,ξ=二阶网络的频响函数可以进一步化解为：22212()()2()()n n n b H j j j C j C Ω-Ω==Ω+ξΩΩ+ΩΩ-Ω-1n C =-ξΩ+Ω2n C =-ξΩ-Ω在二阶系统中ξ为二阶系统的阻尼系数，当0＜ξ＜1时系统处于欠阻尼振荡，其单位冲激响应是一个振荡的过程。

二阶系统频率响应咱今儿个来聊聊二阶系统频率响应这事儿。

这听起来有点唬人，其实没那么复杂，就像生活里一些常见的现象背后藏着的小秘密。

二阶系统频率响应啊，简单说就是当有不同频率的信号输入到二阶系统里时，这个系统会给出什么样的反应。

这就好比你去敲不同的鼓，每个鼓都会发出不一样的声音，这声音就是鼓对敲击这个输入信号的一种响应。

想象一下，我小时候家里有个旧收音机。

那个收音机有时候能收到很多台，有时候就只能收到寥寥几个台，这其实就和二阶系统频率响应有点关系。

收音机接收信号就像是一个二阶系统在接收不同频率的输入。

二阶系统的频率响应有一些特性。

它有个自然频率，就像是这个系统自己的一个小节奏。

如果输入信号的频率接近这个自然频率，那这个系统就会变得很兴奋，反应就特别大，就像你在鼓旁边敲出和鼓本身共鸣频率差不多的声音时，鼓发出的声音就特别响亮。

还有阻尼比这个东西。

阻尼比就像是给系统的一种摩擦力。

如果阻尼比小，系统的反应就会像个调皮的小球，在那儿蹦跶很久才停下来。

就像我那个旧收音机，有时候信号不好，声音就会忽大忽小、颤颤悠悠的，就像是阻尼比小的二阶系统在对输入信号做出那种不稳定的响应。

而如果阻尼比合适，系统就会比较平稳地对输入信号做出反应，就像收音机在信号好的时候，声音稳稳当当的。

在实际生活里，很多东西都有二阶系统频率响应的影子。

还是说那个收音机，当我们转动旋钮去调台的时候，其实就是在改变输入信号的频率，然后收音机这个二阶系统就根据不同的频率给出不同的响应，也就是我们听到的不同电台的声音或者嘈杂的声音。

所以啊，二阶系统频率响应虽然听起来是个很专业的东西，但只要联想一下生活中的这些小事情，就会发现它也没那么神秘，就像我们生活中的很多小秘密，只要仔细观察就能发现其中的趣味。

实验二．二、三阶系统动态分析一．实验目的：1．学习二、三阶系统的电模拟方法及参数测试方法；2．观察二、三阶系统的阶跃响应曲线，了解参数变化对动态特性的影响； 3．学习虚拟仪器（超抵频示波器）的使用方法； 4．使用MATLAB 仿真软件进行时域法分析； 5．了解虚拟实验的使用方法。

二．实验设备及仪器1．模拟实验箱； 2．低频信号发生器；3．虚拟仪器(低频示波器)； 4．计算机；5．MATLABL 仿真软件。

三．实验原理及内容实验原理：1、二阶系统的数学模型系统开环传递函数为系统闭环传递函数为2、 二阶系统暂态性能(a) 延迟时间t d : 系统响应从 0 上升到稳态值的 50% 所需的时间。

)2s (s n 2nςω+ω为阻尼比（，为无阻尼自然振荡频率其中：ςωω+ςω+ω==n 2nn 22ns 2s )s (G )s (R )s (C(b) 上升时间t r : 对于欠阻尼系统是指 , 系统响应从 0 上升到稳态值所需的时间 ; 对于过阻尼系统则指 , 响应从稳态值的 10% 上升到 90% 所需的时间。

(c) 峰值时间t p : 系统响应到达第一个峰值所需的时间。

(d) 最大超调量σp ( 简称超调量 ) : 系统在暂态过程中输出响应超过稳态值的最大偏离量。

通常以单位阶跃响应稳态值的百分数来表示 , 即%100e e esin 1e)t sin(1e1)y(t )y()y()y(t σ22pn pn pn 11t 2t p d 2t p p p ⨯===-=+--=-=∞∞-=-------ζπζζπζζωζωζωϕζϕωζ超调量)t sin(1e 1)t (y d 2tn ϕωζζω+--=- 2n d p d 1ωπωπt 0)t sin()t (y ζω-==∴= 峰值时间求导可得对dr t t ωπt 1y(t)rϕ-=== 可令2n21n πϕωξ-=-t ≈n2d n d 2.06.01t 7.01ως+ς+ως+≈或n2d n d2.06.01t 7.01t ως+ς+≈ως+≈或(e) 调节时间t s : 系统响应到达并不再越出稳态值的容许误差带±Δ所需的最短时间 , 即通常取Δ为稳态值的 5% 或 2% 。

二阶系统的瞬态响应一、实验目的1.通过实验了解参数：阻尼比、阻尼自然频率的变化对二阶系统动态性能的影响。

2.掌握二阶系统动态性能的测试方法。

二、实验数据和曲线1. 当阻尼自然频率一定，阻尼比变化时，对二阶系统动态性能影响。

（1）系统处于欠阻尼状态阻尼比 =0.2时，二阶系统的单位阶跃响应曲线：根据实验测量数据可得对应参数如下：调节时间为：0.3184s系统稳态值为：3.071第一次峰值为：4.993超调量=（（第一次峰值-系统稳态值）/系统稳态值）*100%=62.5%（2）系统处于欠阻尼状态，阻尼比ζ=0.707时，二阶系统的单位阶跃响应曲线：根据实验测量数据可得对应参数如下：调节时间为：0.2307s系统稳态值为：3.04第一次峰值为：3.188超调量=（（第一次峰值-系统稳态值）/系统稳态值）*100%=4.8%（3）系统处于临界阻尼状态，阻尼比ζ=1时，二阶系统的单位阶跃响应曲线：根据实验测量数据可得对应参数如下：调节时间为：0.2105s系统稳态值为：3.042处于临界状态，无超调现象发生（4）系统处于过阻尼状态，阻尼比 =2时，二阶系统的单位阶跃响应曲线：根据实验测量数据可得对应参数如下：调节时间为：1.8647s系统稳态值为：3.013过阻尼条件下无超调现象发生。

ω变化时，对二阶系统动态性能影响。

2.当阻尼比一定，nω=1时，二阶系统的单位阶跃响应曲线：（1）系统阻尼自然频率n根据实验测量数据可得对应参数如下：调节时间为：0.9886s系统稳态值为：2.984过阻尼条件下无超调现象发生。

ω=100时，二阶系统的单位阶跃响应曲线：（2）系统阻尼自然频率n根据实验测量数据可得对应参数如下：调节时间为：0.2950s系统稳态值为：3.042第一次峰值为：4.867超调量=（（第一次峰值-系统稳态值）/系统稳态值）*100%=59.9% 三、实验结论。

实验三：二阶系统的频率响应1．实验目的① 学习频率特性的实验测试方法；② 掌握根据频率响应实验结果绘制Bode 图的方法。

2．实验预习要点① 自行设计二阶系统电路。

② 选择好必要的参数值，计算出相应的频率响应数值，预测出所要观察波形的特点，与实验结果比较。

3．实验设备计算机、XMN-2自动控制原理模拟实验箱、CAE-PCI 软件、万用表。

4．实验内容典型二阶系统的方框图和模拟电路图如图3-26所示。

图3-26 典型二阶系统闭环频率特性为：22()1()12n nC j R j j ωωωωξωω=-+闭环传递函数为：222()1,()2n n n n C s R s s s Tωωξωω==++（T 是时间常数）各运算放大器运算功能：OP1，积分，（1,T RC TS -=）； OP2，积分，（1,T RC TS-=）； OP9，反相，（-1）； OP6，反相比例，（3,10010f R k k -=⨯）。

可以得到：11n T RCω== 312210010f R k ξ==⨯ 4. 实验步骤○1 选定R 、C 、f R 的值，使n=1,=0.2ωξ ○2 用Cae98产生r(t)=X sin t ω，使系统得稳态响应为c(t)=C sin( t+ )ωφ; ○3 改变输入信号的频率，使ω的值等于或接近于0.2，0.4，0.6，0.8，1.0，1.2，1.4，1.6，2.0，3.0rad/s ，稳态时分别记录系统得响应曲线，振幅C( )ω和相位( )φω的数据记录于表3-2；表3-2 振幅C( )ω和相位( )φω的数据记录○4 根据表格所整理的数据，在半对数坐标纸上绘制bode 图，标出,r r M ω ○5 根据绘制的bode 图分析二阶系统的%,s t δ ○6 可能的话，改变系统的nω或者ξ，重复上述3-5。

5. 思考题○1 理论计算不同ω和 ( )φω，并和实验结果进行比较。

○2 能否根据所得的bode 图确定二阶系统的传递函数。