探究球面上两点间的最短距离和走法 文档 (2)

两点间最短距离及走法河南濮阳雨打芭蕉在地图与地球的复习中，我们很多老师会遇到“球面上两点间最短距离及走法”问题，下面是我的一点体会。

一、最短距离球面上两点间最短距离不能用平面几何的求法，最基本的原则是“过两点的大圆劣弧段”。

1、此处的大圆我们常见的有三个（类）：赤道、经线圈、晨昏线。

如果两点在这三个圆上则问题就非常简单。

2、如果两点的经度相差不大（在3°以内），可近似看作在同一经线上，最短距离＝纬差×111KM；如果两点的纬度相差不大（在3°以内），可近似看作在同一纬线上，最短距离＝经差×COS纬度×111KM。

3、其他情况属数学问题，地理不作考查。

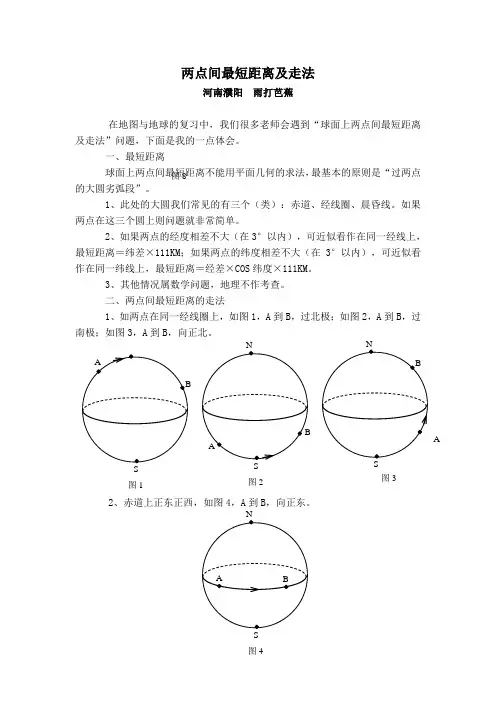
二、两点间最短距离的走法1、如两点在同一经线圈上，如图1，A到B，过北极；如图2，A到B，过南极；如图3，A到B，向正北。

2、赤道上正东正西，如图4，A到B，向正东。

S图4图8AS图3 S图1S图23、如果在晨昏线上，如图5，b 为晨昏线， 从A 到B ，先东北，（再正东），后东南。

4、如图6所示，b 为过A 、B 的大圆，从A 到B ，先东北，（再正东），后东南。

5、如图7所示，b 为过A 、B 的大圆，从A 到B ，先东北，（再正东），后东南。

三、我不同意的一种走法如图8所示，有的资料或老师说“从A 到B ，先东北，（再正东），后东南。

”我不同意。

从数学的角度分析不可能。

10°E90°E°N 图7°N 50°E90°E°N图650°E90°ENb图530°N图8。

精品文档球面上两点间距离的求法球面距离的定义：球上两点和球的球心三点可构成一个平面，称之为大圆，正视这个大圆（从正面看），这两个点之间的弧线长即为球面两点间距离。

球面距离不是指险段的长度而是指的是弧长。

地球表面某点的位置是用纬度和经度来确定的，我们只要知道球面两点的经纬度，就能求出该两点的球面距离。

下面简单的谈谈求法：一. 同经度两点间的球面距离例1. 在地球本初子午线上有两点A 、B 。

它们的纬度差为90°，若地球半径为R ，求A 、B两点间的球面距离。

解：如图1所示，设O 为地球球心，由题意可得，故。

所以：A 、B 两点间的球面距离为2R。

图1二. 同纬度两点间的球面距离例2. 在地球北纬度圈上有两点A、B，它们的经度差为度，若地球半径为R，求A、B两点间的球面距离。

解：设度的纬线圈的圆心为，半径为r，则。

依题意。

取AB的中点C，则。

在图2图3三. 不同纬度、不同经度两点间的球面距离例3. 设地球上两点A、B，其中A位于北纬30°，B位于南纬60°，且A、B两点的经度差为90°，求A、B两点的球面距离。

解：如图4所示，设，分别为地球球心、北纬30°纬线圈的圆心和南纬60°纬线圈的圆心。

图4连结。

则。

由异面直线上两点间的距离公式得下面给出球面距离的计算公式（仅供参考）：设一个球面的半径为，球面上有两点、. 其中，为点的经度数，、为点的纬度数，过、两点的大圆劣弧所对的圆心角为，则有（弧度）A、B间的球面距离为：证明：如图3，⊙与⊙分别为过A、B的纬度圈，过A、C的大圆，过、D的大圆分别为A、B的经度圈，而经度圈与纬度圈所在的平面互相垂直，作面，垂足位于上，连结、. 则在中，由余弦定理，得：故又比较上述两式，化简整理得：过两点的大圆劣弧所对的圆心角为从而可证得关于与的两个式子.例题：北京在东经，北纬，上海在东经，北纬，求北京到上海的球面距离.解：∴（弧度）∴所求球面距离为。

一、球面上最短线路的确定生：球面上有两点A、B，现从A到B走最短线路，怎么走？师：走过AB的球面大圆所在圆弧。

当然走从A到B的劣弧段了。

生：什么是大圆？为什么要走大圆？师：首先我们来假想一个球，然后用刀剖开这个球，剖面应该是一个圆形。

专业述语为“横截面”。

再想一想，怎样剖才能让这个横截面最大呢？生：应该是从球的中心截过去。

师：对，过球心的横截面是最大的。

这个横截面的外圆就是大圆。

生：哦，那大圆长就是球的周长。

师：可以这样说。

不过，一般说圆的周长，不说球的周长。

地球的大圆在哪？生：赤道，经线。

师：赤道是大圆，经线呢只是大圆的一半，应该是两条相对的经线构成的经线圈才能叫大圆。

地球的大圆有多少个？生：这么说来，应该是无数个！师：对。

只要是过球心的平面与球面相交的交线都是大圆。

从A到B的最短线路就是过AB的大圆弧线的一部分。

生：如果AB都在赤道上或经线圈上，那当然就容易找了，因为它们都在同一个大圆上。

如果不在赤道上而在同一条其他纬线上呢？师：其实无论两点在何处，都要先找到过两点的大圆。

我们以下面这幅图为例加以说明：图中A和B在同一纬线上，F和B不在同一经线和纬线上，都ADBF都在同一个大圆上。

所以从图中可以看出，从A到B的最短线路是ADB，而不是ACB。

在右边图中还可以明显看出，ADB的方向发生了明显变化，先往西北到D，过D后往西南到B。

当然，过D点那一瞬为往西。

如果走ACB，则一直往西，但不是最短线路了。

生：为什么大圆就是最短线路呢？师：看看下面这个图。

图中是过a和b的两个圆。

可以明显看出，在ab两点中走大圆的圆弧近些。

圆越大，弧的曲度就越小，线路就越接近直线（因为球面上不可能有直线）。

生：就这个找大圆比较难，很抽象。

有没有更简单的办法呢？师：其实考试中命题者不会在这个地方加深问题的复杂性。

一般掌握这几点足够了：1、两点都在赤道上，晨昏线上或经线圈上，这些明显的大圆弧线可以直接作参考。

2、在同一条纬线而不在赤道上的话，北半球两点的最短线路要从北边绕过，南半球两点的线路要从南边绕过。

探讨球面上【1 】两点间的最短距离和走法在球面上,衔接甲.乙两点有一弦,在同样的弦上,半径最大,所过的弧长最短.过球面上随意率性两点的圆弧都是在某个过这两点的平面与该球切割出的圆上.在球面上,两点间最短距离就是过这两点的大圆（半径等于球体的半径）的劣弧,下图中甲.乙两点,最短距离就是两点地点的经由球心的大圆上的距离.具有地理意义的大圆：经线圈.赤道.晨昏圈（线）（如下图）1.在统一经线圈上的两点（但不在统一条经线上）,过这两点的大圆等于经线圈,过两顶点为两点间最短距离,具体又分为三种情形：A．同位于北半球,比来航程必定是先向北,过顶点后再向南（如图1中的A.B两点）B.同位于南半球,比来航程必定是先向南,过顶点后再向北（如图2中的A.B两点）.C.两地位于南北两个半球,这时须要评论辩论,肯定过哪个顶点的为劣弧,再评论辩论（如图3）2.在晨昏圈上（晨昏线就是经由球心的大圆）A.在晨线上的A.B两点（如图4）,断定较为简略.B.在昏线上的C.D两点（如图5）,断定较为简略.C.分离在晨线和昏线上：从A到D点间比来距离的走法是先向西北再向西南,从B到C点间比来距离的走法是先向东南再向东北（如图6）3.在赤道上的A.B两点正东或正西,最短距离,就是过这两点的大圆的劣弧（图7）4.统一纬线上的两点间最短距离的走法,北半球是先向高纬度,再向低纬度,如图8中的A.B两点,从A到B是先向东北,再向东南.南半球是先向高纬度,再向低纬度,如图8中的C.D两点,从C到D是先向东南,再向东北.5.其他随意率性点间最短距离和偏向的断定两地经度差不等于180,则过两点的大圆不是经线圈,而与经线圈斜交,最短距离不过两顶点,而是过南北极地区（或上空）,可分为两种情形：（1）A地位于B地的西南边,从A到B的最短距离走法为：同在北半球,先向东北再向东南.（如图9）（2）同在南半球,A地位于B地的西方,从A到B的最短距离走法为：先向东南,再向东北.（如图10）（3）位于不合半球时须要评论辩论,办法同上(图11).例1：从甲地(50°N.80°E)到乙地(50°N.160°E)若不斟酌地形身分,比来走法是A．一向向正东偏向走B．先向东南再向东最后向东北走C．先向东北再向东最后向东南走D．先向东南再向东北走例2：从华盛顿到北京在以下四条航路中,最短的一条是：A 华盛顿—夏威夷—北京B 华盛顿—悉尼—北京C 华盛顿—阿拉斯加—北京D 华盛顿—开罗—北京例3.图中ACB为晨昏线, C地点在格陵兰岛上.那么从A到B比来的走法是A 沿北纬30度向东到达BB 沿弧线ADB走到BC 沿弧线ACB走到BD 无法断定。

球面最短距离一、概述球面最短距离是指在一个球体上两点之间的最短路径，也称为大圆弧距离或者地球表面的测地线。

在地理学、天文学、航空航天等领域中，球面最短距离是一个十分重要的概念。

二、公式推导假设有两个球面上的点A和B，它们的经纬度分别为(φ1, λ1)和(φ2,λ2)，其中φ表示纬度，λ表示经度。

则它们之间的大圆弧距离d可以通过以下公式计算：d = R * arccos(sinφ1 * sinφ2 + cosφ1 * cosφ2 * cos(λ1 - λ2))其中R为球体半径。

这个公式可以通过余弦定理推导得到。

将球体看作一个半径为R的圆，以A点和B点为圆心画出两条半径，并连接这两个点。

则这两个半径与圆周所夹成的角就是AB之间的大圆弧角度θ。

根据余弦定理，我们可以得到：cosθ = cosR / (cosA * cosB) - tanA * tanB / (cosA * cosB)其中A和B分别为AB连线与北极点连线所成角度，R为球体半径。

将A和B带入上式可以得到：cosθ = sinφ1 * sinφ2 + cosφ1 * cosφ2 * cos(λ1 - λ2)因为θ就是AB之间的大圆弧角度，所以d可以表示为：d = R * θ将θ带入上式即可得到球面最短距离公式。

三、应用场景1. 地理学：在地球表面上，球面最短距离可以用来计算两个城市之间的距离。

这个概念在航空、航海、旅游等领域中都有广泛的应用。

2. 天文学：在天文学中，球面最短距离可以用来计算星际之间的距离。

例如，在太阳系内，我们可以使用这个概念来计算地球和其他行星之间的距离。

3. 机器人领域：在机器人领域中，球面最短距离可以用来规划机器人移动路径。

例如，在一个球形空间中，机器人需要从一个点移动到另一个点，我们就可以使用这个概念来计算机器人需要走多长的路程。

四、误差分析虽然球面最短距离公式非常有用，但是它并不是完全准确的。

这是因为地球并不是一个完美的球体，而是一个略微扁平的椭球体。

地球表面上两点间最短距离（航线）方向的确定作者：***来源：《中学政史地·高中文综》2016年第03期在复习经纬网的内容时，地球表面上两点间最短航线方向的确定，是我们的拦路虎。

由于有的同学对这类问题缺乏足够的空间想象能力，只是机械地背一些结论，造成在解这类试题时经常出错。

针对有些同学空间想象能力和数学水平不太高等情况，本文旨在帮助他们全面正确认识地球表面上两点间最短航线方向的确定问题。

地球表面上两点之间的最短航线，指的是两点所在大圆的劣弧。

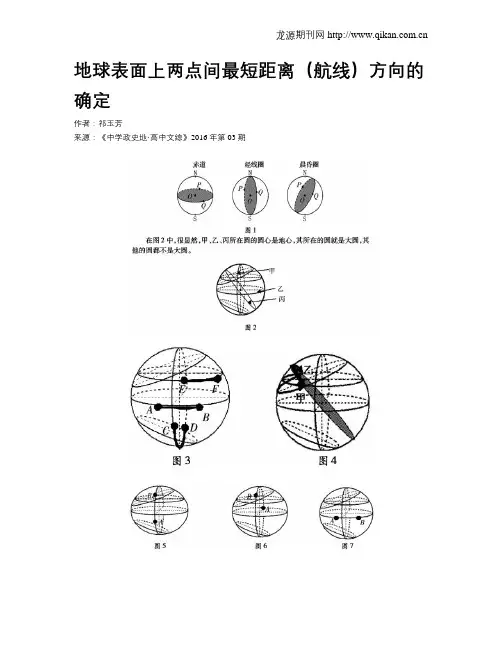
一、认识大圆过球面上两点的大圆就是经过这两点以地心为圆心的圆。

在地球上有三种情况大圆是确定的，如图1中的赤道、经线圈、晨昏圈。

在图2中，很显然，甲、乙、丙所在圆的圆心是地心，其所在的圆就是大圆，其他的圆都不是大圆。

二、确定劣弧大圆上两点间的最短航线或距离就是两点所在大圆的劣弧。

所谓劣弧，即两点间的弧度小于180°。

如图3中的⌒AB和⌒CD都是过大圆的劣弧，而⌒EF虽然是劣弧，但不是大圆上的劣弧。

图4中甲和乙之间的弧线，只有最上面的弧是过大圆的劣弧。

三、确定地球上两点间最短航线的方向沿着劣弧的行进方向就是最短航线的方向。

1.两点在同一经线圈上或者在赤道上（1）两点在同一经线上，向正北或向正南走，不转向。

如图5， A到B是向正北走；反之，B到A是向正南走。

（2）两点在两条经线上（经度相对，两点的经度差等于180°），过极点要转向。

如在通过北极点之前，先向正北走，过北极点后转向正南；反之，在通过南极点之前，先向正南走，过南极点后转向正北。

如图6，从A到B先向正北走，过北极点后向正南走；从B 到A是先向正北走，过北极点后向正南走。

（3）两点在赤道上，向正东走或向正西走，不转向。

如图7， A到B是向正东走；反之，B到A是向正西走。

2.两点既不在同一经线上，也不在赤道上地球上任意两点和地心必然确定一个大圆，一定存在一个纬线圈和这个大圆相切，切点即为这个大圆的纬度最高点，若大圆劣弧航线经过切点，则发生转向，转向点为切点；若大圆劣弧航线不经过切点，则不发生转向。